1. Введение

Меня всегда удивляет «менталитет» представителей славянской (российской, украинской, белорусской) науки. В течение нескольких столетий повторяется одна и та же история – любыми способами принизить научные достижения своих собственных, славянских талантов, довести их до инфаркта, унизительной старости или гибели и только после их смерти вдруг начать вспоминать, какими же гениальными они были. Так было с Николаем Лобачевским, которого официальная академическая наука России в свое время подвергла осмеянию. Гениальный геометр умер непризнанным в своей стране, хотя благодаря Гауссу за рубежом он был признан при жизни. Так же было с гениальным химиком Дмитрием Менделеевым, который в свое время не был избран академиком Российской академии наук. Кто сейчас помнит тех «академиков», которые проголосовали против Менделеева? А Менделеева помнят все. А дальше еще страшнее. Достаточно вспомнить судьбу таких российских гениев, как Алексей Лосев, Павел Флоренский, Николай Вавилов и др. Много ли в Российской академии академиков, которых можно сравнить с Лосевым, Флоренским или Вавиловым? То есть, оказывается, академиков много, а настоящих ученых – не очень. Известно, что украинская наука за все годы своего существования не взрастила в своих рядах ни одного Лауреата Нобелевской Премии (!). В то же время много выходцев из Украины за рубежом почему-то стали Лауреатами Нобелевской Премии (Абрахам Ваксман, уроженец Винниччины, Илья Мечников, Шмуэль Агнон, Семен Кузнецов, Роальд Гофман, Георгий Шарпак). А сколько представителей Беларуси стали Лауреатами Нобелевской Премии? Почему складывается такая ситуация? Славяне что – глупее других наций? Наверное, все дело в отношении к талантам. И если мы хотим, чтобы славянская наука достойно была представлена в мировом научном сообществе, необходимо радикально менять отношение к талантливым ученым и изменять правила избрания ученых в Академии Наук. Академиками должны становиться настоящие ученые, а не научные администраторы, государственные и политические деятели!

В этой статье мне хотелось бы рассказать о научных исследованиях одного из талантливых славянских ученых, белорусского философа Эдуарда Сороко, научные достижения которого вполне заслуживают того, чтобы быть представлеными на соискание Нобелевской Премии от Республики Беларусь.

С Эдуардом Максимовичем Сороко меня связывает многолетнее творческое содружество. Он неоднократно приезжал ко мне в гости в Винницу и его блестящие лекции для студентов и преподавателей Винницкого политехнического института, где я заведовал кафедрой вычислительной техники, всегда становились большим научным праздником. Однако после публикации его книги «Структурная гармония систем» (1984) мой интерес к его исследованиям особенно возрос. Причиной стало то обстоятельство, что каждый из нас независимо друг от друга пришел к одному и тому же фундаментальному математическому результату – так называемым обобщенным золотым пропорциям. Но пути, которые привели нас к этому научному открытию, были разными. Сороко пришел к этому результату с весьма общих, философских позиций, исследуя так называемое «уравнение диалектического противоречия», что и привело его к формулировке всеобщего философского закона, который он назвал «Законом структурной гармонии систем» [1]. Я же пришел к обобщенным золотым пропорциям, решая сугубо прикладную задачу в области алгоритмов аналого-цифрового преобразования, которая и легли в основу моей первой математической теории, названной мною алгоритмической теорией измерения [2, 3, 4]. В дальнейшем я использовал обобщенные золотые пропорции для введения так называемых кодов золотой пропорции [5], а еще позже – для развития так называемой Математики Гармонии [6-10], нового междисциплинарного направления современной науки, которое касается оснований математики и компьютерной науки. Естественно, что мои прикладные научные теории и результаты являлись своеобразным подтверждением всеобщего «Закона структурной гармонии систем», сформулированного Э.М. Сороко», который всегда внимательно следил за развитием моего научного направления. Вообще весьма удивительно, что одно и то же математическое понятие – обобщенные золотые пропорции – было положено как в основу «Закона структурной гармонии систем» (Сороко), так и в основу «Математики Гармонии» (Стахов). И я хотел бы начать рассмотрение вклада Э.М. Сороко в развитие общей теории Гармонии и Золотого Сечения с обсуждения обобщенных золотых пропорций – фундаментального математического результата современной науки.

2. Как я пришел к р-числам Фибоначчи и золотым р-пропорциям?

Я начал свою научную деятельность в период своей учебы в аспирантуре Харьковского института радиоэлектроники (1963-1966). Темой моих исследований были аналого-цифровые и цифроаналоговые преобразователи. Одним из направлений моих исследований стали «оптимальные алгоритмы» аналого-цифрового преобразования. Своими идеями я сумел заинтересовать талантливого математика Игоря Витенько, выпускника Львовского университета, который в это период работал преподавателем ХИРЭ. Именно с Витенько нам удалось открыть новый класс алгоритмов аналого-цифрового преобразования, названных «фибоначчиевыми» алгоритмами. Эти алгоритмы основывались на интересных числовых последовательностях, названных р-числами Фибоначчи. При заданном целом р=0, 1, 2, 3,... эти числовые последовательности задавались следующей рекуррентной формулой:

Fp(n+1) = Fp(n)+Fp(n-p)

(1)

при следующих начальных условиях:

Fp(1) = Fp(2) =... = Fp(p+1) = 1

(2)

Оказывается, что при различных значениях р рекуррентная формула (1) при начальных условиях (2) «генерирует» бесконечное число числовых последовательностей. При р=0 это будет широко известный нам «двоичный» ряд чисел: 1, 2, 4, 8, 16,.... А вот при р=1 рекуррентная формула (1) при начальных условиях (2) «генерирует» знаменитый «ряд Фибоначчи»: 1, 1, 2, 3, 5, 8, 13, 21,..., открытый еще в 13-м веке известным итальянским математиком Леонардо из Пизы (по прозвищу Фибоначчи).

Когда же нам с Витенько удалось открыть «фибоначчиевые» алгоритмы измерения? Первая наша публикация на эту тему [11] относится к 1966 г. На основе этой небольшой публикации (тезисы докладов) мною с Витенько была написана большая статья [12], опубликованная в 1970 г. Именно статьи [11, 12] и являются подтверждением нашего с Витенько приоритета в открытии «фибоначчиевых» алгоритмов измерения, основанных на р-числах Фибоначчи (1), (2).

В 1971 г. наши жизненные (но не научные) пути с Игорем Витенько разошлись. Он переехал в Ужгород, где стал работать доцентом кафедры математической логики Ужгородского университета, а я уехал в Таганрог, где стал работать зав. кафедрой информационно-измерительной техники Таганрогского радиотехнического института. И до 1974 г. мы с Игорем Витенько поддерживали тесные творческие контакты и активно переписывались. В 1974 г. случилось трагическое событие в истории украинской науки – Игорь Витенько покончил жизнь самоубийством. Ценой своей жизни Игорь Витенько выразил протест против Ужгородского обкома КПСС и парткома Ужгородского университета, которые начали его травить за то, что его отец и мать были «бандеровцами». Более детально о трагической судьбе Игоря Витенько я рассказал в автобиографической книге «Под знаком Золотого Сечения: Исповедь сына студбатовца»

http://www.trinitas.ru/rus/doc/0232/100a/02320012.htm

Начиная с 1974 г. мое научное направление (коды и арифметика Фибоначчи, коды золотой пропорции и др.) развивались без участия Игоря Витенько. В 1977 г. издательство «Советское Радио» (Москва) опубликовало мою книгу «Введение в алгоритмическую теорию измерения» [2], которая была посвящена светлой памяти Игоря Витенько.

В процессе написания этой книги я обнаружил, что независимо от меня к обобщенным числам Фибоначчи пришли американские математики-фибоначчисты [13-16]. Однако их путь к р-числам Фибоначчи был другим. Они начали исследовать так называемые «диагональные суммы» треугольника Паскаля [15]. Меня этот подход заинтересовал. И я использовал этот подход при исследовании математических свойств р-чисел Фибоначчи, введенных мною с Витенько еще в 1966 г. Связь р-чисел Фибоначчи с треугольником Паскаля настолько интересна, что я позволю себе повторить те рассуждения, которые я провел еще в 1977 г. в книге [2].

Расположим биномиальные коэффициенты в виде следующей таблицы, которую называют прямоугольным треугольником Паскаля.

Прямоугольный треугольник Паскаля

Если просуммировать теперь биномиальные коэффициенты n-го столбца рассматриваемого треугольника Паскаля, то мы получим «двоичное число» 2ⁿ. Если это сделать для всех столбцов, начиная с нулевого, то мы получим широко известный нам «двоичный ряд чисел»: 1, 2, 4, 8, 16, 32, 64, …., 2ⁿ, …. Таким образом, мы можем утверждать, что треугольник Паскаля «генерирует» двоичный ряд чисел!

А теперь сдвинем каждый ряд исходного треугольника Паскаля на один столбец вправо относительно предыдущего ряда. В результате такого преобразования мы получим некоторый «деформированный» треугольник Паскаля, который мы будем называть 1-треугольником Паскаля.

1-треугольник Паскаля

Если теперь просуммировать биномиальные коэффициенты 1-треугольника Паскаля по столбцам, то, к нашему изумлению, мы обнаружим, что такое суммирование приведет нас к числам Фибоначчи: 1, 1, 2, 3, 5, 8, 13, ….

А теперь «закрепим наш успех»! Если теперь в исходном треугольнике Паскаля сдвинуть биномиальные коэффициенты каждого ряда на р=2 столбца вправо относительно предыдущего ряда, то мы получим новый «деформированный» треугольник Паскаля, который мы назовем 2-треугольником Паскаля.

2-треугольник Паскаля

Если теперь просуммировать биномиальные коэффициенты по столбцам, то мы получим следующий числовой ряд: 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60,....

А теперь рассмотрим ситуацию, когда в исходном треугольнике Паскаля мы сдвигаем биномиальные коэффициенты каждого ряда на р столбцов вправо относительно предыдущего ряда, где р может принимать значения из множества {0, 1, 2, 3,... }. Полученный таким путем «деформированный» треугольник Паскаля мы будем называть р-треугольником Паскаля.

Нетрудно показать (или догадаться), что суммирование биномиальных коэффициентов р-треугольника Паскаля приведет нас к некоторому новому числовому ряду, который в общем виде задается рекуррентным соотношением (1) при начальных условиях (2).

В книге [2] мне удалось вывести общую формулу, которая связывает р-числа Фибоначчи с биномиальными коэффициентами:

(3)

Подобной формулы в работах американских математиков-фибоначчистов я не встречал. По-видимому, они прошли мимо этого результата.

Заметим, что при р=0 р-числа Фибоначчи сводятся к «двоичным» числам, а формула (3) принимает вид следующей формулы, хорошо известной в комбинаторном анализе:

+ + … + = 2n.

(4)

Но оказывается математики-фибоначчисты не были первыми, кто обнаружил связь чисел Фибоначчи с треугольником Паскаля. В 1970 г. на русский язык была переведена книга выдающегося математика и педагога Д.Пойа «Математическое открытие» [17] (на английском языке книга издана в 1962 г.). В этой книге на с. 113-114 приводятся упражнения с треугольником Паскаля, из которого вытекает связь чисел Фибоначчи с треугольником Паскаля. Кроме того, к этому же пришли позже известные математики Гарднер и Ренье. Таким образом, обнаружение связи чисел Фибоначчи с Треугольником Паскаля было сделано многими математиками независимо друг от друга и практически одновременно. Такое в науке встречается очень часто. И такое одновременное появление одного и того же научного результата в работах многих ученых возникает всегда, когда наука «созревает» для этого научного открытия. С моей точки зрения, установление связи чисел Фибоначчи с треугольником Паскаля и открытие обобщенных чисел Фибоначчи, к чему пришли многие математики практически одновременно, можно считать одним из важных математических открытий 20-го века!

Еще раз хочу подчеркнуть, что к р-числам Фибоначчи мы с Витенько пришли в 1966 г. [12] при решении задачи синтеза «фибоначчиевого» алгоритма измерения, то есть без какой-либо связи с треугольником Паскаля. А обнаруженная многими математиками связь р-чисел Фибоначчи с треугольником Паскаля только подчеркивает их фундаментальный характер.

Почему я об этом так подробно рассказываю? Дело в том, что в сочинениях некоторых «новых русских» подвергается сомнению мой приоритет в р-числах Фибоначчи. При этом мои оппоненты пытаются противопоставить мне работы Пойа, Гарднера и Ренье. Но ведь в работах этих прославленных математиков мы не найдем рекуррентной формулы (1), сколько бы мы не искали. В работе Пойа [17] намечен путь, который может привести нас к р-числам Фибоначчи. Но формул (1) и (3) там не выведено. Скорее всего, нам с Витенько можно противопоставить работы математиков-фибоначчистов [13-16]. Но при этом ни в коей степени нельзя отрицать наш с Витенько приоритет в открытии «фибоначчивых» алгоритмов измерения, основанных на рекуррентном соотношении (1).

Теперь еще об одном моем математическом открытии, полученном на раннем этапе моего научного творчества и описанном в книге [2]. Речь идет об обобщенных золотых пропорциях или золотых р-пропорциях. Я рассуждал следующим образом. Как известно, отношение соседних чисел Фибоначчи:

(5)

в пределе стремится к золотой пропорции, то есть

(6)

Считается, что связь чисел Фибоначчи с Золотой Пропорцией первым обнаружил Иоганн Кеплер.

Естественно, я поставил вопрос: к чему стремится отношение соседних р-чисел Фибоначчи? В книге [2] мне удалось доказать, что в общем случае (для заданного целого р=0, 1, 2, 3,...) отношение соседних р-чисел Фибоначчи F_p(n)/F_p(n-1) стремится к некоторому постоянному числу t _р, которое является положительным корнем следующего алгебраического уравнения:

xр+1 = xр + 1.

(7)

Положительный корень этого уравнения t _р я назвал в [2] обобщенной золотой пропорцией или золотой р-пропорцией.

Мне приятно, что в последние годы некоторые исследователи в области «теории Золотого Сечения» называют уравнение (7) моим именем. Это уравнение, действительно, обладает интересными математическими свойствами, что показано в работах [18, 19].

В книге [2] мне удалось также строго геометрически сформулировать «задачу о золотом р-сечении отрезка». Ее суть сводится к следующему. Как известно, «золотое сечение» отрезка АВ точкой С представляет собой его деление на две неравные части АС и СВ так, чтобы выполнялась следующая пропорция:

(8)

Эта задача допускает следующее обобщение [2]. Зададимся целым неотрицательным числом р=0, 1, 2, 3,... и разделим отрезок AВ точкой C в следующей пропорции:

(9)

Если обозначить и учесть, что АВ = АС + СВ, то отношение можно представить в виде:

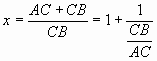(10)

Учитывая введенное выше обозначение и пропорцию (9), выражение (10) можно записать в виде:

,

откуда непосредственно вытекает алгебраическое уравнение (7).

Это означает, что деление отрезка в отношении (9) является делением отрезка в золотой р-пропорции t _р.

Заметим, что пропорция (9) сводится к «дихотомии» (то есть к делению отрезка пополам) для случая p = 0 и к классическому золотому сечению для случая p = 1. Учитывая это обстоятельство, деление отрезка AB точкой C в пропорции (9) было названо в [2] золотым p-сечением.

Подведем некоторые итоги. Из проведенного исследования вытекает, что треугольник Паскаля, который нам известен, по крайней мере, с 17-го столетия, хранит много интересных тайн, одну из которых удалось раскрыть только во второй половине 20-го века, благодаря исследованиям Пойа, Гарднера, Ренье, американских математиков-фибоначчистов, а также моим исследованиям. Суть этого открытия состоит в том, что треугольник Паскаля «генерирует» бесконечное число новых рекуррентных числовых последовательностей, которые названы р-числами Фибоначчи. Кроме того, исследование р-чисел Фибоначчи, проведенное мною в книге [2], привело к открытию нового класса иррациональных чисел t _р, которые я назвал золотыми р-пропорциями. С увеличением р золотая р-пропорция становится все меньше и в предельном случае (р® Ґ) t _р ® 1.

В таблице приведены значения золотых р-пропорций для некоторых значений р.

Золотые р-пропорции

Таким образом, между числами 2 и 1 находится бесконечное число новых иррациональных чисел, золотых р-пропорций, которые, с одной стороны, выражают некоторые неизвестные нам ранее свойства треугольника Паскаля, а с другой — более сложные «гармонии», чем классическая золотая пропорция t = 1,618. То есть, золотых пропорций существует бесконечное количество.

Сейчас некоторые «новые русские», не отрицая моего приоритета в открытии золотых р-пропорций, пытаются всячески принизить это мое открытие, ссылаясь на то, что сам вывод уравнения (7) очень прост (какое ж это открытие?). На это замечание я хотел бы ответить следующим образом. Действительно, вывод уравнения (7) очень прост и его может сделать любой студент. Вопрос только в том, кто первым вывел это уравнение. Здесь уместно вспомнить исследование отношения диагонали к стороне квадрата, которое привело пифагорейцев к открытию «несоизмеримых отрезков», одному из важнейших открытий античной математики. Доказательство существования «несоизмеримых отрезков» настолько простое, что его может сегодня повторить любой школьник. Это, однако, не умаляет вклада пифагорейцев, потому что они первыми пришли к этому открытию.

В дальнейшем р-числа Фибоначчи и золотые р-пропорции были использованы мною для развития следующих прикладных математических теорий:

1. Разработка нового направления в теории измерения, названного алгоритмической теорией измерения [2-4].

2. Разработка общей теории систем счисления с иррациональными основаниями, названных мною кодами золотой пропорции [5].

3. Разработка новых компьютерных арифметик и вытекающей из них «теории компьютеров Фибоначчи» [2, 5]. Это научное направление защищено 65 патентами США, Японии, Англии, Франции, Германии, Канады и др. стран.

4. Разработка троичной зеркально-симметричной арифметики [20].

5. Разработка нового подхода к геометрическому определению понятия действительного числа и вытекающей из него новой теории действительных чисел, основанной на золотых р-пропорциях [21].

6. Обобщение «формул Бине» [19].

7. Открытие обобщенных чисел Люка, названных р-числами Люка [19].

8. Открытие нового свойства натуральных чисел, названного Z-свойством [21].

9. Открытие нового класса гиперболических функций, названных гиперболическими функциями Фибоначчи и Люка [22, 23].

10. Разработка теории «матриц Фибоначчи» и вытекающей из них новой теория избыточного кодирования [24].

11. Разработка теории «золотых» матриц и вытекающего из них нового метода криптографии [9].

Совокупность всех этих математических результатов я назвал «Математикой Гармонии» в докладе, который я сделал на 7-й Международной конференции по числам Фибоначчи и их приложениям (Австрия, Грац, 1996) [6]. Можно спорить или иронизировать по поводу моего научного направления, но опровергнуть его невозможно. Это не под силу «новым русским», которые не обладают для этого соответствующими математическими знаниями. Для меня в данном случае имеет значение только мнение крупных ученых, одним из которых является выдающийся математик, академик Юрий Митропольский, отзыв которого на мое научное направление размещен на Интернете

http://www.trinitas.ru/rus/doc/0232/006a/02320005.htm.

3. Учение о Гармонии в своем историческом развитии
(от Пифагора до Сороко)

Чтобы понять значение открытия Эдуарда Сороко [1] для дальнейшего развития науки, необходимо рассмотреть Учение о гармонии в его историческом развитии.

Пифагорейское учение о числовой гармонии Мироздания

Пифагорейцы впервые выдвинули мысль о гармоническом устройстве всего мира, включая сюда не только природу и человека, но и весь космос. Согласно пифагорейцам, «гармония представляет собою внутреннюю связь вещей, без которой космос не смог бы существовать». Наконец, согласно Пифагору гармония имеет численное выражение, то есть, она интегрально связана с концепцией числа. Пифагорейцы создали учение о созидательной сущности числа. Аристотель в «Метафизике» отмечет именно эту особенность пифагорейского учения: «Так называемые пифагорейцы, занявшись математическим науками, впервые двинули их вперед и, воспитавшись на них, стали считать их началами всех вещей... Так как, следовательно, все остальное явным образом уподоблялось числам по всему своему существу, а числа занимали первое место во всей природе, элементы чисел они предположили элементами всех вещей и всю вселенную [признали] гармонией и числом».

Пифагорейцы признавали, что форма мира должна быть гармонической, а все элементы мироздания («стихии») связаны с гармоническими фигурами. Пифагор учил, что из куба возникла земля, из пирамиды (тетраэдра) – огонь, из октаэдра – воздух, из икосаэдра – вода, из додекаэдра – сфера вселенной (то есть эфир).

С таким представлением о гармонии связано и знаменитое пифагорейское учение о «гармонии сфер». Пифагор и его последователи считали, что движение светил вокруг центрального мирового огня создает чудесную музыку, воспринимаемую не слухом, а разумом. Учение о «гармонии сфер», о единстве микро- и макрокосмоса, учение о пропорциях – все эти идеи и составляют основу пифагорейского учения.

Главный вывод, который вытекает из пифагорейского учения, состоит в том, что гармония объективна, она существует независимо от нашего сознания и выражается в гармоничном устройстве всего сущего, начиная с космоса и заканчивая микромиром.

Последователи Пифагора

Платон. Пифагорейское учение о числовой гармонии мироздания оказало огромное влияние на развитие всех последующих учений о природе и сущности гармонии и получило отражение и развитие в работах великих мыслителей, в частности, оно лежит в основе космологии Платона. В своих работах Платон развивает пифагорейское учение, особенно подчеркивая космическое значение гармонии. Он твердо убежден в том, что мировую гармонию можно выразить в числовых пропорциях. Влияние пифагорейцев особенно прослеживается в «Тимее», где Платон вслед за пифагорейцами развивает учение о пропорциях и анализирует роль правильных многогранников («Платоновых тел»), из которых, по его мнению, Бог создал мир.

Птоломей. Клавдий Птоломей рассматривает гармонию как логическое начало, которое является предпосылкой простоты, всеобщности и порядка. По его мнению, к изучению гармонии следует подходить не с помощью слуха, а с помощью науки и прежде всего математики. По мнению Эдуарда Сороко, Птоломей был первым, кто ввел понятие «Золотого Сечения».

Августин. В средние века пифагорейское учение получает дальнейшее развитие в сочинениях одного из видных «отцов церкви» Аврелия Августина (354-430). Согласно Августину всякая красота основана на пропорции и соответствии. Предметы прекрасны, когда «части их взаимно друг другу подобны и благодаря своему соединению составляют гармонию». Однако все эти части соотносятся друг к другу не произвольно, они основаны на порядке, числе и единстве. Согласно Августину, именно число есть основа красоты, которую мы воспринимаем посредством слуха и зрения.

Боэций. Средневековое представление о гармонии получило наибольшее отражение в трактатах, посвященных музыке. В средние века сам термин «музыка» означал нечто иное, чем в наше время. Он обозначал, прежде всего, одну из теоретических дисциплин в системе средневекового образования, которая стояла в одном ряду с арифметикой, астрономией и геометрией. Предметом этой дисциплины были не столько музыкальное искусство, сколько те математические пропорции и соотношения, которые лежат в основе музыки. В средние века считалось, что законы мира являются в своей основе музыкальными законами. Наиболее ярким представителем подобной точки зрения является средневековый философ Боэций (480-525). Начиная с Боэция, в эстетику средневековья прочно вошло учение о трех видах музыки: мировой (mundana), человеческой (humana) и инструментальной (instrumentalis). Фактически в представлении о мировой музыке Боэций реализовал пифагорейское учение о мировой гармонии. В современной науке подобные идеи развиваются в работах российского исследователя доктора философских наук, профессора Александра Волошинова, написавшего прекрасную книгу на эту тему «Математика и искусство» [25].

Эпоха Возрождения. В эпоху Возрождения, начиная с 15 в., формируется новое понимание мира и личности человека, который ставится в центр мироздания («гармонический человек»). В трудах великих гуманистов этой эпохи Джованни пико дела Мирандоллы (1463-1494), Леона Батиста Альберти (1404–1472) учение о гармонии получает дальнейшее развитие. Широко известно следующее высказывание Альберти о гармонии:

«Есть нечто большее, слагающееся из сочетания и связи трех вещей (числа, ограничения и размещения), нечто, чем чудесно озаряется весь лик красоты. Это мы называем гармонией, которая, без сомнения, источник всякой прелести и красоты. Ведь назначение и цель гармонии – упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту … И не столько во всем теле в целом или в его частях живет гармония, сколько в самой себе и в своей природе, так что я назвал бы ее сопричастницей души и разума. И есть для нее обширнейшее поле, где она может проявиться и расцвести: она охватывает всю жизнь человеческую, пронизывает всю природу вещей. Ибо все, что производит природа, все это соизмеряется законом гармонии. И нет у природы большей заботы, чем та, чтобы произведенное ею было совершенным. Этого никак не достичь без гармонии, ибо без нее распадается высшее согласие частей».

Анализируя это высказывание Альберти, известный исследователь Гармонии В.П. Шестаков [26] выделяет ряд важных моментов в этом высказывании. Самым главным из них является следующее:

«Гармония является законом не только искусства, но и природы, она охватывает всю жизнь человека и всю природу вещей. Гармония в искусстве является отражением гармонии в природе. Наилучшей моделью для нее является гармония частей живого организма, которая лучше всего воплощает в себе согласие и соответствие частей».

В эпоху Возрождения продолжаются поиски «совершенной пропорции». В работах Леонардо да Винчи и Дюрера учение о пропорциях сводится к поискам идеальной меры человеческого тела («Витрувийский человек» Леонардо да Винчи). В этот период возрождается интерес к «золотому сечению», а Леонардо да Винчи (вслед за Птоломеем) по мнению многих исследователей вводит это название в широкое употребление. Под непосредственным влиянием Леонардо в эту эпоху издается одно из самых знаменитых сочинений о «Золотом Сечении». Речь идет о трактате известного итальянского математика Луки Пачоли «О божественной пропорции». Пачоли не случайно вводит в название своего трактата термин «божественный». Он совершенно убежден в божественном происхождении «Золотой Пропорции».

«Гармония мира» Иоганна Кеплера. Среди крупных ученых 17-го столетия, уделявших много внимания проблемам гармонии, прежде всего, необходимо выделить гениального астронома Иоганна Кеплера (1571-1630). Наибольшую популярность приобрел его трактат «Гармония мира» (1619). В этом сочинении Кеплер дает яркую картину гармонического устройства Вселенной. Как подчеркивает Шестаков [26], «основная идея трактата Кеплера состоит в том, что гармония представляет собой универсальный мировой закон. Она придает целостность и закономерность устройства Вселенной. Этому закону подчинено все – и музыка, и свет звезд, и познание, и движение планет».

Пифагорейское учение о «музыке сфер» получает у Кеплера дальнейшее развитие Согласно Кеплеру, шесть планет, вращающихся вокруг Солнца, образуют между собой отношения, которые выражаются гармонической пропорцией. Каждая планета соответствует определенному музыкальному ладу и определенным тембрам голоса. Так, Сатурн и Юпитер, по его мнению, обладают свойством баса, Марс – тенора, Земля и Венера – альта, Меркурий – дисканта.

Кеплеру принадлежат следующие замечательные слова: «В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем». Напомним, что старинная задача о делении отрезка в крайнем и среднем отношении, о которой упоминается в этом высказывании, – это и есть Золотое Сечение!

Учение Лейбница о «предустановленной гармонии». Лейбницу принадлежит знаменитое учение о «предустановленной гармонии», которое было частью его философской системы и имело теологическую окраску. Лейбниц рассматривает гармонию как универсальный закон связи и красоты Вселенной. Лейбниц представлял гармонию, как некоторое состояние, предопределенное Богом. Свое отношение к гармонии он выразил в следующих словах: «Преднамеренное устроение планет и животных более чем что-либо подтверждает мою систему предустановленной гармонии». Этой же точки зрения придерживался и великий Ньютон. Как пишет известный физик Л. Розенфельд, Ньютон свято верил в то, что «регулярность явлений природы не может быть делом случая, в ней проявляется наличие верховной мудрости и верховного интеллекта, которые все задумали в соответствии со своим назначением и великой гармонии всего творения» (цитата взята из [26]).

«Мировая гармония» Шефтсбери. Одна из грандиозных космологических концепций гармонии принадлежит английскому философу и эстетику Шефтсбери (1671-1713). Согласно Шефтсбери, «гармония царит во всем мире, она является упорядочивающим и творческим началом всей природы и космоса». Одним из центральных понятий философии и эстетики Шефтсбери является понятие целого, оно означает универсальную связь и единство явлений и вещей. Вся природа – это целесообразно и гармонично устроенное целое. И в природе и в искусстве отдельные вещи и явления существуют как часть целого, как момент в общей системе красоты и гармонии.

Учение Гегеля о гармонии и мере. В работах великого немецкого философа Гегеля (1770 — 1831) содержится подробное систематическое учение о гармонии. Он развивает математическое представление о гармонии, рассматривая ее в системе других эстетических категорий, таких, как правильность, симметрия, закономерность.

«Учение о ноосфере» В.И. Вернадского. По широте научного кругозора и разнообразию научных открытий Владимир Иванович Вернадский стоит, пожалуй, особняком среди других великих естествоиспытателей 20-го столетия. Молекулярные кристаллические структуры, планетарные геохимические оболочки, история минералов и геосфер, движение химических элементов Земли, геологическая роль «живого вещества» в истории планеты, учение о ноосфере — таков в кратком перечислении круг научных интересов ученого-мыслителя, идеи которого приобретают со временем все большую актуальность. За последние сто лет науки преимущественно обособлялись, дробились, рождались. Вернадский, как мы знаем, не считался с границами отдельных наук, объединял различные области знания (геохимию с биологией, геологию с экономикой, историю науки с естествознанием и т. д.). Проводя специальные научные исследования, он был в то же время философом, историком, организатором науки, касался проблем морали, человеческой личности, свободы и справедливости. Как подчеркивает Олег Боднар в своей статье [27], «сравнительно недавно – в начале ХХ столетия, В.И.Вернадским была выдвинута великая идея – идея ноосферы. Ее глубина и важность начинает осознаваться только сегодня, когда человечество стало ощущать опасность глобальной катастрофы. И это не преувеличение. Идея философии ноосферы, предложенная В.И.Вернадским, не что иное, как идея нового мировоззрения, лишь поворот к которой в начале ХХІ века даст человечеству шанс на продолжение жизни, развитие ее в направлении разумного взаимодействия с природой. Идея гармонии, по мнению современных апологетов философии ноосферы – центральная идея нового мировоззрения. Таков реальный контекст обсуждаемого в нашей статье предложения о внедрении теории гармонии в систему образования, понимаемого нами как конкретный шаг на пути «движения к ноосфере».

Роль «Золотого Сечения» в античной науке

Уже на начальном этапе исследований в области Гармонии Систем появляется стремление найти числовые выразители Гармонии. Одним из таких «выразителей» стала знаменитая «Золотая Пропорция». Как подчеркивает Сергей Эйзенштейн в своей статье [28], «математическое выражение этой идеи волновало ещё древних. Первое приближение к выражению этого даёт Платон в ответе на вопрос: как могут две части составить целое («Тимей», VII):

«Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться связь, которая скрепляла бы их. Это наилучшим образом может выполнить пропорция, ибо если три числа обладают тем свойством, что среднее так относится к меньшему, как большее к среднему, и наоборот, меньшее так относится к среднему, как среднее к большему, то последнее и первое будет средним, а среднее —первым и последним. Таким образом, всё по необходимости будет тем же самым, а так как оно будет тем же самым, то оно составит целое»

Наиболее ярко отношение античной науки к «Золотой Пропорции» выражено в хорошо известном высказывании Алексея Федоровича Лосева [29]:

«С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления — Золотого Сечения... Их (древних греков) систему космических пропорций нередко в литературе изображают как курьезный результат безудержной и дикой фантазии. В такого рода объяснениях сквозит антинаучная беспомощность тех, кто это заявляет. Однако понять данный историко-эстетический феномен можно только в связи с целостным пониманием истории, то есть, используя диалектико-материалистическое представление о культуре и ища ответа в особенностях античного общественного бытия».

Таким образом, Лосев в своем высказывании в очень компактной форме выразил главную идею античной космологии: «мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления – Золотого Сечения». Сейчас «новые русские исследователи» пытаются оспаривать эту точку зрения, ссылаясь на то, что Лосев является «дилетантом» и не читал «первоисточников» (?). И это говорится об ученом, труды которого в области эстетики греческой культуры и Возрождения являются всемирно известными, а сам Алексей Лосев по праву признан научным гением 20-го столетия!

4. «Закон структурной гармонии систем» Эдуарда Сороко

Возрождение пифагорейского учения о числовой гармонии мироздания в современной науке

Во второй половине 20-го века проблема Гармонии, которая относится к разряду «вечных» научных проблем и всегда находилась в поле зрения исследовательской мысли, выдвигается на передний план. В этой связи в современной науке появляется особый интерес к математической теории Золотого Сечения и связанных с ним числам Фибоначчи [30-32]. Первым почувствовал эту тенденцию в современной науке выдающийся советский математик Николай Воробьев. Его небольшая брошюра «Числа Фибоначчи» [30], изданная в 1961 г., по праву стала «научным бестселлером» 20-го столетия. Но современная философская наука также не могла пройти мимо этой важной тенденции. И поэтому появление работ Эдуарда Сороко являются вполне закономерным явлением, отражающим общую тенденцию современной науки – возрождение Пифагорейского учения о числовой Гармонии Мироздания. Но это древнее учение получает новое звучание в работах Сороко. Речь идет о неопифагорейской линии в исследовании универсума [33]. В чем же суть этой «неопифагорейской линии»?

Законы сохранения

Главная идея Сороко состоит в том, чтобы рассмотреть реальные системы с «диалектической точки зрения». Как известно, всякий объект природы может быть представлен как диалектическое единство двух противоположных сторон A и B. Это диалектическая связь может быть выражена в следующем виде:

A + B = U (univesum)

(11)

Как подчеркивает Сороко, «здесь А и В – различия внутри единства, взаимоисключающие, но и взаимодополняющие, связанные противоположности, логически непересекающиеся классы или состояния субстрата некоторого целого» [1, c.150]. И далее: «соотношение (11) широко применимо к реальности во всех случаях, где речь идет об исследовании структуры ее объектов: вероятность и невероятность событий; масса и энергия; ядро атома и его оболочка; вещество и поле; анод и катод; животные и растения как виды «живой материи»; автотрофные и гетеротрофные организмы; организмы с наличием в клетках ядер (эукариоты) и без наличия таковых (прокариоты); духовное и материальное начала в системе ценностей; прибыль и себестоимость, образующие в совокупном действии цену и т.п.».

Наиболее характерным примером общего «закона сохранения» (11) является «закон сохранения информации», который может быть представлен в виде:

I + H = log n

(12)

где I – количество информации, а H – энтропия некоторой системы, которая может находиться в одном из n дискретных состояний.

Энтропия системы H связана с вероятностями р₁, р₂, р₃,..., р_n отдельных состояний системы известным соотношением:

(13)

В нормированной форме выражение (12) может быть представлено в виде:

R + ` H = 1

(14)

Первое слагаемое R=I/log n Клод Шеннон назвал избыточностью, а второе слагаемое ` H =H/log n – относительной энтропией.

Следует подчеркнуть, что Сороко не случайно обращается в своих исследованиях к понятию «энтропии», которое было введено в науку задолго до появления «теории информации», созданной американским математиком Клодом Шенноном [34].

Идея построения специальной функции, способной выражать термодинамическое состояние реальных систем («тепловых машин»), как и сам термин «энтропия», принадлежит Клаузиусу, который первым понял глубокое содержание работ Сади Карно. Клаузиус вместе Томсоном сформулировал «Второе Начало Термодинамики». Дальнейшее развитие понятия «энтропия» принадлежит австрийскому физику Больцману, который ввел так называемую H-функцию, характеризующую состояние замкнутой системы. Выразив эту функцию через термодинамическую вероятность W, Больцман придал энтропии статистический смысл.

Именно понятие «энтропии» и связанное с ним понятие «информация» были использованы Сороко в качестве обобщенных «измерителей» структурного разнообразия систем. Сороко пишет: «Глубокая внутренняя связь между информацией и строением (структурой) систем – в тождестве оснований. Чрезвычайно перспективным оказывается поиск фундаментального базиса («алфавита») структурных элементов систем природы. Комбинациями этих элементов создаются более сложные образования, а в конечном счете – все многообразие окружающего мира. Становится ясным, что четко дифференцированные в своем качестве структурные уровни систем объективного мира, подчиняющиеся законам самоорганизации, — это уровни ансамбля {р₁, р₂,..., р_n}, оптимизирующегося в естественном процессе развития этих систем на основе некоторых глубоко скрытых механизмов, которые, однако, могут быть выражены аналитически средствами общей теории групп, теории инвариантов, алгоритмов, языково-кодовых моделей, теории симметрии».

Таким образом, главная мысль Сороко состоит в следующем: «Четко дифференцированные в своем качестве структурные уровни систем объективного мира, подчиняющиеся законам самоорганизации, — это уровни ансамбля {р₁, р₂,..., р_n}, оптимизирующегося в естественном процессе развития этих систем на основе некоторых глубоко скрытых механизмов».

Что же это за «глубоко скрытые механизмы», которые приводят к оптимизации систем природы? Ответ на этот вопрос Сороко дает в главе 5 «Природа структурной гармонии» своей книги [1].

Математические основы структурной гармонии систем

Возникает вопрос, каким должно быть соотношение между частями диалектического противоречия А и В в «законе сохранения» (11) или между избыточностью R и относительной энтропией` H в «законе сохранения информации» (14), чтобы система находилась в устойчивом, «гармоничном» состоянии?

Для ответа на этот вопрос Сороко предлагает распространить «принцип кратных соотношений», широко проявляющийся во многих законах природы, на системы любой природы, подчиняющиеся «законам сохранения» (11), (12), (14). Сороко утверждает:

«Но вероятность и относительная энтропия, а следовательно, и избыточность, представляющая меру организации системы, сравнимы (по мере), в силу чего на последнюю также распространяется принцип «квантования». Итак, согласно принципу кратных соотношений, состоятельна билогарифмическая связь

log R = (s+1) log` H;

(15)

в другом, симметричном случае

log` Н = (s+1) log R

(16)

Связь R=f(` H) принимает простую (степенную) форму:

R = ` Hs+1

(17)

Либо

` H = Rs+1

(18)

где ранг кратности s = 0, 1, 2, …».

В этом высказывании и состоит главная идея «теории Сороко» — распространение «принципа кратных отношений» на системы любой природы.

В чем качественный смысл соотношений (17), (18)? Смысл очень простой. Для того, чтобы система, удовлетворяющая «закону сохранения» (14), находилась в устойчивом, то есть, «гармоничном» состоянии, между «избыточностью» R и «относительной энтропией» ` Н должно выполняться одно из соотношений (17) или (18).

А теперь подставим «условия гармоничности» (17), (18) в «закон сохранения» (14). После подстановки мы получаем два алгебраических уравнения:

` Hs+1 + ` Н – 1 = 0

(19)

Rs+1 + R – 1 = 0

(20)

Еще раз обратимся к физическому смыслу «уравнений гармонии» (19), (20). Сороко поясняет:

«Две равноправные системы уравнений... соответствуют объективно существующим в мире двум типам структурных связей, которыми управляют два рода законов – жесткой детерминации и стохастики. Уравнения (19) и (20) моделируют поэтому два возможных направления эволюции систем.

В одном случае это направление совпадает с процессом постепенного уменьшения энтропии и соответственно возрастания избыточности, выражающей меру организации систем. Такой процесс, выходящий за пределы «термодинамической формы» движения, типичен для управляемых систем, изменяющих свои состояния под воздействием сосредоточенных команд и под давлением обратных связей, корректирующих их поведение.

В другом же случае – с процессами простого термодинамического уравновешивания (деградация, дезорганизация, деструктуризация), типичными для «косной» неорганической природы, в которой утрата порядка, распад, хаотизация идут в полном согласии со вторым началом термодинамики».

А теперь выясним математическую природу «уравнений гармонии» (19), (20). Если неизвестные в уравнениях (19), (20) обозначить через y, то оба уравнения сводятся к одному алгебраическому уравнению:

ys+1 + y – 1 = 0

(21)

Это и есть то алгебраическое уравнение, которое принято называть в настоящее время «уравнением Сороко». Ясно, что корни уравнения (21), которые мы обозначим через b _s, представляют собой некоторые числовые инварианты «гармоничных» систем.

Чтобы выяснить математическую природу числовых инвариантов b _s, сравним «уравнение Сороко» (21) с алгебраическим уравнением (7), которое иногда называют (спасибо!) «уравнением Стахова». Если в «уравнении Сороко» сделать замену переменной, то есть вместо y подставить значение , то после несложных преобразований мы получим «уравнение Стахова» (7) (если вместо s подставить р). Вот в этом и состоит настоящая научная интрига! Оказывается, что уравнения (19), (20), (21), выведенные Сороко для моделирования устойчивых, то есть гармоничных состояний системы любой природы, после несложных преобразований сводятся к уравнению (7), выведенному Стаховым при исследовании треугольника Паскаля и при решении задачи о «золотом р-сечении отрезка», задаваемой (9). Но из этих рассуждений вытекает, что числовые инварианты» Сороко b _р, связаны с «золотыми р-пропорциями» t _р, которые являются корнями уравнения (7), следующим простым соотношением:

(22)

Подобно тому, как числа 1, 618 и 0,618 называют одним и тем же словом «золотая пропорция», уместно этот же подход использовать и для названия чисел t _р и b _р, то есть назвать их «обобщенными золотыми пропорциями» или «золотыми р-пропорциями», что и сделано в книге [1].

В соответствии с концепцией Сороко, корни уравнения (21), которые связаны с введенными выше золотыми р-пропорциями t _р соотношением обратной пропорциональности (22), и выражают закон структурной гармонии систем.

Подведя итог изложенному, Сороко формулирует «Закон структурной гармонии систем» в следующей словесной форме:

«Обобщенные золотые сечения суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоничное строение, стационарный режим существования, структурно-функциональную... устойчивость».

Значения структурных инвариантов b _s для начальных значений s задаются с помощью следующей таблицы.

Рассмотрим приложение закона Сороко для термодинамических и информационных систем. Как известно, состояние термодинамической и информационной системы выражается с помощью понятия энтропии, которое задается выражением (13).

Как известно, энтропия (13) достигает своего максимального значения

Hmax = log N

(23)

для случая, когда вероятности состояний системы (или букв) равны между собой, то есть

Используя понятие относительной энтропии

,

(24)

мы можем записать следующее очевидное равенство:

(25)

В соответствии с «законом структурной гармонии систем» каждая система переходит в свое «гармоничное состояние» в случае, когда ее относительная энтропия (24) удовлетворяет уравнению структурной гармонии систем (21), то есть равна одному из структурных инвариантов b _s. Из этих рассуждений вытекает следующее выражение для энтропии «гармоничной» системы:

.

(26)

Ясно, что для заданного параметра s проблема получения множества значений p_i (i = 1, 2,..., n), дающих оптимальное значение энтропии, имеет много решений. Однако, тем не менее, соотношение (26) играет роль некоторой «целевой» функции для решения различных научных и технических проблем, потому что оно указывает путь поиска «оптимальных» вариантов.

Сороко приводит в своей книге «Структурная гармония систем» [1] ряд интересных примеров из различных областей науки, демонстрирующих действие своего закона. Например, рассмотрим такой объект как сухой воздух, который является основой жизни на земле. Является ли структура воздуха оптимальной? Теория Сороко дает положительный ответ на это вопрос. Действительно, химический состав сухого воздуха таков: азот 78,084%; кислород — 20,948%; аргон — 0,934%; углекислый газ — 0,031%; неон — 0,002%; гелий — 0,001%. Если теперь рассчитать энтропию воздуха в соответствии с формулой (13) и вычислить его приведенную энтропию (24), разделив значение H на log N = log 6, то полученное значение приведенной энтропии будет равно 0,683, что с высокой точностью соответствует инварианту b ₂ = 0,682. Это означает, что в процессе самоорганизации сухой воздух приобрел оптимальную, то есть «гармоничную» структуру. Этот пример является весьма показательным в том отношении, что «теория Сороко» может быть уже сейчас использована для контроля за состоянием биосферы, в частности, воздушного и водного бассейна. Ясно, что практическое использование «закона структурной гармонии систем» может принести уже сейчас существенный выигрыш при решении многих технологических, экономических, экологических и других задач, в частности, совершенствовать технологию изготовления структурно-сложных продуктов, контролировать биосферу и т.д.

Идея «развития системы»

Таким образом, согласно Сороко система может находиться в различных «гармонических» состояниях, каждому из которых соответствует свой инвариант b _s: 0,618; 0,6823; 0,7245 и т.д. Можно предположить следующий вариант процесса «развития системы». В процессе самоорганизации система переходит в первое «гармоничное» состояние, соответствующее инварианту 0,618. В дальнейшем под влиянием различных внешних факторов система может выйти из первого «гармоничного» состояния и перейти в состояние «дисгармонии», где она теряет многие из своих положительных качеств. Далее в процессе развития система может перейти в следующее «гармоническое» состояние, соответствующее инварианту 0,6823 и т.д. Поэтому согласно Сороко «процесс развития» — это последовательный переход системы из одного «гармонического» состояния в следующее через промежуточные «дисгармонические» состояния.

5. Эдуард Сороко – Пифагор 20-го века?

Итак подведем некоторые итоги. В последней четверти 20-го века развивающееся в течение более двух тысячелетий Учение о Гармонии пополнилась новым фундаментальным результатом — «Законом Структурной Гармонии Систем», открытым белорусским философом Эдуардом Сороко. Необходимо отметить две принципиальные особенности этого открытия:

1. Начиная с Пифагора и Платона, ученые связывали понятие гармонии с золотой пропорцией 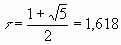(вспомним высказывание Лосева), которое считалось единственным инвариантом любой «гармоничной» системы. «Закон Сороко» утверждает, что «гармоничное» состояние системы, соответствующее классической золотой пропорции, не является единственным и что для одной и той же системы теоретически может существовать бесконечное количество «гармоничных» состояний, соответствующих различным числовым инвариантам b _s (или b _р). При этом сам «процесс развития» можно рассматривать как процесс последовательного перехода системы из одного «гармоничного» состояния в другое.
2. Числовые инварианты b _р связаны соотношением обратной пропорциональности (22) с «золотыми р-пропорциями» t _р. Но как показано в работе [2], «золотые р-пропорции» t _р выражают некоторые глубокие свойства треугольника Паскаля, который является одним из главных математических объектов комбинаторики. Таким образом, «Закон Сороко» имеет фундаментальную связь с одним из важнейших математических объектов. Этот факт является дополнительным свидетельством фундаментальности «Закона структурной гармонии систем», который имеет отношение ко всем объектам Науки и Природы.

Казалось бы, современная наука и технология должна были бы с огромным интересом отнестись к «закону Сороко» и его практическому использованию. К сожалению, ничего подобного не произошло. Мне кажется, что существует две причины прохладного отношения современной науки к «закону Сороко». Первая причина состоит в том, что Сороко – не просто философ, а еще и математик (он закончил физико-математический факультет педагогического университета). Поэтому его многие «философствующие коллеги» с их «марксистско-ленинским образованием», весьма далеким от математики и полученным во многих случаях в Высших партийных школах, просто оказались неспособными понять математическую теорию Сороко. С другой стороны, современная «материалистическая наука» всегда с подозрительностью относилась к «золотому сечению» и давно выбросила его на свалку сомнительных научных концепций вместе с астрологией и всякими там «эзотерическими науками». Поэтому «Закон структурной гармонии систем» оказался в некоторой изоляции.

История науки показывает, что многие великие научные открытия, как правило, значительно опережают текущий уровень научного познания и на начальном этапе воспринимаются современниками с большой долей скептицизма (вспомним Лобачевского, Абеля, Галуа, Максвелла и др. крупных ученых). Видимо, то же самое произошло и с «Законом структурной гармонии систем», открытым белорусским философом Эдуардом Сороко, который, однако, за открытие этого закона и огромный вклад в развитие современной теории Гармонии и Золотого Сечения по праву может быть назван Пифагором 20-го века.

Литература

1. Сороко Э.М. Структурная гармония систем. Минск, Наука и техника, 1984.
2. Стахов А.П. Введение в алгоритмическую теорию измерения. Москва, Советское Радио, 1977 г.
3. Стахов А.П. Алгоритмическая теория измерения. Москва, Знание, серия «Математика и кибернетика», вып.6, 1979 г.
4. Stakhov A.P. The Golden Section in the measurement theory. An International Journal «Computers & Mathematics with Applications», Volume 17, No 4-6, 1989.
5. Стахов А.П. Коды золотой пропорции. Москва, Радио и связь, 1984 г.
6. Stakhov A.P. The Golden Section and Modern Harmony Mathematics. Applications of Fibonacci Numbers, Volume 7, 1998.
7. Стахов А.П. Сакральная геометрия и математика гармонии // «Академия Тринитаризма», М., Эл № 77-6567, публ.11176, 26.04.2004 (http://trinitas.ru/rus/doc/0202/010a/02020028.htm).
8. Стахов А.П. Математика Гармонии как новое междисциплинарное направление современной науки // «Академия Тринитаризма», М., Эл № 77-6567, публ.12371, 19.08.2005 (http://www.trinitas.ru/rus/doc/0232/004a/02320001.htm)
9. Stakhov A. The Generalized Principle of the Golden Section and its applications in mathematics, science, and engineering. Chaos, Solitons & Fractals 2005, 26 (2): 263-289.
10. Stakhov A. Fundamentals of a new kind of Mathematics based on the Golden Section. Chaos, Solitons & Fractals 2005, 27 (5): 1124-1146.
11. Витенько И.В., Волков А.А., Стахов А.П. Оптимальные алгоритмы функционирования преобразователей «напряжение-код»ю В кни. «Тезисы докладов V научно-технической конференции «кибернетические пути совершенствования измерительной аппаратуры». ЛОП НТО, Приборпром, 1966.
12. Витенько И.В., Стахов А.П. Теория оптимальных алгоритмов аналого-цифрового преобразования. В кн. «Приборы и системы автоматики», вып. 2, изд-во Харьковского ун-та, 1970.
13. V.C. Harrys and Carolyn C. Styles. A generalization of Fibonacci numbers. Fibonacci Quarterly, 1964, Vol.2, No.4, 277-289
14. V.C. Harrys and Carolyn C. Styles. Generalized Fibonacci sequences associated with a generalized Pascal triangle. Fibonacci Quarterly, 1966, Vol.4, No.3, 241-248.
15. V.E. Hoggat, Jr. and Marjorie Bicknell. Diagonal Sums of Generalized Pascal Triangles, Fibonacci Quarterly, 1969, Vol.7, No.4, 341-358.
16. V.E. Hoggat, Jr. A new angle on Pascal’s Triangle. Fibonacci Quarterly, 1968, Vol.6, No.4, 221-234.
17. Д.Пойа. Математическое открытие. М., Наука, 1970.
18. Stakhov A., Rozin B. The «golden» algebraic equations. Chaos, Solitons & Fractals 2005, 27 (5): 1415-1421.
19. Stakhov A., Rozin B. Theory of Binet formulas for Fibonacci and Lucas p-numbers. Chaos, Solitons & Fractals 2005, 27 (5): 1162-1177.
20. Stakhov AP. Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic. The Computer Journal 2002, Vol. 45, No. 2: 222-236.
21. Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. Украинский математический журнал, том. 56, 2004 г.
22. Стахов А.П., Ткаченко И.С. Гиперболическая тригонометрия Фибоначчи. Доклады Академии наук УССР, том 208, № 7, 1993 г.
23. Stakhov A, Rozin B. On a new class of hyperbolic function. Chaos, Solitons & Fractals 2004, 23(2): 379-389.
24. Stakhov A.P., Massingua V., Sluchenkova A.A. Introduction into Fibonacci Coding and Cryptography». Харьков, Изд-во «Основа» Харьковского университета, 1999 г.
25. Волошинов А.В. Математика и искусство. М., Просвещение, 2000.
26. Шестаков В.П. Гармония как эстетическая категория. М., Наука, 1973.
27. Боднар О.Я. Учение о гармонии – в систему образования // «Академия Тринитаризма», М., Эл № 77-6567, публ.12775, 02.01.2006
28. Сергей Эйзенштейн. Сергей Эйзенштейн о «золотом сечении» // «Академия Тринитаризма», М., Эл № 77-6567, публ.13357, 29.05.2006
29. Лосев А.Ф. История философии как школа мысли. Коммунист, 1981, №11.
30. Воробьев Н.Н. Числа Фибоначчи. Москва, Наука, 1978.
31. Hoggat, V. E. Fibonacci and Lucas Numbers, Houghton-Mifflin, Palo Alto, California, 1969.
32. Vajda, S. Fibonacci & Lucas Numbers, and the Golden Section. Theory and Applications. Ellis Horwood limited, 1989.
33. Э.М. Сороко, Неопифагорейская линия в исследовании универсума // «Академия Тринитаризма», М., Эл № 77-6567, публ.13364, 30.05.2006
34. Шеннон К. Работы по теории информации и кибернетике. М. 1963.