Институт Золотого Сечения - Математика Гармонии

Стахов А.П.

---

Содержание

1. Введение
2. Понятие Гармонии
3. Комбинаторный подход к математике Гармонии
4. Основные понятия комбинаторики
5. Числа Фибоначчи в треугольнике Паскаля
6. Золотые р-пропорции
7. Обобщенный принцип Золотого Сечения
8. «Принцип асимметрии» живой природы
9. «Золотые» алгебраические уравнения
10. Закон структурной гармонии систем
11. Гиперболические функции Фибоначчи и Люка и новая геометрия живой природы
12. «Золотые» проекты или роль математики Гармонии для развития современной науки
13. Литература

---

	Алгебру и Геометрию постигла одна и та же участь. За быстрыми успехами вначале следовали весьма медленные и оставили науку на такой ступени, где она еще далека от совершенства. Это произошло от того, что Математики все свое внимание обратили на высшие части Аналитики, пренебрегая началами и не желая трудиться над обрабатыванием такого поля, которое они уже раз перешли и оставили за собою.
	Николай Лобачевский

1. Введение

Как известно, математика — одно из выдающихся творений человеческого интеллекта, результат тысячелетней интенсивной и напряженной работы математических гениев человечества. Ее роль в развитии науки огромна. И недаром ее называют «царицей наук». Какова цель математики? Ответ на этот вопрос далеко не прост. Возможно, цель математики состоит в том, чтобы открывать «математические законы Мироздания» и конструировать математические модели окружающего нас физического мира. Ясно, что прогресс человеческого общества зависит от знания этих универсальных закононв.

Современная математика переживает сложный этап в своем развитии. Затянувшийся кризис в ее основаниях, связанный прежде всего с парадоксами в Канторовской теории множеств, увлечение математиков неоправданными абстрагированиями и обобщениями привели к разрыву связей «царицы наук» с «естественными науками», которые всегда были источником новых математических идей. Ситуация в математике оказалась настолько серьезной, что многие известные математики 20-го века вынуждены были заявить о серьезном кризисе в математике и даже об ее изоляции от общего хода научно-технического прогресса. В этой связи появление книги «Математика: Потеря определенности» [1], написанной известным «математическим авторитетом» Морисом Клайном, почетным профессором Института математических наук имени Куранта (Нью-Йоркский Университет), является весьма симптоматичным. По этому поводу также весьма интересны рассуждения известного российского ученого проф. Р.Г. Баранцева. В свой неопубликованной статье «На пути к мягкой математике» он пишет: «В своём стремлении к однозначной определённости, безусловной объективности, предельной полноте описания традиционная наука отрывалась от реальной жизни с её гибкостью, открытостью, свободой воли. И оказалась банкротом перед лицом глобального кризиса, не сумев ни предсказать, ни разрешить назревшие проблемы. Кризис заставляет признать, что для изучения жизнеспособных, органических, развивающихся объектов нужна иная методология, новая парадигма».

В сложившейся ситуации представители других научных дисциплин, а именно, физики, химии, биологии, инженерии и даже искусства начали создавать так называемую естественную математику, которая может быть использована для математического моделирования физических, биологических, химических и других процессов. В последние годы получила широкое распространение идея мягкой математики [2, 3]. Как одна из основных тенденций развития современной науки, широко обсуждается идея гуманитаризации математики [4]. В этой связи книга «Метаязык живой природы» [5], написанная известным российским архитектором И.Ш. Шевелевым, тоже может быть рассмотрена как попытка создать один из возможных вариантов естественной математики.

В процессе своего исторического развития человечество осознало, что его окружает огромное количество «миров»: геометрического пространства, механических и астрономических явлений, стохастических процессов, информации, электромагнитных явлений, «мир» ботаники и биологии, «мир» искусства и т.д. Для моделирования и математического описания каждого из этих «миров» математики всегда создавали соответствующие математические теории, наиболее адаптированные для моделирования явлений и процессов того или иного «мира». Для моделирования геометрического пространства Евклид написал свои знаменитые Начала. Для моделирования механических и астрономических явлений Ньютон создал теорию гравитации и дифферециальное и интегральное исчисление. Теория Максвелла была создана с целью моделирования электоромагнитных явлений; теория вероятностей была создана для описания явлений стохастического «мира». В 19-м столетии Лобачевский создал неевклидову геометрию, которая является более глубокой моделью окружающего нас геометрического пространства. И эти примеры можно было бы продолжить. Возникает вопрос: а нельзя ли создать «Математику Гармонии», то есть математику, предназначенную для моделирования и описания «Мира Гармонии», который нас окружает?

Настоящая статья является развитием статьи автора «Сакральная Геометрия и Математика Гармонии», выставленной на сайте «Академии Тринитаризма» http://trinitas.ru/rus/doc/0202/010a/02020028.htm, а также других работ автора [6-25] в этом направлении. Главная задача статьи — ознакомить читаталей с «комбинаторным подходом», лежащим в основе Математики Гармонии, и фундаментальными принципами, лежащими в основе данного научного направления. Статья написана популярно и предназначена для широкогой круга читателей – от школьника до академика.

2. Понятие Гармонии

С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали чисто утилитарную цель – служить хранилищем воды, оружием на охоте и т.д., демонстрируют стремление человека к красоте. На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Уже в Древней Греции изучение сущности красоты, прекрасного, сформировалось в самостоятельную ветвь науки – эстетику, которая у античных философов была неотделима от космологии. Тогда же родилось представление о том, что основой прекрасного является гармония. Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый – красоту в истине.

Красота скульптуры, красота храма, красота картины, симфонии, поэмы … Что между ними общего? Разве можно сравнивать красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов – от цветка ромашки до красоты обнаженного человеческого тела?

Существует легенда, что однажды Будда провел проповедь без единого слова. Он просто протянул цветок своим прихожанам. Это был известный «Цветок церемонии», то есть церемонии на языке форм, немой язык цветов. Если рассматривать цветок вблизи и другие естественные и созданные человеком творения, то можно найти единство и порядок, свойственные всем этим предметам. Этот порядок и единство и есть Гармония, определяющая Красоту.

Известный итальянский теоретик архитектуры Леон-Баттиста Альберти, написавший много книг о зодчестве, говорил о Гармонии следующее:

«Есть нечто большее, слагающееся из сочетания и связи трех вещей (числа, ограничения и размещения), нечто, чем чудесно озаряется весь лик красоты. Это мы называем гармонией, которая, без сомнения, источник всякой прелести и красоты. Ведь назначение и цель гармонии – упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту …Она охватывает всю жизнь человеческую, пронизывает всю природу вещей. Ибо все, что производит природа, все это соизмеряется законом гармонии. И нет у природы большей заботы, чем та, чтобы произведенное ею было совершенным. Этого никак не достичь без гармонии, ибо без нее распадается высшее согласие частей».

Впервые последовательное представление о мире, как внутренне противоречивом, гармоничном целом, было развито в греческой науке. Пифагорейская доктрина о числовой Гармонии Мироздания имела большое значение для эстетики, поскольку она была первой попыткой понять концепцию Гармонии. Пифагорейцы выдвинули идею о гармонической конструкции Вселенной, включая не только природу человека, но и весь Космос в целом. Согласно пифагорейцам, Гармония есть внутренняя связь вещей, без которой Космос не существует. Наконец, согласно Пифагору, Гармония имеет численное выражение, то есть она интегрально связана с концепцией числа.

3. Комбинаторный подход к Математике Гармонии

«День рождения» Математики Гармонии

С учетом повышенного интереса современной науки к сакральной геометрии и «священным знаниям», содержащимся в Библии, Талмуде и Китайской «Книге Перемен», не является удивительным возникновение в современной математике нового математического направления, названного Математикой Гармонии. «Днем рождения» новой математики можно считать 17 июля 1996 г., когда автор сделал доклад «The Golden Section and Modern Harmony Mathematics» на 7-й Международной конференции «Числа Фибоначчи и их приложения» (Австрия, Грац, 15-19-го июля 1996 г.). Именно в этой лекции [12] впервые были сформулированы основные идеи, понятия и математические теории, образующие в совокупности основу «Математики Гармонии».

Анализ понятия «Гармония»

Попытаемся изложить «методологические основы» новой математики. Как известно, математика изучает количественные аспекты того или иного явления. И начиная математический анализ понятия Гармонии, мы должны сконцентрировать наше внимание на количественных аспектах этого понятия. Что такое Гармония с количественной точки зрения? Чтобы ответить на это вопрос, мы начнем с выяснения значения слова «Гармония». Как известно, слово «Гармония» имеет греческое происхождение. При этом греческое слово a r m o u i a означаетсвязь, согласие.

Существуют различные определения понятия «Гармония». Однако большинство из них содятся к следующему определению, приведенному в Большой Советской Энциклопедии:

«Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В Гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия».

Анализ значения слова «Гармония» и его определения показывает, что наиболеее важными, «ключевыми» понятиями, которые лежат в основе Гармонии, являются следующие: связь, согласие, комбинация, упорядоченность.

Возникает вопрос: какой раздел математики изучает подобные понятия? Поиски ответа на этот вопрос приводят нас к комбинаторному анализу. Как известно, «комбинаторика занимается различного вида сочетаниями (соединениями), которые можно образовать из элементов некоторого конечного множества. Термин «комбинаторика» происходит от латинского слова combinary – сочетать, соединять».

Из этого рассмотрения вытекает, что латинское слово combinary и греческое слово a r m o u i a имеют близкие значения и могут быть переведены как комбинация илисоединение. Это дает нам право выдвинуть гипотезу, что именно «Законы комбинаторного анализа» могут быть использованы для анализа понятия «Гармония» с количественной точки зрения.

4. Основные понятия комбинаторики

Комбинаторика занимается различного вида сочетаниями, которые можно образовать из элементов некоторого множества. Некоторые элементы комбинаторики были известны в Индии еще во 2-м веке до н.э. Индийцы умели вычислять числа, которые мы обозначаем , то есть сочетания из n элементов, взятых по m, и знали формулу

+ + … + = 2n.

(1)

Предполагают, что индийские математики изучали соединения в связи с применением их в поэтике, науке о структуре стихов и поэтических произведений, например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы, состоящей из n слогов.

Примером эффективного использования формулы (1) является теория двоичного кодирования, основа современных компьютеров. Действительно, рассмотрим множество n-разрядных двоичных слов, начиная с 00 … 0 и заканчивая 11 … 1. Как известно, число элементов этого множества равно 2ⁿ. Разобьем это множество на (n+1) непересекающихся подмножеств: к первому подмножеству отнесем все двоичные слова, состоящие из 0 единиц и n нулей (ясно, что этому условию удовлетворяет только одна кодовая комбинация 00…0, то есть, число элементов этого подмножества равно =1), ко второму подмножеству отнесем все двоичные слова, содержащие одну единицу и (n-1) нулей (число элементов этого подмножества равно ), к (m+1)-му подмножеству отнесем все n-разрядные двоичные слова, каждое из которых содержит m единиц и (n-m) нулей (число кодовых комбинаций, входящих в это подмножество, равно ), наконец, к (n+1)-му подмножеству отнесем все двоичные слова, состоящие из одних единиц (ясно, что этому условию удовлетворяет только одна кодовая комбинация 11…1, то есть, число элементов этого подмножества равно ). Из проведенных рассуждений вытекает справедливость формулы (1).

Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1666 году работы «Рассуждение о комбинаторном искусстве», в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением «размещений» впервые занимался Якоб Бернулли во второй части своей знаменитой книги «Ars conectandi» («Искусство предугадывания»), опубликованной в 1713 г. Он же ввел соответствующий термин и употреблял в нашем смысле также термин «перестановка». Термин же «сочетание» ввел Б. Паскаль в своем «Трактате об арифметическом треугольнике» (1665 г.).

Известна формула

,

(2)

где n!=1ґ 2ґ 3ґ …ґ n – факториал от n.

Заметим, что термин «факториал» происходит от латинского factor – производящий.

Бином Ньютона

Слово «бином» (от латинского bis – дважды и греческого «номос» — член) означает «двучлен».

Запишем следующие выражения:

(a+b)0 = 1 (a+b)1 = 1a + 1b (a+b)2 = 1a2 + 2ab + 1b2 (a+b)3 = 1a3 + 3a2b + 3ab2 + 1b2

(3)

Заметим, что первые два выражения из (3) тривиальны, а остальные два нам хорошо известны из курса алгебры средней школы.

Возникает вопрос: чему равно (a+b)ⁿ? Ответ на этот вопрос дает знаменитая математическая теорема, известная под названием «Бинома Ньютона», представляющая разложение целой положительной степени n бинома a+b:

(a+b)n = an +an-1b + an-2b2 + … + an-kbk + … + abn-1 + bn.

(4)

В этой формуле появляются любопытные коэффициенты , которые называются биномиальными коэффициентами.

Заметим, что в названии «Бином Ньютона» заключена историческая несправедливость, так как эта формула была известна задолго до Ньютона многим ученым разных стран, в том числе Ал-Каши, Тарталье, Ферма, Паскалю. Заслуга Ньютона состоит в том, что он распространил ее на любое действительное число n, то есть он показал, что формула (4) верна и тогда, когда n является рациональным или иррациональным, положительным или отрицательным.

Формулы (3) являются частными случаями общей формулы (4). В частности, при n=1 формула (4) принимает вид:

(a+b)¹ = a + b = 1a + 1b,

откуда вытекает, что =1 и =1.

При n=2 формула (4) принимает вид:

(a+b)² = a² + ab + b² = 1a² + 2ab + 1b²,

откуда вытеакает, что = 1, = 2, = 1.

Таким образом, разложение (4) легко получить, если мы научимся вычислять биномиальные коэффициенты .

Треугольник Паскаля

Ответ на вопрос, как найти значение для любых целых неотрицательных n и k еще в 17 в. дал знаменитый французский физик и математик Блез Паскаль (1623-1662). Паскаль обнаружил, что биномиальные коэффициенты обладают следующими замечатешльными свойствами:

= = 1;

(5)

=;

(6)

= +.

(7)

Последнее свойство (7) называется также законом Паскаля. Именно используя соотношение (7), Паскаль предложил изящный способ вычисления биномиальных коэффициентов, расположив их в виде треугольной таблицы, называемой треугольником Паскаля. Суть этого способа состоит в следующем. Рассмотрим бесконечную таблицу чисел, построенных по «закону Паскаля» (Табл. 1).

Таблица 1

Треугольник Паскаля

Верхняя строку Табл. 1 будем считать нулевой строкой. Здесь находится единственный биномиальный коэффициент =1. Следующая строка, называемая первой, состоит из двух единиц, симметрично расположенных относительно единицы нулевой строки. Это -биномиальные коэффициенты = 1 и = 1. Каждая последующая строка состоит из двух единиц, расположенных по ее краям (это биномиальные коэффициенты типа = 1 и = 1); каждое «внутреннее» число этой строки формируется из двух чисел предыдущей строки, стоящих над этим числом слева и справа относительно этого числа, по «закону Паскаля» (7). Легко доказать следующие свойства «Треугольника Паскаля»:

1. Сумма чисел n-й строки треугольника Паскаля равна 2ⁿ, что соответствует формуле (1).
2. Все строки треугольника Паскаля симметричны, что вытекает из свойства (6).

Указанный выше «треугольник Паскаля» впервые появился в сочинении Паскаля «Трактат об арифметическом треугольнике» (1665 г.). Однако еще за столетие до выхода этого трактата эта таблица – только не в «треугольной», а в «прямоугольной» форме – была опубликована в «Общем трактате о числе и мере», написанном выдающимся итальянским математиком Николо Тарталья (1500-1557) и опубликованным уже после его смерти.

Таблица 2

Прямоугольник Тартальи

Здесь верхняя строка состоит из единиц; в каждой из остальных строк самое левое число есть единица, а каждое следующее число образуется посредством двух чисел, стоящих непосредственно перед ним и над ним. Таблицу, предложенную Тарталья, принято называть прямоугольником Тарталья.

Биномиальные коэффициенты и треугольник Паскаля широко используются в различных разделах математики, информатики и других науках. По существу, это – один из фундаментальных математических объектов, лежащих в основе точных наук. Знаменитый математик Якоб Бернулли писал:

«Эта таблица имеет ряд чудесных свойств. Только что мы показали, что она составляет существо теории соединений, но те, кто тесно соприкасаются с геометрией, знают, что она хранит ряд фундаментальных секретов этой области математики».

5. Числа Фибоначчи в треугольнике Паскаля

Прямоугольный Треугольник Паскаля

Возникает вопрос: какое отношение треугольник Паскаля имеет к числам Фибоначчи и золотому сечению? Оказывается – самое непосредственное. Более того. Именно треугольник Паскаля и является источником новых математических результатов, которые были положены автором в основу Математики Гармонии.

Как известно, существует много различных форм представления треугольника Паскаля – в виде равнобедренного треугольника (Табл. 1), в виде прямоугольника Тартальи (Табл.2) и т.д.

В наших исследованиях мы будем использовать еще один способ представления биномиальных коэффициентов в виде таблицы, напоминающей прямоугольный треугольник (Табл. 3). Такую таблицу биномиальных коэффициентов мы будем называть прямоугольным треугольником Паскаля.

Таблица 3

Прямоугольный треугольник Паскаля

Такая таблица начинается с «нулевого столбца», который содержит единственный биномиальный коэффициент = 1, и из «нулевого ряда», который содержит биномиальные коэффициенты: = 1, = 1, = 1, = 1,..., = 1,.... Заметим, что «гипотенуза» прямоугольного треугольника Паскаля (Табл. 3) состоит из биномиальных коэффициентов типа =1, =1, =1,...., = 1,....

Заметим также, что в n-м столбце сверху вниз расположены следующие биномиальные коэффициенты: , , , ,..., . Тогда, если просуммировать биномиальные коэффициенты n-го столбца рассматриваемого треугольника Паскаля, то согласно (1) мы получим «двоичное число» 2ⁿ. Если это сделать для всех столбцов, начиная с нулевого, то мы получим широко известный нам «двоичный ряд чисел»:

1, 2, 4, 8, 16, 32, 64, …., 2n, ….

(8)

Таким образом, мы можем утверждать, что треугольник Паскаля «генерирует» двоичный ряд чисел!

1-треугольник Паскаля

А теперь сдвинем каждый ряд исходного треугольника Паскаля (Табл. 3) на один столбец вправо относительно предыдущего ряда. В результате такого преобразования мы получим некоторый «деформированный» треугольник Паскаля (Табл. 4), который мы будем называть 1-треугольником Паскаля..

Таблица 4

1-треугольник Паскаля

Если мы теперь просуммируем биномиальные коэффициенты 1-треугольника Паскаля по столбцам, то, к нашему изумлению, мы обнаружим, что такое суммирование приведет нас к числам Фибоначчи:

1, 1, 2, 3, 5, 8, 13, …, Fn+1, ….

(9)

которые были получены Фибоначчи в 13 столетии при решении «задачи о размножении кроликов»!

Из этих рассуждений легко вывести также математическую формулу, которая позволяет выразить все числа Фибоначчи через биномиальные коэффициенты:

(10)

где n, m и r связаны между собой следующим соотношением: n=2m+r.

Ясно, что формула (10) столь же фундаментальна, как и рекуррентная формула, задающая ряд Фибоначчи (9).

Полученный математический результат, который был найден во второй половине 20-го столетия многими математиками практически одновременно, для нашего исследования имеет принципиальное значение. Мы обнаружили числа Фибоначчи в треугольнике Паскаля, который является главным математическим объектом комбинаторного анализа. И этот результат подтверждает правильность главной «методологической идеи» нашего исследования о том, что основой «Математики Гармонии» является комбинаторный анализ.

Р-треугольники Паскаля

А теперь «закрепим наш успех» и покажем, что треугольник Паскаля является источником новых математических результатов, которые и являются основой Математики Гармонии. Для этого продолжим наши «манипуляции» с треугольником Паскаля. Если теперь в исходном треугольнике Паскаля (Табл. 3) сдвинуть биномиальные коэффициенты каждого ряда на 2 столбца вправо относительно предыдущего ряда, то мы получим новый «деформированный» треугольник Паскаля, который мы назовем 2-треугольником Паскаля (Табл. 5).

Таблица 5

2-треугольник Паскаля

1	1	1	1	1	1	1	1	1	1	1	1	1
			1	2	3	4	5	6	7	8	9	10
						1	3	6	10	15	21	28
									1	4	10	20
												1
1	1	1	2	3	4	6	9	13	19	28	41	60

А теперь просуммируем биномиальные коэффициенты Табл. 5 по столбцам. В результате мы получим следующий числовой ряд:

1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60,...

(11)

Проведем анализ этого числового ряда. Мы видим, что он начинается с трех единиц, после которых идет число 2, которое можно представить в виде:

2 = 1 + 1.

(12)

Далее идет число 3, которое можно представить в виде:

3 = 2 + 1. (13)

(13)

Последующие числа ряда (11) можно представить в виде:

4 = 3 + 1; 6 = 4 + 2; 9 = 6 + 3; 13 = 9 + 4

(14)

и т.д.

К каким выводам приводит анализ сумм (12) – (14)? Мы видим, что каждое число ряда (11), начиная с 4-го, подчиняется следующей математической закономерности: каждое число равно сумме предыдущего числа и числа, отстоящего от него на 2 позиции слева. Подобного рода математические законономерности в математике выражаются с помощью рекуррентных формул. Если обозначить n-е число ряда (11) через F₂(n), то тогда указанную выше закономерность можно выразить с помощью следующей рекуррентной формулы:

F2(n) = F2(n-1) + F2(n-3) для nі 4;

(15)

F2(1) = F2(2) = F2(3) = 1.

(16)

В дальнейшем мы будем называть числа F₂(n), задаваемые рекуррентной формулой (15) при начальном условии (16), 2-числами Фибоначчи.

А теперь продолжим наши «манипуляции» с треугольником Паскаля. Сдвинем биномиальные коэффициенты каждого ряда исходного треугольника Паскаля (Табл. 3) на 3 столбца вправо относительно предыдущего ряда. В результате мы получим новый «деформированный» треугольник Паскаля, который мы назовем 3-треугольником Паскаля (Табл. 6).

Таблица 6

3-треугольник Паскаля

1	1	1	1	1	1	1	1	1	1	1	1	1
				1	2	3	4	5	6	7	8	9
								1	3	6	10	15
												1
1	1	1	1	2	3	4	5	7	10	14	19	26

Если теперь просуммировать по столбцам биномиальные коэффициенты 3-треугольников Паскаля; то в результате получим новую числовую последовательность:

1, 1, 1, 1, 2, 3, 4, 5, 7, 10, 14, 19, 26,...

(17)

Если обозначить n-й член последовательности (17) через F₃(n), то легко усмотреть в ряде (17) следующую закономерность. Первые четыре числа ряда (17) равны 1, то есть,

F3(1) = F3(2) = F3(3) = F3(4) = 1,

(18)

а каждое последующее число равно сумме предыдущего числа F₃(n-1) и числа F₃(n-4), отстоящего от него на 3 позиции влево. Эту закономерность можно выразить с помощью следующей рекуррентной формулы:

F3(n) = F3(n-1) + F3(n-4) для nі5

(19)

Числовую последовательность (17), задаваемую рекуррентной формулой (19) при начальных условиях (18), мы будем в дальнейшем называть 3-числами Фибоначчи.

А теперь рассмотрим ситуацию, когда в исходном треугольнике Паскаля (Табл. 3) мы сдвигаем биномиальные коэффициенты каждого ряда на р столбцов вправо относительно предыдущего ряда, где р может принимать следующие значения: 0, 1, 2, 3,.... Полученный таким путем «деформированный» треугольник Паскаля мы будем называть р-треугольником Паскаля.

Нетрудно показать (или догадаться), что суммирование биномиальных коэффициентов р-треугольника Паскаля по столбцам приведет нас к некоторому новому числовому ряду, который задается следующим рекуррентным соотношением:

Fp(n) = Fp(n-1)+Fp(n-p-1) для n>p+1;

(20)

Fp(1) = Fp(2) =... = Fp(p+1) = 1

(21)

Числовые ряды, соответствующие формулам (20), (21), были названы p-числами Фибоначчи.

А теперь посмотрим, во что вырождается рекуррентная формула (20) и начальные условия (21) для различных значений р. Ясно, что для случая р=0 рекуррентная формула (20) и начальные условия (21) принимают следующий вид:

F0(n) = F0(n-1)+F0(n-1) = 2F0(n-1) для n> 1;

(22)

F0(1) = 1

(23)

Нетрудно догадаться, что рекуррентная формула (22) при начальном условии (23) «генерирует» двоичные числа (8), которые и являются крайним частным случаем р-чисел Фибоначчи, соответствующим значению р=0.

Теперь рассмотрим случай р=1. Для этого случая выражения (20) и (21) сводятся к следующему:

F1(n) = F1(n-1)+F1(n-2) для n>2;

(24)

F1(1) = F1(2) =1

(25)

Легко усмотреть, что формулы (24), (25) «генерируют» классические числа Фибоначчи (9).

Наконец, выясним, во что вырождаются р-числа Фибоначчи для случая р=Ґ. Ясно, что для этого случая р-числа Фибоначчи задаются только формулой (21), то есть ряд Ґ -чисел Фибоначчи представляет собой бесконечную последовательность единиц.

Таким образом, «манипуляции» с треугольником Паскаля привели нас к небольшому (а может, и большому!) математическому открытию. Мы обнаружили бесконечное количество рекуррентных числовых рядов, названных р-числами Фибоначчи. При этом частными случаями р-чисел Фибоначчи являются двоичные числа (8) и классические числа Фибоначчи (9).

Это математическое открытие [7] и стало «стартовой площадкой» для новых математических результатов.

6. Золотые р-пропорции

Отношения соседних р-чисел Фибоначчи

Образуем теперь числовые последовательности, которые состоят из отношений соседних р-чисел Фибоначчи, то есть, отношений типа F_p(n)/F_p(n-1).

Начнем с простейшего случая р=0. Для этого случая р-числа Фибоначчи сводятся к классическим двоичным числам (8). Ясно, что отношения соседних двоичных чисел представляют собой числовую последовательность следующего вида:

2/1, 4/2, 8/4, 16/8, …, 2n/2n-1, …

(26)

Ясно, что отношение любых двух чисел в последовательности (26) всегда равно 2.

Рассмотрим теперь случай р=1. Как было установлено, в этом случая р-числа Фибоначчи совпадают с классическими числами Фибонаачи (9), из которых мы можем образовать следующую числовую последовательность:

1/1, 2/1, 3/2, 5/3, 8/5, 13/8, …

(27)

Хорошо известно, что числовая последовательность (27) выражает так называемый «закон филллотаксиса», то есть числовую закономерность, которая лежит в основе большинства «плотноупакованных» ботанических структур типа сосновой шишки, ананаса, головки подсолнечника, кактуса и т.д., то есть, эта последовательность широко используется Природой (или Богом) при конструировании ботанических структур. С другой стороны, эта последовательность стремится к Золотой Пропорции t = , которая является корнем «уравнения золотого сечения»:

x2 = x + 1

(28)

А теперь рассмотрим отношения соседних 2-чисел Фибоначчи:

1/1, 1/1, 2/1, 3/2, 4/3, 6/4, 9/6, 13/9, …, F2(n)/F2(n-1), ….

(29)

К чему стремится в пределе последовательность (29)? Для ответа на этот вопрос представим отношение F₂(n)/F₂(n-1) в виде:

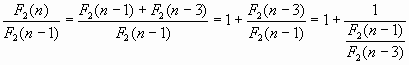(30)

При устремлении n к бесконечности отношение в левой части (30) стремится к некоторому неизвестному нам числу, которое мы обозначим через x.

Рассмотрим теперь отношение в правой части (30). Это отношение может біть представлено в виде:

(31)

Если теперь устремить n к бесконечности, то каждое из отношений и в правой части (31) в пределе стремится к тому же числу x, откуда вытекает, что отношение в левой части (31) в пределе стремится к числу x².

Возвращаясь теперь к выражению (30), мы можем записать, что в пределе (при n® Ґ) это выражение можно заменить на следующее:

,

откуда вытекает следующее алгебраическое уравнение для поиска значения числа x:

x3 = x2 + 1.

(32)

Обозначим положительный корень уравнения (32) через t ₂ и назовем его золотой 2-пропорцией. Численное решение уравнения (32) дает следующее приближенное значение для t ₂ = 1,465.

Если теперь провести те же рассуждения для отношений соседних 3-чисел Фибоначчи, задаваемых рекуррентгной формулой (19), то мы прийдем к следующему алгебраическому уравнению:

x3 = x2 + 1.

(33)

Его положительный корень t ₂ » 1,380 мы будем называть золотой 3-пропорцией.

В общем случае (для заданного целого р=0, 1, 2, 3,...), исследуя отношения соседних р-чисел Фибоначчи F_p(n)/F_p(n-1), мы прийдем к следующему алгебраическому уравнению:

xр+1 = xр + 1.

(34)

Положительный корень этого уравнения t _р мы будем в дальнейшем называть обобщенной золотой пропорцией или золотой р-пропорцией.

Подведем некоторые итоги. Из проведенного исследования вытекает, что треугольник Паскаля, который нам известен с 17-го столетия, хранит много интересных тайн, одну из которых мы только что раскрыли. Суть этого открытия состоит в том, что треугольник Паскаля «генерирует» бесконечное число новых рекуррентных числовых последовательностей, которые мы назвали р-числами Фибоначчи. Кроме того, исследование р-чисел Фибоначчи привело нас к открытию нового класса иррациональных чисел t _р, которые мы назвали золотыми р-пропорциями. С увеличением р золотая р-пропорция становится все меньше и в предельном случае (р® Ґ) t _р ® 1.

С учетом вышеизложенного можно привести значения золотых р-пропорций для некоторых значений р (Табл. 7).

Таблица 7

Золотые р-пропорции

Таким образом, между числами 2 и 1 находится бесконечное число иррациональных чисел, золотых р-пропорций, которые выражают более сложные «гармонии», чем классическая золотая пропорция t = 1,618. То есть, золотых пропорций существует бесконечное кодичество. И, как вытекает из треугольника Паскаля, все они имеют одинаковое право выражать «Гармонию». Это – первый методологический вывод, который вытекает из «Математики Гармонии».

Геометрическая формулировка задачи о золотом р-сечении

А теперь сформулируем «задачу о золотом р-сечении» геометрически. Всем хорошо известна формулировка «задачи о золотом сечении». Это такое деление исходного отрезка АВ точкой С на две неравные части АС и СВ, чтобы выполнялась следующая пропорция:

(35)

Эта задача допускает следующее обобщение. Зададимся целым неотрицательным числом р=0, 1, 2, 3,... и разделим отрезок AВ точкой C в следующей пропорции (Рис. 1):

(36)

Если обозначить и учесть, что АВ = АС + СВ, то отношение можно представить в виде:

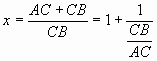(37)

Учитывая (36), выражение (37) можно записать в виде:

,

откуда непосредственно вытекает алгебраическое уравнение (34), полученное нами при исследовании отношений соседних р-чисел Фибоначчи.

Это означает, что деление отрезка в отношении (36) осуществляется в отношении золотой р-пропорции t _р.

Заметим, что пропорция (36) сводится к «дихотомии» (то есть к делению отрезка пополам) для случая p = 0 (Рис.1-a) и к классическому золотому сечению для случая p = 1 (Рис. 1-b). Учитывая это обстоятельство, деление отрезка AB точкой C в отношении (36) было названо золотым p-сечением, а положительный корень уравнения (34) — золотой p-пропорцией.

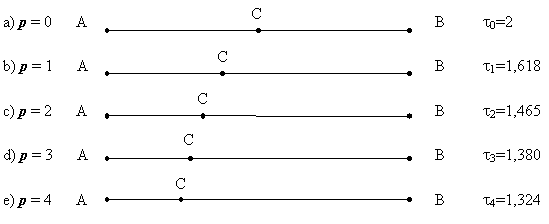
Рисунок 1. Золотые p-сечения (p = 0, 1, 2, 3,...)

Некоторые алгебраические свойства золотой р-пропорции

Подставляя золотую р-пропорцию t _р вместо x в уравнение (34), получим следующее тождество для золотой р-пропорции:

.

(38)

Разделив все члены тождества (38) на , получим следующие замечательные свойства для золотой р-пропорции:

(39)

и

.

(40)

Заметим, что для случая р=0 (t ₀=2) тождества (4.39) и (40) сводятся к следующим тривиальным формулам:

и 2 – 1 = .

При р=1 и тогда тождества (39), (40) вырождаются в широко известные тождества для золотой пропорции:

и

(41)

Будем теперь многократно умножать и делить все члены тождества (38) на t _р; в результате получим следующее замечательное тождество, связывающее степени золотой р-пропорции:

.

(42)

где n принимает значение из множетва {0, ±1, ±2, ±3,...}.

Заметим, что для случая p = 0 t _p = t ₀ = 2 и тождество (42) сводится к следующему тривиальному тождеству для двоичных чисел:

2ⁿ = 2^n-1 + 2^n-1.

Для p = 1 t ₁= t = и тождество (42) сводится к следующему тождеству, справедливому для золотой пропорции:

t n = t n-1 + t n-2,

(43)

Золотые р-прямоугольники

В статье автора «Сакральная Геометрия и Математика Гаомнии», выставленной на сайте «Академия Тринитаризма» показано, что понятие золотой р-пропорции имеет прямое отношение к сакральной геометрии [26]. Для этого рассмотрим прямоугольник с отношением сторон t _p: 1 (Рис. 2).

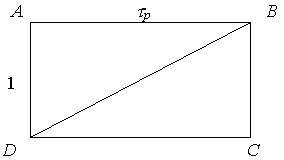
Рисунок 2. Золотой р-прямоугольник

Рассмотрим, к чему сводится золотой р-прямоугольник на Рис. 2 для частных случаев значения р.

Пусть р=0. В этом случае золотая 0-пропорция t ₀ = 2 и тогда золотой 0-прямоуголник будет представлять собой ни что иное, как «двойной» квадрат (Рис. 2), который считается священной фигурой и порождает «священное число» .

Пусть теперь р=1. В этом случае золотой р-прямоугольник сводится к такой «священной фигуре» как золотой прямоугольник, который выражает еще одно «священное число» — золотую пропорцию. Наконец, при р ® Ґ t _p ® 1 и тогда золотой р-прямоугольник вырождается в такую «священную фигуру» как квадрат, который связан со «священным числом» .

Таким образом, по крайней мере три (,,) из пяти основных геометрических отношений сакральной геометрии [26] имеют непосредственное отношение к понятию «золотая р-пропорция», которое является одним из важнейших понятий Математики Гармонии. Это означает, что Математика Гармонии может быть использована для развития сакральной геометрии. Одно из «революционных» предложений состоит в том, чтобы понятие золотой р-пропорции ввести в священную геометрию в качестве одного из основных геометрических отношений сакральной геометрии.

7. Обобщенный принцип Золотого Сечения

Уравнение целостности и мистическая единица

Так называется один из параграфов книги «Метаязык живой природы» [5], автором которой является известный российский архитектор И.Ш. Шевелев. Взяв за основу знаменитое изречение Гераклита «Из одного – все, из всего – одно», Шевелев попытался вывести из него наиболее общие принципы, лежащие в основе целостности живой природы. В качестве символа «целостности» Шевелев выбирает «Единицу» или «Монаду». Пифагорейцы учили, что 1 обозначает дух, из которого происходит весь видимый мир; единица есть разум, добро, гармония, счастье; она соединяет в себе четное с нечетным и мужское с женским. Геометрически «единица» выражает точку. Пифагорейцы называли единицу «Монадой» и считали ее матерью всех чисел.

Единица обладает рядом уникальных математических свойств, над которыми мы, возможно, и не задумывались. Приведем некоторые из них: (а) единица не относится ни к простым, ни к составным числам; (б) каждое натурально число имеет делителем единицу; (в) единица является единственным натуральным числом, имеющим только один делитель; (г) единица – единственное натуральное число, n-я степень которого равна тому же числу; (д) после умножения (или деления) какого-либо числа на 1 это число не меняется; (е) после деления какого-либо числа, не равного нулю, самого на себя получается 1. И не случайно, что именно «Единица» в свое время так поразила Галилео Галилея. В своих «Беседах» он пишет: «Если какое-либо число должно являться бесконечностью, то этим числом должна быть единица; в самом деле в ней мы находим условия и необходимые признаки, которым должно удовлетворять бескнечно большое число, поскольку оно содержит в себе столько же квадратов, сколько кубов и чисел вообще... Единица является и квадратом, и кубом, и квадратом квадрата и т.д... Отсюда заключаем, что нет другого бесконечного числа, кроме единицы. Это представляется столь удивительным, что превосходит способность нашего представления».

Принцип дихотомии и принцип Золотого Сечения

Выбрав «Единицу» в качестве символа «целостности» всего сущего, Шевелев попытался записать «Уравнение Первоосновы», то есть тождество, позволяющее выразить «Единицу» в виде суммы простейших элементов, и создать его динамическую модель.

Для этого можна использовать «Принцип Дихотомии», который основывается на следующем простейшем тождестве, связывающем «двоичные числа»:

2n = 2n-1 + 2n-1,

(44)

где n=0, ±1, ±2, ±3, ….

Для случая n=0 мы можем записать:

1 = 20 = 2 -1 + 2 -1.

(45)

В книге [5] приведена следующая «динамическая» модель «Принципа Дихотомии»:

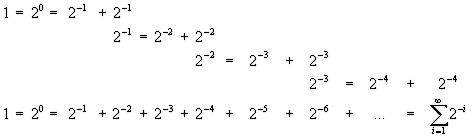(46)

которая приводит нас к следующему «Уравнению Первоструктуры»:

(46a)

В основу «Уравнения Первоструктуры» может быть положен «Принцип Золотого Сечения», который основывается на следующем тождестве, связывающем степени Золотой Пропорции t = :

t n = t n-1 + t n-2,

(47)

где n=0, ±1, ±2, ±3, ….

Для случая n=0 мы можем записать:

1 = t 0 = t -1 + t -2.

(48)

Используя тождества (47), (48), Шевелев конструирует следующую «динамическую» модель «Принципа Золотого Сечения»:

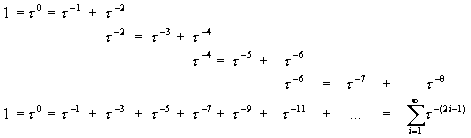(49)

которая приводит нас еще к одному «Уравнению Первоосновы»:

(50)

Заметим, что «Принцип Дихотомии», задавемый (46), (47), и «Принцип Золотого Сечения», задаваемый (49), (50), имеют огромное количество приложений (двоичная система счисления, численные методы решения алгебраических уравнений и т.д). В частности, «Принцип Дихотомии» (46), (47) лежит в основе «двоичной системы счисления»:

(51)

где a_i – двоичная цифра 0 или 1; 2ⁱ – вес i-го разряда системы счисления (51); i=0, ±1, ±2, ±3, ….

«Принцип Золотого Сечения» (49), (50) лежит в основе системы счисления Бергмана [27]:

(52)

где a_i – двоичная цифра 0 или 1; 2ⁱ – вес i-го разряда системы счисления (52); t ⁱ вес i-го разряда системы счисления (52); t = — золотая пропорция; i=0, ±1, ±2, ±3, ….

По мнению Шевелева [5], «Уравнения Первоосновы» (47), (50) имеют значение, далеко выходящее за пределы математических приложений. Шевелев утверждает: «Именно так строит себя живая природа. Все ее объекты возникают по этой схеме. Из одного начального элемента возникает «все», и это «все» создает взаимоскрепленное, взаисно необходимое, непостижимым образом соединенное и не распадающееся на составныке части неделимое целое — объект бытия. Так растет из семени дерево, из оплодотворенной клетки – сложнейше устроенное живое существо; и так же, предположительно,из одного начального состояния, из одного Нечто возникла Вселенная: современная астрофизика, непрерывно совершенствуя модель расширяющейся Вселенной, утверждает, что вещество и энергия в наблюдаемом мире могли возникнуть буквально из ничего».

Обобщенный Принцип Золотого Сечения

А теперь разделим все члены тождества (42) на . В результате получим следующее тождество, задающее «Единицу»:

.

(53)

Используя (42), (53), можно сконструировать следующую «динамическую» модель разложения «Единицы» по степениям золотой р-пропорции:

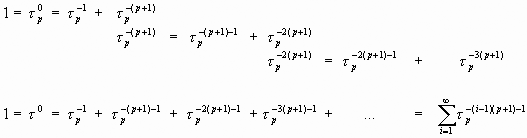(54)

Основным результатом проведенного исследования является получение более общего «Уравнения Первоосновы»:

,

(55)

которое задает более общий научный принцип – «Обобщенный Принцип Золотого Сечения».Ясно, что этот общий принцип содержит в себе в качестве частных случаев «Принцип Дихотомии» (р=0) и «Принцип Золотого Сечения» (р=1).

Примером реализации этого общего принципа является выражение для «Кода золотой р-пропорции» [8]:

,

(56)

где a_iО {0, 1} и i = 0, ± 1, ± 2, ± 3, ….

Заметим, что «двоичная система счисления» (51) и «система счисления Бергмана» (52) являются частными случаями «кода золотой р-пропорции» (56), соответсвующими значениям р=0 и р=1.

В работе [19] выражение (56) рассматривается как новый способ представления действительных чисел, откуда вытекает новая теория действительных чисел, основанная на «Обобщенном Принципе Золотого Сечения».

Если опять обратиться к книге Шевелева, то мы должны признать, что «Уравнение Первоосновы», задаваемое (55), задает нам бесконечное число «гармонических» структур, которые могут быть созданы Природой (или Богом), используя комбинаторные соотношения.

8. «Принцип асимметрии» живой природы

«Асимметрия» размножения кроликов

Как известно, числа Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, 34, … были введены известным итальянским математиком Фибоначчи в 13-м столетии при решении задачи о «размножении кроликов» [28, 29]. Эта проблема и ее решение (числа Фибоначчи) имеют два важных следствия для развития современной науки. Во-первых, эта задача дала начало математической теории биологических популяций. Во-вторых, рекуррентное соотношение Фибоначчи дало начало методу рекуррентных соотношений, который считается одним из наиболее известных методов решения комбинаторных задач.

Напомним, что «Закон размножения кроликов» сводится к следующему правилу. Каждая «зрелая пара кроликов» А ежемесячно «производит» «новорожденную пару кроликов» B. «Новорожденная пара кроликов» В в течение месяца «созревает» и затем каждый месяц приносит приплод из пары себе подобных. Тогда мы можем промоделировать процесс «размножения кроликов» с помощью двух «переходов»:

A® AB

(57)

B® A

(58)

Заметим, что переход (57) моделирует процесс возникновения «новорожденной пары кроликов» B, а переход (58) – процесс созревания «новорожденной пары кроликов» B. Переход (57) отражает «асимметрию» процесса размножения кроликов, потому что «зрелая пара кроликов» А превращается в две неидентичные пары кроликов, «зрелую пару кроликов» А и «новоржденную пару» B.

Принцип асимметрии живой природы

Используя модель «размножения кроликов» (57), (58), можна предложить следующий «Принцип асимметрии» живой природы. Зададимся целым неотрицательным числом рі 0 и рассмотрим следующую задачу:

«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой через р месяцев и еще через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?»

Ясно, что при р=1 обощенный вариант задачи о «размножении кроликов» совпадает с классической задачей Фибоначчи [28, 29].

Заметим, что случай р=0 соответствует той идеализированной ситуации, когда «кролики» становятся «зрелыми» сразу же после рождения. Можна промоделировать этот случай, используя следующий переход:

A® AA

(59)

Ясно, что переход (59) отражает «симметрию» размножения кроликов, когда каждая пара «новорожденных кроликов» превращается в «зрелую пару» А сразу же после рождения. Очень просто показать, что в этом случае «кролики» размножаются в соответствии с «Принципом Дихотомии», то есть, ежемесячно удваиваются: 1, 2, 4, 8, 16, 32,....

Рассмотрим теперь случай р>0. Проанализируем более детально сформулированную выше задачу, принимая во внимание, новые правила «размножения кроликов». Ясно, что «процесс размножения» описывается более сложной системой «переходов». Действительно, пусть A – пара «зрелых кроликов» и В – пара «новорожденных кроликов». Тогда переход (57), как и раньше, будет моделировать процесс ежемесячного возникновения «новорожденной пары кроликов» В из каждой пары «зрелых кроликов» А.

Рассмотрим теперь процесс трансформации «новорожденной пары кроликов» В в пару «зрелых кроликов» А. Очевидно, что процесс «созревания» новорожденной пары В проходит промежуточные этапы, соответствующие каждому месяцу:

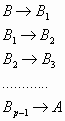(60)

Например, для случая р=2 процесс преобразования «новорожденнной пары» В в «зрелую пару» А реализуется в течение 2-х месяцев и описывается следующей системой переходов:

В ® В1;

(61)

В1 ® А.

(62)

Тогда, принимая во внимание переходы (57), (61), (62), процесс «размножения» для случая p=2 может быть представлен с помощью следующей Табл. 8.

Таблица 8

Заметим, что столбец А Табл. 8 задает число «зрелых пар» на каждой стадии размножения, столбец В задает число «новорожденных пар», столбец В₁ задает число «новоржденных пар», находящихся всостоянии В₁, столбец А+В+В₁ задает общее число кроличьих пар на каждой стадии размножения.

Анализ этих числовых последовательностей в каждом столбце

А: 1, 1, 1, 2, 3, 4, 6, 9, 13, 19,...

В: 0, 1, 1, 1, 2, 3, 4, 6, 9, 13,...

В₁: 0, 0, 1, 1, 1, 2, 3, 4, 6, 9, 13,...

А+В+ В₁: 1, 2, 3, 4, 6, 9, 13, 19,...

показывает, что все они подчиняются одной и той же закономерности: каждое число последовательности равно сумме предыдущего и отстоящего от него на 2 позициии. Но мы знаем, что 2-числа Фибоначчи, задаваемые рекуррентным соотношением (15), подчиняются этой же закономерности!

Если мы проведем подобные рассуждения для общего случая р мы прийдем к заключению, что p-числа Фибоначчи, задаваемые рекуррентным соотношением (20), являются решением обобщенного варианта задачи о размножении кроликов! И они являются количественным отражением общего «Принципа Асимметрии» живой природы, согласно которому размножение биологических объектов осуществляется согласно рекуррентному соотношению (20), задающему р-числа Фибоначчи!

На первый взгляд кажется, что сформулированная выше обобщенная задача о «размножении кроликов» не имеет никакого «физического» смысла. Однако результаты, изложенные в работе [30], показывают, что деление биологических клеток, действительно, подчиняется рекуррентному соотношению (20), то есть, деление биологических клеток осуществляется «по Фибоначчи»!

9. «Золотые» алгебраические уравнения

Издавна изучение многочленов и способов решения алгебраических уравнений привлекало особое внимание математиков, и эта важная математическая задача способствовала развитию алгебры. Обычно главный вопрос, который решается в теории алгебраических уравнений состоит в том, чтобы найти корни данного алгебраического уравнения. А теперь мы поставим другой вопрос. Нам известно простейшее алгебраическое уравнение (28), корнем которого является золотая пропорция. Поставим следующий вопрос: а существуют ли алгебраические уравнения более высоких степеней, корнем которых является золотая пропорция? И если да, то какую форму они имеют? Для ответа на этот вопрос проведем следующие рассуждения, взяв в качестве исходного уравнение золотой пропорции, задаваемое (28).

Умножим обе части уравнения (28) на x; в результате получим:

x3 = x2 + x.

(63)

Уравнения (28) можна переписать следующим образом:

x = x² –1.

Подставляя это значение для переменной x в выражение (63), получим следующее алгебраическое уравнение 3-й степени:

x3 = 2x2 – 1.

(64)

С другой стороны, если в выражение (63) подставить выражение для x², задаваемое (28), то получим еще одно уравнение 3-й степени:

x3 = 2x + 1.

(65)

Таким образом, мы получили два новых алгебраических уравнения 3-й степени, которые имеют общий корень – золотую пропорцию.

Выведем теперь выражение для «золотого» алгебраического уравнения 4-й степени. Для этого умножим все члены равенства (63) на x; в результате получим:

x4 = x3 + x2.

(66)

Затем мы можем воспользоваться выражением (28) для x², а также воспользоваться выражениями (64) или (65) для x³. Подставляя их в выражение (66), мы получим два новых алгебраических уравнения 4-й степени, корнями которых является золотая пропорция:

x4 = 3x2 — 1;

(67)

x4 = 3x + 2.

(68)

Анализ уравнения (68) приводит нас к неожиданному результату. Оказывается, что это уравнение описывает энергетическое состояние молекулы бутадиена – ценного химического вещества, которое используется при производстве каучука. Известный американский физик, Лауреат Нобелевской Премии Ричард Фейнман выразил свое восхищение по поводу уравнения (68) в следующих словах: «Какие чудеса существуют в математике! Согласно моей теории золотая пропорция древних греков дает минимальное энергетическое состояние молекулы бутадиена».

Этот факт сразу же повышает наш интерес к уравнениям золотой пропорции высших степеней, которые, возможно, описывают энергетические состояния других физических веществ. Эти уравнения могут быть получены, если мы будем последовательно рассматривать уравнения типа xⁿ = x^n-1+ x^n-2. В качестве примера можно вывести следующие «золотые» уравнения высших степеней:

Анализ этих уравнений показывает, что числовые коэффициенты в правой части этих уравнений есть ни что иное, числа Фибоначчи (9). Легко показать, что в общем случае алгебраические уравнения золотой пропорции n-й степени выражаются в следующем виде:

xn = Fnx2 - Fn-2 = Fnx + Fn-1,

(69)

где F_n, F_n-1 ,F_n-2 — числа Фибоначчи.

Заметим еще раз, что главным математическим свойством всех уравнений типа (69) является то, что все они имеют общий корень – золотую пропорцию.

Таким образом, наши достаточно элементарные рассуждения привели нас к небольшому математическому открытию: мы нашли бесконечное число новых алгебраических уравнений, задаваемых (69), корнем которых является золотая пропорция. Если теперь подставить вместо x в уравнение (69) его корень , то получим следующие замечательные тождества, связывающее золотую пропорцию с числами Фибоначчи:

t n = Fnt 2 - Fn-2 = Fnt + Fn-1.

(70)

Легко вычислить 18-е, 19-е и 20-е числа Фибоначчи:

F18 = 2584, F19 = 4181, F20 = 6765  .

(71)

Но тогда с учетом (71), используя (89), мы можем записать следующие «золотые» алгебраические уравнения 20-й степени:

x20 = 6765x2 – 2584

(72)

x20 = 6765x + 4181

(73)

Трудно вообразить, что корнем этих уравнений 20-й степени (72), (73) является золотая пропорция! Но это вытекает из рассмотренной выше теории алгебраических уравнений золотой пропорции, задаваемых (70). И глядя на уравнения (59), (72),(73), мы еще раз можем убедиться в величии математической науки, которая позволила нам в такой компактной форме выразить столь сложную научную информацию.

В работе [24] подобное исследование было проведено для «золотого» алгебраического уравнения (34), корнем которого является золотая р-пропорция t _р. При этом было найдено следующее общее «золотое» алгебраическое уравнение n-й степени:

(74)

где F_p(n) — р-числа Фибоначчи, задаваемые формулами (20), (21).

Из этого уравнения вытекает следующее тождество, которое связывает золотые р-пропорции t _рс р-числами Фибоначчи F_р(n):

(75)

Таким образом, основным результатом работы [24] является доказательство существования бесконечного числа алгебраических уравнений, корнями которых являются золотые р-пропорции. Эти «золотые» уравнения могут представлять фундаментальный интерес для теоретической физики, поскольку эти уравнения, возможно, выражают энергетические соотношения многих физических веществ. Для случая бутадиена этот факт был доказан выдающимся физиком Ричардом Фейнманом. И если это будет доказано, то это будет еще одним подтверждением, что в основе физических структур лежит Гармония!

10. Закон структурной гармонии систем

Исследования белорусского философа Эдуарда Сороко [31] имеют фундаментальное значение для развития современной науки и философии. Главная идея Сороко состоит в том, чтобы рассмотреть реальные системы с «диалектической точки зрения». Как известно, всякий объект природы может быть представлен как диалектическое единство двух противоположных сторон A и B. Это диалектическая связь может быть выражена в следующем виде:

A + B = U (universum). где А и В – стороны диалектического противоречия

(76)

Равенство (76) является наиболее общей формой выражения так называемого закона сохранения. Здесь А и В различия внутри единства, логически непересекающиеся классы или состояния субстрата некоторого целого. Единственное условие: А и В должны измеряться одной и той же мерой, быть членами отношения, лежащего внутри единства. Примерами (76) могут быть вероятность и невероятность событий, масса и энергия, ядро атома и его оболочка, вещество и поле, анод и катод, животные и растения, духовное и материальное начала в системе ценностей, доход и расход и т.д.

Выражение (76) может быть представлено в следующей нормализованной форме:

Aў + Bў = 1,

(77)

где Aў и Bў — относительные «веса» частей A и B, формирующих некоторое единство.

Частным случаем (77) является «закон сохранения информации»:

I + H = log N,

(78)

где I — количество информации и H — энтропия системы, имеющей N состояний.

В нормализованной форме закон (78) может быть представлен в следующей форме:

R + ` H = 1,

(79)

где

(80)

относительная избыточность, а

(81)

относительная энтропия.

Рассмотрим процесс самоорганизации системы. Он сводится к переходу системы в состояние гармонического равновесия. Можна высказать предположение, что для каждой самоогранизующейся системы существует некоторое соотношение, пропорция между сторонами A и B диалектического противоречия (76) в состоянии гармонического равновесия. Это соотношение имеет строго регулярный характер и является причиной стабильности системы.

Проведя ряд достаточно убедительных рассуждений, Эдуард Сороко пришел к выводу, что в состоянии «гармонического равновесия» между частями «диалектического противоречия» (76) в процессе самоорганизации устанавливается соотношение, равное величине, обратной золотой р-пропорции, то есть

где t _р – золотая р-пропорция.

На этом основании Эдуард Сороко формулирует «закон структурной гармонии систем», сущность которого сводится к следующему:

«Обобщенные золотые сечения суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоничное строение, стационарный режим существования, стуктурно-функциональную... устойчивость».

В чем же принципиальная особенность «Закона Сороко»? Начиная с Пифагора, ученые связывали понятие гармонии с единственной золотой пропорцией. «Закон Сороко» утверждает, что гармоничное состояние системы, соответствующее классической золотой пропорции, не является единственным и что для одной и той же системы может существовать бесконечное количество «гармоничных» состояний, соответствующих обобщенным золотым пропорциям t _р или обратным к ним числам b _р. Значения структурных инвариантов b _р для начальных значений р задаются с помощью следующей Табл. 9.

Таблица 9

Структурные инварианты самооргагизующихся систем

р	1	2	3	4	5	6	7
b р	0.6180	0.6823	0.7245	0.7549	0.7781	0.7965	0.8117

«Закон Сороко» имеет весьма интересные приложения к термодинамическим и информационным системам. Как известно, состояние термодинамической и информационной системы может быть выражено с помощью понятия энтропии, которое является важнейшим понятием в термодинамике и теории информации. Выражение для энтропии источника информации с алфавитом

имеет следующий вид:

(82)

где p₁, p₂,..., p_N — вероятности букв a₁, a₂,..., a_N; N — число букв в алфавите.

Как известно, энтропия (82) достигает своего максимального значения

Hmax = log N

(83)

для случая, когда вероятности букв равны между собой, то есть

Используя понятие относительной энтропии (81), мы можем записать следующее очевидное равенство:

(84)

В соответствии с «законом структурной гармонии систем» в состоянии «гаромонического» равновесия ее относительная энтропия (81) должна равняться одному из чисел b _р, задаваемых Табл.9. Тогда равенство (84) может быть записано в виде:

(85)

Ясно, что для заданного значения параметра р проблема получения множества значений вероятностей p_i (i = 1, 2,..., n) в выражении (85), дающих оптимальное значение энтропии H_opt, имеет много решений. Однако тем не менее соотношение (85) играет роль некоторой «целевой» функции для решения различных научных и технических проблем, потому что оно указывает путь поиска «оптимальных» вариантов.

Сороко приводит в своей книге «Структурная гармония систем» [31] ряд интересных примеров из различных областей науки, демонстрирующих действие своего закона. Например, рассмотрим такой объект как «сухой воздух», который является основой жизни на земле. Является ли структура воздуха оптимальной? Теория Сороко дает положительный ответ на это вопрос. Действительно, химический состав сухого воздуха таков: азот 78,084%; кислород — 20,947%; аргон — 0,934%; углекислый газ — 0,031%; неон — 0,002%; гелий — 0,001%. Если теперь рассчитать энтропию воздуха в соответствии с формулой (82) и вычислить его приведенную энтропию, разделив энтропию H на log N = log 6, то полученное значение приведенной энтропии будет равно 0,683, что с высокой точностью соответствует инварианту b ₂ = 0,0682. Это означает, что в процессе самоорганизации «сухой воздух» приобрел оптимальную, то есть «гармоничную» структуру. Этот пример является весьма показательным в том отношении, что «теория Сороко» может быть уже сейчас использована для контроля за состоянием биосферы, в частности, воздушного и водного бассейна. Ясно, что практическое использование «закона структурной гармонии систем» может принести существенный выигрыш при решении многих технологических, экономических, экологических и других задач, в частности, совершенствовать технологию изготовления структурно-сложных продуктов, контролировать биосферу и т.д.

11. Гиперболические функции Фибоначчи и Люка и новая геометрия живой природы

В работе [11] введен новый класс гиперболических функций – гиперболические функции Фибоначчи и Люка, которые задаются следующими выражениями:

Гиперболический синус и косинус Фибоначчи:

(86)

Гиперболический синус и косинус Люка:

,

(87)

где t = .

В работе [20] введены так называемые симметричные гиперболические функции Фибоначчи и Люка.

Симметричный гиперболический синус и косинус Фибоначчи:

;

(88)

Симметричный гиперболический синус и косинус Люка:

(89)

Как показано в работах [11, 15, 20], основной особеностью функций (86)-(89) является то, что при дискретных значениях переменной x, то есть, когда x принимает значение из множества {0, ±1, ±2, ±3, …}, гиперболические функции Фибоначчи и Люка совпадают с числами Фибоначчи и числами Люка соответственно.

Блестящим подтверждением эффективности примениния гиперболических функций Фибоначчи и Люка (86)-(87) для моделирования процессов, протекающих в живой природе, является новая геометрическая теория филллотаксиса, разработанная украинским архитектором Олегом Боднаром [32]. В этой работе доказано, что геометрия живой природы является неевклидовой, причем эта геометрия основана на новом классе гиперболических функций – гиперболических функциях Фибоначчи и Люка, основанных на золотой пропорции!

12. «Золотые» проекты или роль Математики Гармонии для развития современной науки

В статье «Fundamentals of new kind of mathematics based on the Golden Section» [25], которая является одной из важнейших цикла работ автора, посвященных изложению Математики Гармонии, изложена следующая иерархия математических концепций и теорий, входящих в состав «Математики Гармонии»:

Биномиальная теорема, биномиальные коэффициенты, треугольник Паскаля
→ Числа Фибоначчи, Золотое Сечение
→ Р-числа Фибоначчи и Золотые р-сечения
→ Обобщенный принцип Золотого Сечения
→ «Золотые» алгебраические уравнения, основанные на Золотых р-сечениях
→ Формулы Бине и гиперболические функции Фибоначчи и Люка
→ Теория формул Бине для р-чисел Фибоначчи и р-чисел Люка
→ Теория матриц Фибоначчи, основанная на р-числах Фибоначчи
→ Теория «золотых» матриц, основанная на гиперболических функциях Фибоначчи
→ Алгоритмичекая теория измерения
→ Р-коды Фибоначчи и коды Золотой р-пропорции
→ Новая теория действительных чисел
→ Новая компьютерная арифметика и компьютеры Фибоначчи
→ Новая теория кодирования и криптографии, основанная на матрицах Фибоначчи и «золотых» матрицах

В этой статье нет возможности углубляться в эту иерархию. Эта иерархия – скорее программа дальнейших исследований в этом направлении и план новой книги по Математике Гармонии, которая уже написана и 29-го мая 2003 г. представлена автором на семинаре «Геометрия и Физика» кафедры теоретической физики Московского университета (научный руководитель семинара проф. Ю.С. Владимиров).

Из этой иерархии вытекает, что Математика Гармонии, несомненно, является новой междисциплинарной теорией современной науки, которая может стать источником следующих «золотых» проектов современной науки и культуры:

1. Теория вероятностей. Невозможно переоценить методологическое значение глубокой математической связи обобщенных чисел Фибоначчи и «Обобщенного Принципа Золотого Сечения» с треугольником Паскаля и биномиальными коэффициентами. Ясно, что эта связь может стать началом переосмысливания многих разделов математики и теоретической физики, в которых комбинаторные соотношения играют определяющую роль, в частности, теории вероятностей и статистических законов.
2. Теория чисел. В работе [19] дано новое геометрическое определение числа, которое может стать начлом новой теории чисел. Этот научный результат имеет «стратегическое» значение для развития теории чисел, так приводит к бесконечному числу «конструктивных» теорий чисел, основанных на понятии золотой p-пропорции.
3. Теория измерения. Как известно, теория измерения, основанная на аксиомах Евдокса-Архимеда и Кантора, является одной из фундаментальных теорий математики. В этой связи алгоритмическпая теория измерения, изложенная автором в работах [6, 7, 9], имеет фундаментальный интерес для развития математики.
4. Теория систем счисления. Созданные в рамках Математики Гармонии системы счисления с иррациональными основаниями, основанные на золотых р-пропорциях, являются принципильно новым классом систем счисления, переворачивающим наши представления о теории систем счисления, которая является одной из наиболее древних математических теорий.
5. Теория элементарных функций. Гиперболические функции Фибоначчи и Люка, изложенные в [11, 15, 20], являются новым классом «элементарных функций», которые имеют такое же «стратегическое» значение для развития современной математики и теоретической физики, как широко известные всем тригонометрические и гиперболические функции. Можно ожидать появление следующих математических теорий «космологического» характера из этого подхода: (1) Геометрия Лобачевского-Фибоначчи как «фибоначчиева» интрепретация геометрии Лобачевского; (2) Геометрия Минковского-Фибоначчи как «фибоначчиева» интерпретация специальной теории относительности Эйнштейна.
6. Теория чисел Фибоначчи. Математика Гармонии создает новые стимулы для развития «теории чисел Фибоначчи» [28, 29]. Прежде всего, рекуррентная формула для р-чисел Фибоначчи, задаваемых (20), (21), значительно расширяет класс рекуррентных числовых рядов. С другой стороны, гиперболические функции Фибоначчи и Люка [11, 15, 20] превращают «теорию чисел Фибоначчи» в «непрерывную» теорию, что позволяет применить здесь математический аппарат «непрерывной» математики, в частности, дифференцирование и интегрирование.
7. Теория матриц. Матрицы Фибоначчи, описанные в [13], и «золотые» матрицы, описанные в [21], обладают уникальными математическими свойствами. Ясно, что изучение таких матриц и поиск новых их приложений в современной науке может стать интересным направлением в теории матриц.
8. Физика, кристалллография и астрономия. Работы [33-42] являются достаточно убедительным свидетельством повышенного интереса современной теоретической физики, кристаллографии и теоретической астрономии к Золотому Сечению. Работы Шехтмана, Бутусова, Mauldin и William, El Naschie, Владимирова, Петруненко и других физиков показывают, что невозможно вообразить дальнейшее развитие теоретической физики и космологических исследований без Золотого Сечения. Известный российский физик-теоретик проф. Владимиров Ю.С. заканчивает свою книгу «Метафизика» [40] следующими примечательными словами: «Таким образом, можна утверждать, что в теории слабых взаимодействий возникает соотношение Золотого Сечения, которое играет важную роль в различных сферах Науки и Искусства».
9. Философия. «Закон структурной гармонии систем», сформулированный белорусским философом Э.М. Сорокой [31], можно рассматривать как одно из значительных достижений современной философии. По существу, «Закон Сороки» является блестящим подтверждением эффективности приложения «Обобщенного Принципа Золотого Сечения» [21] к теории самоорганизующихся систем.
10. Ботаника. Новая геометрческая теория филлотаксиса, изложенная в книге [32] доктора искусствоведения, профессора Боднара О.Я. («Геометрия Боднара»), является блестящим подтверждением эффективности приложения гиперболических функций Фибоначчи и Люка [11, 15, 20] для моделирования явления филллотаксиса.
11. Биология. Деление клеток является одной из актуальных проблем биологии. В работе [30] доказано, что деление клеток является «асимметричным» и основано на p-числах Фибоначии (20), (21). Этот результат может стать началом математической теории деления биологических клеток.
12. Медицина. Российский биолог Виктор Цветков в своей книге «Сердце, Золотое Сечение и Симметрия» [42] показал, что сердечная деятельность млекопитающихся подчиняется закону Золотого Сечения.
13. Компьютеры. «Арифметика Фибоначчи» и «золотая» арифметика, изложенные автором в работах [6, 8, 14], могут стать началом новых компьютерных проектов. 65 зарубежных патентов, выданных патентыми ведомствами США, Японии, Англии, Германии, Франции, Канады и других стран, являются юридическими документами, подтверждающими приоритет советской науки (и приоритет автора настоящей статьи) в этой важной компьютерной области.
14. Измерительные системы. Новая теория измерения, цифровой метрологии и «золотых» резистивных делителей, изложенная в работах [6, 8], является теоретической основой для создания «золотых» аналого-цифровых и цифро-аналоговых преобразователей. Эффективность такого подхода подтверждена рядом инженерных разработок, выполненных под руководством автора. Разработанный еще в 80-е годы самокорректирующийся 18-разрядный АЦП для преобразования звуковых сигналов, на тот период являлся одной из лучших разработок в этой области не только в СССР, но и за рубежом.
15. Теория кодирования. В работах [18, 21] показано, что матрицы Фибоначчи и «золотые» матрицы являются математической основой новой теории кодирования, которая может эффективно использоваться для обнаружения и коррекции ошибок и криптографической защиты цифровых сигналов.
16. Музей Гармонии и Золотого Сечения [16] является уникальным научным, историческим, природным и художественным музеем, которому нет аналогов в мировой культуре. Музей представляет собой коллекцию всех созданий природы, науки и искусства, основанных на Золотом Сечении. В 2001 г. автор (совместно с Анной Слученковой) создал на Интернете сайт http://www.goldenmuseum.com/, в котором дано детальное обоснование этого уникального проекта.
17. Реформа математического образования на основе Золотого Сечения. Традиционно так называемая «Элементарная математика», созданная еще в античный период, лежит в основе программы математического образования в средней школе. К сожалению, роль Золотого Сечения в современном математическом образовании незаслуженно принижена по сравнению с той ролью, которую оно играло в греческой науке, науке эпохи Возрождения и последующие эпохи. В этой связи уместно напомнить следующее известное высказывание Иоганна Кеплера: «В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении (Золотое Сечение – А.С.). Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем». Анализ программ преподавания математики в школах России, Украины, Канады и других стран, показывает, что в этих программах нет даже упоминания о Золотом Сечении, то есть налицо сознательное игнорирование одного из крупнейших математических открытий античности. Результат известен: каждый школьник знает теорему Пифагора, но многие так называемые «образованные» люди имеют весьма смутное представление о Золотом Сечении, а тем более о его роли в развитии человеческой культуры. Но ведь Золотое Сечение могло бы стать своеобразной «связующей нитью» между Природой, Наукой и Искусством и соответствующими школьными дисциплинами. Поэтому Золотое Сечение должно быть более широко представлено в математическом и общем образовании. В этом и состоит идея «Реформы математического образования на основе Золотого Сечения», предложенной автором. Своими соображениями автор поделился с профессором Аланом Роджерсоном, который возглавляет Международный Проект «Математическое образование в 21-м веке». Проф. Роджерсон прислал автору весьма обнадеживающее письмо следующего содержания: «Дорогой Профессор Стахов! Я восхищен Вашей статьей, наполненной интереснейшей информацией, часть из которой мне неизвестна. Ваши идеи настолько глубоки, что их внедрение в школах – это следующий шаг в математическом образовании. Имеются ли преподаватели в Украине или где-либо, которые начали использовать Ваши идеи и Вашу научную программу? В наибольшей степени я был бы заинтересован в информации об их преподавательском опыте. С наилучшими пожеланиями – Алан Роджерсон». Ясно, что это письмо может стать «стартовой площадкой» для широкого обсуждения этого предложения в научной и педагогической общественности.
18. Наука о Гармонии Систем. Математика Гармонии является математической основой для развития Науки о Гармонии Систем [10], которая может стать главной интегрирующей наукой 21-го века, который, как известно, является «веком Гармонии».

Очевидно, что Математика Гармонии являются частью современной математики. Возникает вопрос: какую «экологическую нишу» в общей теории математики может заполнить Математика Гармонии? Как известно, математика условно может быть разбита на две части, «элементарную математику», в которой изучаются исходные, «элементарные», то есть, фундаментальные понятия математики, и «высшую математику», которая развивает и углубляет эти «элементарные понятия». Так случилось в истории математики, что не все фундаментальные математические открытия античной математики были в одинаковой степени использованы современной наукой. В частности, золотое сечение и связанные с ним числа Фибоначчи, были отнесены «материалистической наукой» к разряду «сомнительных научных концепций» или «числовых курьезов», не связанных с общей теорией. И хотя в 19 в. французскими математиками Бине и Люка, а затем в 20 в. российским математиком Николаем Воробьевым и американским математиком Вернером Хоггатом, создателем Фибоначчи-Ассоциации, были предприняты энергичные попытки исправить эту историческую ошибку, отношение к золотому сечению и числам Фибоначчи в современной математике и математическом образовании остается прежним. Математика Гармонии является развитием и обобщением тысячелетних исследований в области теории золотого сечения, которая начала создаваться еще в Древней Греции. Ее главная цель – ввести в современную науку золотое сечение и числа Фибоначчи в качестве фундаментальных понятий современной науки. Таким образом, Математика Гармонии как бы заполняет «экологическцю нишу» между «элементарной математикой», основная часть которой была создана еще в античной науке, и совремнной «высшей математикой». Использование Математики Гармонии в современной математике, теоретической физике и компьютерной науке может оказаться весьма плодотворным направлением современных теоретических исследований.

Литература

1. Клайн М. Математика. Утрата определенности (пер. с англ.). Москва, Мир, 1984 / 434 c.
   
2. Кондратьев В.Г., Солодухина М.А. Мягкое исчисление как новая парадигма. Обзор // РЖ, сер.3, философия, 2000, №3, c.34-41.
   
3. Арнольд В.И. «Жёсткие» и «мягкие» математические модели. Природа, 1998, №4, c.3-14.
   
4. Панов М.И. Гуманитаризация математики – тенденция развития науки XX века: (можно ли считать математику сплавом культуры, философии, религии?). Обзор // РЖ, сер.3, философия, 1991, №6, c.21-30.
   
5. Шевелев И.Ш. Метаязык живой природы, Кострома, Изд-во «Воскресенье», 2000 / 352 c.
   
6. Стахов А.П. Введение в алгоритмическую теорию измерения. Москва, Советское радио, 1977 / 288 c.
   
7. Стахов А.П. Алгоритмическая теория измерения. Москва, Знание, 1979 / 64 c.
   
8. Стахов A.П. Коды золотой пропорции, Москва, Радио и связь, 1984 / 152 c.
   
9. Stakhov A.P. The Golden Section in the measurement theory. An International Journal «Computers & Mathematics with Applications», Volume 17, No 4-6, 1989, 613-638.
   
10. Стахов О.П. Золотий переріз і наука про гармонію систем. Київ, Вісник Академії наук Української РСР, 1991, №12, с. 8-15.
    
11. Стахов А.П., Ткаченко И.С. Гиперболическая тригонометрия Фибоначчи. Киев, Доклады Академии наук Украины, 1993, том 208, № 7, с. 9-14.
    
12. Stakhov, A.P. The Golden Section and Modern Harmony Mathematics, Applications of Fibonacci Numbers, Vol. 7, Kluwer Academic Publishers, 1998, 393-399.
    
13. Stakhov A.P. A generalization of the Fibonacci Q-matrix, Киев, Доклады Академии наук Украины, 1999, No 9, с. 46-49.
    
14. Stakhov, A.P. Brousentsov’s Ternary Principle, Bergman’s Number System and Ternary Mirror-symmetrical Arithmetic, The Computer Journal (British Computer Society), 2002, Vol. 45, No. 2, p. 222-236.
    
15. Stakhov A.P. Hyperbolic Fibonacci and Lucas Functions: A New Mathematics for Living Nature. Винница, Изд-во «ITI», 2003 / 240 c.
    
16. Stakhov A.P., Sluchenkova A.A. Museum of Harmony and the Golden Section: Mathematical connections in Nature, Science and Art. Vinnitsa, ITI, 2003 / 92 p.
    
17. Стахов А.П. Сакральная геометрия и математика гармонии. Труды Международной конференции «Проблемы гармонии, симметрии и Золотого Сечения в природе, науке и искусстве», Винница, Изд-во Винницкого госудврственного аграрного университета, 2003, с. 8-
    
18. Стахов А.П. Кодирование данных, основанное на фибоначчиевых матрицах. Труды Международной конференции «Проблемы гармонии, симметрии и Золотого Сечения в природе, науке и искусстве», Винница, Изд-во Винницкого госудврственного аграрного университета, 2003, с. 311-325.
    
19. Стахов A.П. Обобщенные Золотые Сечения и новый подход к геометрическому определению числа, Киев, Украинский математический журнал, 2004, Vol. 56, No 8, с. 1143-1150
    
20. Stakhov A., Rozin B. On a new class of hyperbolic function — Chaos, Solitons & Fractals, 2005, V. 23, No.2, р. 379-389.
    
21. Stakhov A. The Generalized Principle of the Golden Section and its Applications in Mathematics, Science and Engineering. — Chaos, Solitons & Fractals, 2005, V. 26, No.2, р. 263-289.
    
22. Stakhov A., Rozin B. The Golden Shofar — Chaos, Solitons & Fractals Chaos, Solitons & Fractals, 2005, V. 26, No.3, р. 677-684.
    
23. Stakhov A., Rozin B. Theory of Binet formulas for Fibonacci and Lucas p-numbers — Chaos, Solitons & Fractals (2005, in publication).
    
24. Stakhov A., Rozin B. The «Golden» Algebraic Equations — Chaos, Solitons & Fractals (2005, in publication).
    
25. Stakhov A., Fundamentals of a new kind of Mathematics based on the Golden Section — Chaos, Solitons & Fractals (2005, in publication).
    
26. Неаполитанский С.М., Матвеев С.А. Сакральная геометрия. Санкт-Петербург, Изд-во «Святослав», 2003 / 632 c.
    
27. Bergman, G. A. A number system with an irrational base. USA, Mathematics Magazine, 1957, No.31, p. 98-119.
    
28. Воробьев Н.Н. Числа Фибоначчи, Москва, Наука, 1969 / 112 c.
    
29. Hoggat, V. E. Fibonacci and Lucas Numbers, Houghton-Mifflin, Palo Alto, California, 1969.
    
30. Spears C.P., Bicknell-Johnson M. Asymmetric cell division: binomial identities for age analysis of mortal vs. immortal trees, Applications of Fibonacci Numbers, Vol. 7, 1998, p. 377-391.
    
31. Сороко Э.М. Структурная гармония систем. Минск, Наука и техника, 1984 / 264 c.
    
32. Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. Львов, Изд-во «Свит», 1994 / 204 c.
    
33. Гратиа Д. Квазикристаллы. Москва, Успехи физических наук., 1988, том 156, вып. 2, с. 347-363
    
34. Бутусов К.П. Золотое сечение в Солнечной системе. Москва, Астрономия и небесная механика. Серия «Проблемы исследования Вселенной», 1978, вып. 7, с. 477-500.
    
35. Mauldin R.D. and Willams S.C. Random recursive construction. Trans. Am. Math. Soc. 1986; 295, р. 325-346.
    
36. El Naschie M.S. On dimensions of Cantor set related systems. Chaos, Solitons & Fractals, 1993, 3, р. 675-685.
    
37. El Nashie M.S. Is Quantum Space a Random Cantor Set with a Golden Mean Dimension at the Core? Chaos, Solitons & Fractals, 1994; 4(2); 177-179.
    
38. El Naschie M.S. On a class of general theories for high energy particle physics. Chaos, Solitons & Fractals, 2002, 14, р. 649-668.
    
39. Владимиров Ю.С. Кварковый икосаэдр, заряды и угол Вайнберга. Труды Международной конференции «Проблемы гармонии, симметрии и Золотого Сечения в природе, науке и искусстве», Винница, Изд-во Винницкого госудврственного аграрного университета, 2003, с. 69-79.
    
40. Владимиров Ю.С. Метафизика. Москва, Бином, 2002 / 550 c.
    
41. Петруненко В.В. К вопросу о физической сущности явления декалогарифмической периодичности. Труды Международной конференции «Проблемы гармонии, симметрии и Золотого Сечения в природе, науке и искусстве», Винница, Изд-во Винницкого госудврственного аграрного университета, 2003, с. 80-86.
    
42. Майборода А.О. Открытие Golden Section в фундаментальных соотношениях физических величин. Труды Международной конференции «Проблемы гармонии, симметрии и Золотого Сечения в природе, науке и искусстве», Винница, Изд-во Винницкого госудврственного аграрного университета, 2003, с. 87-94.
    
43. Цветков В.Д. Сердце, золотое сечение и симметрия. Пущино, Институт теоретической и экспериментальной биофизики, 1997 / 170 c.
    

[Обсуждение на форуме «Наука»]