Конструктивный подход к измерению

А теперь еще раз обратимся к «основному уравнению измерения»:

Q = qV,

(1)

где V — единица измерения, Q - измеряемая величина, q - измеряющее ее число.

Идея его доказательства состоит в следующем. С помощью аксиомы Евдокса-Архимеда из единицы измерения V по определенным правилам, называемым алгоритмом измерения, формируется некоторая последовательность «стягивающихся» отрезков, которые сравниваются с измеряемым отрезком Q; при устремлении этого процесса в бесконечность на основании аксиомы Кантора для любого Q при заданном V всегда найдется такой измеряющий Q отрезок, сформированный из V, который «абсолютно точно» совпадет с Q. Наиболее существенным в этом доказательстве является вытекающее из аксиомы Кантора представление об измерении, как о процессе, завершающемся за бесконечное время.

Однако выше было показано, что понятие «актуальной бесконечности» должно быть исключено из рассмотрения при создании «конструктивной» теории измерения в силу его внутренней противоречивости («завершенная бесконечность»).

Идеи современных математиков-конструктивистов, восходящие к знаменитому заявлению Гаусса: «Я возражаю … против употребления бесконечной величины как чего-либо завершенного, что никогда не позволительно в математике: можно лишь говорить о пределах, к которым некоторые величины приближаются как угодно близко, или о неограниченно возрастающих величинах», — приводят к мысли о возможности построения математической теории измерения на основе интуитивной, «практической» идеи о конечности измерительного процесса, согласно которой всякое измерение завершается за конечное число шагов, и конструктивной идеи потенциальной осуществимости, в соответствии с которой мы отвлекаемся от ограниченности наших возможностей в выборе средств и количества измерительных шагов (т.е. количество измерительных шагов может быть установлено как угодно большим и всегда существует потенциальная возможность для совершения следующего шага измерения).

Такое, на первый взгляд, незначительное изменение в подходе приводит к переосмысливанию самих задач математической теории измерения. При теоретико-множественном подходе измерение ведется «до точки», т.е. до абсолютно точного совпадения измеряемого и измеряющего отрезков (возможность такого абсолютно точного измерения вытекает из аксиомы Кантора). При конструктивном подходе измерение никогда не доходит «до точки», а результатом измерения всегда является некоторый отрезок, некоторый интервал неопределенности относительно истинного значения измеряемой величины. С увеличением числа шагов измерения этот интервал сужается и может быть сделан как угодно малым, но никогда этот интервал не превращается в точку.

В своей известной работе «О философии математики» Герман Вейль следующим образом выражает различие между классическим и конструктивным представлениями о континууме: «Современному анализу континуум представляется в виде множества его точек, в континууме он видит лишь частный случай основного логического отношения элемента и множества. Но поразительно, что столь же фундаментальное отношение целого и части до сих пор не находило себе места в математике! Между тем обладание частями есть основное свойство континуума и брауеровская теория … кладет это отношение в основание математического изучения континуума. В этом заключается собственно основание сделанной выше … попытки исходить не из точки, а из интервалов, как из первичных элементов построения».

Одним из моментов в теоретико-множественной теории измерения является выбор способа или алгоритма измерения, задающего систему счисления, в которой нумеруется число (результат измерения). При бесконечном числе шагов измерения, т.е. при измерении «до точки», алгоритм не влияет на конечный результат измерения и поэтому проблема способов, алгоритмов измерения как серьезная математическая проблема здесь не возникает. Выбор алгоритма в значительной степени носит произвольный характер и, как правило, сводится к десятичному или двоичному алгоритму.

При конечном числе шагов измерения, т.е. при измерения «до интервала», между алгоритмами измерения появляется различие в достигаемой с их помощью «точности» измерения, под которой в данном случае понимается отношение исходного интервала неопределенности к интервалу неопределенности на последнем, завершающем шаге измерения. При таких условиях вступает в действие вторая конструктивная идея об «эффективности» алгоритмов измерения, а задача синтеза «эффективных» или «оптимальных» алгоритмов измерения и выдвигается в качестве центральной задачи конструктивной (алгоритмической) теории измерения.

Принцип асимметрии измерения

Подытоживая свой научный путь, каждый ученый стремится выделить те наиболее существенные научные идеи и предложения, которые ему удалось сформулировать и развить. Моим первым оригинальным математическим результатом была «алгоритмическая теория измерения», восходящая к «задаче о гирях», которая впервые была сформулирована Фибоначчи еще в 13-м веке. Что же нового я внес в эту задачу? Я полагаю, что основной «изюминкой» алгоритмической теории измерения является так называемый «принцип асимметрии измерения».

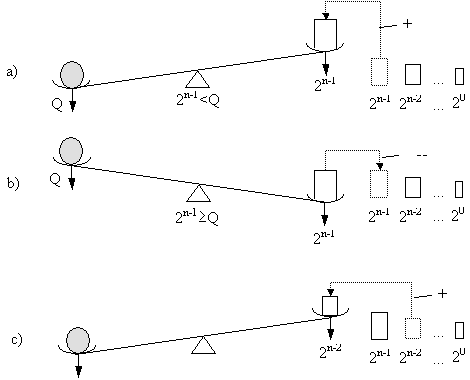
Принцип асимметрии измерения

Для пояснения этой идеи обратимся снова к упоминавшейся выше задаче о взвешивания неизвестного груза Q с помощью рычажных весов. Пусть «весовщик» использует для взвешивания «двоичную» систему, состоящую из n гирь, записанных в порядке старшинства: 2^n-1, 2^n-2, …, 2¹, 2⁰. Тогда сам процесс измерения реализуется путем сравнения «весовых гирь» с измеряемым грузом Q, что осуществляется с помощью рычажных весов. При этом «весовщик» наблюдает за состоянием или положением, в котором оказываются рычажные весы после очередного сравнения, и в зависимости от этого принимает решение о своих действиях на очередном шаге сравнения.

Будем считать, что рычажные весы могут находиться только в двух положениях: (а) «больше», когда измеряемый груз перевешивает гири и (б) «меньше» — в противоположном случае.

Первый шаг «двоичного» алгоритма измерения состоит в том, что «старшая» гиря 2^n-1, кладется на свободную чашу весов. При этом в зависимости от соотношения весов груза Q и гири 2^n-1 рычажные весы после первого шага сравнения могут оказаться в положении «больше», если 2^n-1< Q (то есть весы остаются в том же положении, что и до сравнения) или в положении «меньше», если 2^n-1і Q (в последнем случае рычажные весы переходят в противоположное положение).

При этом оказывается, что действия «весовщика» после сравнения в первом и во втором случае существенно различаются. Действительно, в первом случае следующий шаг состоит в добавлении на правую чашу весов очередной по старшинству гири 2^n-2. Во втором случае «весовщик» должен выполнить две операции: снять предыдущую гирю, после чего рычажные весы возвращаются в исходное положение, а затем добавить на правую чашу весов следующую гирю.

Таким образом, логика любого измерения, осуществляемого с помощью рычажных весов, «несимметрична» в том смысле, что предполагает различную степень сложности действий «весовщика» в зависимости от результата предыдущего сравнения; причем действия «весовщика» после получения сигнала «меньше» (правая чаша перевесила) оказываются сложнее по сравнению с его действиями после получения сигнала «больше» (весы остались в исходном положении).

Обнаруженное свойство измерения я назвал «принципом асимметрии измерения». Этот принцип накладывает определенные ограничения на измерение, которые должны быть учтены в его алгоритме.

Для строгой формулировки нового варианта «задачи о гирях» (с учетом «принципа асимметрии измерения») рассмотрим измерение как процесс, протекающий в дискретные моменты времени, и пусть операция «добавить гирю» (+) выполняется за одну единицу дискретного времени, а операция «снять гирю» (-), после которой происходит возврат рычажных весов в исходное положение, — за р единиц дискретного времени, где р может принимать значения из следующего множества {0, 1, 2, 3, …, Ґ }. Параметр р мы будем называть «инерционностью» рычажных весов.

Ясно, что значение р=0 соответствует классическому варианту «задачи о гирях», когда мы в своих рассуждениях пренебрегаем «асимметрией» сравнения. При других значениях р мы получаем различные варианты задачи о гирях, при решении которых должна учитываться «инерционность» р.

«Фибоначчиевые» алгоритмы измерения

Как упоминалось выше, оптимальным решением «задачи о гирях», когда гири разрешается класть только на свободную чашу весов, является двоичная система гирь:

{20, 21, 22, …, 2n-1}.

(1)

При этом «оптимальный» алгоритм измерения, называемый «двоичным» алгоритмом, состоит в последовательном сравнении измеряемого веса Q с «двоичными» гирями (1), начиная со старшей гири 2^n-1. Заметим, что применение «двоичного» алгоритма автоматически приводит к представлению результата измерения N в «двоичной» системе счисления:

N = an2n-1 + an-12n-2 +... + ai2i-1 +... + a120.

(1)

где двоичные коэффициенты a_n, a_n-1,..., a_i, …, a₁, являющиеся битами двоичного представления (1), имеют очень простую «измерительную» интерпретацию: двоичная цифра a_i принимается равной 0, если при сравнении измеряемого веса с гирей 2^i-1 рычажные весы перешли в противоположное положение, или 1 – в противоположном случае.

Таким образом, изучая алгоритмы измерения, мы перешли к системам счисления. Оказывается, что каждый алгоритм измерения есть ни что иное как некоторый способ позиционного представления чисел.

Каким же будет оптимальное решение «задачи о гирях», если исходить из «Принципа асимметрии измерения»? И вот здесь нас с Игорем Витенько ждал сюрприз! Если задаться «инерционностью» рычажных весов р (р=0, 1, 2, 3, ….) и попытаться решить «задачу о гирях» в новой формулировке, то оптимальным решением является система гирь, которая задается с помощью р-чисел Фибоначчи, которые мы обнаружили при исследовании треугольника Паскаля, то есть «оптимальным» является следующий набор гирь:

{Fp(1), Fp(2), Fp(3), …, Fp(i), …, Fp(n)},

(2)

где F_p(i) – р-число Фибоначчи, задаваемое рекуррентным соотношением:

Fp(n) = Fp(n-1)+Fp(n-p-1)

(3)

при следующих начальных условиях:

Fp(1) = Fp(2) =... = Fp(p+1) = 1

(4)

Полученные при этом «оптимальные» алгоритмы, которые я назвал «фибоначчиевыми» алгоритмами, имеют следующую числовую интерпретацию:

N = anFp(n) + an-1Fp(n-1) +... + aiFp(i) +... + a1Fp(1),

(5)

где a_iО {0, 1} – двоичная цифра i-го разряда кода (5); n – разрядность кода (5); F_p(i) – вес is the i-го разряда, вычисляемый в соответствии с рекуррентным соотношением (3), (4). Позиционное представление натурального числа N в виде (5) я назвал р-кодом Фибоначчи числа N. Сокращенная запись суммы (5) имеет следующий вид:

N = an an-1... a1.

(6)

Заметим, что понятие p-кода Фибоначчи включает в себя бесконечное число различных методов позиционного представления, потому что каждое p «порождает» свой собственный p-код Фибоначчи (p = 0, 1, 2, 3,...).

Пусть p = 0. Для этого случая 0-числа Фибоначчи F₀(i) совпадают с «двоичными» числами, то есть

F₀(i) = 2^i-1.

Представление (5) для этого случая принимает форму «двоичного» представления (1).

Пусть p = Ґ. В этом случае p-числа Фибоначчи равны 1, то есть мы имеем для любого i:

F_p(i) = 1.

Тогда представление (5) принимает следующий вид:

(7)

Таким образом p-коды Фибоначчи являются весьма широким обобщением «двоичного» кода (1) и включают его в качестве частного случая, соответствующего p = 0. С другой стороны, p-коды Фибоначчи включают в себя так называемый «унитарный» код (7), соответствующий другому крайнему значению p = Ґ.

Как получить, например, «фибоначчиевое» представление некоторого натурального числа, например числа 30. Для этого запишем числа Фибоначчи в обратном порядке:

34, 21, 13, 8, 5, 3, 2, 1, 1.

Тогда мы должны сравнивать последовательно число 30 с числами Фибоначчи, начиная со старшего. Процесс формирования кода Фибоначчи демонстрируется с помощью следующей таблицы.

Сравним число 30 с числом Фибоначчи 34; так как 30<34, мы записываем 0 во второй строке и втором столбце таблицы. Затем мы сравниваем число 30 со следующим числом Фибоначчи 21. Так как 30і 21, мы записываем 1 во второй строке под числом 21. После этого мы образуем разность 30-21=9 и затем сравниваем число 9 со следующими числами Фибоначчи 13, 8, …, 2, 1, 1. В результате этой процедуры мы получаем следующее «фибоначчиевое» представление числа 30:

30 = 0 1 0 1 0 0 0 1 0.

Это позиционное представление есть ни что иное, как сокращенная запись следующей суммы:

30 = 21 + 8 + 1.

Таким образом, «алгоритмическая теория измерения» привела нас к небольшому математическому открытию в области теории систем счисления. Мы получили обобщение «двоичной» системы счисления! Благодаря этому открытию мы теперь знаем, что существует бесконечное число «двоичных» позиционных представлений, которые задаются некоторой общей формулой (5)! И классическая «двоичная» система счисления (1) является всего лишь частным случаем «фибоначчиевого» представления (5).

Но «двоичная» система счисления (1) является основой современных компьютеров! Но тогда возникает вопрос: если мы будем использовать «фибоначчиевые» представления (5) в компьютерах, то возможно мы сможем прийти к новым компьютерам, компьютерам Фибоначчи, как нового направления в развитии компьютерной техники!

Кроме «фибоначчиевых» алгоритмов измерения в алгоритмической теории измерения было получено много других неожиданных научных результатов, например, «биномиальные» алгоритмы измерения. Но меня увлекла прежде всего формула (5), которая открывала путь к новым компьютерам, компьютерам Фибоначчи.

Сейчас некоторые ученые пытаются опровергнуть мой приоритет в открытии р-чисел Фибоначчи. Для этого делаются ссылки на книгу знаменитого математика Д. Пойа «Математическое открытие», опубликованной на русском языке в 1970 г. (первое английское издание вышло в 1962 г.). Действительно, в упомянутой выше книге Пойа на с. 113-114 приведено упражнение с так называемыми «диагональными суммами» треугольником Паскаля, которое может привести к р-числам Фибоначчи, задаваемым (3), (4). Пойа предложил читателям в виде упражнения вывести эти числовые ряды, но общей формулы (3), задающей р-числа Фибоначчи в книге Пойа нет! Второе. Мы с Игорем Витенько пришли к р-числам Фибоначчи, решая задачу синтеза оптимальных алгоритмов измерения, к которой Пойа никакого отношения не имеет! Впервые этот результат был изложен нами в докладе «оптимальные алгоритмы функционирования преобразователей «напряжение-код», сделанном на V-й научно-технической конференции «Кибернетические пути совершенствования измерительной аппаратуры» (Ленинград, 1966 г.). На основе этого доклада мною с Витенько была подготовлена статья «Теория оптимальных алгоритмов аналого-цифрового преобразования», опубликованная в книге «Приборы и системы автоматики» (Харьков, изд-во Харьковского университета, 1970 г.).

Таким образом, знаменитый математик Пойа в свое книге «Математическое открытие» (1962 г.) наметил путь, с помощью которого можно прийти к р-числам Фибоначчи, но в своей книге он не вывел общей рекуррентной формулы (3), задающей р-числа Фибоначчи. Мы с Витенько пришли к этой формуле в 1966 г., решая задачу синтеза оптимальных алгоритмов измерения. Позже в своей книге «Введение в алгоритмическую теорию измерения» (1977), которая опубликована после трагической гибели Игоря Витенько (1974 г.), я показал связь р-чисел Фибоначчи с Треугольником Паскаля, то есть решил то упражнение, которое в своей книге сформулировал Пойа. А теперь сами судите, кто и когда ввел в науку р-числа Фибоначчи!