Что же это за «чудо» природы и математики, интерес к которому не только не увядает с течением времени, а наоборот – возрастает с каждым столетием. Для ответа на этот вопрос я еще раз обращаюсь к моему читателю вспомнить все свои математические знания, полученные им в средней школе (большего не требуется), и погрузиться в мир математики — только таким путем вы сможете насладиться чудесными математическими свойствами золотой пропорции и через эти математические свойства понять и оценить всю красоту и гармонию золотой пропорции t = » 1,618.

Начнем с алгебраических свойств «золотой пропорции». Из уравнения «золотой пропорции»

x2 = x + 1

(1)

непосредственно вытекает первое очень простое и тем не менее весьма удивительное свойство золотой пропорции. Если корень t («золотая пропорция») подставить вместо x в уравнение (1), то мы получим следующее тождество для «золотой пропорции»:

t 2 = t + 1.

(2)

Убедимся, что тождество (2) является истинным. Для этого нам необходимо осуществить элементарные математические преобразования над левой и правой частями тождества (2) и доказать, что они совпадают.

Действительно, мы имеем для правой части:

t + 1 = + 1 = .

С другой стороны,

t ² = = ,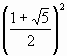

откуда вытекает справедливость тождества (2).

Тождество (2) может быть представлено в виде:

;

(3-a)

или

(3-b)

Проанализируем, например, тождество (3-b). Известно, что любое число а имеет обратное к нему число 1/а. Например, дробь 0,1 является числом, обратным к 10. Традиционный алгоритм получения обратного числа 1/а из исходного числа а состоит в делении числа 1 на число а. Это довольно сложная процедура. Попробуйте, например, путем деления получить число, обратное к числу а = 357821,093572. Это можно сделать только с помощью современного компьютера.

Рассмотрим теперь «золотую пропорцию» t = . Как получить из нее обратное число 1/t ? Выражение (3-b) дает очень простой ответ на этот вопрос. Для этого достаточно вычесть единицу из «золотой пропорции» t. Действительно, с одной стороны,

.

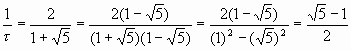С другой стороны, как следует из (3-b), «обратное» число 1/t может быть получено из t следующим путем:

Докажем теперь еще одно удивительное свойство «золотой пропорции», основываясь на тождестве (3-а). Если в правую часть (3-а) вместо t подставить его значение, задаваемое (3-а), то мы придем к представлению t в виде следующей «многоэтажной» дроби:

.

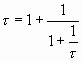Если продолжить такую подстановку в правой части бесконечное число раз, то в результате получим «многоэтажную» дробь с бесконечным количеством «этажей»:

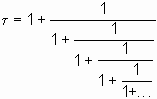(4)

Представление (4) в математике называется «непрерывной» или «цепной» дробью. Заметим, что теория «цепных» дробей является одной из важных частей современной математики.

Рассмотрим теперь еще раз тождество (2). Оно может быть представлено в следующей форме:

(5)

Если теперь в правой части тождества (5) вместо t подставить его выражение, задаваемое (5), то получим следующее представление t:

(6)

Если в правой части тождества (6) опять подставлять выражение (5) вместо t и повторить эту операцию бесконечное число раз, то мы получим еще одно «замечательное представление» золотой пропорции в «радикалах»:

.

(7)

Умножим вначале обе части члены тождества (2) на «золотую пропорцию» t, а затем разделим их на t. В результате получим два новых тождества:

t 3 = t 2 + t

(8)

и

Если теперь продолжать умножать тождество (8) на t , а тождество (9) делить на t и устремить этот процесс до бесконечности, то мы приходим к следующему изящному тождеству, связывающему степени «золотой пропорции»:

t n = t n-1 + t n-2,

(10)

где число n является целым и пробегает значения от +Ґ до -Ґ, то есть n = 0, ± 1, ± 2, ± 3, ….

Тождество (10) словесно можно выразить следующим образом: «Любая целая степень «золотой пропорции» равна сумме двух предыдущих».

Это свойство «золотой пропорции» является воистину «уникальным»! Действительно, очень трудно представить, что следующее тождество является «абсолютно верным»:

,

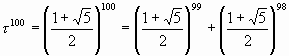(11)

но его справедливость однозначно вытекает из справедливости тождества (8).

Более того. Абсолютно верным является также следующее тождество:

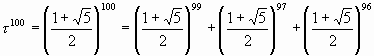
и подобных численных тождеств для числа t ¹⁰⁰ существует бесконечное количество, что также вытекает из тождества (8).

Рассмотрим последовательность степеней «золотой пропорции», то есть

…{... t -n, t -(n-1), …, t -2, t -1,t 0 = 1, t 1, t 2, …, t n-1, t n, …}.

(12)

Последовательность (12) обладает весьма интересным математическим свойством. С одной стороны, последовательность (12) является «геометрической прогрессией», в которой каждое число равно предыдущему, умноженному на постоянное для данной прогрессии число t , называемое знаменателем геометрической прогрессии, то есть:

t n = t ґ t n-1

(13)

С другой стороны, в соответствии с (8) последовательность (12) является «арифметическим рядом», так как каждое число есть сумма двух предыдущих. Заметим, что свойство (8) характерно только для геометрической прогрессии со знаменателем t и такая геометрическая прогрессия называется «золотой» прогрессией.

Поскольку каждой геометрической прогрессии типа (13) в геометрии соответствует некоторая логарифмическая спираль, то, по мнению многих исследователей, свойство (8), присущее только «золотой» прогрессии, является причиной широкого распространения именно «золотой» логарифмической спирали в формах и структурах живой природы. Но об этом мы поговорим позже, когда будем рассматривать «золотые» спирали.

В заключение отметим, что каждый математик интуитивно стремится выразить свои математические результаты в наиболее простой, компактной форме. И если такую форму удается найти, то это доставляет математику «эстетическое наслаждение». В этом отношении (стремление к «эстетическому» выражению математических результатов) математическое творчество подобно творчеству композитора или поэта, главной задачей которых состоит в получении совершенных музыкальных или поэтических форм, доставляющих «эстетическое удовольствие». Заметим, что формулы (4), (7) и (10) вызывают также «эстетическое наслаждение» и вызывают неосознанное чувство ритма и гармонии, когда мы начинаем задумываться над бесконечной повторяемостью одних и тех же простых математических элементов в формулах для t, задаваемых (4), (7) или (10).