Аннотация. Вопрос о возможности представления натурального числа в виде сумм чисел последовательности Фибоначчи возник, как один из вариантов, в связи с созданием Фибоначчи-компьютера. Это в определенном смысле, является в последнее время особенно актуальным и интересным для математиков и для кибернетиков, создающих устройства преобразования сигналов. Провести исследование в этом направлении на основе свойств функций Фибоначчи и функций Люка возникло у нас еще в прошлом веке. Полученные результаты представлены в работе [1], а с учетом последних усовершенствований представляем их вниманию читателей в таком вот варианте.

Введение. В статье «Фибоначчиева система счисления» [Wikipedia.org] утверждается, что «Прямой связи между представлением натуральных чисел в системе золотого сечения и в Фибоначчиевой не имеется». Вместе с этим отметим, что Д. Бергман в 1957 году предпринял попытку представить натуральное число через систему счисления с иррациональным основанием ( ф = 1,618033989…. — число Фидия)[goldenmuseum.com]. К этому же добавим, что согласно теореме Zeckendorf [Wikipedia.org/…/Zeckendorf’s theorem] для натурального числа N существует сумма чисел Фибоначчи.

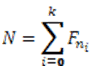           (1)

где Fn_i — есть n_i-е число Фибоначчи, и при этом

n_i ≥ 2 , n_i+1 > n_i + 1 , то есть в (1) не включается два последовательных числа.

Указывается также, что теорема состоит из двух частей:

1. Существование: каждое натуральное число N имеет представление Zeckendorf (1).

2. Уникальность: нет натурального N, которое имеет два различных представления Zeckendorf (1).

При представлении числа N, удовлетворяющего условиям теоремы, используется так называемый «жадный алгоритм».

Цель исследования. Проанализировав свойства последовательностей чисел Фибоначчи и чисел Люка, нами были введены соответствующие им функции [1, 2] по аналогии с гиперболическими функциями, которые моделируют при целочисленных значениях t, разбиение их на две пары последовательностей (табл. 1).

формате PDF (391Кб)