1. Еще раз о новом взгляде на «Начала» Евклида, основанном на «гипотезе Прокла»

Главная идея статьи Дениса Клещева «О былых и грядущих богах, жрецах и пророках науки» [1] состоит в том, что процессы научных парадигм в математике и физике тесно взаимосвязаны: вслед за сменой парадигмы в математике следует смена парадигмы в физике:

«Итак, мы подошли к самому интересному. Как видно из схемы внешней структуры научных революций, смена парадигмы в математике предшествует парадигмальному скачку в физике, эта историческая закономерность опровергает сложившийся в наши дни стереотип, что математика и физика методологически между собой не связаны. Такая связь существует, и далеко не случайно после монографии по истории математики «Математика. Утрата определенности» Моррис Клайн написал другую книгу «Математика. Поиск истины», посвященную аналогичному процессу утраты определенности в физике.

Распределение парадигмальных скачков, выделенных для наглядности в качестве точек спирали, обнаруживает чередование в ходе развития фундаментальной науки представлений о потенциальной и актуальной бесконечности, об ограниченной и неограниченной вселенной. При условии, что человеческая цивилизация будет продолжать развиваться дальше, следующий скачек из схемы, выведенной по теории Томаса Куна, следует ожидать в математике. По диалектическому принципу отрицания отрицания эта математическая парадигма призвана опровергнуть концепцию актуальной бесконечности. На это указывает близость точки G к точке C, под которой нами была обозначена Эпоха Платона и Аристотеля, когда актуальная бесконечность была отброшена как внутренне противоречивое понятие. Наивысшим математическом выражением той эпохи стала Евклидова геометрия и аксиома Евдокса-Архимеда, задающая потенциальную бесконечность.

Однако из этого не следует, что в будущем будет наблюдаться возврат к представлению о том, что Евклидова геометрия эквивалентна истине. Местонахождение точки G по сравнению с точкой C оказывается ближе к началу системы координат, которое условно можно назвать «абсолютной истиной». Иначе говоря, это смещение можно интерпретировать как обнаружение некоего изъяна в Евклидовой геометрии, на который в течение многих веков математики не обращали внимания, будучи убежденными в ее полной непротиворечивости. Так как Евклидовы «Элементы геометрии» были задуманы как геометрическое изложение теории гармонии (через построение пяти Платоновых тел), то в новой математической парадигме мы вправе ожидать повторной постановки проблемы гармонии, но опять-таки на основе ринципиально новых научных данных.

Наиболее близка к таким взглядам на будущее математики концепция ... А.П.Стахова, который отстаивает бесспорную для всех историков математики (и крайне неприятную для современных жрецов науки) вещь, а именно то, что наука математика зарождалась в неразрывной взаимосвязи трех основных проблем: проблемы измерения (геометрия, тригонометрия), проблемы счета (арифметика, системы счисления), а также проблемы гармонии (систематизация и обобщение знаний). Хотя свидетельство Прокла Диадоха (V век н.э.), в котором раскрывается смысл Евклидовых «Элементов», составленных как строго аксиоматическое построение пяти правильных многогранников, имеет множество подтверждений в античной науке, современные математики продолжают от нас скрывать этот исторический факт».

Любопытна также следующая информация, содержащаяся в статье Дениса Клещева:

«Как видно из контекста главной цели Евклидова трактата само название его содержало глубокий смысл, так что «Элементы геометрии» в узком кругу афинских акадэмиков понимались как «Платоновы первоэлементы и геометрия мировых тел, состоящих из них», а не так, как принято воспринимать это название в наши дни, то есть в буквальном смысле просто «Начала геометрии». То есть, гипотеза Прокла возникла не на пустом месте. Она отражала взгляды «афинских акадэмиков» на «Начала» Евклида.

Ну и наконец, Денис Клещев приводит мнение по этому поводу Мордухай-Болтовского (самого авторитетного советского исследователя и переводчика трактата Евклида на русский язык):

«Тщательный анализ "Начал" меня решительно убеждает, что построение правильных тел, и еще более – доказательство существования пяти и только пяти тел – представляло некогда, еще до Евклида, конечную цель того труда, из которого произошли "Начала"».

А если вспомнить, что такого же взгляда на «Начала» Евклида придерживались Иоганн Кеплер и Феликс Клейн, то признание «гипотезы Прокла» современными жрецами математической науки исторически неизбежно, что приведет к революционным преобразованиям в математике и математическом образовании.

2. О тщетности некоторых «специалистов» принизить значение «математики гармонии»

В своей статье Денис Клещев говорит о беспрецедентной компании по обливанию грязью «математики гармонии» [2] и Международного Конгресса по Математике Гармонии (Одесса, 2010), которую развернула группа «современных золотоискателей». В своих попытках принизить значение «математики гармонии» эти «специалисты» не брезгуют никакими средствами (вранье, обвинение в плагиате и лженауке).

Огульное утверждение о том, что «математика гармонии» не содержит никаких новых математических результатов, легко опровергается Клещевым:

«Страстное желание опорочить математику гармонии (а, как следует из систем счисления с иррациональными основаниями Бергмана-Стахова, гармония, действительно, обладает такой специфической математикой) уже привело к появлению ряда лиц, не имеющих никакого понятия о научной этике, которые попытались пересмотреть приоритет открытия гиперболических функций Фибоначчи и Люка – Ткаченко-Стахов, 1988 год; Розин, Боднар – и присовокупить результаты этой исследовательской группы себе. Есть в мире и деструктивные силы, распространяющие мнение о «лженаучности» всей программы гармонизации математики (которой в международном научном сообществе придерживаются самые разные исследователи, а не только группа Стахова). Такие поверхностные заявления о математических работах А.П.Стахова и его коллег могут произвести впечатление лишь на студентов, не имеющих собственного мнения о математике, изучающих ее по принципу трех "З" («зазубрил, ¢здал, забыл») или по принципу Ландау («учите математику, понимание придет потом»)».

В отличие от некоторых «докторов и кандидатов каких-то наук», Денис Клещев, не отягощенный учеными степенями и званиями, вслед за академиком Митропольским [3] совершенно правильно отмечает, что «систем счисления с иррациональными основаниями» до работ Джорджа Бергмана [4] и Алексея Стахова [5,6] в математике не существовало и это открытие могло быть сделано только в рамках «гармоничной математики», основанной на золотом сечении. Но именно эти системы счисления могут быть основой не только для создания новой теории чисел [7], но и для революционных преобразований в микропроцессорной технике [8]. То же самое можно сказать и о других результатах, которые возникли в рамках «математики гармонии» [2], в частности, о гиперболических функциях Фибоначчи и Люка, «золотой» фибоначчиевой гониометрии, «золотых» матрицах, которые возникли в рамках «математики гармонии. А решение 4-й проблемы Гильберта, сделанное Алексеем Стаховым и Самуилом Арансоном и которое с пеной у рта опровергал «доктор каких-то наук»», уже признано западным математическим сообществом [9-11].

3. Об аксиомах Евдокса-Архимеда и Кантора

В своей статье Денис Клещев упоминает об одном математическом результате, полученном мною на заре научной деятельности – обнаружению противоречий в аксиомах непрерывности (аксиома Евдокса-Кантора и аксиома Дедекинда). О чем идет речь?

Моей первой математической теорией, которая была создана совместно с украинским математиком Игорем Витенько [12], является так называемая алгоритмическая теория измерения, изложенная в книге [13]. В первой главе «Проблема измерения» этой книги я провел анализ всех научных теорий, имеющих отношение к «учению об измерении», в том числе и аксиом математической теории измерения.

Этот анализ привел меня к следующим необычным выводам. Теория измерения геометрических величин, восходящая к «несоизмеримым отрезкам», основывается на группе аксиом, называемых аксиомами непрерывности [14], которые включают в себя аксиомы Евдокса-Архимеда и Кантора или аксиому Дедекинда.

Аксиома Евлокса-Архимеда («аксиома измерения»):

Для любых двух отрезков A и B (Рис. 1) можно найти такое натуральное число n, чтобы

nB > A. (1)

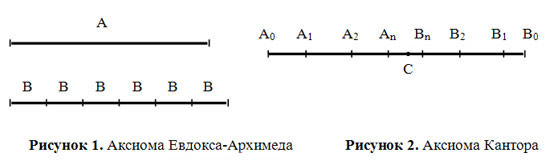
Аксиома Кантора (о «стягивающихся отрезках»):

Если задана бесконечная последовательность отрезков A₀B₀, A₁B₁, A₂B₂, ... , A_nB_n, ... (Рис. 2), «вложенных» друг в друга, то есть каждый отрезок являются частью предыдущего, тогда существует по крайней мере одна точка C, общая для всех отрезков.

Главным результатом теории геометрических величин является доказательство существования и единственности решения q «основного уравнения измерения»:

Q = qV, (2)

где V есть единица измерения; Q – измеряемая величина и q – результат измерения.

Несмотря на кажущуюся простоту сформулированных выше аксиом и всей математической теории измерения, она, тем не менее, является продуктом более чем двухтысячелетнего периода в развитии математики и содержит в себе ряд глубоких математических идей. Прежде всего, необходимо подчеркнуть, что аксиома измерения основана на "методе исчерпывания", предложенном древнегреческим геометром Евдоксом для преодоления кризиса в основаниях математики, вызванного открытием «несоизмеримых отрезков». «Метод исчерпывания» и вытекающая из него аксиома измерения имеют практическое (эмпирическое) происхождение; они были позаимствованы древнегреческими математиками в практике измерений. Аксиома измерения концентрирует тысячелетний опыт человека, задолго до возникновения аксиоматического метода в математике миллиарды раз измерявшего расстояния, площади и временные интервалы, и представляет собой сжатую формулировку алгоритма измерения отрезка А с помощью отрезка В. Суть этого алгоритма состоит в последовательном откладывании отрезка В на отрезке А и подсчете числа отрезков В, укладывающихся на отрезке А. В современной практике измерений такой метод измерения называется алгоритмом счета.

Аксиома Кантора содержит в себе еще одно удивительное достижение математической мысли - абстракцию актуальной бесконечности. Именно такое представление о бесконечном лежит в основе канторовской теории бесконечных множеств. Обнаруженные в начале 20-го века парадоксы, противоречия в канторовской теории бесконечных множеств значительно пошатнули устои математики. Были предприняты различные попытки укрепить их. Наиболее радикальной из них является конструктивное направление в обосновании математики [15], которое полностью исключает канторовскую абстракцию актуальной бесконечности и использует гораздо более «скромную» абстракцию бесконечного, называемую абстракцией потенциальной осуществимости.

Если теперь вновь обратиться к аксиомам Евдокса-Архимеда (Рис.1) и аксиоме Кантора (Рис. 2), то нетрудно обнаружить противоречие между ними. Аксиома Евдокса-Архимеда основана на использовании абстакции потенцитальной бесконечности, согласно которой число шагов n в этой аксиоме всегда конечно, но потенциально неограниченно, при этом после каждого шага допускается возможность совершения следующего шага. В аксиоме Кантора используется понятие актуальной бесконечности; при этом предполагается, что все «стягивающиеся отрезки» вместе с объединяющей их точкой С считаются заданными одновременно. Таким образом, на начальном этапе доказательства уравнения (1) мы используем понятие потенциальной бесконечности (аксиома Евдокса-Архимеда), а на завершающем этапе мы «перепрыгиваем» через это понятие и используем понятие актуальной бесконечности (аксиома Кантора).

В этой связи уместно я хотел бы привести цитату из моей книги [13]:

«Уместно обратить внимание на внутреннюю противоречивость ... теоретико-множественной теории измерения (и как следствие теории действительных чисел), допускающей в своих исходных положениях (аксиомы непрерывности) сосуществование диалектически противоречивых представлений о бесконечном (актуальной, "статической", завершенной бесконечности – в аксиомах Кантора, (и Дедекинда) и бесконечности потенциальной, "становящейся", незавершенной – в аксиоме Архимеда)».

То есть, существующая теория измерения и вытекающая из нее теория действительных чисел, основанные на аксиоме Кантора, являются внутренне противоречивыми и такие теории не могут быть положены в основание математики! Иначе и вся математика становится внутренне противоречивой теорией. Что на самом деле и случилось в математике в начале 20-го века, когда были обнаружены противоречия в канторовской теории бесконечных множеств. Удивительно, что такая простая идея до сих пор не была замечена математиками.

В последние годы в работах российского математика Александра Зенкина [16], а также в работах других авторов [17,18] были предприняты радикальные попытки «очищения» математики от канторовской теории бесконечных множеств. Анализ канторовской теории бесконечных множеств, изложенный в статье [16], привел Александра Зенкина к заключению, что доказательства многих теорем Кантора о бесконечных множествах являются логически некорректными, а вся «теория Кантора» в некотором смысле является «мистификацией». Математики 19-го века были очарованы Кантором и приняли его удивительную теорию без должного критического анализа и даже возвели эту теорию в ранг величайших математических открытий 19-го века, лежащих в основаниях математики. Обнаружение парадоксов в канторовской теории бесконечных множеств значительно остудило восторг математиков этой теорией, но окончательную точку в критическом анализе теории Кантора поставил Александр Зенкин [16]. Он показал, что главной ошибкой Кантора было принятие абстракции актуальной бесконечности, что недопустимо в математике. Но без абстракции актуальной бесконечности теория бесконечных множеств Кантора является несостоятельной! Впервые на эту проблему обратил внимание Аристотель, который первым предупредил о невозможности использования понятия «актуальной бесконечности» в математике.

Таким образом, «Канторовская теория бесконечных множеств» является ни чем иным, как величайшей математической мистификацией 19-го века, и ее принятие математиками 19-го века без должного критического анализа является одной из «стратегических ошибок» в развитии математики [17], следствием чего и стало возникновение современного кризиса в основаниях математики.

Детальный критический анализ проблемы бесконечного в математике дан в статье Алексея Стахова и Дениса Клещева [18]. Статья посвящена светлой памяти Александра Зенкина.

Таким образом, уже в 70-е годы 20-го века логика создания алгоритмической теории измерения привела меня к обнаружению противоречий в аксиомах непрерывности (Евдокса-Архимеда и Кантора). В тот период я еще не сознавал до конца, что прикоснулся к одной из фундаментальных проблем, лежащих в основании математики.

4. Заключение

В чем состоит основное значение статьи Дениса Клещева? Видимо, в следующем. Как отмечает академик А.Н. Колмогоров в книге «Математика в ее историческом развитии» (1991), создание «математики как особой науки, имеющей собственный предмет и метод» произошло в Древней Греции. При этом древнегреческая математика создавалась под мощным влиянием античных представлений о гармонии мироздания, которая ассоциировалась у древних греков с Платоновыми телами и «золотым сечением». Эта проблема получила наилучшее отражение в «Началах» Евклида, которые, по мнению «афинских акадэмиков», понимались как «Платоновы первоэлементы и геометрия мировых тел, состоящих из них». Процесс создания математики в Древней Греции под влиянием античных представлений о гармонии можно назвать МАТЕМАТИЗАЦИЕЙ ГАРМОНИИ, а сама математика, созданная древними греками, есть ни что иное, как МАТЕМАТИКА ГАРМОНИИ. Эта идея отражена в небольшой статье «Гармония сфер», помещенной в The Oxford dictionary of philosophy‎ [20]. Проанализируем эту статью:

«Harmony of spheres. A doctrine often traced to Pythagoras and fusing together mathematics, music, and astronomy. In essence the heavenly bodies being large objects in motion, must produce music. The perfection of the celestial world requires that this music be harmonious, it is hidden from our ears only because it is always present.         The mathematics of harmony was a central discovery of immense significance to the Pythagoreans».

«Гармония сфер. В этой доктрине, часто приписываемой Пифагору, происходит объединение математики, музыки и астрономии. Ее сущность состоит в том, что небесные тела, будучи огромными объектами, при своем движении должны производить музыку. Совершенство небесного мира требует, чтобы эта музыка была гармоничной, она скрыта от наших ушей только потому, что всегда присутствует. Математики гармонии была центральным открытием огромного значения для пифагорейцев».

Еще одно упоминание о «математике гармонии» мы встречаем в книге Vladimir Dimitrov. A new kind of social science. Study of self-organization of human dynamics, опубликованной в 2005 г. [21]. Приведем цитату из этой книги:

«Harmony was a key concept of the Greeks, a conjunction of three strands of meaning. Its root meaning was aro, join, so harmonia was what joined. Another meaning was proportion, the balance of things that allowed an easy fit. The quality of joining and proportion then came to be seen in music and other arts.

The precondition for harmony for the Greeks was expressed in the phrase “nothing to much”. It also had a mysterious positive quality, which became the object of enquiry of their finest minds. Thinkers such as Pythagoras sought to capture the mystery of harmony as something both inexpressible yet also illuminated by mathematics. The mathematics of harmony explored by the ancient Greeks is still an inspiring model for contemporary scientists. Crucial to it is their discovery of its quantitative expression in astonishing diversity and complexity of nature through the golden mean (golden ratio), Ф (phi): 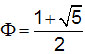, which is approximately equal to 1.618. It is described by Euclid in book five of his Elements: “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to greater, so is greater to the less”.

«Гармония была ключевой концепцией греков, с помощью которой осуществлялась связь трех значений. Его корневое значение было aro, соединение, гармония было то, что соединяет. Другое значение было пропорция, баланс вещей, который позволял простое соединение. Качество соединения и пропорции позже стали рассматриваться в музыке и других видах искусства.

Предпосылка для гармонии для греков была выражена во фразе "ничего лишнего"​​. Эта фраза содержала таинственные положительные качества, которые стали объектом исследования лучших умов. Мыслители, такие как Пифагор, стремились раскрыть тайну гармонии как нечто невыразимое и освещенное математикой. Математики гармонии, изученная древними греками, по-прежнему является вдохновляющей моделью для современных ученых. Решающее значение для этого имело открытие количественного выражение гармонии, во всем удивительном разнообразии и сложности природы, через золотое сечение Ф (фи):, что приблизительно равно 1,618. Золотое сечение описано Евклидом в Книге V его «Начал»: "Говорят, что прямая линия, может быть разделена в крайнем и среднем отношении, когда, вся линия так относится к большей части, как большая часть к меньшей".

Заметим, что в книге [21] понятие “the mathematics of harmony” непосредственно ассоциируется с «золотым сечением» - важнейшим математическим открытием античной науки в области гармонии, которое в тот период называлось «делением отрезка в крайнем и среднем отношении».

Что же происходит с современной математикой? Есть все основания предполагать, что новая парадигма математики будет связана с процессом ГАРМОНИЗАЦИИ МАТЕМАТИКИ, что приведет к революционным преобразованиям всего теоретического естествознания и математического образования. Первым шагом в этом направлении является введение курса «Математика гармонии» в учебные программы школ, колледжей и университетов. Процессы гармонизации уже проникли в теоретическое естествознание, которое широко использует Платоновы тела и «золотое сечение» в своих моделях и структурах. То есть, теоретическое естествознание в этом отношении уже опередило математику и требует от математики более активных шагов в направлении гармонизации, как самой математики, так и математического образования.

Литература

1. Д. Клещев, О былых и грядущих богах, жрецах и пророках науки // «Академия Тринитаризма», М., Эл № 77-6567, публ.16762, 17.08.2011

2. Stakhov A.P. The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science. World Scientific, 2009

3. Митропольский Ю.А. Отзыв о научном направлении украинского ученого, доктора технических наук, профессора Алексея Петровича Стахова // «Академия Тринитаризма», М., Эл № 77-6567, публ.12452, 23.09.2005

4. Bergman G. A number system with an irrational base // Mathematics Magazine, 1957, No 31: 98-119.

5. Стахов А.П. «Золотая» пропорция в цифровой технике. Автоматика и вычислительная техника, №1, 1980 г.

6. Стахов А.П. Коды золотой пропорции. Москва, Радио и связь, 1984 г.

7. Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. Украинский математический журнал, том. 56, 2004 г.

8. А.П. Стахов, Микропроцессоры Фибоначчи - как одна из базисных инноваций будущего технологического уклада, изменяющих уровень информационной безопасности систем // «Академия Тринитаризма», М., Эл № 77-6567, публ.16759, 16.08.2011

9. A. Stakhov, S. Aranson. Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem. Part I. Hyperbolic Fibonacci and Lucas Functions and “Golden” Fibonacci Goniometry. Applied Mathematics, 2011, 2 (January), 74-84

10. A. Stakhov, S. Aranson. Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem. Part II. A New Geometric Theory of Phyllotaxis (Bodnar’s Geometry). Applied Mathematics, 2011, 2 (February), 181-188

11. A. Stakhov, S. Aranson. Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem. Part III. An Original Solution of Hilbert’s Fourth Problem. Applied Mathematics, 2011, 2 (March).

12. Витенько И.В., Стахов А.П. Теория оптимальных алгоритмов аналого-цифрового преобразования. – В кн. Приборы и системы автоматики, вып. 11. Харьков, Изд-во Харьковского университета, 1970.

13. Стахов А.П. Введение в алгоритмическую теорию измерения. Москва, Советское Радио, 1977 г.

14. Бахвалов С.В., Иваницкая В.П. Основания геометрии. Москва: Издательство «Высшая школа», 1972.

15. Марков А.А. О логике конструктивной математики. Москва: Знание, 1972.

16. Зенкин А.А. Ошибка Георга Кантора // Вопросы философии. 2000, №2.

17. А.П. Стахов, Стратегические ошибки» в развитии математики // Академия Тринитаризма, М., Эл № 77-6567, публ.14555, 27.08.2007

18. Стахов А.П., Клещев Д.С., Проблема бесконечного в математике и философии от Аристотеля до А.Зенкина // «Академия Тринитаризма», М., Эл № 77-6567, публ.15680, 03.12.2009

20. Harmony of spheres. The Oxford dictionary of philosophy‎, Oxford University Press, 1994, 1996, 2005

21. Vladimir Dimitrov. A new kind of social science. Study of self-organization of human dynamics. Morrisville Lulu Press, 2005.