Настоящая статья преследует две цели. Первая – изложить новый подход к Платоновым телам (ПТ), основанный на понятиях энтропии и рекурсии. Наилучшими (близкими к характеристикам «золотого сечения») энтропийными характеристиками среди ПТ обладают додекаэдр и дуальный к нему икосаэдр. Вторая цель – осветить роль ПТ в контексте развития математики и науки в целом. Необычной является оценка роли ПТ в создании «Начал» Евклида. Согласно «гипотезе Прокла» развитие математики, начиная с Евклида, осуществлялось в двух направлениях: «Классическая математика» (позаимствовала в «Началах» аксиоматический подход, теорию чисел и теорию иррациональностей) и «Математика гармонии» (основана на ПТ и «золотом сечении»). Обсуждаются результаты использования ПТ в науке прошлых веков («Божественная пропорция» Пачоли, «Космический кубок» Кеплера, «икосаэдрическая идея» Клейна). Приводятся примеры современных научных открытий, основанных на ПТ (квазикристаллы, фуллерены, новый подход к созданию теории элементарных частиц). Роль ПТ и «золотого сечения» в развитии математики и теоретического естествознания до конца еще не раскрыта. По своему влиянию на развитие математики и науки в целом ПТ вместе с «золотым сечением» можно поставить в один ряд не только с теоремой Пифагора (Кеплер), но и с натуральными и иррациональными числами. «Вперед, к Платону!» - это достойный девиз для современной математики и естествознания.

Содержание:

1. Платоновы тела
2. Симметрия Платоновых тел
3. Связь Платоновых тел с «золотым сечением»

4. Гипотеза Прокла: с какой целью Евклид написал свои «Начала»?
5. Новый взгляд на развитие математики, вытекающий из гипотезы Прокла
6. «Космический кубок» Иоганна Кеплера
7. Платоновы тела и «золотое сечение» в «Божественной пропорции» Луки Пачоли
8. Икосаэдрическая идея Феликса Клейна
9. Квазикристаллы Дана Шехтмана
10. Фуллерены (Нобелевская Премия по химии - 1996)
11. Новые подходы в теории элементарных частиц
12. Экспериментальное доказательство проявления «золотого сечения» в квантовом мире
13. Сюрпризы для теоретического естествознания
14. Символы Шлефли и алгебраическое доказательство существования пяти Платоновых тел
15. Рекурсии Платоновых тел
16. Формула Эйлера для многогранников в дифференциальном виде
17. Энтропия Платоновых тел
18. Рабочие точки Платоновых тел на гармонической гиперболе
19. Заключение: Платоновы тела как уникальные геометрические объекты науки и природы

Литература

1. Платоновы тела

Правильные многогранники известны с древнейших времён. Но почему правильные многогранники называют Платоновыми телами?

Платон (428-348 до н.э.) в своих трудах много внимания уделил взглядам пифагорейцев на правильные тела, поскольку и сам считал, что вся Вселенная имеет форму додекаэдра, а материя состоит из атомов четырех типов, которые имеют форму тетраэдров, кубов, октаэдров и икосаэдров. Он первым воспел красоту правильных выпуклых многогранников, обладающих удивительной симметрией в трёхмерном пространстве. Грани этих многогранников – это правильные многоугольники с одинаковым числом сторон; в каждой вершине многогранников сходится одинаковое число рёбер. Примечательно, что все пять Платоновых тел в разные времена использовались в качестве игральных костей.

Теэтет Афинский (417 - 369 до н. э.), современник Платона, дал математическое описание правильных многогранников и первое известное доказательство того, что их ровно пять.

После них эстафету принял Евклид (365-300 до н.э.). В заключительной книге знаменитых «Начал» Евклид дал не только полный, подробный анализ Платоновых тел, но и простейшее геометрическое доказательство существования не более пяти правильных тел.

Теории многогранников посвящено много книг. Одной из наиболее известных является книга английского математика М. Венниджера «Модели многогранников». В русском переводе эта книга опубликована издательством «Мир» в 1974 г. Эпиграфом к книге выбрано высказывание Бертрана Рассела: «Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».

Эта мысль Бертрана Рассела, прежде всего, может быть отнесена к правильным многогранникам, с которых и начинается книга М. Венниджера. Эти многогранники принято называть Платоновыми телами, названными так в честь древнегреческого философа Платона, который использовал правильные многогранники в своей космологии. Мы начнем наше рассмотрение с правильных многогранников, гранями которых являются равносторонние треугольники.

Первый из них – это тетраэдр (Рис.1-а). В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников.

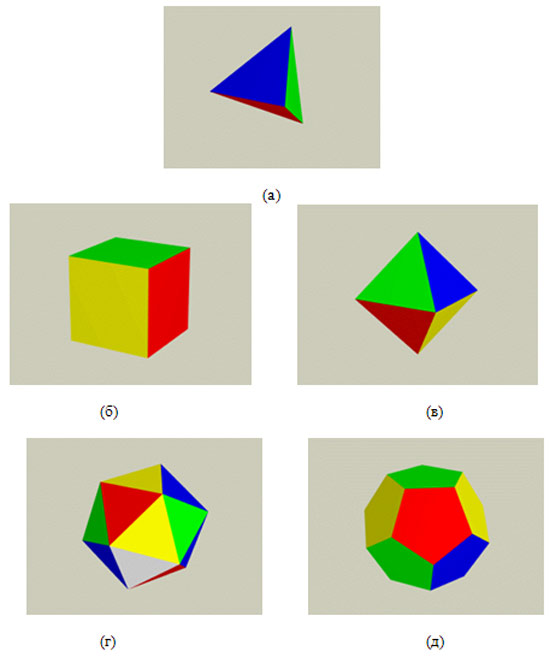
Рисунок 1. Платоновы тела: (а) тетраэдр («Огонь»), (б) гексаэдр или куб («Земля»),

(в) октаэдр («Воздух»), (г) икосаэдр («Вода»), (д) додекаэдр («Вселенский разум»)

Следующее тело, которое образуется равносторонними треугольниками, называется октаэдром (Рис.1-б). В октаэдре в одной вершине встречаются четыре треугольника; в результате получается пирамида с четырехугольным основанием. Если соединить две такие пирамиды основаниями, то получится симметричное тело с восемью треугольными гранями – октаэдр.

Теперь можно попробовать соединить в одной точке пять равносторонних треугольников. В результате получится фигура с 20 треугольными гранями – икосаэдр (Рис.1-г). Следующая правильная форма многоугольника – квадрат. Если соединить три квадрата в одной точке и затем добавить еще три, мы получим совершенную форму с шестью гранями, называемую гексаэдром или кубом (Рис. 1-в).

Наконец, существует еще одна возможность построения правильного многогранника, основанная на использовании следующего правильного многоугольника – пентагона. Если собрать 12 пентагонов таким образом, чтобы в каждой точке встречалось три пентагона, то получим еще одно Платоново тело, называемое додекаэдром (Рис.1-д).

Следующим правильным многоугольником является шестиугольник. Однако если соединить три шестиугольника в одной точке, то мы получим плоскость, то есть, из шестиугольников нельзя построить объемную фигуру. Любые другие правильные многоугольники выше шестиугольника не могут образовывать тел вообще. Из этих рассуждений вытекает, что существует только пять правильных многогранников, гранями которых могут быть только равносторонние треугольники, квадраты и пентагоны.

формате PDF (719Кб)