Статья И.В. Ерохова посвящена приложениям «золотого сечения» в схемах электрических цепей. В свое время я этим очень плотно занимался и некоторые из таких цепей (резистивные делители для цифро-аналоговых преобразователей, построенных наоснове золотой р-пропорции) описаны в некоторых из моих ранних статтей, например, в статье Стахов А.П. Цифровая метрология в кодах Фибоначчи и кодах золотой пропорции. В сборнике «Современные проблемы метрологии». Москва, Изд-во Всесоюзного заочного машиностроительного института, 1978 г. Тем не менее статья Ерохина содержит ряд интересных научных находок, которые меня заинтресовали. В частности, формулы (18), (19), позволяющие представить отношение соседних р-чисел Фибоначчи в виде цепной дроби, являются новыми. Основным недостатком статьи Ерохина (как впрочем и многих других исследователей, занимающихся приложением «золотого сечения» в теории электрических цепей и электросвязи) является отсутствие ссылок на работы «пионеров» в этой области. Я имею в виду прежде всего книгу современного исследователя, египетскогго математика и специалиста в области электрических цепей Мидхата Газале (Gazale Midhat J. Gnomon. From Pharaohs to Fractals. Princeton, New Jersey: Princeton University Press, 1999 (русский перевод, 2002).), который задолго до Ясинского и других исследователей в этой области развил «золотую» прикладную математику применительно к электрическим цепям и электросвязи.

Аннотация. В статье приводится алгоритм получения функций входного сопротивления для разных электрических цепей. При единичных параметрах цепи выражение функции можно рассматривать как ее структуру.

Предлагается представлять сложные структуры как объединение простых, которые выражают численно принадлежность к определенному типу симметрии.

Вступление

Понятие «структура » используется чаще всего применительно к электрической цепи как единому целому. Структура схемной функции интересует исследователей реже, хотя никто не станет спорить, что она определяется схемой соединения элементов электрической цепи. Создается впечатление, что внимания специалистов в области теории электрических цепей заслуживает единственная схемная функция (входное сопротивление) электрической схемы, которая носит название лестничной [1].

Получение функции входного сопротивления лестничной схемы

Рассмотрим известную электрическую цепь, рис. 1.

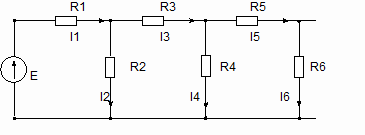
Рис. 1. Изображение лестничной схемы.

Традиционно схему принято изображать именно так, как показано на рис.1, хотя очевидно, что все четные элементы имеют общий узел, а ячейки схемы представляют собой контура с тремя сторонами. Треугольные ячейки образуют некоторое подобие пчелиных сот, а наличие общей вершины делает граф похожим на круг, где четные элементы выступают в роли радиуса. Таким образом, сходство с лестницей весьма отдаленное. Заметим, что число звеньев лестничной схемы может быть произвольным, а в пределе – бесконечным.

В работе [2] приведен интересный алгоритм получения выражения для входного сопротивления схемы рис.1:

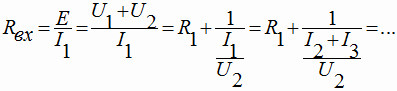
(1)

Как видно из (1), в процессе преобразований применяются оба закона Кирхгофа:

(2)

Повторение операций к другим звеньям лестничной схемы дает в пределе бесконечную простую цепную дробь [3]. Этот математический объект был известен еще древним египтянам, которые использовали его замечательные вычислительные свойства при решении различных задач. В теорию электрических цепей простая цепная дробь была введена немецким ученым-электротехником Вильгельмом Кауэром. Он исследовал лестничные электрические фильтры, т.е. цепи переменного тока [1].

Итак, продолжение преобразований (1) дает в результате выражение (3), известное как форма Кауэра:

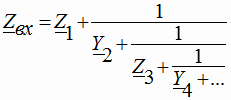(3)

Рассмотрим особый случай. Допустим, что все параметры схемы численно равны:

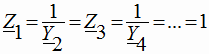
тогда выражение (3) принимает следующий вид:

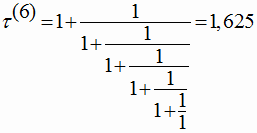(4)

Простая цепная дробь (4) является особой формой замечательного числа , известного в математике как греческое сечение.

Значение числа может быть получено формально из числового ряда Фибоначчи:

1, 1, 2, 3, 5, 8, 13, …

(5)

Каждый член ряда (5), начиная с третьего, вычисляется по формуле:

,

(6)

где I – номер элемента в ряде (5).

Предел соотношения двух членов ряда Фибоначчи существует и равен :

.

(7)

Покажем это на простом примере соотношения двух конкретных чисел ряда (5):

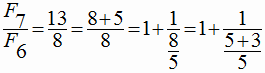(8)

Выражение (8) содержит полный цикл преобразования, которое может быть продолжено:

.

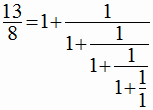(9)

Выражения (4) и (9) совпадают. Таким образом, структура схемной функции лестничной схемы (3) может быть получена формально по алгоритму (8), который очень похож на процедуру последовательного деления (1) с применением законов теории электрических цепей. Заметим, что в случае преобразования (8) равенство (6) применяется аналогично законам Кирхгофа (2) в преобразовании (1).

Распространение преобразования на другие схемы

Проведем рассмотрение особенностей применения алгоритма последовательного деления на более сложной электрической цепи – схеме моста Уинстона, рис.2.

Аналогично предыдущему примеру определим входное сопротивление схемы рис.2 между узлами 1*, 4:

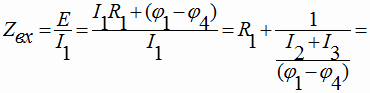
(10)

Как видно из выражения (10), в процессе преобразования были использованы второй и первый законы Кирхгофа, выполнен полный цикл. Далее, делим слагаемые второго этажа дроби (10) на разность потенциалов и представляем ее как ветвь одного из двух контуров:

.

Цикл преобразования повторяется.

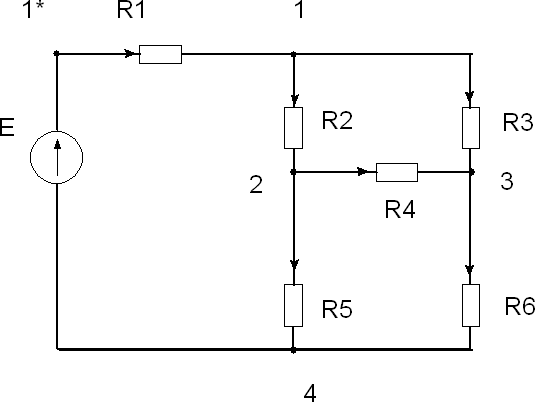
Рис. 2. Схема моста Уинстона.

В результате выполнения нескольких циклов преобразования получаем следующее выражение:

.

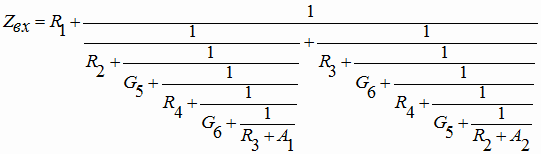(11)

Отметим, что цепная дробь (11) является более сложной, чем формула входного сопротивления лестничной схемы (3). Некоторое сходство выражений не устраняет существенного различия – преобразование (11) не закончено. В последнем этаже дроби присутствуют слагаемые, которые являются остатком деления в каждой из двух ветвей цепной дроби (11).

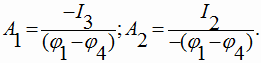
Другими словами, преобразование может быть продолжено почти с начала (10). Причем, левое слагаемое второго этажа дроби получит продолжение, аналогичное правому слагаемому, а правое слагаемое второго этажа будет продолжено аналогично левому. Таким образом, в выражении (11) появляется периодичность, т.е. обнаруживаются признаки фрактальности.

Для случая особого распределения численных значений параметров схемы рис.2 получим выражение, аналогичное (4).

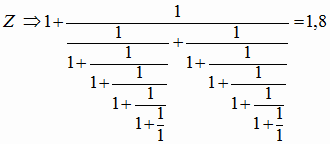(12)

При получении дроби (12) остатки были приравнены нулю, таким образом, данное выражение является приближенным.

Геометрический аспект преобразования

Простой цепной дроби (3) ставится в соответствие следующий геометрический объект [4]:

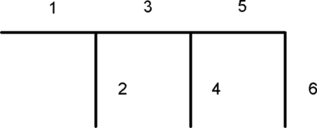
Рис.3. Граф, соответствующий дроби (3).

В этой работе граф рис.3 ошибочно определяется как дерево электрической цепи рис.1. Ошибка очевидна, так как граф рис.3 содержит все ветви электрической цепи рис.1 (в дереве отсутствуют ветви-связи). Сходство с деревом лишь в том, что топологический объект рис.3 не содержит ни одного контура. Подобный граф можно получить из лестничной схемы, рис.1, только одним способом – «расщеплением» общего узла.

Анализируя выражение (11), можно заметить, что оно является определенным объединение двух лестничных схем, рис.4. Каждая из двух ветвей дроби (11) изображена отдельно. Остаток, образовавшийся при последовательном делении, не принимается во внимание.

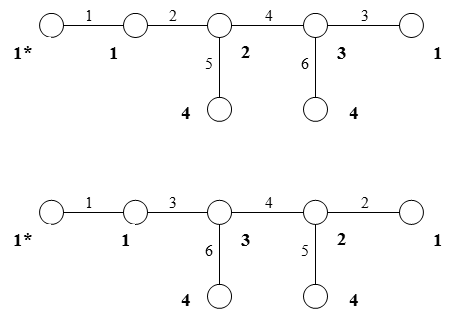
Рис.4. Графы, аналогичные рис.3.

Графы рис.4 (рис.3) содержат все ветви электрической цепи рис.2 (рис.1). Оба геометрических объекта не содержат контуров, так как расщеплены соответствующие узлы (на рис.4 – узлы 1 и 4). Объединим графы, представленные на рис.4, чтобы наглядно представить геометрический объект, соответствующий цепной дроби (11).

Рис.5. Геометрический объект, соответствующий дроби (11).

Итак, на рис.5 представлена структура схемной функции (11), сама дробь отличается от простой цепной дроби (3) не только рисунком, но и названием – ветвящаяся цепная дробь [4].

Новый математический объект обладает уникальными свойствами, которые делают возможным производить приближенные вычисления значений схемных функций. Кроме того, представление схемных функций в виде ветвящейся цепной дроби позволяет представлять сложную структуру как объединение более простых, рис.4. Ветвящуюся цепную дробь можно получить как с помощью математических алгоритмов [4], так и с помощью представленных выше преобразований графа-схемы.

Формальное получение опорных структур

Существует большое количество числовых последовательностей, которые дают возможность вычислять значения, аналогичные . Иррациональное число, которое получается из (7), является частным случаем индекса определенной симметрии и носит название золотого (греческого) сечения. Более сложные типы симметрии выражаются с помощью обобщенных чисел Фибоначчи (р – чисел Фибоначчи) [5]:

Для заданного p = 0, 1, 2, 3,... числовые последовательности Fp(n) получают с помощью следующих рекуррентных соотношений:

Эти числовые последовательности включают в себя как ряд значений (p = 0), так и классический ряд Фибоначчи (p = 1).

На каждой численной последовательности (13) можно определить соотношение, аналогичное (7):

.

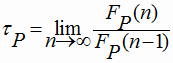(14)

По формуле (14) вычисляются значения обобщенных золотых сечений.

Численные значения обобщенного золотого сечения характеризуют разные виды симметрии. Приведем для сравнения только некоторые из них (при р=0,1,2,3,4):

(15)

Очевидно, что тип симметрии, представляемой второй строчкой (15), соответствует лестничной схеме. Без сомнения, последующие строчки (15) представляют другие математические структуры.

В качестве примера исследуем числовую последовательность, соответствующую третьей строчке записи (15):

1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60,…

(16)

Запишем итерационную формулу, по которой вычисляются члены числовой последовательности (16):

.

(17)

Раскроем соотношение двух конкретных членов ряда (16):

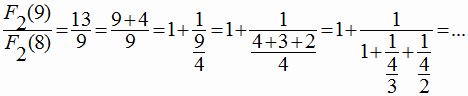(18)

Если преобразование (18) довести до логического конца, то получится следующая ветвящаяся цепная дробь:

.

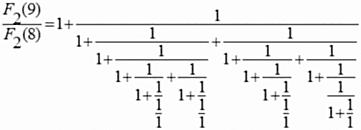(19)

Численное значение дроби (19) равно 1.4444…, что является определенным приближением индекса симметрии, представленной третьей строчкой (15).

Как было показано выше, выражение (19) является структурой некоторой функции схемы, граф которой отличается от графа лестничной схемы.

Легко убедиться, что выражения, подобные (19), можно получить по алгоритму (18) для других значений . Вероятно, числа Фибоначчи могут послужить основой для получения опорных структур, на которых в дальнейшем может быть построена классификация графов электрических цепей.

Заключение

В статье на классическом примере показано, что известный алгоритм получения формы Кауэра можно распространить на электрические цепи, отличающиеся от лестничной схемы. В результате применения преобразования (1), (10) получается цепная дробь, элементами которой являются параметры элементов электрической цепи. При «особых» численных значениях параметров дробь превращается в математический объект, который имеет геометрическую интерпретацию. Новому топологическому образованию присвоено название структуры схемной функции.

Структура схемной функции содержит все ветви графа электрической цепи, которые не образуют ни одного контура. Однако, если при образовании дерева электрической цепи контура разрываются с помощью удаления ветвей-связей, то в случае структуры схемной функции контура разрываются с помощью дуальной процедуры – расщеплением некоторых узлов, рис.3, рис.5.

Было показано, что при условии бесконечного последовательного деления (преобразование включает бесконечное число циклов), структура схемной функции обнаруживает свойства фрактала [6].

Литература

1. Cauer W. Theorie der linearen Wechselstromschaltungen. – Berlin: Akademie Verlag, 1954. — 586s.
2. Херреро Д., Уиллонер Г. Синтез фильтров, — М.: Сов. Радио, 1971. – 232с.
3. Хинчин А.Я. Цепные дроби. – М.: Наука, 1978. – 112с.
4. Скоробогатько В.Я. Теория ветвящихся цепных дробей и ее применение в вычислительной математике. – М.: Наука. Глав. ред. Физ.-мат. лит., 1983. – 312с.
5. Обобщенные числа Фибоначчи. – http://www.goldenmuseum.com/
6. Бецкий О.В., Лебедева Н.Н. Фракталы в биологии и медицине. // Биомедицинские технологии и радиоэлектроника, №10-11, 2002. – с.49-59.