|
|
|
Н.А. Шило, А.В. Динков
Комментарий А.П. Стахова
Суть работы Н.А. Шило и А.В. Динкова состоит в следующем. Основываясь на гипотезе Д.И. Менделеева о том, что «...система требует телесной формы, допускающей сближение по всем направлениям» и что периодический закон «...следует выражать не геометрическими линиями, всегда подразумевающими сплошность, а вроде того, как поступают в теории чисел — прерывно», авторы выдвигают смелую гипотезу о том, что «место каждого химического элемента в системе определяется не арифметической прогрессией..., а распределением Фибоначчи».
Авторы обращают внимание на аналогию между экспоненциальной функцией N = N() e –λ t, которая моделирует процесс радиопктивного распада, и рядом Фибоначчи. Суть этой аналогии состоит в том, что «любая производная этого процесса по времени дает с точностью до множителя сам процесс, т.е. повторяет функциональную зависимость». Именно таким свойством обладает ряд Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,.... для которого первые и последующие разности (или производные) повторяют сам ряд.
Авторы обращают внимание на тот факт, что «идею спиральной формы таблицы химических элементов высказал Д.И.Менделеев уже в первой статье о периодическом законе. Это было его гениальное предвидение. Позднее в итоговой статье «Периодическая законность химических элементов» он писал: «В сущности же все распределение элементов представляет непрерывность и отвечает до некоторой степени спиральной функции»... Теперь очевидно, что все интуитивные и пророческие идеи Д.И.Менделеева можно совместить в пространственной спиральной форме периодического закона».
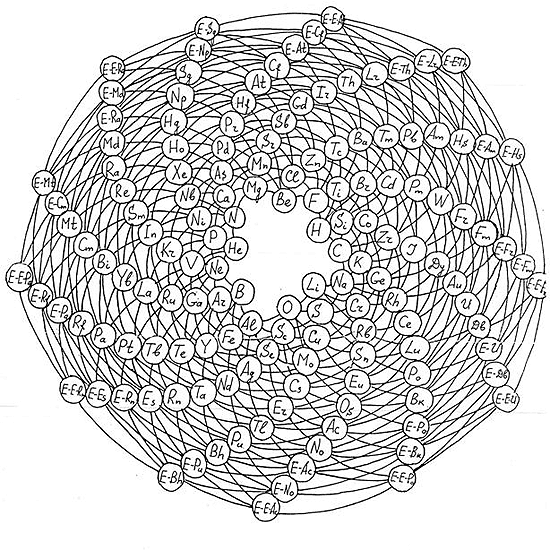
Итак, согласно мнению авторов, «пространственная кривая (спираль), на которой находятся элементы, расположена внутри конуса или в псевдосфере Н.И.Лобаческого. Элементы на этой спирали представлены дискретными точками (или «шариками»). Проекции элементов на горизонтальную плоскость, т.е. плоскость основания конуса, дают фибоначчиевые спирали, т.е. такие спирали, на любой из которых разности между атомными номерами любых двух последовательных элементов дают числа ряда Фибоначчи».
Эта идея авторов по существу сводится к утверждению о гиперболическом характере процессов, лежащих в основе образования Периодической системы элементов. А возникновение при этом чисел Фибоначчи в Периодической системе свидетельствует о «фибоначчиевой» гиперболичности Периодической системы. То есть, Периодическая система химических элементов основана на «гиперболичских функциях Фибоначчи и Люка», развитых мною в последние годы совместно с украинскими учеными И.С. Ткаченко и Б.Н. Розиным (см. например, мою статью «Гиперболические функции Фибоначчи и Люка:история и приложения», опубликованную на сайте «Академия Тринитаризма» http://www.trinitas.ru/rus/doc/0232/009a/02321057.htm.
Я думаю, что именно гиперболические функции Фибоначчи и Люка и являются тем математическим инструментом, которые приведет авторов к завершенной теории Периодической системы.
Подводя итог, я предложил бы назвать рассматриваемую статью «Фибоначчиевая интерпретация Периодической системы элементов Д.И. Менделеева». Однако, независимо от названия ясно одно: в статье речь идет о новом фундаментальном научном открытии, которое затрагивает все области современного теоретического естествознания. И нельзя не согласиться с мнением авторов о том, что «идя по этому пути, мы неизбежно придем к совершенно новому пониманию многих процессов и явлений, может быть, даже изменим свои представления о мироздании».
Начнем с того тривиального факта, что в настоящее время в основе современной химии лежит широко распространенная периодическая система элементов Д.И.Менделеева, в которой 14 элементов от Се до Lu, а также 14 элементов от Th до Lr вынесены за пределы системы. Таким образом, на практике фактически используется не одна таблица, а две. Однако, сам Д.И.Менделеев, называя свою систему периодической по группам и рядам, не допускал даже мысли о возможности исключения из нее хотя бы одного элемента.
Вопросы современного развития и усовершенствования периодической системы довольно подробно рассмотрены в монографии [1], в которой на основе анализа электронного строения и степеней окисления элементов получена одна из форм периодической системы с размещением по группам всех лантанидов, актинидов и металлов триад, как наиболее точно отражающая строение и свойства элементов.
В 1999 г. предложена дублетно-концентрическая форма периодической системы элементов [2], в которой сформулированы основные, довольно очевидные структурные правила: а)все элементы с четным зарядовым номером находятся в группах с четным зарядовым номером б)в группах с нечетным номером находятся элементы с нечетным зарядовым номером.
В том же 1999 г. опубликована так называемая Горно-Алтайская таблица химических мультиплетов KuFeRum [3]. Как полагают авторы «Таблица KuFeRum позволяет взглянуть на множество всех химических элементов как на единое целое и увидеть его внутренние законы, которым подчиняется все множество элементов, и которые не могут быть получены из квантовомеханической модели отдельного атома». В работе авторов Горно-Алтайскай таблицы [3] отмечается, что использование квантовой механики для классификации химических элементов не дает удовлетворительных результатов, тогда как Таблица KuFeRum химических мультиплетов абсолютно точно соответствует группе симметрии Румера — Фета SU(2) x SU(2) x SO(4,2), хотя не согласуются с группой симметрии Малкина — Манько SU(2) x SO(4,2). Это указывает на то, что и модель Н.Бора не может дать удовлетворительных результатов в интерпретации многих особенностей существующей периодической системы Д.И.Менделеева, что заведомо также исключает привлечение квантовой механики для объяснения внутренней структуры системы. Авторы таблицы KuFeRum, как не трудно понять, сводят изучение свойств элементов к их «внутренней симметрии» по аналогии с элементарными частицами [4].
В связи с этим обратим внимание на то, что «внутренняя симметрия» атомов, несомненно, каким-то образом связана с атомными ядрами. Это, опираясь на принцип П.Кюри, который позволяет в ходе исследований «... найти и оценить симметрию системы по известной симметрии ее подсистем и перенести соотношения симметрии с одного уровня структурной организации системы на другой» [5], нами будет показано дальше.
Авторы таблицы KuFeRum полностью исключили из своих построений атомные ядра. Ими также не рассматривается версификация наших знаний об элементах, что согласуется с ложными выводами в [4] о том, что «нельзя выделить пары элементов, атомные веса которых были бы значительно ближе, чем атомные веса в разных парах». Они, как известно, противоречат большинству физических свойств элементов, так как совершенно очевидна некоторая эквидистантность их поведения. Она проявляется в зависимостях свойств от зарядовых чисел или от атомных весов выделенных пар элементов.
В конце 19 века Г.А.Лоренц развивал мысль о том, что в соответствии с таблицей элементов соседние элементы рождались как близнецы, попарно, причем одной и той же парой оказывались элементы, мало отличающиеся друг от друга по химическому весу. Он отнес к числу близнецов все пары элементов с разностями весов, не превышающих по абсолютному значению 1,4. В настоящее время изотопия сняла вопрос о возможной связи парности элементов с атомным весом. В основе же их разделения кладутся другие параметры: четные или нечетные ряды, зарядовый номер и т.д.
Д.И.Менделеев предложил периодическую систему химических элементов 137 лет тому назад. За это время она сыграла громадную роль не только в развитии химии, но и физики, биологии, геохимии, минералоги, петрологии, кристаллографии, космохимии и других наук. Иными словами, она стимулировала научный прогресс во всех областях, где химические элементы являются основой естественных или искусственных процессов. Однако все это почти полутаровековое время ученые разных специальностей в той или иной форме высказывали неудовлетворение менделеевской системой, несмотря на признание за ней гениальных фундаментальных свойств.
Впрочем, сам Д.И.Менделеев вскоре после того, когда его детище вошло в обиход, высказал две идеи, которые до сих пор не реализованы ни в одной из многочисленных (около 1000) предложенных после него форм периодического закона.
1.«...система требует телесной формы, допускающей сближение по всем направлениям»
2. Периодический закон «...следует выражать не геометрическими линиями, всегда подразумевающими сплошность, а вроде того, как поступают в теории чисел — прерывно» [8]
Одна из идей, направленных на совершенствование периодической системы Д..И.Менделеева сводится к поиску путей сближения элементов по всем направлениям путем изображения атомов в системе не в виде четырехугольных клеток, у которых выделяются из соображений симметрии только 4 направления: вертикальное, горизонтальное и по двум диагоналям. Каждое направление имеет интерпретацию, соответствующую 8 группам, периодам, функциональным аналогам. Но опыт показывает, что часто связи между элементами не выражаются обозначенными направлениями, а имеют совсем другой характер (как в явлении изоморфизма). Очевидно, изображать атомы в системе следует в виде самых симметричных фигур, какими являются круг на плоскости или шар в пространстве (или в виде дискретных точек на плоскости или пространственных кривых). Тогда будет удобно рассматривать изменения свойств элементов в различных направлениях и при определенных условиях проектирования выделять те направления, объективный смысл которых, как группы и периоды таблицы являются эмпирически и теоретически обоснованными. Далее, элементы должны занимать пространственные позиции. Ибо интерпретация любых связей между ними на евклидовой поверхности не будет учитывать их естественной основы — физики объема среды.
Учитывая сложившуюся ситуацию, нами проведен анализ предложенных после Д.И.Менделеева систематик химических элементов, так же как и самой периодической таблицы Д.И.Менделеева. Он позволил вскрыть, прежде всего, тот необычный факт, что в основе всех систем лежат статические связи между элементами, и все они являются «как бы отражением остановленного какого-то неизвестного еще динамического процесса развития неорганического вещества» [6]. От времени до времени осуществлявшиеся работы по абстрактной теоретико-групповой классификации периодической системы элементов не обнаруживали такой динамической модели, замороженный срез которой, в сущности, и представляют собой используемые в настоящее время систематики химических элементов, не исключая и таблицу Д.И.Менделеева. Ее совершенство, как сказано выше об этом, самим автором было поставлено под сомнение.
Кроме того, групповая классификация химических элементов в том виде, в каком она сейчас используется, не обнаруживает также связей с динамическими моделями других уровней, точно также как «преобразования автоморфизма не исчерпывают всех отношений эквивалентности и порядка» [7]. В систематике Д.И.Менделеева место каждого элемента определяется числом протонов (Н — 1, Не — 2, Li — 3 U — 92), составляющих ядро. Если для упрощения рассматриваемой проблемы опустить нейтрон и некоторые другие элементарные частицы, входящие в структуру ядра, и так или иначе влияющие на физические и химические характеристики элементов, то можно предполагать, что каждый последующий элемент является продуктом аддитивности протона к предыдущему элементу. Этот вывод основывается на том, что заряд частиц входящих в структуру атомного ядра, аддитивен. Причем внешне этот процесс как бы нормируется арифметической прогрессией с разностью Δz =1, однако форму таблицы определяет ряд Δz = 2n2, где n = 1,2,3,4 (Δz = 2, 8, 18, 32), то есть групповые изменения свойств элементов. Этими же числами определяются длины периодов таблицы. Тем не менее, даже упрощенный анализ сопоставления ряда чисел арифметической прогрессии и изменений химических и физических свойств элементов в таблице Менделеева, не обнаруживают даже подобия корреляции. Порядок физических и химических изменений элементов в таблице Д.И.Менделеева отличается более сложным характером, не показывающим даже отдаленного сходства с рядом арифметической прогрессии.
Теоретические исследования разных вариантов распределения химических элементов в используемых схемах, в которых свойства элементов меняются протонной аддитивностью, обнаружили, что их позиция в таблицах нормируется более сложным законом распределения, чем арифметическая прогрессия и при значительной роли энергетической компоненты. С выяснением этого важного обстоятельства, возник вопрос: существуют ли в совокупности химических элементов какие-либо направления изменений зарядов, отличающиеся от групп и периодов таблицы Менделеева, которые были бы более предпочтительны, чем другие? Для ответа на этот вопрос нами был проведен специальный анализ атомных ядер, как подсистем таблицы Менделеева. Совершенно неожиданно работа выявила, что место каждого химического элемента в системе определяется не арифметической прогрессией, где d — протон, а распределением Фибоначчи. Иными словами, как математической модели числа разновидностей существующих в Природе атомных ядер с учетом их распространенности и основных характеристик, например, числа протонов и нейтронов и других. На такую закономерность указывает радиоактивный распад, выражающийся экспоненциальной зависимостью числа частиц во времени:
N = N() e – λ t (1).
Любая производная этого процесса по времени дает с точностью до множителя сам процесс, т.е. повторяет функциональную зависимость (1). Очевидно, в последовательных числах, отражающих свойство производных функции e – λ t, такие имеются — это любые аддитивные последовательности. Несомненно, как мы решили, какими — то из них нормируется распределение химических элементов в системе Д.И. Менделеева. Исследования показали, действительно в основе сложного распределения в его системе находится ряд Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,.... для которого первые и последующие разности (или производные) повторяют сам ряд.
Предположим теперь, что фибоначчиевые направления изменения зарядов элементов, носят фундаментальный характер и для атомов, распространяя по принципу Кюри симметрию подсистем (т.е. атомных ядер) на систему атомов — элементов. Такое предположение хорошо согласуется с автоэволюционистскими представлениями А. Лима-де-Фария: «Никакая упорядоченность, никакая форма или функция не возникает в природе и не исчезает; они только трансформируются путем комбинирования» [9].
Для атомных ядер и элементов инвариантными должны быть геометрические спиральные формы развития, комбинирующиеся по одним и тем же геометрическим формам, различные как для атомов, так и для атомных ядер.
Идею спиральной формы таблицы химических элементов высказал Д.И.Менделеев уже в первой статье о периодическом законе [6]. Это было его гениальное предвидение. Позднее в итоговой статье «Периодическая законность химических элементов» он писал: «В сущности же все распределение элементов представляет непрерывность и отвечает до некоторой степени спиральной функции». В [6] доказано, что Менделеев однажды в первые дни открытия применил двухлинейную (двухрядную) форму периодического закона. Теперь очевидно, что все интуитивные и пророческие идеи Д.И.Менделеева можно совместить в пространственной спиральной форме периодического закона.
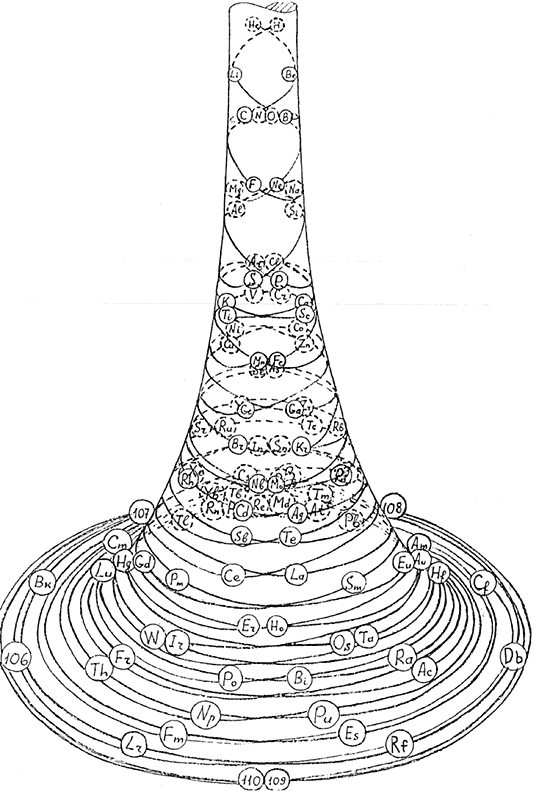
Итак, пространственная кривая (спираль), на которой находятся элементы, расположена внутри конуса или в псевдосфере Н.И.Лобаческого. Элементы на этой спирали представлены дискретными точками (или «шариками»). Проекции элементов на горизонтальную плоскость, т.е. плоскость основания конуса, дают фибоначчиевые спирали, т.е. такие спирали, на любой из которых разности между атомными номерами любых двух последовательных элементов дают числа ряда Фибоначчи. Ясно, что в силу имеющегося конечного числа элементов в Природе такие разности ограничены числом F12 = 144. На рисунке 1 представлены только спирали с Δz = 5, 8, 13, 21, 34. Спирали же с Δz = 1, 2, 3, 55, 89, чтобы не загромождать рисунок линиями, не представлены, но имеют место.
Двойные проекции элементов — сначала на плоскости, перпендикулярные основанию конуса, проходящие через его центральную ось (число таких плоскостей равно 9 — в.соответствии с числом рядов одной из форм таблицы Д.И.Менделеева, содержащей 118 элементов -ряды содержат 1 -2, 2-8, 3-8. 4-18, 5-18, 6-16. 7-16, 8-16, 9-16 элементов), а затем на боковую поверхность конуса, дают ряды таблицы Д.И.Менделеева.
Каждый предыдущий элемент на общей спирали находится по вертикальному направлению ниже последующего, т.е. удаляется по боковой поверхности от центральной оси псевдосферы. Группы таблицы Д.И.Менделеева на боковой поверхности конуса представлены некоторыми кривыми, подобными спиралям.
Если проектировать элементы на 14 вертикальных плоскостей, а затем на поверхность псевдосферы, то на этой поверхности получается короткая форма периодической системы, соответствующая приведенной в [1] с учетом структурных правил [2].
В результате таких построений становится возможным изучать симметрию свойств элементов и их соединений относительно двух осей х, у и начала координат. Заметим, что ферромагнитные Со, Ni, Gd, а также сильный парамагнетик Еu расположены на одной горизонтальной линии — (рис.2а)
Получает объяснение граница стабильности элементов Bi (после Bi нет стабильных элементов), как конечная парная граница четных ионизационных потенциалов (рис.2б). Из геометрических соображений следует возможность проявления ферромагнитных свойств у Сu и ТЬ, как физических «аналогов» Ni и Gd. Заметим, что у ТЬ уже известен ферромагнитный переход (точка Кюри Тс = 221 К). Температура перехода в антиферромагнитное состояние (точка Нееля) у Tb TN = 229 К.Проявление магнитных свойств у нанокристаллической Сu обнаружено в работе [10]
Одним из существенных эмпирических обоснований предлагаемых новых схем расположения элементов в трехмерном пространстве и их проекций на «плоскости» является выявление «разделенных» периодичностей изменения свойств элементов, таких как ионизационные потенциалы, атомные объемы, электроотрицательность и множество других.
Изучение симметрии свойств элементов в принципе должно сводиться «…к идее инвариантности некоторой конфигурации относительно определенной группы преобразований (группы автоморфизмов)…» [11]. Заметим, что в утвержденной ИЮПАК периодической таблице не содержится даже самая простая форма симметрии – зеркальная, которая имеет вид (рис.2а или рис.2б), причем физический смысл имеют оба представления – первое соответствует нечетным ионизационным потенциалам, второе – четным. Периодичность имеет место как для нейтральных атомов, так и для их ионов данной кратности. Теряя один электрон атомы элементов данной группы становятся подобными по своим свойствам атомам элементов предыдущей группы (напр. атомы щелочноземельных металлов — атомам щелочных металлов) и периодичность сохраняется. Она сохраняется и при потере к-электронов. На этом рисунке рассматривается симметричное разделение всех элементов на два класса, соответствующих нечетным и четным по заряду элементов. Как было отмечено выше, такие распределения элементов составляют двухлинейную (двухрядную) форму периодического закона. Из рис.2 видно двойственное расположение элементов В, N, Al, P и C, O, Si, O по группам IIIA, IVA, VA, VIA и IIIB, IVB, VB, VIB, аналогичное расположению H по всем группам периодической системы.
Общеизвестно также, что диссимметрия – расстройство симметрии – творит явление (П.Кюри). Поэтому, например, при нарушении плоскостной симметрии элементов, но при сохранении их зарядовой симметрии по нечетности-четности – получаем двойные фибоначчиевые расположения (рис. 3).
Идея разделения элементов на два подмножества используется в работах Ю.К.Дидыка. Основные параметры 120 известных и гипотетических элементов вещества систематизированы им по схеме L – S связи в зависимости от квантовых чисел и других характеристик [12]. Отметим положительность такого разделения, однако, наше разделение по заряду обосновывается, прежде всего, распространенностью элементов в различных природных объектах (Земля, Солнце и т.д.) «… относительная распространенность каждого элемента является для него такой существенной характеристикой, как, например, его атомный вес, или его энергия образования, или его масса. Таким образом, создается впечатление, что относительная распространенность каждого элемента, действительно, является его свойством, связанным или с другими его свойствами, или с еще неизвестным нам механизмом его образования», — пишет Э.Ферми в работе «Теория происхождения элементов» [13]. Однако любая теория должна строиться по эмпирическим количественным характеристикам. Элементы состоят из вполне определенных ядерных разновидностей (изотопов), число которых не является, по нашему убеждению, случайным фактором.
Возникновение чисел Фибоначчи в структуре связей и отношений между элементами непосредственно связано с разделением изотопов на природные и искусственные, т.к. процесс получения искусственных изотопов продолжается. «К 1950 г. был изучен изотопный состав всех природных элементов. В настоящее время уже нельзя ожидать открытия новых стабильных изотопов, т.к. почти все изотопы, соседние со стабильными, уже найдены и оказались радиоактивными» [14].
Природные изотопы в количестве 288 = 2 ∙ 144= 2 ∙ F12 = F3 ∙ F12
с учетом границы стабильности делятся на 4 совокупности по числу содержащихся в них протонов и нейтронов:
Iнн − 13 = F7; IIнч − 55 = F10; IIIчн − 55 = F10; IVчч − 165 = F4 ∙ F10
Те же самые изотопы в зависимости от их электронной конфигурации также делятся на 4 совокупности:
I S – 34 = F9; II p – 89 = F11; III d – 110 = 2 ∙ F = F3 ∙ F10; IV f – 55 = F10,
где Fi - числа Фибоначчи i = 1, 2 …
Из этих подмножеств комбинированием легко получить разделение изотопов по массовому признаку: число изотопов нечетной массы равно 2 · 55= F3 · F10, а четной – 2 · 89 = F3 · F11, а также структуру, рекомендованную ИЮПАК, как структуру вида 233 = F13 − элементы без РЗЭ и 55 = F10 − РЗЭ.
Интересно отметить, что элементы с нечетной массой нечетного и четного заряда дают отношение изотопов, равное F10 / F10 = 1, а число изотопов элементов с четным зарядом, равное 220, по признаку нечетность — четность массового числа разделяется в отношении 3:1. Т.е. четность массового числа четного по Z изотопа является доминантным признаком.
Необходимо указать еще характерные отношения, которые определяют связь с «золотым сечением», и, возможно, связаны с эволюцией атомных ядер:
1.отношение числа нуклидов четной массы к числу нуклидов нечетной массы: 2·89/2·55 ≈ φ;
2.отношение числа нуклидов четного заряда к числу нуклидов нечетного заряда:
220/68 ≈ 2 · φ,
где φ = (√5 + 1)/2-«золотое сечение»;
3.отношение числа нечетного заряда нечетного заряда нечетной массы к числу нуклидов заряда той же четности четной массы:
55/13=F10/ F7 ≈ φ3;
4.отношение чисел природных нуклидов двух подмножеств Ю.К.Дидыка
2·89/2·55 ≈ φ;
5.расположив по возрастанию зарядов 165 чет-четных нуклидов (в пределах данного заряда нуклиды располагаем по возрастанию массового числа), получим, что общеизвестные «магические» числа нейтронов 2, 8, 14, 20, 28, 50, 82, 126 соответствуют следующим номерам нуклидов нашего расположения: 1, 3, 8, 13, 21, 55, 110=2·55, 165=3·55.
Общая задача разделения множества всех элементов на подгруппы (или подмножества) для изучения свойств (одним из примеров является существующая периодическая система Д.И. Менделеева со всеми ее многочисленными формами) может быть сформулирована как задача получения небольших по размерам подгрупп элементов, которые при достаточно небольшом числе определяющих признаков, характеризующих эти подгруппы, дают возможность прогнозировать гораздо большее число их свойств или признаков и их изменений по подгруппам.
Рамки данной статьи не позволяют провести детальное решение этой достаточно трудоемкой задачи, однако, мы укажем главные, по нашему мнению, различные расположения элементов на плоскости (рис.1-4)
Далее приведем некоторые факты, касающиеся различных явлений действительности, указывающие на адекватность наших конструктивных моделей. «Существование математического факта можно считать установленным, если получена соответствующая ему конструкция в виде формул, таблиц и рисунков. Скрытая истина устанавливается на основе открытой истины, некоей видимой данности» [16].
I. Статистические распределения распространенностей элементов для выявления механизмов их образования, которые часто используются геохимиками, космохимиками, биохимиками и другими специалистами, следует проводить раздельно для нечетных и четных по Z элементов, что находится в соответствии с графиками Кларков акад. А.П. Виноградова. Рассмотрение изменений распространенностей элементов по спиралям ∆z = 2 · 5 показывает их относительно монотонный парный закономерный характер.
II. Парность магнитных свойств элементов.
а) Магнитная восприимчивость при комнатной температуре для нечетных и четных по Z элементов в парных моделях представляется совпадающими по качеству парами, т.е. или пара элементов – диамагнитна, или пара элементов парамагнитна (ферромагнитна). Исключениями являются следующие пары:
Li — Be, N — O, Al — Si.
Заметим, что модификация кислорода О3 – озон диамагнитна. Т.е. остаются 2 исключения, которые дают возможность предсказать парамагнетизм Be и Si, а так же диамагнитизм Li и Al.
О существовании намагниченности кремниевых пород сообщалось в газете «Труд», 16.09.89 г. в статье «Каждый день с чудесами». На месте катастрофы или аномального явления, произошедшего 29 января 1986 г. в районе поселка Дальнегорска Приморского края было найдено шесть пятен намагниченности кремниевых пород. «Для исследователей этот факт явился полнейшей неожиданностью, так как кремний — немагнитный материал и намагнитить его, по современным понятиям, так же невозможно как, скажем, палку или кирпич». В рамках наших построений существование парамагнитного кремния вполне очевидно.
б) Противоположные знаки температурных производных от атомных магнитных восприимчивостей переходных металлов при комнатной температуре для нечетного и четного Z:
Sc- — Ti+; V- — Cr+; Y- — Zr+; Nb- – Mo+; Tc- – Ru+; Lu- — Hf+
Исключение составляют пары Rh+ – Pd- и Ir+ – Pt-, что возможно объяснить за счет недостаточной очистки этих высокотемпературных элементов от примесей (или наличие mах у Pd и Pt на температурной зависимости χ (Т)).
в) Металлы, показывающие аномалии магнитных свойств при плавлении Р, Ag, Au находятся на одной спирали 4 · F6 [16].
г) Самый сильный в мире постоянный магнит составлен из элементов Nd, Fe, B: Nd2 Fe12 B. Элементы находятся на двух фибоначчиевых спиралях В — Fe: ∆z = 21; Fe — Nd ∆z = 34 [17].
д) Новое сверхчерное покрытие образуется из элементов Ni – P(P-5-7%) ∆z = 13
http://www.npl.co.uk/opticai.radiation/superblack.html
Интересно было бы проверить этот материал на магнетизм и сверхпроводимость.
III. На зависимости температур сверхпроводящих фаз аморфных элементов наблюдаются максимумы у спирального треугольника Nb – La − Bi со сторонами ∆z = 2 · 8; 2 · 13; 2 · 21 (рис.3а)
IY. Известно, что при плавлении Ga, Sb, Bi, Ge, Te наблюдается уменьшение объема. Разности зарядов этих элементов на разделенных по Z спиралей соответствуют фибоначчиевым кратностям (∆z = 4 · 5; 4 · 8; 4 · 13).
Можно предсказать уменьшение объема при плавлении у Ро (рис.4б)
Y. Н.А. Васютинский [18] доказал, что химические соединения, организованные по Фибоначчи, существуют, например окислы U и Cr. Заметим, что разность зарядовых чисел U и Cr равна ∆z = 2 · 34 (рис. 3б).
YI. В геологии выявлено, что в пегматитах обнаружены элементы весьма далекие по химическим свойствам в таблице Д.И. Менделеева, например, Ar, Ni, Cd, Se [19].
В нашей схеме (рис. 3б) Ar, Se находятся на спирали ∆z = 2 · 8, а Ar – Ni − Cd на спирали ∆z = 2 · 5.
YII.Заголовок монографии Н.М. Митряевой «Минералогия барито-цинково-свинцовых руд месторождений Атасуйского района» говорит о том, что Zn – Ba − Pb находятся на спирали ∆z = 2 · 13 нашей схемы (рис. 3б).
YIII. Парность элементов подтверждается зависимостями от Z: – I-ый ионизационный потенциал, сродство к электрону, электроотрицательность, атомный, ковалентный и ионный радиусы.
Отметим, что сродство к электрону следует рассматривать в схеме четных ионизационных потенциалов (рис. 2б).
IX. Периоды полураспада Т Ѕ аналогичных β+- и ε радиоактивных изотопов с Z, имеющих на один нейтрон меньше, чем 2 β - устойчивый изотоп. Отчетливо проявляются полупериоды с Z = 2 · 5.
На основании этой периодической закономерности можно оценить величину Т Ѕ у еще неизвестных изотопов: Md258, Lr264 и объяснить большие значения ТЅ у Al26, V50, Tc98, Ta180, Bi208, Np236 [14]. К этому изотопному составу можно добавить долгоживущий Еu152 (Т Ѕ= 13,542 лет). Возможно также предсказание долгоживущих изотопов гипотетического элемента с зарядовым числом 113 и массовыми числами 291, 292, 293, который должен обладать свойствами щелочного металла Е — Fr.
Следует отметить, что по нашей схеме можно предсказать свойства радиоактивных 34 элементов с Z > 110, а верхняя граница элементов равна (по нашему мнению) Z = 144 = F12 = 122. Математиками доказано, что во всем бесконечном ряду Фибоначчи нет, чисел кроме 1 и 144, которые являлись бы полными квадратами.
X. Интерпретация опытов Бакриса и Маневского 1996 г. Эти экспериментаторы установили в результате точных измерений, что на паладдиевом электроде (99,8% Pd), в слое толщиной 1 мкм, после продолжительного пропускания тока через электролит образовались следующие химические элементы: Mg (6,7%); Si (10,2%); Ca (19,9%); Тi (1,6%); Fe (10,5%); Zn (4,2%); Pd (31,9%); Pt (7,1%); Сl (3%); К (1,1%); Сu (1,9%); Аg (1,9%).
В работе [20] отмечается: «Можно ли после знакомства с этими данными говорить об ошибках, заблуждениях или некомпетентности? Эти результаты говорят сами за себя, и в дальнейшем аналогичные данные были получены многими исследователями. Огромный вклад в развитие этого направления внес итальянский физик Роберто Монти. Благодаря его работам появилась уверенность, что низкоэнергетическая трансмутация атомных ядер объективно существует. Главным препятствием на пути дальнейшего развития этого перспективнейшего научного направления является отсутствие физического и теоретического понимания сути происходящих при этом явлений».
Попытаемся дать эмпирическую интерпретацию вышеупомянутых экспериментов, только на основе предлагаемых новых расположений элементов.
а) В соответствии с экспериментами имеем 4 элемента с нечетным Z и 8 элементов с четным Z, т.е. «расщепление» 2:1;
б) С разделением зарядов нечет-четных конечных элементов имеем следующую «звезду» превращений:
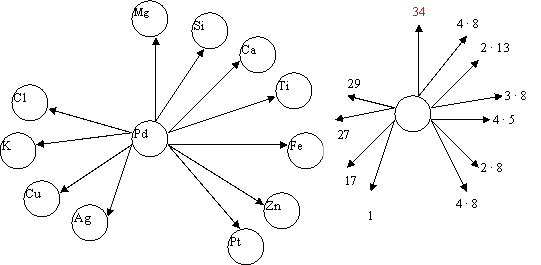
Справа от «звезды» элементов приведена соответствующая «звезда» приращений ∆Z, из которой видно, что в случае совпадения четности Z у исходного и конечных продуктов все ∆Z кратны или равны числам Фибоначчи 5, 8, 13, 34. Для Z — нечетных элементов приращения равны 1, 29 = 2 · 13 + 3 (число Люка – 2-ой аддитивный ряд: 2, 1, 3, 4, 7,…), ∆Z = 17= 2 · 8 + 1 (4-ый аддитивный ряд: 4, 1, 5, 6, 11, 17,…) и ∆Z = 27=2·13+1 (12 аддитивный ряд).
Заметим, что приращение 12-ого аддитивного ряда имеет минимальную концентрацию среди продуктов превращения (K — 1,1%).
в) Сумма зарядов н-ч ядер равна сумме зарядов ч-н ядер: Z = 2 · 17 + 2 · 19 + 2 · 29 + 2 · 47 = 12 + 14 + 20 + 22 + 26 + 30 + 78 = 8 · 28 = 224, т.е. для единичных атомов имеем «сохранение заряда»;
г) Число нуклидов н-ч природных ядер равно числу нуклидов ядер ч-н типа;
д) Средние заряды н-ч и ч-н ядер с учетом их процентного состава сохраняются с точностью 0,7%: Σ Zср = 2,163; Σ Zср = 2, 178.
После замеченных закономерностей естественно предположить, что в низкоэнергетических превращениях участвуют главным образом ядра с нечетной массой. Экспериментальное исследование на изотопный состав полученных элементов должно показать различие между естественным и изотопным составом конечных элементов. Очевидно, что это предположение легче всего проверить на определение процентного состава изотопа Pd105, которого в естественной смеси содержится 22,33%, а в микронном слое должен содержаться значительно более низкий (почти нулевой) процент Pd105.
Представляется, что, выявленное нами нормирование распределения химических элементов таблицы Менделеева аддитивным рядом Фибоначчи, открывает широкие возможности для предсказания новых свойств элементов, которые иногда играют решающую роль в процессе их использования. С позиций предлагаемой нами концепции закона распределения элементов по-новому могут быть интерпретированы их взаимоотношения в геологических процессах, участие их в комплексообразовании в ходе формирования минеральных парагенезисов или концентрации рудного вещества и т.д. Особенно многообещающим может оказаться использование новых геометрических позиций элементов в трехмерном пространстве. Авторы приводят только горизонтальные проекции пространственных спиралей (рис.1,3,4). Фронтальные проекции пространственных спиралей имеют по вертикали также «фибоначчиевую» структуру. В сущности, постоянно сталкиваясь с нерешенными проблемами в геохимическом поведении элементов, нами и была предпринята работа, результаты которой во фрагментарном изложении представлены в настоящей статье. Кроме того, фибоначчиевое распределение химических элементов и ядер, несомненно, облегчает открытие новых направлений в материаловедении и физике.
Очевидно, что за фенотипические расположения атомных ядер ответственны определенные генотипические факторы ядер, скрытые в их внутренней структуре. Из этого следует, что в основу множества исследований, например, геохимических процессов или минералообразования, так же как и рудообразования, вообще должна быть положена ядерная физика. Идя по этому пути, мы неизбежно придем к совершенно новому пониманию многих процессов и явлений, может быть, даже изменим свои представления о мироздании.
Литература
[1] В.К.Григорович «Металлическая связь и структура металлов» Москва, Издательство «Наука», 1988 г.
[2] Вавилов Н.С., Гавриченкова Т.Н. «Дублетно-концентрическая форма Периодической системы элементов Д.И.Менделеева» Москва, 1999 г.
[3] Ю.И. Кулаков Горно-Алтайская таблица химических мультиплетов KuFeRum г. Горно-Алтайск, 1999 г
[4] Румер Ю.Б., Фет А.И. «Группа Spin (4) и таблица Менделеева» Теоретическая и математическая физика— 1971 г., т.9, № 2, стр.203-10.
[5] «Система. Симметрия. Гармония» Москва, «Мысль», 1988 г., стр.210.
[6] Б. М.Кедров «Микроанатомия великого открытия» Москва, Издательство
«Наука»,1970 г.,стрЛ1,75.
[7] Ю.А.Шредер «Равенство, сходство, порядок» Москва, Издательство «Наука», 1971 г.
[8] В.И.Семишин «Периодическая система химических элементов Д.И.Менделеева» Москва, «Химия», 1972 г., стр.42.
[9] А. Лима-де-Фариа «Эволюция без отбора» Москва, «Мир», 1991 г.
[10] А.И.Гусев, А.А.Ремпель «Нанокристаллические материалы» Москва, «Физматлит», 2001, стр.117-122
[11] Г.Вейль «Симметрия», Издательство «Наука», Москва, 1968, стр. 33.
[12] А.В.Рыжаков «Математическая физика взаимодействий и течений», Москва, 2003, стр.384.
[13] Э.Ферми «Лекции по атомной физике» Москва-Ижевск, 2001, стр. 47.
[14] Физический энциклопедический словарь, Гос. научное издательство «Советская энциклопедия», Москва, 1962, т.2, стр. 148-149.
[15] О.Е.Акимов «Дискретная математика. Логика, группы, графы», Москва, Лаборатория Базовых знаний, 2003.
[16] « Химия и периодическая система» Редактор К.Сайто. Перевод с японского. Москва, «Мир», 1982, стр.129.
[17] Э.Г.Раков «Вещества и люди», ИКЦ «Академкнига», 2003, стр. 310.
[18] Н.А.Васютинский «Золотая пропорция», Москва, «Молодая гвардия», 1990.
[19] Ферсман А.Е. «Пегматиты СССР», Москва-Ленинград издательство АН СССР, 1936 г.
[20] В.И.Ильин «Нейтрино и физические основы энергетики будущего», Москва, 2003, стр.124.
рис.1 – Атомы; | ||
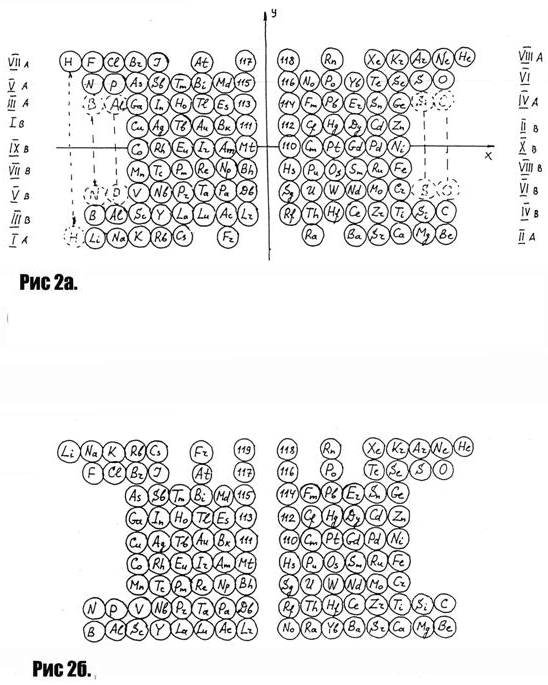
рис.2 – а) парная (двурядная) модель по нечетным ионизационным потенциалам, б) парная (двурядная) модель по четным ионизационным потенциалам; | ||
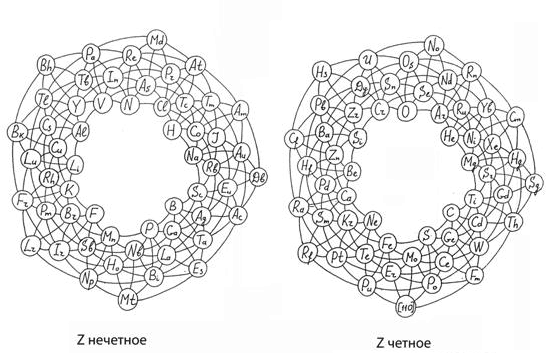
рис.3 – а) спиральная модель, соответствующая нечетным по Z элементам; б) спиральная модель, соответствующая четным по Z элементам; | ||
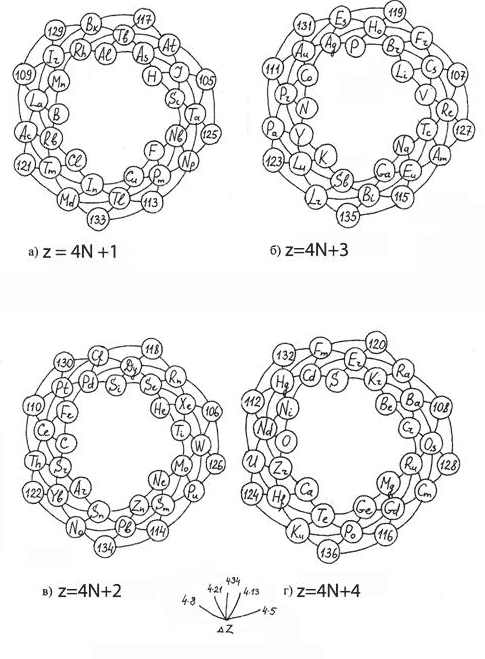
рис.4(а,б,в,г) – спиральные расположения элементов, сгруппированные по признакам Z = 4 К + i; i = 1, 2, 3, 4. | ||
рис. 5 – парные элементы на сфере Лобачевского |
Н.А. Шило, А.В. Динков, Фенотипическая система атомов в развитие идей Д.И.Менделеева // «Академия Тринитаризма», М.,
|
|