Работа посвящена проблемам эволюции открытых систем в микро- и макромире. Исследования открытых диссипативных систем естественного и искусственного происхождения привели к открытию существующей закономерности и обоснованию закона самоорганизации сложных систем переработки вещества, энергии, информации.

Следует ожидать, что в процессе эволюции все системы естественного и искусственного происхождения с их подсистемами образуют экологические цепочки древа развития, структурированные в соответствии с законом «самонормирования».

Рассмотрение было начато с систем мельниц — первых машин созданных человеком, послуживших основой развития промышленности, что отмечалось еще К.Марксом.

В течение тысячелетий мельницы являлись объектом внимания и исследования бесчисленной армии исследователей: ученых и аспирантов. Нет ничего удивительного, если система машин-мельниц в настоящее время близка к предельной оптимизации, как следствие эмпирического совершенствования, имеющего целью минимизировать затраты труда, энергии, металла и других материалов на единицу измельченного продукта. Исследования в области теории мельниц — науки о методах решения минимаксных задач о семействе, цепочке и типаже мельниц, подтверждают вышеизложенное.

Таким образом, семейство мельниц — множество машин и аппаратов различных конструкций и методов воздействия на твердые материалы при их измельчении, сопровождающемся генерацией новой поверхности, характеризуется экологической цепочкой, образованной по возрастающей интенсивности потока энергии, диссипируемой в мельнице – энергонапряженности, дискретные значения которой, усредненные по нишам, образуют последовательность членов геометрической прогрессии семейство мельниц — последовательность мельниц различных конструкций.

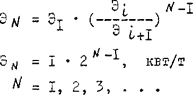
Примером действия закона самонормирования является также последовательность чисел Фибоначчи. Закон образования этих чисел

В тоже время, с увеличением порядкового номера числа, отношение двух соседних чисел стремится к пределу

что позволяет представить их ряд в виде последовательности членов геометрической прогрессии

Нахождение учеными, представляющими различные естественные науки, этой числовой закономерности в объектах живой природы и использование этой последовательности чисел в процессе создания произведений архитектуры позволило создать высокие образцы зодчества и строительного мастерства. Эти соотношения вошли в историю архитектуры как правило «золотого сечения». Известно, что этой последовательности подчинены, например, процессы размножения биологических популяций, а также творения природы в растительном мире.

В.И. Вернадский в своих «Размышлениях натуралиста» рассматривает как одно из самых глубинных свойств пространства — времени его асимметрию: «Учение о симметрии разработано, главным образом, минерологами и математиками. Но в кристаллографии симметрия проявляется не во всей полноте. На это еще давно указывал Пьер Кюри. Особенно ярко это проявляется для наук биологических, что видно хотя бы из одного факта: ось симметрии 5-го порядка, неразрывно связанная с «золотым» или «божественным» сечением, отражающемся в нашем осознании красоты,— мысль, занимавшая Леонардо да Винчи, Иоганна Кеплера и всех других, к ней подходивших,— эта ось, играющая заметную роль в морфологии форм жизни, в кристаллографии невозможна. И она действительно в ней отсутствует».

Упоминание В. И. Вернадским «золотого» сечения восходит в своей истории к эпохе математической школы пифагорейцев. Ими была решена следующая задача: если разделить любой отрезок на две части «А» и «Б» так, чтобы:

то при решении этого квадратного уравнения получаются два корня

Эти числа и получили название «золотых». Они действительно замечательные. Везде, где человек ощущает гармонию — в звуках, в цвете, в размерах, — всюду присутствует «золотое» число. Огромна роль его в архитектуре и живописи.

Еще пифагорейцы заметили, что музыкальный звукоряд построен по закону соотношений частот, равных «золотому» числу. Спустя много веков итальянский математик XVI века Фибоначчи построил математический ряд (0, 1, 2, 3, 5, 8, 13, 21, 34, 55...), описывающий процесс размножения кроликов, т.е. сугубо биологический процесс. Можно обнаружить закон формирования такого ряда: член ряда, начиная с четвертого, равен сумме двух предыдущих членов. Если же в таком ряде взять отношение последующего члена к предыдущему или наоборот, то получим уже знакомые нам числа: 1,618 и 0,618. Причем, чем больше порядковые номера членов, тем точнее выполняется «золотое» соотношение. Числа этого ряда так и называются — числа Фибоначчи.

Через сто лет Кеплер создал свою модель солнечной системы, уже зная основные размеры планет, периоды их обращения и взаимные расстояния. К его изумлению, вес эти числа оказались числами Фибоначчи. Оказалось, что наш ближний космос организован по законам музыкальной гармонии. Все это Кеплер изложил в своей книге «Музыка сфер». Кроме того, оказалось, что «золотое» число тесно связано с живой природой. Оно присутствует в телах, имеющих пять осей симметрии, т.е. в «пентасистемах». Уже отмечалось, что в неживой природе, в кристаллографии наблюдаются самые различные кристаллы с любым числом осей симметрии, кроме пяти. Живая материя — вся построена по принципу пентасистемы. Она как бы дополняет мир камней и кристаллов.

Даже вирус, снятый электронным микроскопом, имеет форму правильного пятигранника. То же можно сказать о морских звездах и цветах. Когда недавно были замерены гравитационные биения, испытываемые Землей из-за эксцентриситета орбит других планет, то оказалось, что они представляют собой гармонический музыкальный аккорд. Еще более удивительно присутствие «золотого» числа в человеке. Так, дельта-ритмы мозга на реакцию раздражителя представляют собой затухающие апериодические колебания, соседние периоды которых соотносятся по закону «золотого» сечения.

Ученые давно обратили внимание на то, что все органы чувств имеют логарифмический закон чувствительности. Именно благодаря ему динамический диапазон восприятия света, звука и т. п. огромен. Но в традиционной математике вычисление логарифма представляет собой трудную задачу.

Удивительным фактом является и то, что наша планета — пентасистема. По последним представлениям, Земля — это кристалл, имеющий форму додекаэдра, вложенного в косаэдр.

Возникло сомнение в том, что живая природа построена по принципу десятичной математики. Откуда взялось основание «10», станет совершенно понятным, если мы взглянем на наши пальцы.

Однако, математику можно создать по любому основанию. Например, вся вычислительная техника использует математику, созданную по основанию «2». А что если создать «золотую» математику — по основанию 1,6187. Результат оказался поразительным: в такой математике вычисление логарифма — элементарная арифметическая операция, т.е. мир живой материи создан по «золотой» математике,

а «золотое» сечение, очевидно, является одним из фундаментальнейших принципов самоорганизации материи.

Именно это обуславливает приемлемость ряда чисел Фибоначчи для описания системотехнических процессов.

Приведенные примеры можно было бы легко умножить, однако это вряд ли было информативным. Более интересно расширить масштаб системы и включить в нее в качестве элемента Землю и ее биологические характеристики, поскольку они описываются биогеохимическим законом В.И.Вернадского.

В шкале геологического летоисчисления по Д.Хексли легко заметить, что и этот параметр, характеризующий эволюцию Земли, подчинен закону самонормирования.

Изложенное позволяет перейти в соответствии с идеями В.И.Вернадского к рассмотрению эволюции систем «человек-машина», т.е. типажей, цепочек и видов машин, а затем их иерархических сообществ — отдельных отраслей промышленности и экономики в целом.

В процессе работы над теорией мельниц и теорией измельчения выявлены более общие закономерности материального мира (макромира), которым подчиняются эволюционирующие системы переработки вещества, энергии, информации.

Дальнейшее исследование этой проблематики привело к теоретическому обоснованию закономерностей структурирования кибернетических систем преобразователей потоков вещества, энергии и информации.

Указанная закономерность выражается в образовании для систем с «сухим» трением параметрических рядов, представляющих собой последовательность членов арифметической прогрессии; для систем с «вязким» трением — последовательность членов геометрической прогрессии. Последние образуют гиперболические распределения: три фундаментальных асимптотических распределения Колмогорова и высшие гармоники.

Фундаментальные распределения характеризуются показателями степени m = 1/2; 2/2; 3/2.

Эти распределения известны в статистике как эмпирические распределения Уилисса, Коши и Хольцмарка.

Для решения задачи предложен метод, получивший позднее название «адаптированного моделирования».

Сущность метода заключается в гипотезе о квази-оптимальном состоянии конкретной анализируемой системы преобразователей.

Это существенно сокращает разнообразие системы и переводит ее из состояния неопределимости в состояние определимости. Предложен компактный когерентный код, составленный из конкретных параметров системы.

Основными и производными параметрами системы являются: поток энергии, диссипируемый в преобразователе; поток, подвергающийся преобразованию; вес преобразователя и его размеры.

Производные параметры: интенсивность потока энергии, диссипируемой в преобразователе — его энергонапряженность; интенсивность преобразуемого потока — удельная производительность преобразователя; цена преобразования — денежное выражение стоимости преобразования единицы потока, выраженное через затраты энергии на преобразование единицы потока.

Затраты энергии на преобразование единицы потока определяют его прочность. Последняя не является физической константой, так как зависит от конструкции преобразователя и режима его работы.

Кроме того, прочность характеризуется различной размерностью, в зависимости от вида преобразуемого потока: для вещества — это затраты энергии на образование единицы новой поверхности [ Дж/м² ]; для энергии [ Дж/Дж ]; для информации [ Дж/бит ].

Предлагается назвать единицу прочности «Ребиндер» в память о заслугах в этой области академика П.А. Ребиндера.

Проведен анализ широкого класса систем преобразователей потоков вещества, энергии и информации.

Основное внимание уделено преобразователям твердых веществ — мельницам, которые в силу своей длительной истории с наибольшей вероятностью являются квази-оптимальными.

Установлено, что основные и производные параметры этой системы, а также других систем преобразователей образуют распределения Уилисса, Коши и Хольцмарка.

Процесс эволюции системы преобразователей рассматривается как антагонистическая игра Бюффона с вероятностью опознания оптимального варианта адаптации, равного (p /2)^-1 для монотонно убывающих параметрических рядов, а для монотонно возрастающих рядов, равного p /2.

Рассматривая эту вероятность как знаменатель прогрессии соответствующих распределений, получаем три фундаментальных распределения Колмогорова:

Общим теоретическим обоснованием предложенной теории являются принцип наименьшего действия Гаусса, а также теоремы Рамсея и Винера.

Полученные решения интерполируются и экстраполируются, то есть отвечают требованиям, предъявляемым к научной теории.

Метод приложим к анализу эволюционирующих систем искусственного и естественного происхождения, в том числе, для диссипативных неравновесных систем, рассмотренных И.Р. Пригожиным.

Резюме: Все вышеизложенное позволяет с достаточной степенью уверенности утверждать о существовании объективной закономерности, нормирующей биогеохимическую эволюцию. Аналитическое выражение этих процессов — плотная дискретная последовательность значений характерных параметров эволюционирующих систем, представляющих последовательности членов геометрической прогрессии;

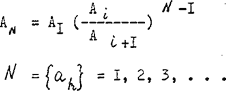
отличается эквидистантностью устойчивых или оптимальных значений параметров на плоскости (lg А_N, N), поскольку

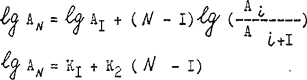
Перейдем к физической интерпретации установленного закона самонормирования.

Аналитические выражения топологических рядов параметров таких систем являются минимаксными решениями задач об их оптимальных управлениях — основных задач теории преобразователей.

Другими словами, процесс оптимизации при адаптации систем преобразователей к внешней среде является статистическим выражением принципа экстремального действия.

Таким образом, всякая система преобразователей в процессе адаптации к внешней среде, подчиненном минимизации удельных затрат вещества, энергии и информации на единицу преобразуемого потока, нормируется, образуя дискретный ряд характеристических показателей систем преобразователей потоков — эквидистантных на логарифмической плоскости функционалов.

Ряды эти представляют последовательности членов геометрической прогрессии, если система адаптируется к среде с вязким трением и последовательность членов арифметической прогрессии — если трение среды сухое.

Существование объективного закона самонормирования систем преобразователей потоков под действием принципа экстремальности исключает возможность доказательства постулата Фейнмана, представляющего одну из формулировок закона самонормирования.

Изложенное позволяет установить аналогию между машинами-преобразователями потоков вещества, энергии и информации и биологическими преобразователями (см. приложение I). Приведенный на рис.35 график подтверждает высокую степень эволюционной оптимизации преобразователей потоков в соответствии с законом самонормирования.

Таким образом, закон самонормирования позволяет обобщить различные проявления эволюции систем, описанные законами Вернадского, Дарвина, Тициуса-Боде, фон Кармана-Габриэлли и интерпретировать эволюцию как колебательный процесс, минимизирующий свободную энергию систем преобразователей потоков вещества, энергии и информации.

Эволюция сложных систем трактуется как последовательность переходов в иерархии структур возрастающей сложности, причем отбор идет в условиях возрастающей диссипации, тогда как любое стационарное состояние удовлетворяет принципу минимума возрастания энтропии [ 1 ].

Принцип самоорганизации (построения сложного из простого) предполагает, что простыми и примитивными операциями, последовательно повторенными, достигается получение необычайно сложных объектов.

Преодолеть сложность описания сложных систем можно с помощью некоторых объективных математических законов. Геометрическая прогрессия – один из них: из простого очень быстро получается сложное.

«Оптимум» сложности систем – изюминка метода самоорганизации и крупное достижение науки.

Теория регулирования рассматривает системы, описываемые дифференциальными уравнениями, мало чем отличающимися от уравнений колебания маятника. Если такая система состоит из пяти–шести уравнений, то она может быть промоделирована пятью-шестью взаимосвязанными «маятниками».

Классические приемы исследований изучают «королевства маятников», каждый из которых математически точно описывается, так как разработана очень точная математическая теория всякого рода колебательных процессов.

При анализе экологических систем, которые относятся к категории сложных, целесообразен комбинированный метод: точные данные закладываются в модель в начале моделирования, неизвестное – удел самоорганизации. Суть метода анализа: сложная система разбивается на подсистемы до тех пор, пока не получим подсистемы, которые описываются моделями, доступными для решения на ЭВМ и обозримыми для экспериментатора [ 2 ].

В процессе анализа «теории сложных систем» и ее применения в системотехнике и экологии разработаны три метода описания сложных систем: метод потенциальной эффективности самоорганизующихся моделей, комбинированный метод и метод имитационного моделирования.

Общий вывод анализа таков: сложным системам свойственно умение приспосабливаться к окружающей среде – адаптивность, способность менять свою структуру рациональным целесообразным образом, то есть самоорганизация [ 3 ].

У сообществ различной природы (животных, растений, машин, аппаратов и т.д.) структура однотипна. Все это относится к системам, созданным при ограниченности ресурсов и стремящимся как можно лучше их использовать, — таков всеобщий закон естественного и искусственного отбора.

В процессе совершенствования техники происходит своеобразный информационный отбор, похожий на естественный отбор в природе, который осуществляется человеком, но отражает объективные процессы [4].

Синергетика – область науки, которая занимается изучением эффекта самоорганизации в физических системах, а также родственных им явлений в более широком классе систем.

В физике явления самоорганизации просматриваются, начиная с атомарного уровня и вплоть до галактик – образований астрономического масштаба.

Системы, находящиеся вдали от термодинамического равновесия, могут обмениваться с окружающей средой не только энергией, но и массой вещества. Такие системы, в отличие от замкнутых, называют открытыми.

Энергия в них может рассеиваться и необратимым образом переходить в другие виды энергии, например, в энергию колебательного или теплового движения атомов. Такие системы называются диссипативными.

В настоящее время известно большое число неравновесных физических процессов, в которых возникают эффекты самоорганизации, приводящие к образованию структур, упорядоченных в пространстве и во времени.

Синергетика пытается найти общие методы для описания того, как возникают и развиваются упорядоченные структуры в открытых системах вдали от равновесия.

При научном объяснении мироздания необходимо показать, как законы природы приводят к появлению определенного порядка из первоначального хаоса и затем к усложнению и развитию образовавшихся упорядоченных структур.

Очевидно, что существует общий подход к описанию динамических коллективных явлений в многокомпонентных системах, обладающих свойством самоорганизации; то есть появление определенного порядка в однородной массе, последующего совершенствования и усложнения возникшей структуры. Именно для того, чтобы выработать такой подход, который имел бы возможность приложения к самым различным явлениям в разных научных дисциплинах, под синергетикой предложено понимать область науки, которая занимается изучением эффектов самоорганизации в физических системах, а также родственных им явлений в более широком классе систем.

Ученые разных отраслей знаний, занимающиеся проблемами появления и развития порядка в сложных динамически развивающихся системах, обнаруживают родственные черты в многочисленных проявлениях функционирования этих систем. В процессе анализа этих явлений образовалось направление в науке, которое исследует упорядоченные структуры, в первую очередь, неравновесные системы, в которых неравновесность задается не начальными условиями, а поддерживается на протяжении всего процесса, например, за счет: неоднородности распределения температуры и состава вещества по объему, с потоками вещества внутри системы и с более сложными типами неравновесности за счет воздействия различных полей.

Процессы самоорганизации происходят при участии большого числа взаимодействующих элементов благодаря проявлению их совместного кооперативного воздействия.

Таким образом, класс процессов и явлений, которые охватывает синергетика, достаточно широк: сюда относятся физические, химические, биологические и другие искусственные и естественные сложные системы.

Синергетика обращает внимание на то, что эффекты упорядочения, которые возникают в динамических системах, обязаны своим появлением действию различных нелинейных процессов.

Подход к анализу динамики появления неравновесных структур, способных к самоорганизации, объясняемый с позиций синергетики, расширяет методы исследования динамических систем, различных по своей природе.

Развитие и совершенствование поиска закономерностей явлений самоорганизации само по себе составляет одну из целей, которые ставит перед собой синергетика [ 5, 6, 7, 8, 9 ].

В последнее время одним из самых модных подходов к исследованию динамических процессов является теория «хаоса». Точного математического определения понятия «хаоса» пока не существует. Сейчас зачастую хаос определяют как крайнюю непредсказуемость постоянного нелинейного и нерегулярного сложного движения, возникающую в динамической системе.

Однако следует отметить, что хаос не случаен, несмотря на свойства непредсказуемости. Более того, хаос динамически детерминирован (определен). На первый взгляд, непредсказуемость граничит со случайностью – ведь мы, как правило, не можем предсказать, как раз, случайные явление. Непредсказуемость хаоса объясняется существенной зависимостью от начальных условий.

Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамического система после некоторого числа итераций зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как называют — аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемое конечное состояние. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов.

Алгебраические фракталы, с большой точностью описывающие многие физические явления и образования реального мира со сложной геометрической формой объектов, аналитически и графически описывают с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы.

Интерпретируя нелинейный итерационный процесс как дискретную динамическую систему можно пользоваться терминологией теории эволюции этих систем: «фазовый портрет», «установившийся процесс», «аттракторы», «фракталы».

Обычно считают, что хаос является более высокой формой порядка, однако более правильно считать хаос другой формой порядка – с неизбежностью в любой динамической системе за порядком в обычном его понимании следует хаос, а за хаосом порядок. Если мы определим хаос как беспорядок, то в таком беспорядке мы обязательно сможем увидеть свою, особенную форму порядка.

Движение от порядка к хаосу и обратно, по всей видимости, является сущностью вселенной, какие бы проявления ее мы не изучали. Даже в человеческом мозгу одновременно присутствует упорядоченное и хаотическое начала. Первое соответствует левому полушарию мозга, а второе — правому. Левое полушарие отвечает за сознательное поведение человека, за выработку линейных правил и стратегий в поведении человека, где четко определяется зависимость «если..., то..».. В правом же полушарии царит нелинейность и хаотичность. Интуиция является одним из проявлений правого полушария мозга.

Теория хаоса изучает порядок хаотической системы, которая выглядит случайной, беспорядочной. При этом теория хаоса помогает построить модель такой системы, не ставя задачу точного предсказания поведения хаотической системы в будущем.

Первые элементы теории хаоса появились ещё XIX веке, однако подлинное научное развитие эта теория получила во второй половине XX века, вместе с работами Эдварда Лоренца (Edward Lorenz) из Массачусетского технологического института и франко-американского математика Бенуа Б. Мандельброта (Benoit B. Mandelbrot).

Эдвард Лоренц в свое время (начало 60-х годов XX века, работа опубликована в 1963 году) рассматривал, в чем возникает трудность при прогнозировании погоды. До работы Лоренца в мире науки господствовало два мнения относительно возможности точного прогнозирования погоды на бесконечно длительный срок.

Первый подход сформулировал еще в 1776 году французский математик Пьер Симон Лаплас. Лаплас заявил, что «... если мы представим себе разум, который в данное мгновение постиг все связи между объектами во Вселенной, то он сможет установить соответствующее положение движения и общие воздействия всех этих объектов в любое время в прошлом или в будущем".

Этот его подход был очень похож на известные слова Архимеда: «Дайте мне точку опоры, и я переверну весь мир». Таким образом, Лаплас и его сторонники говорили, что для точного прогнозирования погоды необходимо только собрать больше информации обо всех частицах во Вселенной, их местоположении, скорости, массе, направлении движения, ускорении и т.п. Лаплас думал, чем больше человек будет знать, тем точнее будет его прогноз относительно будущего.

Второй подход к возможности прогнозирования погоды раньше всех наиболее четко сформулировал другой французский математик, Жюль Анри Пуанкаре. В 1903 году он сказал: «Если бы мы точно знали законы природы и положение Вселенной в начальный момент, мы могли бы точно предсказать положение той же Вселенной в последующий момент. Но даже если бы законы природы открыли нам все свои тайны, мы и тогда могли бы знать начальное положение только приближенно. Если бы это позволило нам предсказать последующее положение с тем же приближением, это было бы все, что нам требуется, и мы могли бы сказать, что явление было предсказано, что оно управляется законами. Но это не всегда так; может случиться, что малые различия в начальных условиях вызовут очень большие различия в конечных явлениях. Малая ошибка в первых породит огромную ошибку в последних. Предсказание становится невозможным, и мы имеем дело с явлением, которое развивается по воле случая».

В этих словах Пуанкаре мы находим постулат теории хаоса о зависимости от начальных условий. Последующее развитие науки, особенно квантовой механики, опровергла детерминизм Лапласа. В 1927 г. немецкий физик Вернер Гейзенберг открыл и сформулировал принцип «неопределенности». Этот принцип объясняет, почему некоторые случайные явления не подчиняются детерминизму Лапласа. Гейзенберг показал принцип неопределенности на примере радиоактивного распада ядра атомов. Так, из-за очень малых размеров ядра невозможно знать все процессы, происходящие внутри его. Поэтому сколько бы мы не собирали информации о ядре, точно предсказать, когда это ядро распадется невозможно.

Какими же инструментами располагает теория хаоса. В первую очередь, это аттракторы и фракталы.

Аттрактор – геометрическая структура, указывающая на устойчивое поведение системы в фазовом пространстве по прошествии длительного времени.

Фазовое пространство – это абстрактное пространство, координатами которого являются степени свободы системы. В частности, у движения маятника две степени свободы. Это движение полностью определено начальной скоростью маятника и положением маятника в пространстве. Если движению маятника не оказывается сопротивления, то фазовым пространством будет замкнутая кривая. В реальности на Земле на движение маятника оказывает влияние сила трения. В этом случае фазовым пространством будет спираль.

К хаосу системы могут переходить разными путями. Среди последних выделяют бифуркации, которые изучает теория бифуркаций.

Бифуркация представляет собой процесс качественного перехода от состояния равновесия к хаосу через последовательное очень малое изменение определенных параметров, то есть происходит катастрофический скачок, качественно изменяющий свойства системы.

Таким образом, хаос может возникнуть через бифуркацию, что показал Митчелл Фейгенбаум (Feigenbaum). При создании собственной теории о фракталах Фейгенбаум, в основном, анализировал логистическое уравнение.

X_n+1 = (C+1)^.X_n – C^.(X_n)²,

где С — внешний параметр, откуда следует, что при некоторых ограничениях во всех подобных уравнениях происходит переход от равновесного состояния к хаосу.

Отсюда следует вывод — заключительным состоянием физических эволюционирующих систем является состояние динамического хаоса.

Таким образом, состояние системы в момент бифуркации является крайне неустойчивым и бесконечно малое воздействие может привести к выбору дальнейшего пути движения, а это, как мы уже знаем, является главным признаком хаотической системы, т.е. наблюдается существенная зависимость от начальных условий и параметров процесса.

Фейгенбаум установил универсальные закономерности перехода к динамическому хаосу при удвоении периода, которые были экспериментально подтверждены для широкого класса механических, гидродинамических, химических и других систем.

Фактически первый переход от стабильности к видимой форме упорядоченности, но уже изменчивости, происходит в первой точке бифуркации; далее количество бифуркаций увеличивается, достигая огромных величин, что приводит к образованию хаоса.

Таким образом, с помощью теории бифуркаций можно предсказать характер эволюции сложных систем, возникающий при переходе системы в качественно иное состояние, а также оценить область существования стабильности и оценить ее устойчивость.

Рождение фрактальной геометрии связано с выходом в 1977 г. книги Мандельброта «Фрактальная геометрия природы», который совершил кардинальный прорыв в науке, предложил реализовать на комплексной плоскости простейший нелинейный алгоритм в виде:

Zn+1 → Z2n + C  [Стрелка (→) означает итерацию]

(2).

Этот алгоритм позволяет получит числовую последовательность, каждый член которой равен квадрату предыдущего плюс некое слагаемое. Точки этой последовательности на графике будут лежать не на прямой, а в плоскости.

Однако, если в итерационном процессе (2) зафиксировать Z₀ и изменять С, то получаем множество Мандельброта. Прибавляя константу С к квадратичному процессу и полагая первоначально Z = 0, можно получить стабильные итерации и график функции – удивительную фигуру, известную во всем мире под именем «фрактал Мандельброта» [10].

Формула кратко суммирует множество результатов Мандельброта, полученных благодаря фрактальной геометрии природы мира и четвертому измерению.

Простейшая модель итерации – последовательность суммирования, известная как ряд Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13 и т.д. В этом удивительном ряду результат деления каждого последующего числа на предыдущее асимптотически приближается к трансцендентному числу 1,6180339, выражающему пропорцию «золотого» сечения. Мир буквально наводнен этим соотношением: все удивительные творения в мироздании, включая и человека, соответствуют правилу «золотого» сечения. Это исключительно важный момент в структуре мироздания: оказалось, что именно алгоритмом Мандельброта пользуется природа, создавая свои шедевры – фракталы «золотого» сечения – от листа травы до биологической популяции.

В 1993 г. в России вышла книга Рихтера и Пайтгена «Красота фракталов», в которой подведены итоги результатов исследования в области фрактальной геометрии: «Мы обнаружили там фантастический мир, богатство форм которого контрастирует почти на грани абсурда с простотой формулы Z_n+1 → Z²_n + C». Фрактальный бум охватил всю планету и стал одной из примет науки конца второго тысячелетия [11].

Удивительная простота фрактальных алгоритмов и потрясающее великолепие их форм сделали фрактальную геометрию необычайно эффективным орудием для описания морфологических свойств природы, подтверждая афоризм «мудрость в простоте». Принцип «единого простого», задающего «разнообразное сложное», можно проследить в устройстве всего мироздания. Этот принцип заложен в геноме человека и животных, когда одна клетка живого организма содержит всю информацию обо всем организме в целом.

Общим для всех типов фрактальных структур является их самоподобие – основное свойство, обеспечивающее выполнение в фракталах основного закона природы – Закона единства в многообразии мироздания.

Гармония порядка и беспорядка, космоса и хаоса, по-видимому, есть один из высших принципов природы.

Крупнейшие ученые современности И.Пригожин, Б.Мандельброт, С.Смэйл и Хенон обнаружили, что на границе между конфликтами противоборствующих сил стоит не рождение хаотических структур, как считалось ранее, а происходит возникновение самоорганизации, порядка более высокого уровня. Структура этой самоорганизации не статична, а постоянно изменяется. Судя по всему, организация этого порядка применима ко всему – от динамических механических систем до экономического рынка. При этом фрактальные структуры, установленные учеными, выступают неким пограничным образованием, позволяющим исследовать взаимосвязь явлений хаоса и порядка в макромире.

Литература

1. Николис Г., Пригожин И. Самоорганизация в неравновесных системах. – М.: Мир, 1979.
   
2. Левитин К. Вдали от королевства маятников // Знание-сила. – 1980. — № 5.
   
3. Материалы школы-семинара «Теория сложных систем и ее применение в системотехнике и экологии». Ин-т кибернетики АН УССР / Под ред. Беляева В.И., Флейшмана Б.С., Ивахненко А.Г., Котова Г.И.
   
4. Угроза многообразия изделий // Знание-сила. – 1980. — № 5.
   
5. Кадомцев Б.Б., Рязанов А.И. Что такое синергетика // Природа. – 1983. — № 8.
   
6. Хакен Х. Синергетика. – М.: Мир, 1980.
   
7. Гапонов-Грехов А.В., Рабинович М.И. Хаотическая динамика простых систем // Природа. – 1981. — № 2.
   
8. Синай Я.Г. Случайность неслучайного. // Природа. – 1981. — № 3.
   
9. Кочевых И.П. Главный Закон Вселенной. – Винница: Антекс, 2001. — 48 с.
   
10. Мандельброт Бенуа. Фрактальная геометрия природы, 1977.
    
11. Рихтер, Пайтген Х.-О. Красота фракталов, 1993.
    
12. Зельдович Я,Б., Соколов Д.Д. Фракталы, подобие, промежуточная асимптотика (успехи физических наук), 1985. – 146. – Вып. 3. — С. 493-506.
    
13. Ильяшенко Ю.С., Четаев А.Н. О размерности аттракторов одного класса диссипативных систем (прикладная математика и механика)., 1982. – 46 — № 3. — С. 374-381.
    
14. Фракталы в физике: Труды VI международного симпозиума по фракталам в физике. – Триест, 9-12 июля 1985 г. – М.: Мир, 1988. – 672 с.
    
15. Працевитый Н.В. Распределение случайных величин с независимыми Q-символами (асимптотические и прикладные задачи случайных эволюций). – Киев. Ин-т математики АН Украины, 1990. – С.92-101.
    
16. Акунов В.И., д.т.н. (г.Москва), Чечик А.Л. (г.Киев). Математическое моделирование больших систем преобразований потоков вещества, энергии, информации // Сб. Эволюция открытых систем. – 2003. – Киев.
    
17. Акунов В.И. Самоорганизация сложных систем / Заявка на открытие. – 1975.