Несмотря на то, что интерес к проблеме золотого сечения в настоящее время по-прежнему нарастает, тем не менее, пока еще не создана теория золотого сечения в той постановке, которая воспринимается официальной наукой. Имеется ввиду, прежде всего, что пропорции золотого сечения должны быть решением некоторой оптимизационной задачи, где присутствует некий критерий оптимизации, который обычно минимизируется. Пока такая задача для золотого сечения еще не сформулирована. Поэтому мы наблюдаем с одной стороны пренебрежение к феномену золотого сечения со стороны официальной науки, а с другой, несмотря на это пренебрежение, – активный процесс накопления фактов его проявления в природных явлениях и человеческой деятельности.

В данной статье предлагается один из таких фактов. Рассматривается задача оценки зависимости энтропии системы, элементы которой имеют биномиальный закон распределения

1 = (p + q)n

(1)

от величины n, где p > 0, q > 0, q + p = 1.

Данный закон выбран по той причине, что такие фундаментальные распределения гауссового класса, как нормальный, Пуассона, Паскаля, Пойа вытекают из биномиального распределения [1].

Так, если формулу (1) при p = q = 0,5 разложить по правилу бинома Ньютона, то получится обычный нормальный закон распределения со средним m = 0,5. Причем, как видно и графика на рис.1, форма кривой нормального распределения зависит от параметра n.

Рис.1. Форма кривой нормального распределения для различных значений n.

Зададимся вопросом, как изменяется энтропия биномиального распределения в зависимости от степени n.

В качестве энтропийной меры выберем формулу, предложенную в [2]:

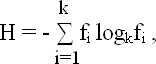(2)

где f_i – вероятность i-го события,

Данная формула отличается от формулы, предложенной Шенноном в 1948 году, основанием логарифма. У Шеннона основание логарифма равно 2. Здесь оно равно k, что позволяет представить Н как величину, нормированную на единицу. Если энтропия является, как принято считать, мерой хаоса, то ее дополнение до единицы есть мера порядка, а их сумма, соответственно, равна единице.

Из равенства:

следует, что мера порядка равна

Воспользуемся формулой (2) для оценки зависимости энтропии распределения (1) от степени n.

Для расчетов возьмем следующие значения параметров p и q:

В качестве значений n примем 10, 100, 150, 200, 250, 300, 350, 400, 450 и 500.

В результате проведенных расчетов получается семейство зависимостей, представленных на рис.2.

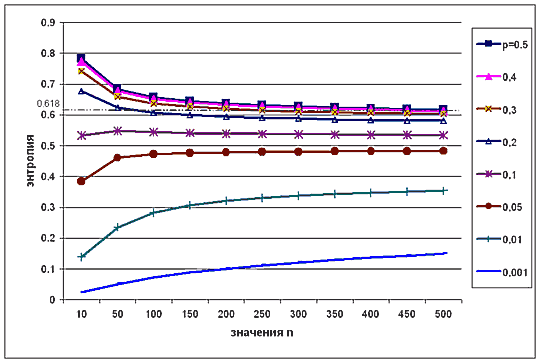
Рис. 2. Зависимость энтропии биномиального распределения от величины n

При рассмотрении полученных графиков следует, что:

1. при увеличении n и при p = q = 0,5 величина энтропии асимптотически стремится к величине 0,618, то есть к пропорции золотого сечения;
2. при увеличении n и уменьшении отношения p:q значения энтропии становятся меньше величины 0,618;
3. при отношении p:q ≈ 0,1:0,9 значение энтропии практически не зависит от величины n.
4. при увеличении n и отношениях p:q < 0,1:0,9 значения энтропии монотонно увеличиваются и стремятся к горизонтальным асимптотам.

Используя данные графика рис. 2, можно построить график зависимости значений горизонтальных асимптот (при n> ∞) от величины p. Получаем монотонно убывающую от точки золотого сечения 0,618 до 0 зависимость, представленную на графике рис. 3.

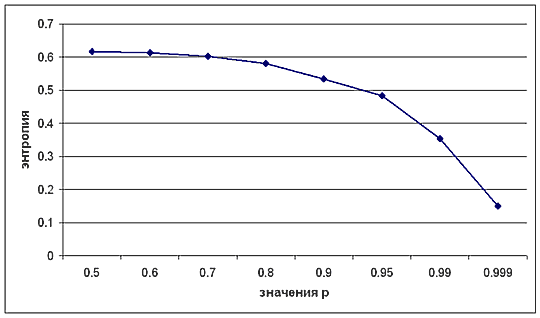
Рис.3. Зависимость значений горизонтальных асимптот от величины p

Таким образом, если система состоит из n элементов, имеющих биномиальное распределение, то из представленных расчетов следует, что:

• для слабо структурированных систем (при значениях 0,:0,9 < p:q ≤ 1) увеличение числа n способствует процессу самоорганизации системы (а при p:q = 1 — стремлению энтропии к золотому сечению),
• для сильно структурированных систем (при значениях 0 < p:q < 0,1: 0,9) увеличение числа n способствует процессу хаотизации системы.

• 
  

То есть увеличение числа элементов может как структурировать систему, так и хаотизировать ее. Все зависит от первоначального уровня структурированности или хаотизированности этой системы.

Получается так, что при определенных условиях хаос может «самоструктурироваться», а структура – «самохаотизироваться».

1. Корн Г. и Корн Т. Справочник по математике для научных работников и инженеров. М., Наука, 1973.
2. Харитонов А.С. Минимальное число параметров, характеризующих социально-экономическое развитие регионов // Аудит и финансовый анализ. 2002. №1. С.193-208.