|
|
|
Scott A. Olsen
Раскрытие Второго Принципа Платона.
(Перевод, Предисловие и комментарии А.П. Стахова)
Можно по разному относиться к изучению «первоисточников», к каким по праву принадлежат труды величайшего греческого философа Платона. В некоторых сочинениях современных исследователей делается попытка доказать, что Пифагор, Платон, Евклид (и даже Леонардо да Винчи) не знали о «Золотом Сечении», а само «Золотое Сечение» не играло никакой роли в греческой культуре и культуре Возрождения. Такой вывод делается на основании анализа «первоисточников», то есть трудов Платона, Аристотеля, Евклида, Леонардо да Винчи и других гениев эпохи Древней Греции и Возрождения.
Но можно к изучению трудов Платона подойти по-другому, а именно так, как это сделал американский философ Скотт Олсен в своей статье «Неопределенная Двоица и Золотое Сечение: Раскрытие Второго Принципа Платона» (The Indefinite Dyad and the Golden Section: Uncovering Plato's Second Principle), опубликованной в Международном журнале «Nexus Network Journal of Architecture and Mathematics», которая предлагается вниманию читателя.
Кто такой Скотт Олсен? Скотт Олсен является активно действующим ученым. Он работает в настоящее время Профессором Философии и Сравнительной Религии в Central Florida Community College. Получил достаточно глубокое философское образование. Степень бакалавра в области философии он получил в 1972 г. в Университете Миннесота, где написал бакалаврскую диссертацию на тему «Эстетика Платона». В 1977 г. он получил магистерскую степень в области философии в Лондонском университете, где он изучал философию Платона и Аристотеля и философию пространства-времени. В 1983 г. он защитил докторскую диссертацию на тему «Пифагореец Платон и Золотое Сечение» в области философии в Университете Флорида. В 1990 г. он избран Президентом Ассоциации философов Флориды. Проф. Олсен широко известен в научном мире своими публикациями в международных журналах на тему философии Платона, неоплатонизма, Золотого Сечения. В 2006 г. Издательство Walker Publishing, N.Y. опубликовало его книгу The Golden Section: Nature’s Greatest Secret (Золотое Сечение: важнейший секрет Природы).
Так что вряд ли Проф. Олсена можно упрекнуть в «дилетантизме» или «незнании первоисточников», потому что изучение «первоисточников» и их научный анализ и является главной темой его научных исследований.
Главный вывод исследований Олсена состоит в том, что «Золотое Сечение» является главной жемчужиной учения Пифагора и Платона.
Как же Олсен пришел к такому заключению? Для этого мы должны углубиться в философию Платона, которая не так проста для понимания, как это кажется некоторым «новым русским». Уже в самом начале своей статьи Олсен подчеркивает, что «Платон... тщательно засекретил самую глубокую Пифагорейскую доктрину в своих письменных диалогах». И далее: «Платон, прежде всего как сторонник Пифагорейских философских доктрин [2], с большой осторожностью относился ко всему, что он делал, и не раскрывал всего, находясь под присягой сохранять «тайну Учителя». Все его письма и лекции загадочны, и он только очень тщательно и тонко оставляет некоторые следы, используя которые наблюдательный читатель может раскрыть для себя некоторые глубокие доктрины. Его метод в письменных диалогах, кажется, подобен его подходу, о котором сообщают, в Академии, где он предлагал [своим ученикам] только проблему для ее решения. Он представлял проблему, загадку, аномалию, очевидное противоречие или незавершенный результат для того, чтобы внимательный студент нашел объяснительную гипотезу. Таким образом, основное намерение состояло в том, чтобы дать возможность наблюдателю (члену Академии, или читателю диалога) выдвинуть гипотезу, соответствующую решению или ответу, вместо того, чтобы принять тупиковое решение, очевидное противоречие или незавершенный результат».
В своем исследовании Скотт Олсен концентрирует внимание на некоторых важнейших идеях и принципах Платона, к которым относятся, прежде всего, Первый и Второй Принципы Платона, а также важнейшее понятие «Разделенной Линии». Без понимания этих идей очень трудно понять статью Профессора Олсена. Я не являюсь философом, как и большинство читателей моей статьи. Поэтому для ознакомления с некоторыми положениями философии Платона я предлагаю читателям обратиться к книге Джона Диллона «Наследники Платона», выставленной в русском переводе на Интернете http://www.nsu.ru/classics/plato/strom8.htm
Следуя пифагорейской традиции, Платон выдвигает два основных Принципа, которые лежат в основе Мироздания. Первый принцип он назвал «Единое», второй принцип — «Неопределенной Двоицей» (которую он обозначил термином «Большее» и «Меньшее»). «Единое» (the One) — это активный принцип, который кладет «предел» (peras) бесформенности (apeiron) противоположного принципа. «Диада» или «Неопределенная Двоица» рассматривается им как принцип двойственности, одновременно бесконечно большой или бесконечно малый. Влияние Диады в природе проявляется в протяженных величинах, избыток и недостаток в которых корректируется благодаря наложению на них правильной меры. «Неопределенная Двоица» есть по преимуществу та беспредельность или «инаковость», на которую воздействует «Единое», но, кроме того, она выступает иррациональной составляющей души, а также субстратом физического мира, «вместилищем» Тимея.
Воздействуя на «Диаду» и ограничивая ее, «Единое» порождает систему натуральных чисел, называемых «архетипическими числами», «числами-идеями» или «числами-формами». Как и пифагорейцы, особое значение Платон придает первым числам натурального ряда: один, два, три и четыре (так называемой tetraktys), которое в сумме образуют десятку (Декаду) 10=1+2+3+4. Эти первые четыре числа присутствуют в самом «Едином» и получают актуальное существование в процессе ограничения «Диады». В Метафизике Аристотель описывает этот процесс порождения первых чисел так: «Диада» порождает число два путем удвоения «Единого», а затем производит остальные числа, прибавляя к числу два и другим числам «Единое». То есть все натуральные числа порождаются в результате действия первых чисел на «Диаду» либо ее на них. Именно так, можно объяснить смысл важного места из Аристотелевой Метафизики: «Другим началом Платон считал Диаду, поскольку числа, кроме первых, порождаются из нее в результате некоего естественного процесса...».
Первые четыре числа Декады — tetraktys — играют ключевую роль в космологии Платона и его последователей. Они выступают теми принципами, которые связывают абсолютно «Единое» с трехмерным физическим миром вокруг нас. Возможно, геометрический аспект чисел проявляется только на уровне Души, ведь не случайно порождение Души в Тимее описывается в терминах четырех протяженностей и пропорций между ними (идея «Разделенной Линии» Платона). Душа проецирует эти протяженности на материю, комбинируя базовые треугольники так, чтобы сформировать четыре элемента: огонь, воздух, воду и землю. Таким образом, в Тимее строится математическая модель универсума, задавшая тон всем последующим космологическим исследованиям.
Учение о Душе — центральный, но вместе с тем и наиболее сложный элемент учения Платона. Душа есть та Мировая Душа, которая описывается в Тимее и о которой еще раз сказано в десятой книге Законов. В качестве посредника между умопостигаемым и физическим мирами Душа состоит из аспектов, которые способны отражать «высшее» и «низшее». Именно на уровне Души первые числа превращаются в точку, линию, плоскость и геометрическое тело. Согласно Аристотелю, Платон конструирует Душу из этих четырех элементов, устанавливая пропорцию между ними. Моделью Души является «Разделенная Линия», то есть линия, разделенная на четыре отрезка, каждый из которых соответствует определенному состоянию, возникающему в Душе.
После такого «введения в философию Платона» я вновь бы хотел бы возвратиться к исследованиям профессора Олсена, посвященным новому толкованию Второго Принципа Платона или «Неопределенной Двоицы», называемой также «Большим» и «Меньшим» (the Greater and the Lesser).
Олсен выдвигает весьма смелую гипотезу, касающуюся численного толкования «Большего» и «Меньшего». Он утверждает, что понятия «Большее» и «Меньшее» имеют прямое отношение к «Золотому Сечению» f, а именно:
Большее = f
Меньшее = 1 / f.
Статья Олсена и посвящена обоснованию этой гипотезы. Олсен утверждает: «Существует несколько загадок и нерешенных проблем Платона. Некоторые из них возникают в рамках диалогов, другие — в замечаниях, сделанных Аристотелем и ранними комментаторами по поводу доктрин Платона. Когда несколько из ключевых загадок рассматриваются в совокупности, они помогают указать направление требуемого решения. В частности, я утверждаю, что «Тимей» (Timaeus) и «Государство» (Republic) вместе указывают на Золотое Сечение».
В «Тимее» (Timaeus) в явном виде указание на Золотое Сечение отсутствует. Как известно, в «Тимее» Платон анализирует пять правильных многогранников, которые лежат в основе космологии Платона. При этом он описывает два элементарных треугольника, приводящих к числам Ц2 и Ц3, с помощью которых можно сконструировать четыре правильных многогранника (тетраэдр, октаэдр, куб и икосаэдр). Но в «Тимее» Платон не описывает никакого элементарного треугольника, с помощью которого можно построить Додекаэдр. Но в то же время, как подчеркивает Олсен, в «Государстве» (Republic) Платон тонко и аккуратно включает Золотое Сечение в «Разделенную Линию» (Divided Line), лежащую в основе концепции «Души» Платона. Как подчеркивает Олсен, основные сочинения Платона «Тимей» (Timaeus), «Государство» (Republic), и «Парменид» (Parmenides), рассматривают вмести, указывают на непрерывную геометрическую пропорцию (так раньше называлась Золотая Пропорция), которая лежит в основе Додекаэдра. И самое главное, Олсен доказывает, что непрерывная геометрическая пропорция или Золотое Сечение воплощены в самых важных онтологических принципах Платона, «Едином» (the One) и «Неопределенной Двоице» (Indefinite Dyad).
Олсен утверждает, что «недостающий треугольник для конструирования Додекаэдра должен быть основан на Золотом Сечении, исходя из чисто математических рассмотрений. Но почему Золотое Сечение столь сильно охраняется в рамках Пифагорейской традиции? Я хотел бы предположить здесь, что для Платона это было онтологическим приоритетом над Формами и Числами. Вложенное в него открытие является едва ли не самым главным основанием Принципа «Неопределенной Двоицы», который сам по себе является замечательным принципом».
В чем же состоит суть математического открытия Олсена, сделанного в результате исследования сочинений Платона? Он начинает с Пентаграммы, которая была хорошо известна пифагорейцам. Олсен выделяет в ней одну из линий, сохраняя ее точки пересечения.
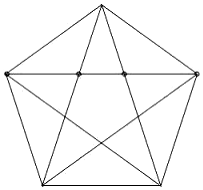
Таким образом, Олсен рассматривает отрезок ab Пентаграммы, который имеет Золотые Сечения в точках c и d.
![]()
Затем с помощью циркуля путем вращения отрезка cd (вокруг точки с), Олсен отмечает точку e на отрезке ab. При этом оказывается, что точка с, d и е являются точками «Золотого Сечения» соответственно отрезков ab, ас и cb.
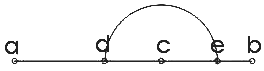
Как следует из рисунка, отрезок ab оказывается разделенным на четыре части; при этом отрезки dc и ce оказываются равными, то есть, dc = ce.
Именно этот отрезок, с точки зрения Олсена, и является моделью «Разделенной Линии», которая лежит в основе концепции «Души» Платона.
А далее Олсен рассматривает два внутренних отрезка dc и ce как отрезки, представляющие «Единицу» или «Единое». Если теперь обозначить через А – наименьший отрезок «Разделенной Линии» ab, через D – наибольший, а через С и B — внутренние отрезки, равные друг другу и равные «Единице» (С = B = 1), то оказывается, что D становится равным f, то есть «Большему», и A становится равным 1/f, то есть, «Меньшему».
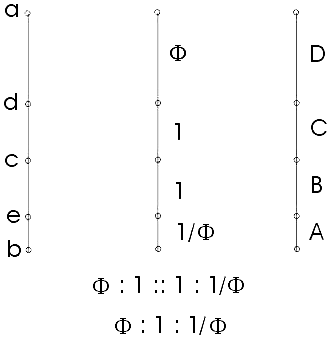
Таким образом, D : C = B : A есть ни что иное, как f : 1 = 1 : 1/f, то есть Большее: Единица = Единица: Меньшее = Золотой Пропорции. Так по Олсену выглядит «Разделенная Линия» Платона!
Главный вывод Олсена, вытекающий из этих рассуждений, состоит в том, что «Разделенная Линия» (Divided Line) объединяет Два Принципа Платона, «Единое» и «Неопределенную Двоицу», при этом они объединяются на олснове «Золотого Сечения».
Далее Олсен показывает, как с помощью «Золотого Сечения», которое лежит в основе Пентаграммы и Додекаэдра, могут быть построены элементарные треугольники, соответствующие отношениям Ц2 и Ц3, с помощью которых в «Тимее» конструируются первые четыре правильных многогранника. Построенную геометрическую фигуру он называет «Золотой Чашей Ориона». Из этих рассуждений вытекает, что «Золотое Сечение» — более элементарное, «метафизическое» знание, которое лежит в основе «Неопределенной Двоицы», «Разделенной Линии» и с помощью которого можно построить все пять Платоновых тел!
Очень интересны комментарии к статье, данные Олсеном. Отметим наиболее важные из них:
- Необходимо отметить, что есть определенное свидетельство, что Платон и его ученики работали с Золотым Сечением в Академии [Платона]. Гез (Heath) свидетельствует: «Прокл (Proclus) говорил, что Eudoxus добавил к числу теорем, которые Платон доказал, «Теорему о Сечении» и использовал в них метод анализа [abduction]. Очевидно, что «сечение» было некоторым специфическим сечением, которое во времена Платона имело большое значение; и одно «сечение», о котором это может быть так сказано, — это именно то, что называли «Золотым Сечением», а именно, делением прямой линии в крайнем и среднем отношении, которое появляется у Евклида (Книга II, Теорема. 11) и поэтому наиболее вероятно это «сечение» является «пифагорейским» [знанием]».
- Онтология Платона основана на его Пифагорейской вере, что Божественное проявляется всюду в нашем мире через Числа. Таким образом, он предлагает, чтобы Принципы Чисел, а именно, «Неопределенная Двоица» в связи с «Единым» производили или разворачивали Божественное во всех вещах с использованием числовой матрицы. Во время этого построения я попросил бы читателя вспомнить очень важный комментарий Иоганна Кеплера: «Геометрия имеет два великих сокровища: теорему Пифагора и деление отрезка в крайнем и среднем отношении (»Золотое Сечение»). Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем» [цитировано по Хэмбиджу, 1920]. Это построение воплощает в себе приложение этих «двух великих сокровищ».
Таким образом, главным результатом исследований американского философа Скотта Олсена является доказательство того факта, что «Пифагореец» Платон знал «Золотое Сечение» и воплотил его в своих главных онтологических принципах: «Едином», «Неопределенной Двоице» и «Разделенной Линии», которая лежит в основе его концепции «Душа». А поскольку Платон является последователем Пифагора, не оставившего после себя опубликованных работ, то из этого исследования вытекает, что Пифагор также знал о «Золотом Сечении», что подтверждается и многими современными исследователями (Лосевым, Эйзенштейном, Сороко, Волошиновым). И работа Скотта Олсена является блестящим примером действительно научного подхода к прочтению текстов Платона!
Текст статьи Скотта Олсена
INTRODUCTION
Plato, acting as a kind of Socratic midwife presenting problems and puzzles in much the same way to his readers as he did in the Academy, carefully secreted a most profound Pythagorean doctrine into his written dialogues. He did so for those capable of «abducting» [ 1] the solution in light of the hints he provides. Here I will attempt to uncover the nature of Plato's Second Principle, known as the Indefinite Dyad, sometimes called the Greater and the Lesser, and its relation to the Golden Section, f. The crux of my hypothesis is the following:
Greater = f
Lesser = 1 / f.
Введение
Платон, действующий как своего рода Сократова акушерка, представляющая своим читателям проблемы и загадки почти таким же способом, как он это делал в своей Академии, тщательно засекретил самую глубокую Пифагорейскую доктрину в своих письменных диалогах. Он сделал это в виде намеков, которые он приводит [в своих диалогах], для тех, кто способен к «пониманию» («abducting») [1]. Здесь я попытаюсь раскрыть природу Второго Принципа Платона, известного под названием «Неопределенная Двоица» (Indefinite Dyad), иногда называемая Большим и Меньшим, и показать его отношением к Золотому Сечению f. Суть моей гипотезы состоит в следующем:
Большее = f
Меньшее = 1 /f.
This is, to my knowledge, a novel hypothesis, and my goal in this paper is to argue its potential for validity. Recall the following facts:
![]()
![]() .
.
Given these facts and the hypothesis above, we have:
|
Greater x Lesser |
= 1 |
|
Greater — Lesser |
= 1 |
|
Greater ё Unity |
= f |
|
Unity ё Lesser |
= f |
|
Greater ё Lesser |
= f2 |
The fact that the ratio of the Greater to the Lesser is f2 and not f is crucial to my interpretation of the Indefinite Dyad. The importance of these relationships will become clear only after a review of some pertinent classical Greek philosophy. Это есть, насколько мне известно, новая гипотеза, и моя цель в этой статье состоит в том, чтобы обсудить ее обоснованность. Напомним следующие факты: Используя эти факты и высказанную выше гипотезу, мы имеем: Большее x Меньшее = 1 Большее — Меньшее = 1 Большее ё Единица = f Единица ё Меньшее = f Большее ё Меньшее = f2 Тот факт, что отношение Большего к Меньшему равно f2, в не f, является решающим в моей интерпретации Неопределенной Двоицы. Важность этих соотношений станет ясной только после обзора некоторых относящихся к теме положений греческой философии.
![]()
![]() .
.
THE PHILOSOPHICAL BACKGROUND Философское обоснование Перед тем как начать, я предлагаю следующий краткий обзор, детали которого будут обсуждены в остальной части статьи. Применение «абдуктивного» («abductive») рассуждения к загадкам Платона в диалогах приводит к решению, что Разделенная Линия (Divided Line) в «Государстве» (Republic) построена с использованием ряда Золотых Сечений (то есть, делений в крайнем и среднем отношении). Это приводит к открытию, что существует более примитивная форма, чем отношения Ц2 и Ц3 (корни, порожденные элементарным треугольникам в Тимее (Timaeus)), и что эта форма основывается на Золотом Сечении. И говоря просто, «абдуктивное» («abductive») рассуждение – это метод, с помощью которого мы приходим к решению, что число «Золотая Пропорция» и обратное к нему число – это фактически Большее и Меньшее из Неопределенной Двоицы (Indefinite Dyad) Платона.
Before starting, I offer the following overview, the details of which will be discussed in the rest of the article. An application of abductive reasoning to Plato's puzzles in the dialogues leads to the solution that the Divided Line in the Republic is constructed using a series of Golden Cuts (i.e., divisions in extreme and mean ratio). This leads to the discovery that there is a more primitive form than the Ц2 and Ц3 ratios (the roots inherent in the elementary triangles of the Timaeus), and that this form is based in the Golden Section. In fact, as we shall see, the discovery is that the Golden Section can actually be employed in the construction of these roots. And put simply, abductive reasoning is the method by which one arrives at the solution that the Golden Section and its reciprocal are in fact the Greater and the Lesser of the Indefinite Dyad.
Комментарий 1 (Стахов). «Абдуктивное» рассуждение – это вид логического рассуждения, подобного «дедуктивному» и «индуктивному» рассуждениям, широко используемым в науке. Его основное отличие от «дедуктивного» и «индуктивного» состоит в том, что оно начинается с множества фактов и дает их наиболее вероятное объяснение. Термин abduction иногда используется для обозначения множества гипотез, выдвигаемых для объяснения наблюдений и выводов.
Plato, primarily as a proponent of Pythagorean philosophical doctrines,[ 2] was very careful with what he did and did not reveal, being under an apparently severe oath of secrecy. Both his writings and lectures are enigmatic, and he only very carefully and subtly provides the clues with which the observer may be capable of uncovering the inner doctrines for themselves. His method in the written dialogues appears to be similar to his reported approach in the Academy, where he would propose the problem to be solved. He would present the problem, puzzle, anomaly, apparent contradiction or incomplete result, intending that the attentive student would abduct an explanatory hypothesis. Thus, the underlying intention was to get the observer (Academy member or dialogue reader) to abduct (hypothesize) an appropriate solution or answer, rather than to accept the dead end, apparent contradiction or incomplete result. Платон, прежде всего как сторонник Пифагорейских философских доктрин [2], с большой осторожностью относился ко всему, что он делал, и не раскрывал всего, находясь под присягой сохранять «тайну Учителя». Все его письма и лекции загадочны, и он только очень тщательно и тонко оставляет некоторые следы, используя которые наблюдательный читатель может раскрыть для себя некоторые глубокие доктрины. Его метод в письменных диалогах, кажется, подобен его подходу, о котором сообщают, в Академии, где он предлагал [своим ученикам] только проблему для ее решения. Он представлял проблему, загадку, аномалию, очевидное противоречие или незавершенный результат для того, чтобы внимательный студент нашел объяснительную гипотезу. Таким образом, основное намерение состояло в том, чтобы дать возможность наблюдателю (члену Академии, или читателю диалога) выдвинуть гипотезу, соответствующую решению или ответу, вместо того, чтобы принять тупиковое решение, очевидное противоречие или незавершенный результат.
There are several Platonic puzzles and unsolved issues. Some of these arise within the dialogues and others in remarks made by Aristotle and early commentators regarding Plato's doctrines. When several of the key puzzles are viewed in conjunction, they help point in the direction of the required solution. In particular, I will argue that the Timaeus and the Republic together point to the Golden Section. The Timaeus does so by the conspicuous absence of the Golden Section, since Plato provides no appropriate elementary triangle for the construction of the Dodecahedron, often considered the most sublime of the five solids. And in the Republic, Plato subtly and with great economy embeds the Golden Mean in the beautiful ontology of his Divided Line analogy. Together the Timaeus, Republic, and Parmenides 133b («worst difficulty argument») point to continuous geometric proportion as that which binds together Plato's realms of Being and Becoming. And finally, as we shall see, continuous geometric proportion and the Golden Mean are embedded in Plato's most important ontological principles, the One and the Indefinite Dyad. This should have special ramifications for a whole family of issues surrounding the role of geometry in aesthetics.[ 3] Существует несколько загадок и нерешенных проблем Платона. Некоторые из них возникают в рамках диалогов, другие — в замечаниях, сделанных Аристотелем и ранними комментаторами по поводу доктрин Платона. Когда несколько из ключевых загадок рассматриваются в совокупности, они помогают указать направление требуемого решения. В частности я утверждаю, что «Тимей» (Timaeus) и «Государство» (Republic) вместе указывают на Золотое Сечение. В «Тимее» (Timaeus) в явном виде Золотое Сечение отсутствует, так как Платон не описывает никакого соответствующего элементарного треугольника для построения Додекаэдра, часто рассматривая этот самый знаменитый из пяти правильных многогранников. Но в «Государстве» (Republic), Платон тонко и аккуратно включает Золотое Сечение в красивую онтологию его аналогии «Разделенной Линии» (Divided Line). Вместе «Тимей» (Timaeus), «Государство» (Republic), и «Парменид» (Parmenides 133b) («наиболее трудное сочинение ») указывают на непрерывную геометрическую пропорцию как такую, которая связывает воедино Платоновы царства Бытия и Становления. И наконец, как мы увидим, непрерывная геометрическая пропорция и Золотое Сечение воплощены в самых важных онтологических принципах Платона, «Единое» (the One) и «Неопределенной Двоице» (Indefinite Dyad). Это должно иметь специальные разветвления для целого семейства проблем, отражающих роль геометрии в эстетике [ 3].
Aristotle makes it eminently clear that within the Academy, Plato professed Two Principles, principles that were involved in the construction of the Forms (Universals or Archetypal Numbers), as well as the Sensibles (Particulars) of our Empirical World. The First Principle is generally acknowledged. It is the Good of Plato's Republic, also referred to in the Academy in its more mathematical context as the One. The other Principle was usually referred to as the Indefinite Dyad, and at times as the Greater and the Lesser, Excess and Deficiency, or the More and the Less. Occasionally one would see the Two Principles contrasted in terms of the One as Equality and the Indefinite Dyad as embodying Inequality. Аристотель предельно ясно указывает на то, что в своей Академии Платон сформулировал Два Принципа, которые вовлечены в создание «Форм» (Универсальные или Архитипичные Числа), так же, как «Рационального» (Sensibles) («Особенностей») нашего Эмпирического Мира. Первый Принцип общеизвестен. Это «Добро» (Good) «Государства» (Republic) Платона, также упоминаемый в Академии в ее более математическом контексте как «Единое» (the One). Другой Принцип обычно упоминался как «Неопределенная Двоица» (Indefinite Dyad), или иногда как Большее и Меньшее (the Greater and the Lesser), Лишнее и Недостающее (Excess and Deficiency), или Большее и Меньшее (the More and the Less). Иногда можно было бы видеть Два Принципа, противопоставленные в терминах «Единицы» (the One) как воплощение Равенства (Equality) и «Неопределенной Двоицы» (Indefinite Dyad) как воплощение Неравенства (Inequality).
Although there are important references to this Second Principle in the dialogues (especially the Philebus), there is no real clarity as to its meaning and definition. It is an understatement to suggest that Plato was reserved in his references towards it. In fact, when he apparently lectured on the subject of the One and the Indefinite Dyad in his so-called Agrapha Dogmata (Unwritten Lectures) or Lectures On the Good, he continued to veil his presentation in secrecy. Simplifies records, in his Commentarius in Physica 453.25-30:
They say that Plato maintained that the One and the Dyad were the First Principles, of Sensible Things as well. He placed the Indefinite Dyad also among the objects of thought and said it was Unlimited, and he made the Great and the Small First Principles and said they were Unlimited, in his Lectures On the Good; Aristotle, Heraclides, Hestiaeus, and other associates of Plato attended these and wrote them down in the enigmatic style in which they were delivered [Barnes 1984: 2399 (emphasis added)]. Хотя есть важные ссылки на этот Второй Принцип в диалогах (особенно Philebus), нет никакой реальной ясности относительно его значения и определения. По-видимому, будет большим преуменьшением говорить о том, что Платон был сохранен в его ссылках на этот принцип. Фактически, когда он, очевидно, читал лекции по теме «Единое» (the One) и «Неопределенная Двоица» (Indefinite Dyad) в его так называемых «Апокрифических изречениях» (Agrapha Dogmata) (Ненаписанные Лекции) или «Лекции о Добре» (Lectures On the Good), он продолжал скрывать свое представление [об этом принципе] в тайне. Простая запись в его «Комментариях к Физике» (Commentarius in Physica) гласит: Говорят, что Платон утверждал, что «Единое» и «Диада» являются Первыми Принципами, так же как и «Реальные вещи» (Sensible things). В своих «Лекциях о Добре» (Lectures On the Good) Платон поместил «Неопределенную Двоицу» (Indefinite Dyad) также среди объектов мышления и сказал, что она есть Бесконечное, и он сделал Большое и Малое Первыми Принципами и сказал, что они также являются Бесконечностью; Аристотель, Heraclides, Hestiaeus, и другие партнеры Платона посещали эти лекции и конспектировали их в том загадочном стиле, в котором они излагались [Barnes 1984: 2399].
And as these Two Principles were ontologically prior to and causally involved in the manifestation of both the Forms and Sensible things, it should not be surprising that Plato held them to be of the utmost importance. Thus we learn from Aristotle's pupil and commentator, Alexander, that these Two Principles were «more important than the Ideas» (Commentarius in Metaphysica 88.1) [Barnes 1984: 2440]. И поскольку эти Два Принципа были онтологически и причинно вовлечены в проявление как «Форм», так и «Реальных вещей» (Sensible things), не должно быть удивительным, что Платон рассматривал их, как имеющих исключительное значение. От комментатора Александра, который был учеником Аристотеля, мы узнаем что эти Два Принципа были «более важными, чем Идеи» (Commentarius в Metaphysica 88.1) [Barnes 1984: 2440].
Now according to Aristotle and others, what Plato presented to members of the Academy and in public lectures was not always identical to the content of the written dialogues. We learn from Simplicius that:
Alexander says that «according to Plato the One and the Indefinite Dyad, which he spoke of as Great and Small, are the Principles of all things and even of the Forms themselves». So Aristotle reports also in his books On the Good. One might also have got this from Speusippus and Xenocrates and the others who attended Plato's course On the Good [Simplicius on Aristotle's Physics 187a12, quoted in Kramer 1990: 203]. Сейчас, согласно Аристотелю и другим [членам Академии], мы знаем, что то, Платон излагал членам Академии в публичных лекциях, было не всегда идентично содержанию письменных диалогов. Мы узнаем из Simplicius следующее: Александр говорит, что «согласно Платону «Единое» (the One) и Неопределенная Двоица (Indefinite Dyad), о которой он говорил как о Большом и Малом (Great and Small), являются Принципами всех вещей и даже «Форм» самих по себе». Об этом Аристотель сообщает также в своих книгах о Добре. Об этом можно также узнать от Speusippus и Xenocrates и других [учениках Платона], кто посещал курс Платона «О Добре» [Simplicius on Aristotle's Physics 187a12, quoted in Kramer 1990: 203].
Thus, there is considerable evidence of Plato avowedly professing that there are the Two Principles of the One and the Indefinite Dyad.
The great mystery has always been, what exactly does Plato mean by the Indefinite Dyad, or as he called it, Excess and Deficiency, or the Greater and the Lesser. Aristotle does tell us:
Since the Forms are the causes of all other things, he thought their elements were the elements of all things. As matter, the Great and Small were Principles; as substance, the One; for from the Great and the Small, by participation in the One come the Forms, the Numbers [Metaphysics 987b19-22]. Таким образом, существует свидетельство самого Платона, прямо утверждающего, что существует Два Принципа: «Единое» (the One) и «Неопределенная Двоица» (Indefinite Dyad). Всегда было большой тайной, что же в действительности Платон понимал под «Неопределенной Двоицой» (Indefinite Dyad), или, как он называл ее, под Избытком и Недостатком (Excess and Deficiency) или Большим и Меньшим (the Greater and the Lesser). Аристотель, действительно, говорит нам: Так как «Формы» — причины всех других вещей, он думал, что их элементы были элементами всех вещей. Как материя, Большое и Малое (Great and Small) являлись Принципами; как субстанция, «Единица»; из Большого и Малого с участием «Единицы» порождаются Формы и Числа [Metaphysics 987b19-22].
And of course all Sensible objects of this world are derivative from these original Principles via the Forms or Numbers.
Now in the Timaeus, Plato boldly hints at the deeper revelations to be gained by those who carefully pursue his clues and incomplete analyses. He poses the question:
What are the most perfect bodies that can be constructed, four in number, unlike one another, but such that some can be generated out of one another by resolution? … If we can hit upon the answer to this, we have the truth concerning the generation of earth and fire and of the bodies that stand as proportionals between them [Timaeus 53e; emphasis added]. И конечно все «Реальные объекты» (Sensible objects) этого мира производны от этих оригинальных Принципов через Формы или Числа. Теперь в «Тимее» (Timaeus), Платон смело намекает на более глубокие открытия, которые будут получены теми, кто тщательно следует его рекомендациям и незавершенным исследованиям. Он ставит вопрос: Каковы самые прекрасные тела, которые могут быть построены из четырех чисел, отличные друг от друга, но такие, что некоторые могут быть произведены один из другого из друга путем разрешения? Если мы сможем найти ответ на этот вопрос, мы найдем истину, касающуюся порождения земли и огня, а также тел, которые находятся к ним в пропорциональном отношении [Timaeus 53e].
As Keith Critchlow indicates:
This demonstration of the continuing pre-eminence of proportion is followed by a curious «evasion», which we can only assume is a covering up of the fifth body [Critchlow 1994: 156; emphasis added]. Keith Critchlow свидетельствует: Эта демонстрация продолжающегося превосходства пропорции сопровождается курьезной «уловкой», которое мы можем только принять, является покрытием пятого тела [Critchlow 1994: 156]
Plato gives us the Ц2 triangle for the construction of the Cube, and the Ц3 triangle for the construction of the Tetrahedron, Octahedron and Icosahedron. But the triangle (or the root numbers embedded in it) necessary for the construction of the Dodecahedron is most conspicuously absent. Regarding the Ц2 and Ц3 primitive triangles, however, Plato states cryptically (and yet very revealingly for the astute student):
These then... we assume to be the original elements of fire and other bodies, but the principles which are prior to these Deity only knows, and he of men who is a friend of Deity.… [Anyone who can point out a more beautiful form than ours for the construction of these bodies shall carry off the palm, not as an enemy, but as a friend.... [H]e who disproves what we are saying, and shows that we are mistaken, may claim a friendly victory [Timaeus 53a-54b; emphasis added]. Платон дает нам треугольник Ц2 для конструирования Куба, и треугольник Ц3 для конструирования Тетраэдра, Октаэдра и Икосаэдра. Но треугольник (или его корень), необходимый для конструирования Додекаэдра, отсутствует, что явно бросается в глаза. Касательно примитивных треугольников Ц2 и Ц3, Платон, однако, излагает весьма загадочно (и все же очень показательно для проницательного студента): Они [эти треугольники]..., рассматриваются нами как оригинальные элементы огня и других тел, но принципы, которые лежат в их основе, известны только Богу, или тому из людей, кто является другом Бога. Любой, кто может указать более красивую форму, чем наши [треугольники] для конструирования этих тел [Платоновых тел], должен получить пальмовую ветвь не как враг, а как друг.... Тот, кто опровергает то, что мы говорим, и показывает, что мы ошибаемся, может провозгласить дружественную победу [Timaeus 53a-54b]
The missing triangle for the construction of the Dodecahedron must involve (purely from mathematical considerations) the Golden Section. But why is the Golden Section to be so protected within the Pythagorean tradition? I would like to propose here that for Plato it is its ontological priority over the Forms, the Numbers. It is the discovery that it is embedded in, if not the very basis of, the Principle of the Indefinite Dyad that is so remarkable. And as we shall see, it is this Principle along with the One that is involved in a deeper revelation regarding continuous geometric proportion. Недостающий треугольник для конструирования Додекаэдра должен быть основан на Золотом Сечении, исходя из чисто математических рассмотрений. Но почему Золотое Сечение столь сильно охраняется в рамках Пифагорейской традиции? Я хотел бы предложить здесь, что для Платона это было онтологическим приоритетом над Формами и Числами. Вложенное в него открытие является едва ли не самым главным основанием Принципа «Неопределенной Двоицы», который сам по себе является замечательным принципом. И поскольку, как мы увидим, именно этот Принцип наряду с принципом «Единого» (the One) вовлечен в более глубокое открытие, касающееся непрерывной геометрической пропорции.
In the Timaeus, Plato states:
Two things cannot be rightly put together without a third; there must be some bond of union between them. …and the fairest bond is that which makes the most complete fusion of itself and the things which it combines, and proportion (analogia) is best adapted to effect such a union. For whenever in any three numbers, whether cube or square, there is a mean, which is to the last term what the first term is to it, and again, when the mean is to the first term as the last term is to the mean — then the mean becoming first and last, and the first and last both becoming means, they will all of them of necessity come to be the same, and having become the same with one another will be all one [Timaeus 31b-32a]. В «Тимее» Платон утверждает: Две вещи не могут быть красиво соединены без третьей; должна быть некоторая связь между ними. И самая прекрасная связь есть такая, которая обеспечивает наиболее полное свое слияние с вещами, которые она объединяет, и пропорция (analogia) наилучшим способом приспособлена для того, чтобы образовать такое объединение. Поскольку всякий раз, когда в любых трех числах, кубе или квадрате существует среднее, которое так относится к первому, как первое к среднему, и снова, когда среднее так относится к первому как последнее к среднему, тогда среднее становится первым и последним, и первое и последнее становится средним. Таким образом, всё по необходимости будет тем же самым, а так как оно будет тем же самым, то оно составит целое» [Timaeus 31b-32a].
Now following the Pythagoreans, Plato places a great deal of emphasis on numbers, ratio (logos), and proportion (analogia). As Aristotle attests in several places, «…those who speak of Ideas say the Ideas are Numbers» (Metaphysics 1073a18-20). And again:
[T]he numbers are by him [Plato] expressly identified with the Forms themselves or principles, and are formed out of the Elements (i.e., Principles of the One and Indefinite Dyad). [De Anima 404b24]. Теперь вслед за Пифагорейцами Платон акцентирует свое внимание на числах, отношениях (logos), и пропорциях (analogia). Как свидетельствует Аристотель в нескольких местах, «те, кто говорит об Идеях, говорят, что Идеи есть Числа» (Metaphysics 1073a18-20). И снова: Числа им [Платоном] явно идентифицируются с Формами непосредственно или Принципами, и сформированы из Элементов (то есть, Принципами «Единое» и «Неопределенная Диада») [De Anima 404b24].
In the Republic, Plato presents a series of similes or analogies with the apparent purposes of:
- indicating a kind of ontological proportion linking together his worlds of Being and Becoming, and
- providing an epistemological framework for attaining deeper insights into the nature of reality.
В «Государстве» (Republic), Платон представляет ряд сравнений или аналогий с очевидными целями:
1. указать своего рода онтологическую пропорцию, соединяющую его миры Бытия и Становления, и
2. обеспечить эпистемологический каркас для того, чтобы достичь более глубокое понимание природу действительности.
He does this with the Sun Analogy (Republic 502d-509c), the Divided Line (509d-511e), and the Cave (514a-521b). I have discussed these metaphors elsewhere at length [Olsen 1983; 2002], and will be concerned here primarily with how the Divided Line assists in penetrating into the possible nature of the Indefinite Dyad. Он делает это с Аналогией Солнца («Республика», 502-ая-509c), Разделенной Линией (509d-511e), и Пещерой (514a-521b). Я обсудил эти метафоры в другой своей работе более подробно [Olsen 1983; 2002], и буду касаться здесь, прежде всего, того, как Разделенная Линия (Divided Line) помогает в проникновении в возможную природу «Неопределенной Двоицы» (Indefinite Dyad).
THE DIVIDED LINE AND THE «SAYRE CHALLENGE» РАЗДЕЛЕННАЯ ЛИНИЯ И «ВЫЗОВ SAYRE»
Plato begins by saying:
Suppose you have a line divided into two unequal parts, to represent the Visible and Intelligible orders, and then divide the two parts again in the same ratio (logos)… in terms of comparative clarity and obscurity [Republic 509D]. Плато начинает с высказывания: Предположим, что мы имеем линию, разделенную на две неравные части, чтобы представлять Видимые и Невидимый порядки. Разделим эти две части снова в том же самом отношении (logos) в терминах относительной ясности и мрака [Republic 509D].
Комментарий 2 (А.П. Стахов). Таким образом, Платон делит Линию на четыре части
Usually when commentators attempt to determine how the line is to be divided, they fail to first fully consider the underlying significance of Plato asking the reader to divide the line unevenly. Now it seems clear to me that if Plato is concerned primarily about continuous geometric proportion, as he appears to assert in Timaeus 31b-32a, then there is one and only one way to divide a line (and it is unevenly) such that you immediately have a continuous geometric proportion, and that is with a division in extreme and mean ratio, or what we now call a Golden Cut: [ 4]
whole line : longer segment :: longer segment : shorter segment.
Обычно, когда комментаторы пытаются определить, как линия должна быть разделена, они сразу же терпят неудачу, когда начинают рассматривать указание Платона на то, что линия разделяется на неравные части. Теперь же мне кажется ясным, что, если Платон имеет в виду прежде всего непрерывную геометрическую пропорцию, как он утверждает в «Тимее» (Timaeus) 31b-32a, тогда существует один и только один способ разделить линию на неравные части, такой, что мы немедленно получаем непрерывную геометрическую пропорцию, и это есть деление отрезка в крайнем и среднем отношении, которое мы теперь называем Золотым Сечением: вся линия так относится к большему сегменту как больший сегмент к меньшему сегменту.
Комментарий 3 (А.П. Стахов). Это – главная идея Скотта Олсена. Платон использовал «непрерывную геометрическую пропорцию» (то есть «Золотое Сечение) для деления «Разделенной Линии» на четыре части.
Plato then asks us to cut each of those two segments again in the same ratios, namely Golden Cuts. In effect what Plato is asking us to do is to perpetuate the continuous geometric proportion into the four subdivisions of his Divided Line. What he has effectively done through a series of Golden Cuts is to bind his so-called Intelligible and Sensible Worlds (and their subdivisions) together through continuous geometric proportion employing the Golden Section. Затем Платон просит нас разделить эти два сегмента снова в том же самом отношении, а именно, в Золотой Пропорции. В действительности то, что Платон просит нас сделать, это увековечивание непрерывной геометрической пропорции в виде четырех субподразделений его «Разделенной Линии» (Divided Line). Суть того, что он эффективно сделал путем использования ряда Золотых Сечений, состоит в том, что он связал свои так называемые Разумные (Intelligible) и Реальные (Sensible) Миры (и их подразделения) вместе с помощью непрерывной геометрической пропорции, основанной на Золотом Сечении.
Kenneth M. Sayre of the University of Notre Dame, in his 1983 book, posed a very interesting challenge to anyone who would propose a Golden Section solution to Plato's Divided Line. I will call it the «Sayre Challenge». He writes:
It is (barely) possible that Plato had the golden section (or golden rectangle) in mind when he constructed the Divided Line, and thought of its unique aesthetic qualities as somehow reflecting the Good as the ideal of beauty. The commentator convinced of this would have the formidable job on his hands of making sense of the extended equality,
A:B = C:D = (A+B): (C+D) = (C+D): (A+B+C+D),
which results from this interpretation [Sayre 1983: 304; emphasis added]. Kenneth M. Sayre из Университета Notre Dame в своей книге (1983), дал очень интересный вызов любому, кто предложит Золотое Сечение для «Разделенной Линии» (Divided Line) Платона. Я называю это «Вызовом Sayre». Он пишет: Вполне возможно, что Платон имел в виду Золотое Сечение (или золотой прямоугольник), когда он строил «Разделенную Линию», и думал о его уникальных эстетических качествах, отражающих так или иначе Добро как идеал красоты. Комментатор, убежденный в этом, обрекает себя на огромную работу, придавая смысл следующему расширенному равенству: A:B = C:D = (A+B): (C+D) = (C+D): (A+B+C+D), которое вытекает из этой интерпретации [Sayre 1983: 304].
I accept the challenge. In fact it will assist us in explicating the underlying significance of the Indefinite Dyad and the One. Let us take a Pentagram, which inherently contains numerous Golden Cuts, and extract one of its lines while retaining its points of intersection. Я принимаю этот вызов. Фактически это поможет нам в объяснении основного значения «Неопределенной Двоицы» (Indefinite Dyad) и «Единого» (the One). Рассмотрим Пентаграмму, которая неотъемлемо содержит многочисленные Золотые Сечения, и одну из его линий, сохраняя ее точки пересечения.
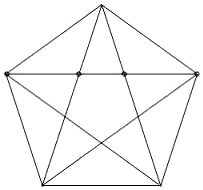
Thus, we have line ab, which has Golden Cuts at points c and d.
Таким образом, мы имеем отрезок ab, который имеет Золотые Сечения в точках c и d.
![]()
Next take a pair of compasses and, rotating line segment cd (at point с), cut line ab at point e. Далее с помощью циркуля путем вращения отрезка cd (вокруг точки с), отметим точку e на отрезке ab.
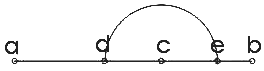
Комментарий 4 (А.П. Стахов). Заметим, что все точки d, c, e являются точками «Золотого Сечения» соответствующих отрезков: точка с делит отрезок ab в «Золотом Сечением», точки d и е – отрезки ac и cb соответственно.
One consequence of this construction is what some have referred to as the «anomaly» that line segments dc and ce must be equivalent. Sayre states:
While many commentators have noticed this anomaly, most are of the opinion that Plato either did not notice it himself or did not acknowledge it…. Whether the anomaly had any significance for Plato beyond that of an untoward mathematical consequence seems conjectural at best [Sayre 1983: 303]. Первое следствие этого построения состоит в следующем факте, который некоторые [исследователи] назвали бы «аномалией»: отрезки dc и ce должны быть эквивалентными. Sayre утверждает: В то время как многие комментаторы заметили эту аномалию, большинство считают, что Платон или не заметил эту аномалию непосредственно или не признал ее. Имела ли аномалия какое-нибудь значение для Платона, кроме этого неблагоприятного математического следствия, кажется предположительным в лучшем случае [Sayre 1983: 303].
I want to suggest that, to the contrary, the abductive solution to this so-called anomaly helps lead to the most fruitful insights. Plato knew exactly what he was doing. He was very subtly embedding the Indefinite Dyad into his Divided Line, expressing it through continuous geometric proportion. Я хочу предложить, наоборот, что «абдуктивное» (abductive) решение этой так называемой аномалии помогает прийти к наиболее плодотворным результатам. Платон знал точно, что он делал. Он очень тонко вставил «Неопределенную Двоицу» (Indefinite Dyad) в свою «Разделенную Линию» (Divided Line), выражая ее с помощью непрерывной геометрической пропорции.
I propose that the inner two line segments dc and ce should be seen as each representing Unity or One. Let us label the line in a manner consistent with the «Sayre Challenge», with A being the smallest and D the largest. Given that segments B and C are equal (each being 1), it turns out that D will be f, the Greater, and A will be 1/f, the Lesser. Я предлагаю, чтобы два внутренних линейных сегмента dc и ce рассматривались как отрезки, представляющие «Единицу» или «Единое». Будем маркировать отрезки способом, соответствующим «Вызову Sayre», то есть А – наибольший отрезок и В — наибольший. Учитывая, что отрезки B и C равны (каждый равен 1), оказывается, что оказывается, что D будет равен f, то есть Большему, и A будет равен 1/f, то есть, Меньшему.
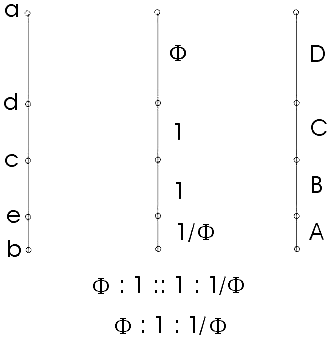
Thus, D : C :: B : A is none other than f : 1 :: 1 : 1/f, i.e., Greater: One:: One: Lesser.
Таким образом, D : C = B : A есть ни что иное, как f : 1 = 1 : 1/f, то есть Большее: Единицу = Единица: Меньшее.
In the Statesman, Plato suggests that:
It is in this way, when they preserve the standard of the mean that all their works are good and beautiful…. The greater and the less are to be measured in relation, not only to one another, but also to the establishment of the standard of the mean…. [T]his other comprises that which measures them in relation to the moderate, the fitting, the opportune, the needful, and all the other standards that are situated in the mean between the extremes [Statesman 284a1-e8; emphasis added].
В Statesman, Платон предлагает: Это именно тот путь, когда сохраняется стандарт среднего, чтобы все вещи были хороши и красивы. Большие и меньше должны быть измерены в отношении, не только друг к другу, но также и к среднему... Это другое включает то, которое измеряет их относительно среднего, соответствия подходящего и необходимого, и все другие стандарты, которые расположены в среднем между крайностями [Statesman 284a1-e8].
This agrees with my hypothesized associations. The Greater and the Lesser are to be related not only to one another, Greater: Lesser (a single proportion exhibiting the f2 ratio), but also to the standards that are situated in the mean between the extremes, Greater: One:: One: Lesser (a continued proportion exhibiting the f ratio) [ 5]. Это находится с в соответствии с моими гипотетическими ассоциациями. Большее и Меньшее должны быть связаны не только с друг другом, Большее: Меньшее равно f2, но также и к стандартам, которые расположены в среднем между крайностями, то есть, Большее: Единица = Единица: Меньшее равно непрерывной пропорции f[5].
We can now verify the «Sayre Challenge»: Мы можем теперь проверить «Вызов Sayre»:
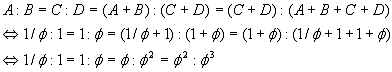
(here we have used the facts that – здесь мы использовали следующие свойства «Золотой Пропорции»: 1/f + 1 = f, 1 + f = f2, and f + f2 = f3).
The Divided Line presents Plato's Two Principles, both the One and the Indefinite Dyad. And its accomplishment is that it effectively counters the «worst difficulty» argument of Parmenides 133b, i.e., the argument that there is no connection between the Intelligible Realm (segments D and C) with the Visible Realm (segments B and A). The solution is that the two Realms are bound together through continuous geometric proportion. And not only that, but the powers of the Golden Ratio are carried into the Visible Realm as a kind of enfolded Implicate Patterned Order.[ 6] «Разделенная Линия» (Divided Line) представляет Два Принципа Платона, «Единое» и «Неопределенная Двоица». И его осуществление состоит в том, что она эффективно противостоит аргументу «худшей трудности» Parmenides 133b, то есть, аргументу о том, что нет никакой связи между Царством Разума (отрезки D, и C) с Царством Реальности (отрезки B и A). Решение состоит в том, что эти два Царства связаны с помощью непрерывной геометрической пропорции. И не только этим, но и потому что степени Золотой Пропорции переносятся в Царство Реальности как своего рода окутанный Вовлеченный Шаблонный Порядок [6].
DERIVATION OF THE ROOTS OF 2 AND 3 ВЫВОД КОРНЕЙ ИЗ ЧИСЕЛ 2 И 3
Но существует вторая часть этой истории. Следуя своему интуитивному предположению, что именно Золотое Сечение находится в центре работы Платона, и особенно после обнаружения Золотого Сечения в «Разделенной Линии» (Divided Line) (и понимая причину его отсутствия в Timaeus), я не позволил себе не бросить взгляд на некоторые дальнейшие тонкие последствия, [вытекающие из этих рассуждений]. Очень интересно, что Александр в его Комментарии Метафизики (Commentary of the Metaphysics) берет от Аристотеля этот очень многозначительный аспект теории Платона.
There is a second part to this story. While investigating my intuition that the Golden Section is at the center of Plato's work, especially after finding it in the Divided Line (and perceiving the relevance of its absence in the Timaeus), I kept an eye out for any further subtle clues. It is interesting that Alexander in his Commentary of the Metaphysics, retains from Aristotle this very telling aspect about Plato's theory:
Thinking to prove that the Equal and Unequal [other names for One and Indefinite Dyad] are first Principles of all things, both of things that exist in their own right and of opposites...he assigned equality to the monad, and inequality to excess and defect; for inequality involves two things, a great and a small, which are excessive and defective. This is why he called it an Indefinite Dyad — because neither the excessive nor the exceeded is, as such, definite. But when limited by the One the Indefinite Dyad, he says, becomes the Numerical Dyad [Barnes 1984: vol. 2, 2398; emphasis added]. Размышляя над тем, что «Равное» (Equal) и Неравное (Unequal) [другие названия для «Единого» (One) и «Неопределенной Двоицы» (Indefinite Dyad)] являются первыми Принципами всех вещей, и тех вещей, которые существуют в их собственном праве и противоположностей..., он приписал свойство равенства монаде, и свойство неравенства к избытку и недостатку; неравенство вовлекает в себя две вещи, большое и малое, которые являются чрезмерными и дефектными. Эти рассуждения объясняют, почему он назвал все это «Неопределенной Двоицей» (Indefinite Dyad) — потому что ни чрезмерное, ни превышенное таким путем является определенным. Но когда «Неопределенная Пара» (Indefinite Dyad) ограничивается «Единым» (the One), тогда, он говорит, она становится «Числовой Двоицей» (Numerical Dyad) [Barnes 1984: vol. 2, 2398].
In other words, the whole number 2 can be generated from the Indefinite dyad. Indeed, recalling that Greater — Lesser = 1, we have Greater + Unity — Lesser = 2. Другими словами, целое число 2 может быть произведено из «Неопределенной Двоицы». Действительно, если вспомнить, что Большое – Малое = 1, мы получим: Большое + Единица – Малое = 2.
Комментарий 5 (А.П. Стахов). Эти рассуждения Олсена, которые показывают, как представить число 2 через «Золотую Пропорцию» (2=f+ f-1-1), имеют чрезвычайное значение для современной теории чисел. Для этого необходимо вспомнить так называемую «систему счисления Бергмана», введенную в 1957 г. Доказано, что в этой системе любое натуральное число 1, 2, 3,... может быть представлено в виде конечной суммы степеней «Золотой Пропорции». Это означает, что «Золотая Пропорция» является «знанием», более элементарным, чем натуральные числа, так как любое натуральное число может быть представлено через «Золотую Пропорцию». Обратное неверно, то есть «Золотую Пропорцию» нельзя представить через натуральные числа. Поэтому связь этой идеи Олсена с «системой Бергмана» может быть положена в основу новой теории чисел, которая в своих началах восходит к «Неопределенной Двоице» Платона и его «Разделенной Линии».
Now the real secret of Plato's Indefinite Dyad (in addition to generating the whole numbers) is that it may be employed to derive the other crucial roots (Ц2 and Ц3) necessary for the construction of four of the five Platonic solids. А теперь секрет «Неопределенной Двоицы» Платона (в дополнение к генерации целых чисел) состоит в том, что его можно использовать, чтобы вывести другие важные корни (Ц2 and Ц3), необходимые для конструирования четырех из пяти Платоновых тел.
The following construction is the result of carefully combining two insights, one that I had regarding Ц3, and one that Mark Reynolds shared with me regarding Ц2. While contemplating the nature of the Indefinite Dyad, which I had already decided must be the Golden Section and its reciprocal, I had a dream in which I saw the Greater and the Lesser as the legs of a right-angled triangle of which the hypotenuse was Ц3. I jumped out of bed and grabbed a pair of compasses, straightedge and pencil. I did the construction and lo and behold it was true (as we'll verify mathematically below). Следующее построение — результат осторожного объединения двух идей, одна из них касается Ц3, и вторая касается Ц2 (эту идею я узнал от Mark Reynolds). Рассматривая природу «Неопределенной Двоицы» (Indefinite Dyad), которую по моему мнению должна быть Золотой Пропорцией и обратным ей числом, я мечтал увидеть «Большее» и «Меньшее» (the Greater and the Lesser) как бедра прямоугольного треугольника, гипотенуза которого была бы равна Ц3. Я выпрыгнул из кровати и захватил пару циркулей, прямоугольник и карандаш. Я сделал построение и вдруг увидел, что оно было верным (как мы проверим математически ниже).
Then a year later I had the good fortune of meeting Mark Reynolds. I shared this construction with him, and he in turn showed me how Ц2 was derivable, in a very similar manner, from the Lesser and the square root of the Greater as legs of a right-angled triangle.[ 7] (In both cases I was attending the KAIROS Summer School studying under Dr. Keith Critchlow and John Michell — Buckfast Abbey in Devon, England in 1997, and Crestone, Colorado in 1998.) Год спустя мне повезло встретить Mark Reynolds. Я рассказал ему о моих геометрических построениях, и он, в свою очередь, показал мне, как можно получить корень Ц2 подобным способом, от «Меньшего» (the Lesser) и квадратного корня Большего (the Greater) как катетов прямоугольного треугольника [7]. (В обоих случаях я посещал Летнюю Школу KAIROS, которая функционировала под руководством Доктора Keith Critchlow и John Michell — Аббатство Buckfast в Девоне, Англия, 1997, и Crestone, Колорадо, 1998.)
The construction of the Indefinite Dyad Template follows. Though the construction has already proven to harbor many wonderful properties, notice in particular the Quadrilateral DKMH, which acts as a kind of ontological entheogenomatrix.[ 8] Because of its morphology and seemingly sublime function, I propose to name it the «Golden Chalice of Orion». Построение Шаблона «Неопределенного Двоицы» (Indefinite Dyad) состоит в следующем. Хотя построение, как уже доказано, скрывает много замечательных свойств, в частности, Четырехугольник DKMH, который действует как своего рода онтологическая геноматрица [8]. В силу его морфологии и по-видимому возвышенной функции, я предлагаю назвать его «Золотой Чашей Ориона» («Golden Chalice of Orion»).
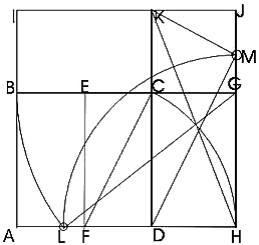
- Construct Square ABCD with side AB = 1 (построим квадрат ABCD со стороной 1).
- Construct the Golden Rectangle ABGH from Square ABCD using diagonal FC (построим Золотой Прямоугольник ABGH из квадрата ABCD, используя диагональ FC).
- Construct Square AIJH by extending line AB to I, and line HG to J (in both cases extend the line lengths by the equivalent of DH or 1/f), and connect I to J Построим квадрат AIJH путем расширения отрезка AB до I и отрезка HG до J (в обоих случаях увеличиваем длины отрезков на длину отрезка DH или 1/f) и соединим I с J.
- AH = AI = IJ = HJ = f.
- Extend line DC intersecting line IJ at K. Расширим отрезок DC до пересечения с отрезком IJ в точке K.
- DK = f.
- DH = KJ = CK = 1/f.
- Cut line AH at L by rotating side GB (at point G). Using the Pythagorean Theorem on right triangle GHL, since GL = f, GH = 1, and 1 + f = f2, we obtain HL = Цf. Пересечем отрезок AH в точке L путем вращения стороны GB (с центром в точке G). Применяя Теорему Пифагора к прямоугольному треугольнику GHL (GL = f, GH = 1, and 1 + f = f2), мы получаем HL = Цf.
- Cut line HJ at M by rotating line HL (at point H); HM = Цf. Пересечем отрезок HJ в точке M путем вращения отрезка HL (с центром в точке H); HM = Цf.
- Using the Pythagorean Theorem, DH2 +
HM2 = DM2; thus we have,
Применяя Теорему Пифагора, DH2 + HM2 = DM2; тогда мы имеем
(1/f)2 + (Цf)2
= DM2
1/f2 + f
= DM2
(1 — 1/f) + (1/f + 1)
= DM2
2
= DM2
- So that DM = Ц2 (here we have used the facts that 1/f2 + 1/f=1, and 1/f +1=f).[ 9] Так что DM = Ц2 (здесь мы используем следующие свойства Золотой Пропорции: 1/f2 + 1/f=1, и 1/f +1=f)
- Using the Pythagorean Theorem, DH2 +
DK2 = KH2; thus we have,
Используя Теорему Пифагора DH2 +
DK2 = KH2, тогда мы
имеем
(1/f)2 + (f)2= KH2
1/f2 + f2
= KH2
(1 — 1/f) + (1 + f)
= KH2
(1 — 1/f) + (1 + 1/f + 1)
= KH2
3
= KH2
- So that KH = Ц3 (here we have used the facts that 1/f2 + 1/f=1, and 1/f +1=f, and 1 + f = f2). Так что KH = Ц3 (здесь мы использовали следующие свойства Золотой Пропорции: 1/f2 + 1/f=1, 1/f +1=f, 1 + f = f2)
(For completeness, we note that KM » 0.708, which is within 0.2% of Ц2/2.) The amazing fact is that the two diagonals of the «Golden Chalice of Orion» are precisely Ц2 and Ц3! Для завершенности мы замечаем, что KM »0.708, которое с точностью до 0.2% совпадает с Ц2/2. Удивительный факт состоит в том, что две диагонали «Золотой Чаши Ориона» в точности равны Ц2 и Ц3!
Hence, Ц2 and Ц3 are ultimately derivable from the Greater (DK = f) and the Lesser (DH = 1/f).[ 10] As a result, the Indefinite Dyad gives rise to the roots that are employed in the construction of the Cube, Tetrahedron, Octahedron and Icosahedron. And of course this Second Principle is directly related to the derivation of the Dodecahedron. As such, the One and Indefinite Dyad were for the Pythagorean Plato the Principles behind all of existence. In the end, I suspect that this was the great Pythagorean secret that Plato could not openly reveal, but only hint at, expecting his attentive followers to abduct the solution. We begin to see why Plato was so careful not to reveal the real nature of the Golden Section and its reciprocal, respectively the Greater and the Lesser. Таким образом,, Ц2 и Ц3 непосредственно выводятся из «Большого» (DK = f) и «Меньшего» (DH = 1/f) [ 10]. В результате «Неопределенная Двоица» дает начало корням, которые используются при построении Куба, Тетраэдра, Октаэдра и Икосаэдра. И конечно, этот Второй Принцип непосредственно связан с построением Додекаэдра. Так же, «Единое» (the One) и «Неопределенная Двоица» (Indefinite Dyad) были для Пифагорейца Платона основными Принципы всего сущего. В заключение, я подозреваю, что это было большой Пифагорейской тайной, о которой Платон не мог открыто рассказать, но мог только намекнуть, ожидая, что его внимательные последователи найдут это решение. Мы начинаем понимать, почему Платон так боялся раскрыть истинную природу Золотой Пропорции и обратного к ней числа, соответственно «Большего» и «Меньшего» (the Greater and the Lesser).
NOTES (ЗАМЕЧАНИЯ)
Этот метод вывода был описан одним из его больших его приверженцев, философом / математиком Charles Sanders Peirce, как «абдукция», «ретродукция» или новое рассуждение. Peirce утверждал, что он новь открыл «абдуктивное» (abductive) рассуждение в работах Платона и Аристотеля. В Академии, проблемы, которые требовали «абдуктивных» (abductive) решений, включали, например, геометрические задачи, касающиеся Золотого Сечения, удвоения куба, «сведения» одной проблемы к другой, и попытке «спасти приличия» при объяснении очевидного нерегулярного движения планет. Последнее привело к великолепному возникновению гипотезы Евдокса (Eudoxus) о концентрических сферах. Что касается «абдуктивного» (abductive) рассуждения самого по себе, см. [Olsen 1983: 8-44; Olsen 2002: 85-99].
[1] This method of inference has been variously described by one of its great exponents, the philosopher/ mathematician Charles Sanders Peirce, as abduction, retroduction, or novel reasoning. Peirce maintained that he rediscovered the abductive reasoning process in the works of Plato and Aristotle. In the Academy, problems that required abductive solutions included, for example, geometric problems regarding the Golden Section, the Delian Problem of doubling the cube, «reduction» of one problem to another, and the attempt to «save the appearances» of the apparent irregular motion of the planets. The last resulted in a magnificent abduction by Eudoxus of his explanatory hypothesis of concentric spheres. As for the abductive reasoning process itself, see [Olsen 1983: 8-44; Olsen 2002: 85-99]. return to text
[2] I have argued this point exhaustively elsewhere, and would at this stage simply refer the reader to my dissertation [Olsen 1983], especially pp. 45-121. return to text Я обсудил эту проблему исчерпывающе в другом месте, и на данном этапе просто отнес бы читателя к моей диссертации [Olsen 1983], особенно pp. 45-121].
[3] It should be noted that there is definite evidence that Plato and his pupils were working with the Golden Section in the Academy. Heath relates, «We are told by Proclus that Eudoxus 'greatly added to the number of the theorems which Plato originated regarding the section, and employed in them the method of analysis [abduction].' It is obvious that the section was some particular section which by the time of Plato had assumed great importance; and the one section of which this can safely be said is that which was called the 'golden section,' namely the division of a straight line in extreme and mean ratio which appears in Eucl. II. 11 and is therefore most probably Pythagorean»[1956: v. 1, 137]. return to text Необходимо отметить, что есть определенное свидетельство, что Платон и его ученики работали с Золотым Сечением в Академии [Платона]. Гез (Heath) свидетельствует: «Прокл (Proclus) говорил, что Eudoxus добавил к числу теорем, которые Платон доказал, «Теорему о Сечении» и использовал в них метод анализа [abduction]. Очевидно, что «сечение» было некоторым специфическим сечением, которое во времена Платона имело большое значение; и одно «сечение», о котором это может быть так сказано, — это именно то, что называли «Золотым Сечением», а именно, делением прямой линии в крайнем и среднем отношении, которое появляется у Евклида (Книга II, Теорема. 11) и поэтому наиболее вероятно это «сечение» является «пифагорейским» [знанием]» [1956: v. 1, 137].
[4] Others have proposed the principle of the golden section in the Divided Line (see [Brumbaugh 1954] and [Des Jardins 1976]) or a Fibonacci approximation to it [Dreher 1990]. But these prior attempts do not embody the essential features of the Greater and Lesser (Indefinite Dyad) in relation to the One, as I depict them below. For a critique of the sufficiency of earlier arguments (taken individually) that attempt to establish the golden sectioning of the Divided Line, see [Balashov 1994]. return to text Другие ученые предложили принцип золотого сечения в Разделенной Линии (см. [Brumbaugh 1954] и [Des Jardins 1976]), или «фибоначчиеву» аппроксимация к нему [Dreher 1990]. Но эти предшествующие попытки не воплощают существенные свойства «Большего» и «Меньшего» («Неопределенной Двоицы») в отношении к «Единому», как я изображаю их ниже. Для критического анализа достаточности более ранних аргументов (взятых индивидуально), которые пытаются установить золотое сечение Разделенной Линии, см. [Balashov 1994].
[5] We could also simply begin with the line as Unity, and then do the subsequent cuts. The initial golden cut of the line would then give us a longer and a shorter segment, namely, 1/ fand 1/f2, and hence, (1/f): (1/f2) would be in fratio. I suspect that the understandable mistake of earlier commentators who were close to uncovering Plato's mystery, and hence the failure to notice the actual relationship between the Greater and the Lesser, follows from the tendency to associate Plato's Greater of the Indefinite Dyad with the «greater» of the two line segments, and the Lesser of the Indefinite Dyad with the «lesser» of the two line segments. With my interpretation, when we divide the line in this way, Unity becomes the «Greater», 1/ fbecomes the «Mean», and 1/f2becomes the «Lesser», relatively speaking. If again, we proceed further with this initial golden cut of a line of Unity, and do our subsequent two golden cuts, we discover that the four resulting line segments are in the following continued proportion: (1/f2): (1/f3):: 1/f3: 1/f4. Here, relatively speaking, 1/f2«acts» as the Greater, 1/f3«acts» as the Mean, and 1/f4«acts» as the Lesser. The relation here of the Greater to the Mean, and the Mean to the Lesser, is again the fratio. And 1/f2(the Greater) in relation to 1/f4(the Lesser in this context) is f2. The advantage of portraying the divisions of the line as I do in this paper, is simply to more clearly reveal the underlying essence of the ratios, as they reflect the One and the Indefinite Dyad, i.e., Greater: 1:: 1: Lesser. Otherwise there is a tendency to overlook the crucial f2relationship between the Greater and Lesser that lies at the heart of this paper. return to text Мы могли также просто начать с единичного отрезка, и затем сделать его последующие сечения. Начальное золотое сечение единичного отрезка дало бы нам больший и меньший отрезки, 1/ fи 1/f2, и следовательно, отношение (1/f): (1/f2) было бы равно «Золотой Пропорции». Я подозреваю, что понятная ошибка более ранних комментаторов, которые были близко к раскрытию тайны Платона, и следовательно неудача попытки заметить фактические отношения между «Большим» и «Меньшим» вытекает из тенденции ассоциировать «Большее» Платона из «Неопределенной Двоицы» с «большим» из этих двух отрезков, и «Меньшее» из «Неопределенной Двоицы» с «меньшим» из этих двух отрезков. В моей интерпретации, когда мы делим отрезок таким образом, чтобы «Единица» становилась «Большим», то 1/fстановится «Средним», а 1/f2становится «Меньшим», собственно говоря. Если снова, мы переходим далее с этому начальному золотому сечению «Единицы», и делаем наши последующие два золотых сечения, мы обнаруживаем, что четыре получающихся линейных сегмента находятся в следующей непрерывной пропорции: (1/f2): (1/f3) = 1/f3: 1/f4. Здесь, собственно говоря, 1/f2«действует» как «Большее», 1/f3 «действует» как «Среднее», и 1/f4«действует» как «Меньшее». Здесь отношение «Большего» к «Среднему», и «Среднего» к «Меньшему» снова равно «Золотой Пропорции».. И 1/f2(«Большее») к 1/f4(«Меньшему» в этом контексте) равно f2. Преимущество описания «Разделений Линии», которое я делаю в этой статье, просто более ясно показывает основную сущность отношений, так как они отражают «Единое» и «Неопределенную Двоицу», то есть, «Большее»: 1 = 1: «Меньшее». Другими словами, существует тенденция пересмотреть критическое отношение f2 между «Большим» и «Меньшим», которое и лежит в основе этой статьи.
[6] Here I am thinking of the Implicate Order that David Bohm, the physicist, suggested is enfolded into the outer Explicate Order of our world. This «patterned order» enfolded into Nature appears to be closely related to the continuous geometric proportion of the One and Indefinite Dyad as expressed, for example, in Fibonacci and Lucas whole number approximations in minerals, plants, animals, microtubules and DNA. See, for example, [Bohm 1980; Dixon 1992; Goodwin 1994; Penrose 1994; Martineau 1995]. return to text Здесь я думаю о «Вовлеченном Порядке» (Implicate Order), предложенный физиком David Bohm, окутан во внешний Объяснимый Порядок (Explicate Order) нашего мира. Этот «стандартный порядок», проявляющийся в Природе, кажется тесно связанным с непрерывной геометрической пропорцией «Единого» и «Неопределенной Двоицы», что выражается в, например, в проявлениях чисел Фибоначчи и Люка в минералах, растениях, животных, микроканалах и ДНК. См., например [Bohm 1980; Dixon 1992; Goodwin 1994; Penrose 1994; Martineau 1995
[7] Neither Mark nor I labor under any false illusion that we have discovered these things; we have simply rediscovered them independently. Perhaps we are uncovering what for many in the past may have been restricted or esoteric knowledge. return to text Ни Марк, ни я не заблуждались ложной иллюзией, что мы обнаружили эти вещи; мы просто открыли вновь их независимо. Возможно, мы раскрываем то, что для многих в прошлом, возможно, было засекречено или тайное знание
[8] Plato's ontology is based upon his Pythagorean belief that the Divine manifests throughout our world through the Numbers. Thus, he appears to be suggesting that the Principles of the Numbers, namely the Indefinite Dyad in relation to the One, generate or unfold the Divine within all things through this number matrix. During this construction, I would ask the reader to keep in mind a very important comment by Johannes Kepler: «Geometry has two great treasures: one is the theorem of Pythagoras; the other the division of a line into extreme and mean ratio [golden cut]. The first we may compare to a measure of gold; the second we may name a precious jewel» [quoted in Hambidge 1920]. This construction in effect embodies the application of these «two great treasures». return to text Онтология Платона основана на его Пифагорейской вере что Божественное проявляется всюду в нашем мире через Числа. Таким образом, он предлагает, чтобы Принципы Чисел, а именно, «Неопределенная Двоица» в связи с «Единым» производили или разворачивали Божественное во всех вещах с использованием числовой матрицы. Во время этого построения я попросил бы читателя вспомнить очень важный комментарий Иоганна Кеплера: «Геометрия имеет два великих сокровища: теорему Пифагора и деление отрезка в крайнем и среднем отношении (»Золотое Сечение»). Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем» [цитировано по Хэмбиджу, 1920]. Это построение воплощает в себе приложение этих «двух великих сокровищ».
[9] This is Mark Reynolds's very important contribution that allows this «Platonic Template» to work. return to text Это — очень важный вклад Mark Reynolds, который позволяет сконструировать этот «Платонический Шаблон»
[10] Notice also the relationship between the sides of the three squares, AI: AB: CK. They are in the continuous geometric proportion, f: 1: 1/f. Thus they perpetuate the frelationship. In the case of the areas of the three squares, we have the f2relationship perpetuated throughout. Square AIHJ: Square ABCD: Square CKJG = f2: 1: 1/f2. return to text Отметим также следующее соотношение между сторонами этих трех квадратов: AI: AB: CK. Они связаны непрерывной геометрической пропорцией: f: 1: 1/f. Таким образом, они увековечивают отношение «Золотой Пропорции». Для случая площадей этих трех квадратов мы имеем отношение f2, увековеченное здесь. Квадрат AIHJ: квадрат ABCD: квадрат CKJG = f2: 1: 1/f2.
REFERENCES
Balashov, Yuri. 1994. Should Plato's Line be Divided in the Mean and Extreme Ratio? Ancient Philosophy 14: 283-295.
Barnes, Jonathan, ed. 1984. The Complete Works of Aristotle, vol. 2. Princeton: Princeton University Press.
Bohm, David. 1980. Wholeness and the Implicate Order. London: Routledge & Kegan Paul.
Brumbaugh, Robert. 1954. Plato's Mathematical Imagination. Bloomington: Indiana University Press.
Cairns, Huntington and Edith Hamilton, eds. 1971. The Collected Dialogues of Plato. Princeton: Princeton University Press.
Condat, Jean-Bernard, ed. 1988. The Golden Section and Music. Frankfurt: Verlag Peter Lang.
Critchlow, Keith. 1963. Order in Space. New York: Thames and Hudson.
Critchlow, Keith. 1994. The Platonic Tradition on the Nature of Proportion. Pp. 133-168 in Homage to Pythagoras, C. Bamford, ed. New York: Lindisfarne Press.
Des Jardins, G. 1976. How to Divide the Divided Line. Review of Metaphysics 29: 483-496.
Dixon, Robert. 1992. Green Spirals. Pp. 353-368 in Spiral Symmetry, I. Hargittai & C.A. Pickover, eds. River Edge, NJ: World Scientific.
Dreher, John Paul. 1990. The Driving Ratio in Plato's Divided Line. Ancient Philosophy 10: 159-172.
Dunlap, Richard A. 1997. The Golden Ratio and Fibonacci Numbers. River Edge, NJ: World Scientific.
Fideler, David. 1993. Jesus Christ, Sun of God. Wheaton, Illinois: Quest Books.
Goodwin, Brian. 1994. How the Leopard Changed Its Spots. New York: Simon & Schuster.
Hackforth, R., trans. 1972. Plato's Phaedo. Cambridge: Cambridge University Press.
Hambidge, Jay. 1920. The Elements of Dynamic Symmetry: the Greek Vase. New Haven: Yale University Press.
Heath, Thomas L. 1956. The Thirteen Books of Euclid's Elements. 3 vols. 2nd ed. 1926. Rpt. New York: Dover Publications.
Herz-Fischler, Roger. 1987. A Mathematical History of the Golden Number. New York: Dover Publications.
Kirk, G.S. and R.E. Raven. 1975. The Presocratic Philosophers. Cambridge: Cambridge University Press.
Koshy, Thomas. 2001. Fibonacci and Lucas Numbers with Applications. New York: John Wiley & Sons.
Kramer, H.J. 1990. Plato and the Foundations of Metaphysics. J.R. Caton, ed. and trans. New York: State University of New York Press.
Kuhn, Thomas. 1970. The Structure of Scientific Revolutions. Chicago: Chicago University Press.
Martineau, John. 1995. A Book of Coincidence. Powys, Wales: Wooden Books.
Michell, John. 1988. The Dimensions of Paradise. London: Thames and Hudson.
Glenn R. Morrow. trans. 1992. Proclus: A Commentary on the First Book of Euclid's Elements. Princeton: Princeton University Press.
Mueller, Ian. 1992. Mathematical method and philosophical truth. Pp. 170-199 in The Cambridge Companion to Plato. Richard Kraut, ed. Cambridge: Cambridge University Press.
Olsen, Scott A. 1983. The Pythagorean Plato and the Golden Section: a Study in Abductive Inference. Ph.D. Dissertation, University of Florida.
Olsen, Scott A. 2002. Plato, Proclus and Peirce: Abduction and the Foundations of the Logic of Discovery. Pp. 85-99 in Neoplatonism and Contemporary Thought, Part One. R. Baine Harris, ed. New York: State University of New York Press.
Pacioli, Luca. 1982. De Divina Proportione. Milano: Silvana Editoriale.
Peirce, Charles S. 1931-1958. Collected Papers of Charles Sanders Peirce, 8 vols. A.W. Burks, C. Hartshorne, and P. Weiss, eds. Cambridge: Harvard University Press.
Penrose, Roger. 1994. Shadows of the Mind. Oxford: Oxford University Press.
Sayre, Kenneth M. 1983. Plato's Late Ontology: A Riddle Resolved. Princeton: Princeton University Press.
Schwaller de Lubicz, R.A. 1998. The Temple of Man. Deborah Lawlor and Robert Lawlor, trans. Rochester, Vermont: Inner Traditions.
Stewart, Ian. 1998. Life's Other Secret. New York: John Wiley & Sons.
Taylor, A.E. 1926. Forms and Numbers: A Study in Platonic Metaphysics (I). Mind 36: 12-33.
Taylor, A.E. 1928. A Commentary on Plato's Timaeus. Oxford: Oxford University Press.
Taylor, Thomas. 1804. The Works of Plato, 5 vols. London: R. Wilks.
Taylor, Thomas. 1983. The Theoretic Arithmetic of the Pythagoreans. York Beach, Maine: Samuel Weiser.
Thomas, Ivor. ed. 1957. Greek Mathematical Works, vol. 2. Cambridge: Harvard University Press.
Thompson, D'Arcy Wentworth. 1928. Excess and Defect: Or the Little More and the Little Less.
Mind 38: 43-55.
Thompson, D'Arcy Wentworth. 1992. On Growth and Form. New York: Dover Publications.
Scott A. Olsen, Неопределенная Двоица и Золотое Сечение: Раскрытие Второго Принципа Платона. (Перевод, Предисловие и комментарии А.П. Стахова) // «Академия Тринитаризма», М.,
|
|