|
|
|
А.С. Харитонов
Классические дифференциальные уравнения имеют статистический смысл и являются верными только для средних значений большого числа отдельных элементарных процессов. К этим элементарным процессам обычно относят квантовые закономерности, автор же предполагает, что к элементарным процессам также относятся структурные изменения в сложных системах. Предлагается структурное описание сложных систем, при котором классические уравнения равновесия получают статистический смысл и являются верными только для средних значений, возникающих в результате взаимодействия структурных изменений.
Усредненное описание связано всегда с потерей информации об элементарных процессах, и характер потери информации зависит от способа и масштаба усреднения. Поэтому классические дифференциальные уравнения справедливы для описания консервативных систем, когда набор структурных состояний зафиксирован, и эволюцией можно пренебречь. Число реализованных структур в объекте всегда намного меньше числа возможных и между ними идет постоянная борьба за существование. Под структурой можно понимать связь трех и более последовательностей событий.
Примером неприменимости классических дифференциальных уравнений могут служить фракталы и сложные системы. Под сложными системами будем понимать такие системы, для описания которых термодинамический предел не применим, у которых нет основного классического равновесного состояния. К таким сложным системам можно отнести макромолекулу в термостате, стекло и плазму, а также биологические и социально-экономические системы/1/. Особенностью этих систем является спонтанное изменение структуры динамических элементов при постоянстве внешних условий. Система, состоящая из элементов с фиксированной структурой элементов, может выйти из состояния равновесия или прямолинейного равномерного движения только под действием внешних сил, система с переменной структурой элементов может создавать внутренние движущие силы и за счет них обладает самодвижением и эволюцией.
Если в качестве элементов системы принять «трубочки», которые в результате воздействие шума ветра могут резонировать усиливать одни гармонии ветра и подавлять другие гармонии, как это предложил Н. А.Умов в 1902 году /2/, то к такой системе возможно развитие за счет структурных резонансов и качество энергии может частично повышаться. Но тогда мы должны отказаться от постулата «система состоит из одинаковых элементов» и разработать описание систем, обусловленных взаимодействием структурных процессов. Взаимодействие структур, способных через механизмы «резонанса» рекуррентно порождать новые структуры, должна описываться на основе других исходных постулатов.
Ниже рассмотрим попытку объединить известное описание структурных закономерностей с законами равновесной статистики.
Простейшие структурные изменения описываются, как известно, правилом «золотой пропорции», краткое содержание которого приведем ниже.
«Золотая пропорция» возникает при весьма общих предположениях: аддитивности-
А=В+С,
и рекуррентности: каждый элемент есть сумма двух предыдущих:
| А(n)= A(n-1)+A(n-2) | (1) |
Каждая структура в природе по уравнению (1) возникает с учетом существования других предшествующих структур.
Не трудно убедится, что при А(1) ≥0 и A(2) >0 рекуррентное уравнение (1) приближает при n>10 отношение А(n)/ A(n+1) к «золотой пропорции» ф =0,618…:
и к ее квадрату
A(n)/A(n+2) ![]() ф2.
ф2.
ф2 =, 0381….
Из этого следует, что структурная организация природы связана в пределе с правилом «золотой пропорции» представления целого в виде суммы двух неравных частей:
| (2) |
Если построить график отношения А(n)/ A(n+1) от n, то можно увидеть как возникают затухающие колебания около «золотой пропорции» по уравнению (1).
Обратим внимание на то, при итерации — умножении самой на себя «золотая пропорция» порождает ряды Фибоначчи и Люка и себя самую, а также множественные свои разветвления.
Используем итерацию умножения большей величины в данном случае ф на выражение (2). На первом шаге получим:
![]() .
.
Повторим эту операцию умножения для большей величины ф2, и получим:
![]() .
.
Повторим операцию умножения большей величины на единицу, представленную разложением по «золотой пропорции», получим:
Далее при повторении имеем:
![]() .
.
В пределе получаем разбиение единицы на две части по формуле:
| (3) |
где Fn ряд Фибоначчи имеет вид:
0, 1, 1, 2, 3, 5,8,13,21,34,55,89,144,…
и возникает естественным образом из этой итерации «золотой пропорции».
Ряд Люка имеет вид:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199,....
Он равен сумме двух рядов Фибоначчи, сдвинутых на два шага:
Ln-1= Fn+F(n-2)
для n>2.
Для больших n из выражений (7) следует для чисел ряда Люка
приближенное соотношение:
![]() .
.
Традиционно «золотую пропорцию» определяют из предела отношения последующих членов ряда Фибоначчи:
или членов ряда Люка:
Если бы в системах существовал только процесс разбития большего на меньшие части по рассмотренной итерации, то мы наблюдали бы численное предельные по формуле (3):
Эти численные выражение мало известны, что указывает на то, что в природе имеет место не только процесс разбиения большего на меньшие части по рассмотренной итерации. Поэтому рассмотрим процесс итерации умножения выражения (2) самого на себя.
В этом случае разбиение системы на части описывается биномом Ньютона:
| (4) |
где 0Ј nЈ mЈ Ґ; С – число сочетаний из m элементов по n.
Целое разбивается на равновесные структурные части в пределе по формуле (4). Формула (4) описывает не только разбиения целого на части, но и объединение одинаковых частей в новые большие части по закону биномиальных коэффициентов ![]() . Возникает не пара частей как по уравнению (3), а их совокупность (n+1) элементов при m=const.
. Возникает не пара частей как по уравнению (3), а их совокупность (n+1) элементов при m=const.
Члены ряда Фибоначчи Fn являются скрытыми и непроявленными закономерностями в формуле (4) и описываются по формуле/ 3/:
Кроме того, в формуле (4) скрыто множество возникновений «золотой
пропорции», если пользоваться простейшим численным значением «золотой пропорции»:
Это возникновение ф можно предположить в результате «взаимодействие» двух и трех последовательных чисел ряда Фибоначчи и ряда Люка. Они образуют заново «золотые пропорции» ф**, что можно предположить из их свойств. Ряд Фибоначчи порождает следующие числовые закономерности:
и
Ряд Люка порождает его дополнение до удвоенной «золотой пропорции».
![]() ,
,
и
Таким образом, из приведенных примеров итерации можно видеть, что «золотая пропорция» порождает ряды Фибоначчи и Люка, а также порождает через них саму себя многими способами. Через каждые пять- шесть шагов итерации по n возможно самоорганизации локального равновесия по ф –возникновение группы с внутренними интересами (своей свободой воли). Целое порождает относительно независимые части, обладающие свойствами целого, то есть ему подробные. Другими словами, при n>5 нарушается детерминизм организации системы, а подобие сохраняется.
Итак, благодаря итерации исходная система уравнений (1) порождает саму себя ф, которая обладает цикличностью, самовоспроизведением, размножением и разветвленной сетью:
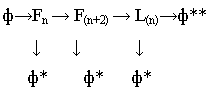 |
(5) |
Где числа ряда Люка и Фибоначчи воспроизводят «золотую пропорцию» разными способами как предел рекуррентного ряда ф* и как истинное ее значение ф**. Если не было бы специфического «взаимодействия» членов ряда Люка и Фибоначчи, то «золотая пропорция» ф* была редким событием в системе, а за счет их «взаимодействия» ф** должна быть в природе очень частым явлением. Что подтверждает практика, описанная, например, в сборнике работ /3/. От каждого равновесия по «золотой пропорции» можно выстраивать за счет итерации в цикле заново рассмотренную схему (5). Это свойство позволяет нам говорить об алгебраических фрактальных свойствах «золотой пропорции». Где под фракталом понимается объект, имеющий разветвленную структуру. Части фрактала подобны всему объекту.
При усреднении «золотой пропорции»
формула (4) вырождается в биномиальное распределение
где 0Ј nЈ mЈ Ґ; С – число сочетаний из m элементов по n.
Из этого примера можно видеть колоссальную потерю информации о структурных свойствах систем при их усредненном описании.
Выше полученный результат физически можно трактовать так. В природе идут процессы не только рассеяния «энергии» — разбиения большего на меньшие части, но происходят процессы концентрации ее в виде порождения больших новых структурных единиц бытия.
Возникает естественный вопрос, откуда может взяться итерация событий в естественной природе, да еще по «золотой пропорции»? Для ответа на этот вопрос воспользуется предыдущими работами /1,5,6/.
Ранее для учета процессов рассеяния и концентрации энергии автор предложил использовать новое определение энтропии, как суммы мер хаоса и порядка:
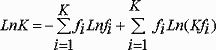 = I+ G, = I+ G, |
(6) |
где LnK – безразмерная энтропия, I – мера неопределенности состояния, а G — мера определенности состояния системы, новая функция для описания природы. На основе исследования /1,5,6/ уравнение (6) получено целесообразность введения третьего пространства событий – l набора типов степеней свободы, характеризующего рекуррентное изменение структуры элементов.
Далее уравнение (6) было преобразовано к виду:
| (7) |
где I-мера неопределенности поведения системы, мера хаоса, G-мера определенности поведения системы, мера порядка, fi(p,q,l) -вероятность трех классов переменных.
На основе уравнения (7) предположена модель равновесия сложных систем в виде равенства мер хаоса и порядка, определенных на трех классах переменных:
| I(p,q,l…) = G(p,q,l…) | (8) |
Всякое отклонение от исходного состояния будет описываться рекуррентной зависимостью, приводящей к «золотой пропорции».
| D I(p)+D I(q)+D I(l)=0. | (9) |
Насколько возрастает мера хаоса по одним переменным, настолько же она уменьшается по другим переменным. При этом изменения организации системы затрагивают три класса переменных и удовлетворяют количественно методу Фибоначчи и в пределе правилу «золотой пропорции». При этом мера хаоса или порядка удовлетворяют требований аксиоматики теории вероятности и могут рассматриваться как значение вероятности при новом итерационном рассмотрении системы.
Согласно этому способу описания в природе имеют место три универсальных процесса: рост порядка G, рост хаоса I и стремление к их равновесию за счет постоянного изменения структуры элементов l.
Усредняя свойства системы в соответствии с эргодической гипотезой, в рамках которой справедлива современная статистическая физика, мы теряем информацию о структурном многообразии и симметрии хаоса и порядка по «золотой пропорции», и получаем законы статистической механики и термодинамики с их парадоксами и противоречиями опыту эволюции систем.
Преимущество структурного способа описания систем состоит в том, что он впервые содержит не только процессе деградации, но процесс развития, когда увеличение структурной энтропии компенсирует уменьшение термодинамической энтропии:
D I(l)= -D I(p) — D I(q)
Важно, что статистическая сумма для трех классов зависимых переменных уже не задает единственного равновесного состояния, она многозначна и неустойчива, но за то имеет наглядную простую проверку с помощью чисел Фибоначчи или правила «золотой пропорции». Это выражение открывает возможность разработки новой технологии анализа равновесности сложных систем.
Выражение для свободной энергии с учетом трех классов переменных приобрело следующий вид:
Fmin = E- kT {S(p)+S(q)+S(l)}max.
Для пояснения новизны этой формулы приведем ее выражение, принятое в термодинамике:
Fmin = U- kT S(p,q)max,
где E=2U.
Вместо максимального значения энтропии как функции двух независимых классов переменных (p,q) нами введен новый принцип максимума суммы трех энтропии, так что три класса переменных оказываются взаимно зависимыми.
Эта зависимость позволяет исследовать структурные свойства природы, связанные с перераспределением энергии внутри системы между тремя классами переменных (тремя сущности природы). При внешнем равновесии системы по постулату (8) имеем новые процессы, описываемые уравнением:
∆S(p)+∆S(q)+∆S(l)=0
где ∆S(p)- приращение энтропии по импульсам, ∆S(q) — приращение энтропии по координатам, ∆S(l) — приращение энтропии по структурному многообразию частиц.
Постоянное изменение структуры динамических элементов ∆S(l)>0 может приводить к итерации — умножению «золотой пропорции» саму на себя, которую мы использовали в начале статьи. Постоянная итерация событий — повторение рекуррентных процессов поддерживает равновесие мер хаоса и порядка, определенных на трех классах переменных. Постоянные изменения по одним и тем же правилам приводят к определенному закону организации системы и к росту ее структурного многообразия. Структурная энтропия постоянно растет от любой наперед выбранной точки отсчета. При этом интегральные структуры могут поддерживать себя за счет изменения структур низшего ранга. Таким образом, итерация, которую можно делать на компьютере, идет в природе естественным путем.
Как представляется автору, преимущество структурного описания природы за счет итерации «золотой пропорции» состоит в том, что выполняются законы сохранения, превращения и взаимосвязи плюс новый закон борьбы структур за существование, ответственный за итерацию процессов в природе. В результате такого описания сохраняется цельность системы, раскрывается ее самодвижение, рост многообразия, цикличность и разветвление. Открывается новый принцип познания:
Часть может быть подобна целому в своем равновесии по «золотой пропорции».
Сделаем еще одно предположение из этой работы. Пусть каноническое распределение энергии, описываемое с помощью экспоненты, совпадает для больших n с биномом Ньютона для «золотой пропорции». Обе формулы являются формулами полного набора вероятностей и могут быть между собой согласованными.
| (10) |
Тогда парадокс равновероятности может быть разрешен следующим способом. Парадокс равновероятности состоит в том что: при еi –const все события равновероятны — постулат Больцмана или постулат Гиббса о микроканоническом распределении. Как писал сам Л.Больцман в своих лекциях, если события были бы равновероятными в изолированной равновесной системе, то в природе не было бы никакого движения.
Из уравнения (10) можно видеть, что каждому микроканоническому распределению с энергией еi или равновероятному событию можно поставить в соответствие произведение двух распределений по «золотой пропорции», умноженных биномиальный коэффициент за счет расширения пространства событий до трех классов переменных:
Отсюда следует, что равновероятное (эргодическое) пространство событий классической статистики разворачивается в пространство событий, устроенное по «золотой пропорции», где идет борьба структур за существование. Рекуррентные последовательности событий выстраиваются по «золотой пропорции» — объекты стремятся к равновесию. Стремление к равновесию идет в конфигурационном, импульсном и структурном пространствах микросостояний. Все стремится к тройственному гармоническому равновесию, но разными способами. Между этими способами достижения гармонического равновесия идет постоянная борьба структур за существование, поэтому это структурное равновесие асимптотически неустойчиво.
ТАБЛИЦА СРАВНЕНИЯ
ТЕРМОДИНАМИЧЕСКОГО И СТРУКТУРНОГО ОПИСАНИЯ
ОБЩИЕ ПОЛОЖЕНИЯ
|
где ei — энергия на степень свободы, kT-температура системы |
РАЗЛИЧИЯ ЭТИХ СПОСОБОВ ОПИСАНИЯ
|
Существование термодинамического предела N/V=const при V→∞ предполагает фиксированный набор структурных состояний. |
Существование равновесия мер хаоса и порядка, определенных в трех классах переменных, предполагает постоянную борьбу структур за существование. |
|
Системы стремятся к термодинамическому равновесию. |
Сложные системы стремятся к гармоническому равновесию трех сущностей. |
|
Термодинамическое равновесие — устойчиво |
Гармоническое равновесие –неустойчиво |
|
Угрозой жизни является «тепловая смерть Вселенной» |
Угрозой жизни является структурная неустойчивость природы. |
|
Внутренняя энергия равна сумме свободной и связанной (тепловой) энергии: U(p,q) =F+Q |
Полная энергия пропорциональна сумме мер хаоса и порядка, определенных в трех классах переменных: E(p,q,l)= kT(I +G) |
|
Энтропия равна мере хаоса: S=- S fLnf= LnW(p,q)=I(p,q) (p,q)- независимые два класса переменных |
Энтропия равна сумме мер хаоса и порядка: S=- S fLnf + S fLn(Kf)= I+G=LnK(p,q,l) и состоит из трех частей: распределения элементов в пространстве q, распределения по скоростям р и распределения по структуре элементов l: S= {S(q) +S(p)+S(l)} |
|
Свободная энергия равна: F min = U- kT S(p,q)max |
Свободная энергия равна: F min = E- kT{S(p)+S(q)+S(l)}max |
|
«Жизнь есть устойчивое неравновесие». |
«Жизнь есть неустойчивое равновесие». |
|
«Жизнь питается отрицательной энтропией» ∆S(p,q)<0 |
«Жизнь борется за структурную энтропию» ∆S(l)>0 |
|
Распределение Больцмана частиц по объему Распределение Максвелла частиц по скоростям Распределение структур исключено постулатом об одинаковости частиц. |
Распределение Больцмана частиц по объему Распределение Максвелла частиц по скоростям Распределение структур в пределе стремится к «золотой пропорции». |
- Харитонов А.С«.Поиск закономерностей устойчивого развития сложных систем», Прикладная физика, №6, 2000, с.113-119.
- Умов Н.А.. Физико-математическая модель живого. М., 1902 г.
- Реньи А. Трилогия о математике. М., Мир. 1980. С. 375.
- Владимиров Ю.С. Сб. Метафизика ХХ1 века. М. Бином. 2006.
- Харитонов А.С. «Симметрия мер хаоса и порядка в системах с постоянно изменяющейся структурой динамических элементов», Физика, Известия вузов, №1, 2004, с. 46-51.
- Харитонов А.С. « Симметрия хаоса и порядка в круговороте энергии (Холистическая парадигма природы, человека и общества)».- М.: Издательско-аналитический центр «Энергия».2004. С.172.
А.С. Харитонов, Структурное описание сложных систем // «Академия Тринитаризма», М.,
|
|
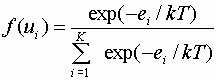 ,
,