И последнее. Для теории «Золотого Сечения» и его приложений не имеет никакого значения – знал ли Пифагор, Платон или Евклид о «Золотом Сечении». Золотое Сечение существует объективно и независимо от мнения Белянина и его «друзей». «Теория Золотого Сечения» является активно развивающейся отраслью современной науки, которая уже существенно повлияла на развитие современной науки и содержит в себе много глубоких идей, которые могут привести к новым научным открытиям.

Текст статьи J. J. O'Connor и E. F. Robertson

Euclid, in The Elements, says that the line AB is divided in extreme and mean ratio by C if AB:AC = AC:CB.

Евклид в своих Началах говорит, что отрезок АВ делится в крайнем и среднем отношении, если AB:AC = AC:CB (Рис.1).

Рис. 1. Деление отрезка в крайнем и среднем отношении («Золотое Сечение»)

Although Euclid does not use the term, we shall call this the golden ratio. The definition appears in Book VI but there is a construction given in Book II, Theorem 11, concerning areas which is solved by dividing a line in the golden ratio. As well as constructions to divide a line in the golden ratio, Euclid gives applications such as the construction of a regular pentagon, an icosahedron and a dodecahedron. Here is how the golden ratio comes into the construction of a pentagon.

Хотя Евклид и не использовал этот термин, мы будем называть его Золотым Сечением или Золотой Пропорцией. Это определение дается в Книге VI, но существует геометрическое построение, данное в Книге II, Теорема 11, касающееся площадей. Это построение осуществляется путем деления отрезка в Золотом Сечении. В качестве примеров таких построений Евклид приводит пентагон, икосаэдр и додекаэдр. В настоящей статье мы показываем, как Золотое Сечение используется при построении пентагона.

First construct an isosceles triangle whose base angles are double the vertex angle. This is done by taking a line AB and marking C on the line in the golden ratio. Then draw a circle with centre A radius AB. Mark D on the circle so that AC = CD = BD. The triangle ABD has the property that its base angles are double its vertex angle.

Сначала сконструируем «золотой» равнобедренный треугольник, в котором углы при основании равны удвоенному углу при вершине. Для этого возьмем отрезок AB и найдем точку C, которая делит отрезок в Золотом Сечении. После этого проведем дугу радиусом AB с центром в точке А. Найдем на дуге такую точку D, чтобы AC = CD = BD. Тогда треугольник ABD будет обладать таким свойством, что его углы при основании BD будут равны удвоенному значению угла при вершине А.

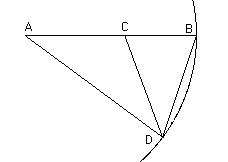
Рис.2. Геометрическое построение «золотого» равнобедренного треугольника

Now starting with such a triangle ABD draw a circle through A, B and D. Then bisect the angle ADB with the line DE meeting the circle at E. Note that the line passes through C, the point dividing AB in the golden ratio. Similarly construct F and draw the pentagon AEBDF.

Затем, начиная с треугольника ABD, проведем окружность через точки A, B и D (Рис.3). Тогда биссектриса угла ADB пресекается с этой окружностью в точке Е. Заметим, что биссектриса DE проходит через точку С, которая делит отрезок AB в Золотом Сечении. Аналогично можно построить точку F, после чего можно нарисовать пентагон (Рис.2)

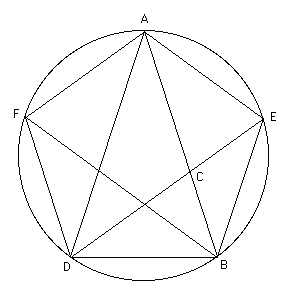
Рис.3. Геометрическое построение пентагона

Of course nobody believes that Euclid's Elements represents original work so there is the question of who studied the golden ratio before Euclid. Now some historians believe that Book II of The Elements covers material originally studied by Theodorus of Cyrene while others attribute the material to Pythagoras, or at least to the Pythagoreans. Proclus, writing in the fifth century AD, claims:-

Eudoxus... multiplied the number of propositions concerning the section which had their origin in Plato, employing the method of analysis for their solution.

Естественно, никто не верит, что Начала Евклида представляют собой оригинальное сочинение. Поэтому возникает вопрос: кто изучал Золотое Сечение до Евклида? Сейчас некоторые историки утверждают, что Книга II Начал содержит материал, впервые изучавшийся Теодором из Кирены (Theodorus of Cyrene), в то время как другие историки приписывают этот материал Пифагору или, по крайней мере, пифагорейцам. Прокл (Proclus) (5-е столетие н.э.) утверждает:

«Евдокс (Eudoxus)... приумножил число пропорций (касающихся сечения), которое берут свое начало у Платона, применившего аналитический метод для их решения»

Many believe that by 'section' Proclus means 'golden ratio'. Eudoxus certainly attended lectures by Plato so it is entirely reasonable that he might work on topics suggested during these lectures. Heath writes in his edition of Euclid's Elements:-

This idea that Plato began the study of [the golden ratio] as a subject in itself is not in the least inconsistent with the supposition that the problem of Euclid II, 11 was solved by the Pythagoreans.

Многие утверждают, что под «сечением» в этой цитате Прокл (Proclus) понимает «Золотое Сечение». Евдокс (Eudoxus) определенно посещал лекции Платона, так что вполне возможно, что он мог разрабатывать темы лекций Платона. Гез (Heath), автор книги «A history of Greek mathematics» (1921), пишет в своих редакционных замечаниях к Началам Евклида:

«Идея о том, что Платон начал изучать «Золотое Сечение», как объект сам по себе, нисколько не противоречит гипотезе, что проблема Евклида II, 11 была решена пифагорейцами»

Heath claims later in the same work that the construction of a pentagon using the isosceles triangle method referred to above was known to the Pythagoreans so there is a fair amount of evidence to suggest that this is where the study of the golden ratio began.

Гез (Heath) утверждает в некоторых работах, что построение пентагона на основе метода «золотого» равнобедренного треугольника, описанного выше, было известно пифагорейцам, так что существует достаточно много убедительных доказательств, что именно пифагорейцы первыми начали изучать «Золотое Сечение».

Hypsicles, around 150 BC, wrote on regular polyhedra. He is the author of what has been called Book XIV of Euclid's Elements, a work which deals with inscribing regular solids in a sphere. The golden ratio enters into the constructions.

Гипсикл (Hypsicles) (около 150 г. до н.э) писал о правильных многогранниках. Он является автором книги, которая была названа Книгой XIV Начал Евклида, сочинения, которое имело дело с вписыванием правильных многогранников в сферу. В этих построениях широко используется «Золотое Сечение».

Up to this time the golden ratio seems to have been considered as a geometrical property and there is no obvious sign that any attempt was made to associate a number with the ratio. Of course if AB has length 1 and AC = x where C divides AB in the golden ratio, then we can use simple algebra to find x.

1/x = x/(1 — x) gives x² + x — 1 = 0 so x = (√5-1)/2.

Then the golden ratio is 1/x = (√5 + 1)/2 = 1.6180339887498948482...

Вплоть до настоящего времени «Золотое Сечение» рассматривалось как геометрическое свойство и далеко не очевидным является ассоциация числа с «золотым Сечением». Естественно, что если AB имеет единичную длину и AC = x, где С делит AB в «Золотой Пропорции», тогда мы можем использовать очень простую алгебру для нахождения x.

1/x = x/(1 — x) gives x² + x — 1 = 0 so x = (√5-1)/2.

Тогда «Золотое Сечение» есть: 1/x = (√5 + 1)/2 = 1.6180339887498948482...

Heron certainly begins to compute approximate ratios, and in his work he gives approximate values for the ratio of the area of the pentagon to the area of the square of one side. With Ptolemy trigonometric tables, at least in terms of chords of circles, begin to be computed. He calculates the side of a regular pentagon in terms of the radius of the circumscribed circle.

Герон (Heron) определенно начал вычислить приближенные отношения, и в своей работе он дает приближенное значение для отношения площади пентагона к площади квадрата единичной длины. Он использовал для своих вычислений тригонометрические таблицы Птоломея (Ptolemy) и дуги окружностей. Он вычисляет сторону регулярного пентагона в терминах радиуса описанной окружности.

With the development of algebra by the Arabs one might expect to find the quadratic equation (or a related one) to that which we have given above. Al-Khwarizmi does indeed give several problems on dividing a line of length 10 into two parts and one of these does find a quadratic equation for the length of the smaller part of the line of length 10 divided in the golden ratio. There is no mention of the golden ratio, however, and it is unclear whether al-Khwarizmi is thinking of this particular problem.

С развитием алгебры, начало которой созданы арабами, можно было ожидать найти рассмотренное выше квадратное уравнение. Аль-Хорезми (Al-Khwarizmi), в самом деле, сформулировал много проблем по делению отрезка длиной 10 на две части и одна из них привела к квадратному уравнению для длины меньшей части отрезка длины 10, разделенного в «Золотой Пропорции». Здесь нет упоминания о «Золотом Сечении», однако, неясно, думал ли Аль-Хорезми (Al-Khwarizmi) об этой специфической задаче.

Abu Kamil gives similar equations which arise from dividing a line of length 10 in various ways. Two of these ways are related to the golden ratio but again it is unclear whether Abu Kamil is aware of this. However, when Fibonacci produced Liber Abaci he used many Arabic sources and one of them was the problems of Abu Kamil. Fibonacci clearly indicates that he is aware of the connection between Abu Kamil's two problems and the golden ratio. In Liber Abaci he gives the lengths of the segments of a line of length 10 divided in the golden ratio as √125 -5 and 15 — √125.

Абу Камиль (Abu Kamil) дает подобные уравнения, которые возникают из деления отрезка длины 10 различными способами. Два из этих способов имеют отношение к «Золотому Сечению», но снова неясно: знал ли Абу Камиль (Abu Kamil) «Золотое Сечение».

Pacioli wrote Divina proportione (Divine proportion) which is his name for the golden ratio. The book contains little new on the topic, collecting results from Euclid and other sources on the golden ratio. He states (without any attempt at a proof or a reference) that the golden ratio cannot be rational. He also states the result given in Liber Abaci on the lengths of the segments of a line of length 10 divided in the golden ratio. There is little new in Pacioli's book which merely restates (usually without proof) results which had been published by other authors. Of course the title is interesting and Pacioli writes:

... it seems to me that the proper title for this treatise must be Divine Proportion. This is because there are very many similar attributes which I find in our proportion — all befitting God himself — which is the subject of our very useful discourse.

Пачоли (Pacioli) написал Divina proportione (Божественная пропорция) – так он назвал «Золотое Сечение». Книга содержит мало нового по этой теме и включает результаты, изложенные в Началах Евклида и других источниках по «Золотому Сечению». Пачоли утверждает (без какого-либо доказательства), что «Золотое Сечение» не может быть рациональным числом. Он также излагает результат, изложенный в Liber Abaci, о длинах отрезков отрезка длины 10, разделенного в «Золотой Пропорции». В книге Пачоли мало новых результатов. В книге излагаются результаты, полученные другими авторами. Конечно, название книги оригинальное. Пачоли пишет:

«... мне кажется, что подходящее название для этого трактата должно быть Божественная Пропорция. Это потому, что есть очень много подобных признаков, которые я нахожу в нашей пропорции, которые соответствуют непосредственно самому Богу, который является предметом нашей очень полезной беседы».

He gives five such attributes, perhaps the most interesting being:-

... just like God cannot be properly defined, nor can be understood through words, likewise this proportion of ours cannot ever be designated through intelligible numbers, nor can it be expressed through any rational quantity, but always remains occult and secret, and is called irrational by the mathematicians.

Он дал много таких свойств, возможно, наиболее интересным из них является следующее:

«...подобно тому, как Бог не может быть ни определен, ни словом разъяснен, наша пропорция не может быть выражена ни доступным нам числом, ни какой бы то ни было рациональной величиной и остается скрытой и тайной и поэтому математиками названа иррациональной».

Cardan, Bombelli and others included problems in their texts on finding the golden ratio using quadratic equations. A surprising piece of information is contained in a copy of the 1509 edition of Pacioli's Euclid's Elements. Someone has written a note which clearly shows that they knew that the ratio of adjacent terms in the Fibonacci sequence tend to the golden number. Handwriting experts date the note as early 16^th century so there is the intriguing question as to who wrote it. See [6] for further details.

Кардан (Cardan), Бомбелли (Bombelli) и другие математики включали в своих сочинениях задачи по нахождению «Золотого Сечения», используя квадратные уравнения. Удивительная информация содержится в копии Начал Евклида 1509 г. издания, принадлежащей Пачоли. Кто — то написал в ней примечание, из которого ясно следует, что в тот период было известно, что отношение соседних чисел Фибоначчи стремится к «Золотой Пропорции». Анализ почерка эксперта показывает, что примечание относится к началу 16-го столетия. Поэтому возникает интригующий вопрос относительно того, кто же является автором этого примечания. См. [6] для дальнейших деталей.

The first known calculation of the golden ratio as a decimal was given in a letter written in 1597 by Michael Maestlin, at the University of Tьbingen, to his former student Kepler. He gives «about 0.6180340» for the length of the longer segment of a line of length 1 divided in the golden ratio. The correct value is 0.61803398874989484821.... The mystical feeling for the golden ratio was of course attractive to Kepler, as was its relation to the regular solids. His writings on the topic are a mixture of good mathematics and magic. He, like the annotator of Pacioli's Euclid, knows that the ratio of adjacent terms of the Fibonacci sequence tends to the golden ratio and he states this explicitly in a letter he wrote in 1609.

Первое известное вычисление значения «Золотой Пропорции» в десятичной системе счисления было дано в письме, написанном в 1597 Михаилом Маэстлином (Michael Maestlin) (Тюбингенский университет) к своему первому студенту Кеплеру. Он дал значение «около 0.6180340» для длины большего сегмента единичного отрезка, разделенного в «Золотой Пропорции». Более точное значение равно: 0.61803398874989484821.... Для Кеплера характерно мистическое отношение к золотому сечению в связи с тем, что «Золотое Сечение» имеет непосредственную связь с правильными многогранниками. Письма Кеплера на эту тему представляют собой смесь хорошей математики и магии. Он, как и комментатор Пачиолиного «Евклида», знал, что отношение соседних чисел Фибоначчи стремится к «Золотой Пропорции». Эта информация изложена Кеплером в письме, написанном в 1609.

The result that the quotients of adjacent terms of the Fibonacci sequence tend to the golden ratio is usually attributed to Simson who gave the result in 1753. We have just seen that he was not the first give the result and indeed Albert Girard also discovered it independently of Kepler. It appears in a publication of 1634 which appeared two years after Albert Girard's death.

Математический результат, свидетельствующий о том, что отношение соседних чисел Фибоначчи в пределе стремится к «Золотой Пропорции», обычно приписывают Симсону (Simson), который получил этот результат в 1753 г. Однако мы только что увидели, что он не был первым, кто получил этот результат. Действительно, Альберт Джирард (Albert Girard) также открыл этот результат независимо от Кеплера. Этот результат изложен в публикации от 1634, которая появилась спустя два года после смерти Альберта Джирарда (Albert Girard).

In this article we have used the term golden ratio but this term was never used by any of the mathematicians who we have noted above contributed to its development. We commented that «section» was possibly used by Proclus although some historians dispute that his reference to section means the golden ratio. The common term used by early writers was simply «division in extreme and mean ratio». Pacioli certainly introduced the term «divine proportion» and some later writers such as Ramus and Clavius adopted this term. Clavius also used the term «proportionally divided» and similar expressions appear in the works of other mathematicians. The term «continuous proportion» was also used.

В этой статье мы используем термин «Золотое Сечение», однако этот термин никогда не использовался кем-либо из математиков, внесших существенный вклад в его развитие. Мы упоминали выше, что, возможно, термин «сечение» впервые использовался Проклом (Proclus), хотя некоторые историки утверждают, что термин «сечение» и означает «Золотое Сечение». Общий термин для обозначения этого понятия, использовавшийся ранними исследователями, был просто «деление в крайнем и среднем отношении». Пачоли определенно ввел термин «Божественная пропорция» и некоторые поздние авторы, такие как Рамус (Ramus) и Клавиус (Clavius) использовали этот термин. Клавиус (Clavius) также использовал термин «пропорционально разделенный» («proportionally divided») и подобные же выражения возникали в работах других математиков. Использовался также термин «непрерывная пропорция» («continuous proportion»).

The names now used are golden ratio, golden number or golden section. These terms are modern in the sense that they were introduced later than any of the work which we have discussed above. The first known use of the term appears in a footnote in Die reine Elementar-Matematik by Martin Ohm (the brother of Georg Simon Ohm):-

One is also in the habit of calling this division of an arbitrary line in two such parts the golden section; one sometimes also says in this case: the line r is divided in continuous proportion.

Названия, которые используются сейчас: «золотая пропорция» (golden ratio), «золотое число» (golden number) или «золотое сечение» (golden section). Эти термины являются современными в том смысле, что они были введены позже тех работ, которые мы обсуждали выше. Первое известное использование этого термина возникает в сносках книги Die reine Elementar-Matematik Мартина Ома (Martin Ohm), брата Георга Ома (Georg Simon Ohm):

«Существует также привычка называть это деление произвольного отрезка на две такие части «Золотым Сечением»; иногда также говорят в этом случае: отрезок r разделен в непрерывной пропорции».

The first edition of Martin Ohm's book appeared in 1826. The footnote just quoted does not appear and the text uses the term «continuous proportion». Clearly sometime between 1826 and 1835 the term «golden section» began to be used but its origin is a puzzle. It is fairly clear from Ohm's footnote that the term «golden section» is not due to him. Fowler, in [9], examines the evidence and reaches the conclusion that 1835 marks the first appearance of the term.

Первое издание книги Мартина Ома (Martin Ohm) относится к 1826 г. Вышеупомянутая сноска в тексте не появляется, и в тексте используется термин «непрерывная пропорция». Ясно где-то между 1826 и 1835 термин «Золотое Сечение » начал использоваться, но его происхождение является загадкой.

The golden ratio has been famed throughout history for its aesthetic properties and it is claimed that the architecture of Ancient Greece was strongly influenced by its use. The article [11] discusses whether the golden section is a universal natural phenomenon, to what extent it has been used by architects and painters, and whether there is a relationship with aesthetics.

Золотая пропорция стала знаменитой в истории из-за ее эстетических свойств. Утверждается, что архитектура Древней Греции была полностью под влиянием «Золотой Пропорции». В статье [11] обсуждается, является ли «Золотое Сечение» универсальной пропорцией Природы, в какой степени она использовалось архитекторами и живописцами, и имеет ли она отношение к эстетике.

Литература

Книги:

1. R Herz-Fischler, A mathematical history of division in extreme and mean ratio (Waterloo, Ontario, 1987).
2. R Herz-Fischler, A mathematical history of the golden number (New York, 1998).

Статьи:

3. E Ackermann, The golden section, Amer. Math. Monthly 2 (1895), 260-264.
4. R Archibald, The golden section — Fibonacci series, Amer. Math. Monthly 25 (1918), 232-237.
5. F Campan, The golden section (Romanian), Revista Stiintifica «V. Adamachi» 33 (1947). 225-231.
6. L Curchin and R Herz-Fischler, De quand date le premier rapprochement entre la suite de Fibonacci et la division en extrкme et moyenne raison?, Centaurus 28 (2) (1985), 129-138.
7. R Fischler, On applications of the golden ratio in the visual arts, Leonardo 14 (1981), 31-32; 262-264; 349-351.
8. R Fischler, How to find the golden number without really trying, Fibonacci Quart. 19 (1981), 406-410.
9. D H Fowler, A generalization of the golden section, Fibonacci Quart. 20 (2) (1982), 146-158.
10. J Kappraff, The relationship between mathematics and mysticism of the golden mean through history, in Fivefold symmetry (River Edge, NJ, 1992), 33-65.
11. J Mawhin, Au carrefour des mathйmatiques, de la nature, de l'art et de l'йsotйrisme: le nombre d'or, Rev. Questions Sci. 169 (2-3) (1998), 145-178.
12. G Sarton, When did the term golden section or its equivalent in other languages originate, Isis 42 (1951), 47.
13. A P Stakhov, The golden section in the measurement theory, in Symmetry 2: unifying human understanding, Part 2, Comput. Math. Appl. 17 (4-6) (1989), 613-638.
14. A J van Zanten, The golden ratio in the arts of painting, building and mathematics, Nieuw Arch. Wisk. (4) 17 (2) (1999), 229-245.

.