Институт Золотого Сечения -Дискуссии

Сергей А. Алферов

Так получилось, что второй раз я вошел в Сад Золотой пропорции как раз через «модуль качания». «Модуль качания» – это пара прямоугольных треугольников, стоящих на едином катете, таких, что гипотенуза одного равна катету другого. Когда их представляешь схемой с единым катетом в основании и другими катетами по бокам, то получается, что катет-гипотенуза «качается» на одной точке.

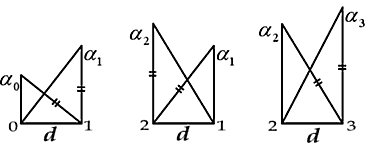
Качаясь то на одном, то на другом конце общего катета, модуль возрастает вверх до бесконечности, образуя некую «линию углов»; или уходит вниз, но до определенного «начала», до угла «a ₀» конкретной «линии качания». Модуль качания по его смыслу оказался модулем определенной пирамиды… И эта тропа повела дальше очень далеко.

Мы здесь остановимся, приведя формулы углов некоторых «линий качания» и уйдем по тропе спиралей. Вот формулы углов 3-х самых знаменитых «линий качания», последовательно уменьшающихся от «a ₀» с возрастанием «i». Движение их еще пригодится нам…

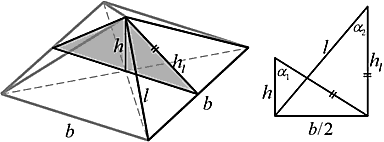
Когда рисовалась первая последовательность «качающихся треугольников», так вышло, что исходный модуль (с углами «a ₀-a ₁») оказался самым удивительным из всех возможных модулей. Пересеченные его гипотенузы образуют ортогональные оси, по которым развивается «Золотая спираль». Этот модуль образует пирамиду «Золотой спирали». Пирамида Хеопса с множеством найденных к настоящему времени замечательных соотношений своей геометрии – это и есть пирамида «Золотой спирали»… Но вернемся снова к теме сегодняшней (и постараемся больше не отвлекаться).

Итак, перед нами лежит модуль с углами «В₀-В₁», тангенсы которых равны соответственно Ц j ₂ и Ц j ₁. Это – начало спирали. Проводя от пиков модуля горизонтальные (или вертикальные) отрезки до пересечения с ее осями, мы получаем основу спирали. Смотрите.

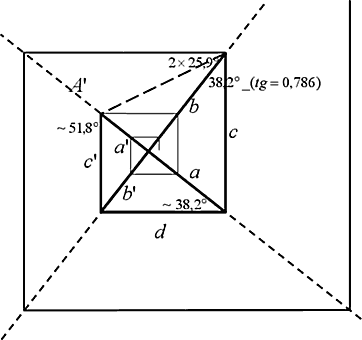
На схеме постоянно возникают эти углы, и на отрезках образуются золотые пропорции. a’ + a = c и a: c = 0,618, тогда a’: a = 0,618.

И точно также b’: b = 0,618. Или можно так доказать золотое сечение в нашей спирали: a: a’ = (a:b’)(b’:a’) = 0,786х0,786 = 0,618 Примечательно — c’ = a и d = b.

А «c»..., чему оно равняется дальше по порядку?... Посмотрите на чертёж. Она равняется следующему значению «А’» на оси «А» от центра до очередного угла.

И этот порядок, раскручиваясь, уходит дальше в бесконечность. Это спираль с коэффициентом изменения отрезков от перпендикуляра к перпендикуляру k=Ц 0,618 = 0,786 при "скручивании" и k=Ц 1,618 = 1,272 при раскручивании.

Увеличить >>>

И при этом всегда сторона собственно спирали (гипотенуза) равна отрезку оси на следующем по возрастанию шаге. Как она красиво, гармонично развивается! Мало того, отрезок, соединяющий вершины наших треугольников (a ₀ и a ₁), делит угол отходящего витка спирали к оси, равный тем же 51,8°, ровно пополам (2х25,9°).

Ничего такого нет ни в одной другой спирали. Она по праву может называться "золотой спиралью"; а не j -спираль, коэффициент которой равен 1,618/0,618, которая просто отрабатывает угол j и у которой как и у всех остальных спиралей d № b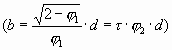

Ладно, пусть пока все на этом остается. Надо бы дальше посмотреть. Давай-ка выпишем ряд значений, развивающихся с коэффициентом этой спирали:

... — 0,236 — 0,3003 — 0,382 — 0,486 — 0,618 — 0,786 — 1 — 1,272 — 1,618 — 2,058 — 2,618 — 3,3302 — 4,236 — 5,389 — 6,856 -...

Конечно, аналогичный ряд с коэффициентом 1,272/0,786 может быть построен от любого числа. «Для удобства» мы остались в ряду золотой пропорции. И для нашей схемы мы можем взять из него подряд любые 5 членов, чтобы получить значения разворачивающейся спирали:

А теперь пойдем к нашим спиралям со стороны рядов Фибоначчи.

Посмотрите на сходящийся в ноль ряд Фибоначчи с коэффициентом j ₁ между членами ряда, например: 2 — 1,236 — 0,764 — 0,472 — 0,292 — 0,180 — 0,111 -…

Известно свойство ряда с таким коэффициентом: a_i + a_i+1 = a_i-1.

Можно записать это свойство так для 3-х последовательных членов:

Если продолжить дальше суммирование последовательных членов этого ряда, то можно заметить в этом процессе некоторые обобщения для него:

- степень числа «j ₁» равна сумме б’ольших степеней через одну, начиная со следующей:

- степень числа «j ₁» равна сумме б’ольших степеней, начиная с после-следующей:

Конечно же, интересно, а чему равна предельная сумма такого ряда?

Предыдущие суммирования (но вы это не делайте, потому что ниже увидим общие формулы) позволяют увидеть общую сумму для верхнего частного ряда: 5,236 = 2 + 3,236 = …

И при любом начальном a₀: .

Например, сумма аналогичного ряда «j ₁ — j ₁² — j ₁³ — …» равна j ₂.

Эти ряды представляют собой геометрическую прогрессию. А убывающая геометрическая прогрессия как раз является, как известно, сходящимся рядом с суммой: . Можно проверить и получить верхние формулы.

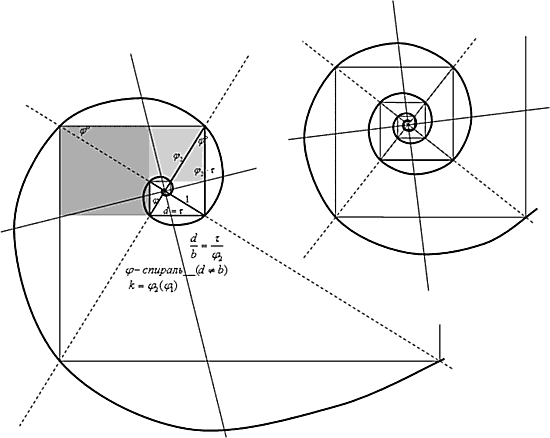
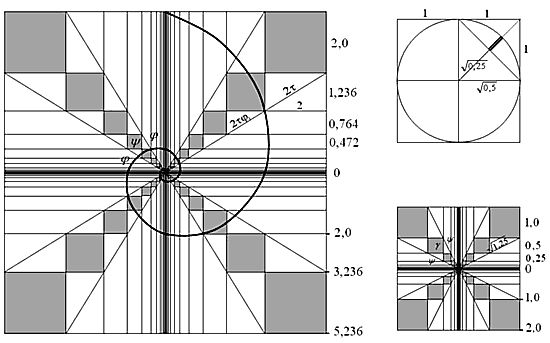
Интересно, как графически выглядит этот сходящийся ряд. Давайте посмотрим это не в линии, а на плоскости, как схождение в точку 4-х одинаковых j -рядов Фибоначчи. Образуется некая плоскость, в которой линии встречающихся рядов образуют «характерный узор».

Каждая геометрическая прогрессия имеет свою подобную плоскость. И эта плоскость формирует в себе определенную логарифмическую спираль (далее без определительного прилагательного будем говорить именно о ней), задает спираль. Эта спираль размещается в своей плоскости по центру, но с произвольным поворотом (под любым углом). (А как размещать ее точно по центру, мы увидим дальше.) На любых центральных лучах она будет отсекать отрезки, относящиеся по одному множителю – основанию (коэффициенту) спирали, отсекать шкалу значений степени этого основания. Сама такая плоскость раскрывает в себе идею спирали, содержит спираль. Поэтому будем называть эту плоскость логарифмической или спиральной. В спиральной плоскости возникает определенная «геометрия», которая выражает свойства логарифмической спирали. Во всяком случае, их легко здесь наблюдать… Вы можете даже наблюдать на «спиральных плоскостях» той или иной крутизны рельеф пересекающихся крестом долин. А спираль поднимается из бесконечно глубокого пересечения долин, каждый раз опираясь по порядку на один из 4-х гребней. Пройдя по одному гребню «серых квадратов», спираль перелетает через пропасть, чтобы опереться на следующий.

Внизу на левом верхнем рисунке — круговая j -спираль, разворачивающаяся из 0-области. Сворачивающий коэффициент j -спирали q=0,618..., и здесь он соответствует cоотношению сторон этих интересных «сереньких квадратиков».

Увеличить >>>

Увеличить >>>

На левом нижнем рисунке аналогично построена «Золотая спираль» в спиральной плоскости соответствующего ряда, например: 1 — 0,786 — 0,618 — 0,486 — 0,382 -...

Но этот ряд уже не будет рядом Фибоначчи, его q № j ₁! И здесь q=0,786 также соответствует отношению сторон характерных квадратов спиральной плоскости.

Общий член ряда:,и сумма ряда: .

(как бы 2-х рядов с шагом j ₁, чередующихся через √j ₁).

После преобразований:.

Та же сумма по формуле сходящегося ряда: .

Тогда попутно заметим здесь красивое соотношение: .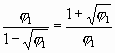

Эта «Золотая спираль» совпадает со спиралью художника, который свою «космическую спираль» нарисовал по спирали моллюска «Nautilus». И только «Золотая спираль» своим «осевым модулем» (исходным модулем качания) составляет и модуль 4-х угольной пирамиды, пирамиды «Золотой спирали»…

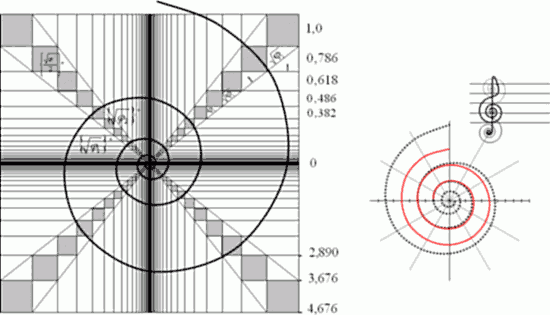
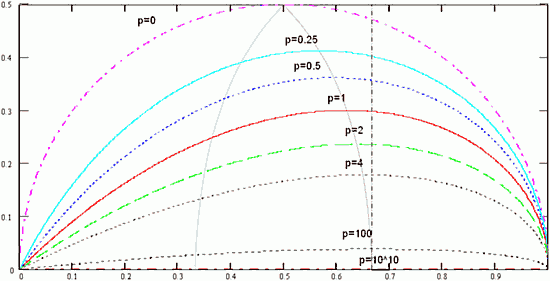
Среди множества логарифмических (или окружных) спиралей можно нарисовать «спираль силы звука» (или «децибеловую») с K=10 и .И можно нарисовать «октавную спираль» (или «дуобеловую») с K=2 и ; она показана прерывистой линией на верхнем рисунке справа внизу. Любопытно и то, как из этой спирали рисуется музыкальный скрипичный ключ…

Попробуйте нарисовать скрипичный ключ, скажем, по «золотой спирали» — получится плохо. Отношение коэффициентов «музыкальной» и «золотой» спиралей – 1,3; тогда, скажут, можно поменьше взять... С нашей же стороны – лучше не возражать мнениям, что аналогичными получатся образы ключа из бесчисленного множества близких спиралей где-нибудь в диапазоне K=1,9ё 2,1 … Постройте спирали с этими крайними коэффициентами; вы увидите насколько они менее оптимальны на нотном стане. Да и, в конце концов: среди этой группы есть только одна принадлежность одному неслучайному символу — принадлежность октаве. Эта группа – «окружение» октавы.

Скрипичный ключ – символ музыки вообще. Я не знаю, руководствуясь каким заданием или наитием, Художник нарисовал его именно таким образом. И вот такое близкое попадание в «конструкт» «октавной спирали»… Или все же — случайно?

Напомним, что есть «осевой модуль» и где он на спиральной плоскости. Вернемся к началу текущего разговора о спиралях и вспомним рисунки начала текста, где впервые мы встретились со спиралями. Тогда именно «качающиеся треугольники» («модуль пирамиды») образовали модуль осей координат именно «Золотой спирали». То есть оказались перпендикулярны гипотенуза исходного треугольника и катет второго треугольника на том же основании, который был «качнувшейся» гипотенузой. Было видно, что любая логарифмическая спираль образуется своей подобной системой пересекающихся прямоугольных треугольников; а их углы задают угол наклона «модуля осей», совпадающих с гипотенузами. Понятно, что эти треугольники, подобно изменяясь, и формируют в дальнейшем прямоугольный образ спирали, как это представлено на нижнем рисунке. Конечно, только один «модуль прямоугольных треугольников» задает одновременно и пирамиду, и спираль. Другие «модули спирали» уже не будут образованы «качающимися треугольниками». По аналогии же с метафорой «качание катет-гипотенуза» можно сформулировать метафору «действия» треугольников «осевого модуля» – «поворот катет-катет». Понятно, что пропорция (соотношение сторон и углов) этих треугольников будет общей единой и своей для своей спирали…

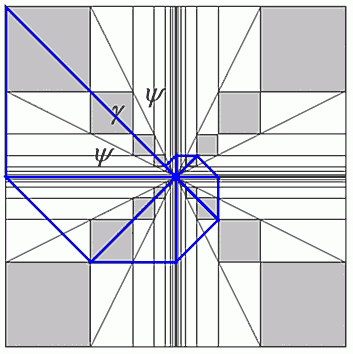
Посмотрим еще раз на 1-ую «спиральную плоскость». Вы конечно обратили внимание на углы j ° и y °, образующие в этой плоскости сходящихся 4-х j -рядов лучи как бы "мальтийского креста". Эта комбинация углов: j °, j °, и y °, — вполне "закономерно" отразились здесь. А в каком сходящемся ряду, в плоскости какой спирали на месте этих углов будет другая известная нам комбинация: y °, y ° и g ° ?

Они появятся, когда сторона меньшего квадрата будет равна половине предыдущего, когда k=0,5 и каждый последующий член ряда (не Фибоначчи!) равен половине предыдущего.

Общий член ряда: .

Такой ряд будет сходиться еще быстрее, чем j -ряд; его сумма , и сторона "суммарного" квадрата будет ровно в 2 раза больше стороны исходного. Спираль же, строящуюся на угле "y ° " по известным правилам, можно называть, например, y -спиралью.

Подобный угол у всех спиралей будем обобщенно обозначать «b ₀». А срединный угол между 2-мя этими углами, угол, раскрывающийся квадратиками «спиральной плоскости», будем называть для краткости «k -угол». Чем он больше, тем больше коэффициент «k».

Этими характерными углами «спиральных плоскостей» и задаются их «модули осей». Для указанных на рисунках спиралей «модулем осей» является та перпендикулярная пара, которая повернута от базовых 0-осей («катетовых осей») по часовой стрелке на угол b ₀. Второй «модуль осей» задает такую же, но обратную по направлению спираль. Левую спираль, которая раскручивается против часовой стрелки (как на рисунках), задает тот модуль, что сдвинут по отношению другого модуля против часовой стрелки. Соответственно, тот «модуль осей», что повернут по отношению другого модуля по часовой стрелке, задает правую спираль.

У k -угла интересное в дальнейшем значение будет иметь тот луч, который первый стоит на пути раскрывающейся спирали. Будем по аналогии с 2b -треугольниками называть этот луч Q -лучом. То есть «модуль Q -лучей» — это второй модуль, и он повернут относительно «модуля осей» на угол «k » навстречу раскручивающейся спирали. Или, по другому, — это «осевой модуль» зеркальной спирали (спирали встречной направленности).

Присутствие на квадро-плоскости 2-х углов «b ₀» напоминает о равнобедренных 2b ₀-треугольниках и его интересных свойствах (см. приложение). И то, что это вообщем-то теперь «знаменитое» соотношение «2b +k =90° » есть очередное общее выражение спирали, и каждое конкретное соотношение есть конкретная спираль. Это имеет выражение на спиральной квадро-плоскости. Любой отрезок, соединяющий точки пересечения спирали и соседних квадро-осей, во-первых, задает углы a ₀ и b ₀ с осями-катетами соответственно меньшей и большей, и во-вторых, задает зеркальный (то есть направленный в другую сторону) осевой модуль в пересечении с Q -лучом (первым по раскрытию спирали лучом k -угла)…

И остается вопрос (кому интересно): Если прямая, пересекающая спираль, не является ее лучом, то по какой зависимости изменяются длины отрезков, «нарезаемые» спиралью на этой прямой? И по какой зависимости изменяется угол наклона касательной к спирали в точках ее пересечения с такой прямой?

Давайте будем называть наши спирали по углу наклона «осевого модуля». Будем определять этот угол через его тангенс, то есть через «q». Тогда все спирали расположатся между 0-спиралью (k -угол=90°) и 1-спиралью (k -угол=0°). Возьмитесь руками за лучи срединного k -угла и начните сдвигать и раздвигать, закручивая спираль (увеличивая «q» к «1») и раскручивая спираль (уменьшая «q» к «0»)… Ну как, получается? Куда то нас приведет эта забава …

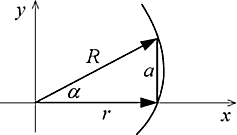
Может быть, получим пока общие характерные зависимости и общую характерную формулу логарифмических спиралей… В качестве схемы возьмем прямоугольную основу логарифмической спирали («модуль логарифмической спирали»). Как видите, она соответствует схеме начала этого текста, только повернута и введены другие обозначения.

Логарифмические спирали здесь строятся, как говорили прямоугольными треугольниками по метафоре «поворот катет-катет». Посмотрите рисунок. На нем обозначенные отрезки измеряются от центра. Вы легко можете видеть, что соответствующие (одно-номерные) «a», «b» и «h» связывают средне-геометрические отношения, как элементы в прямом треугольнике. Из этих соотношений легко найти формулу, связывающую 2 величины, например, «b» и «h». Она приведена в верхнем правом углу рисунка.

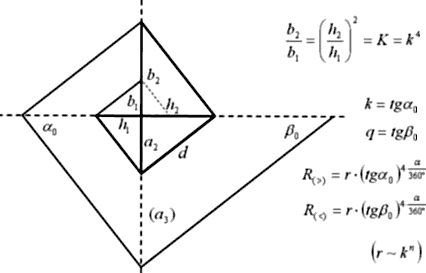
Всё множество логарифмических спиралей располагается в диапазоне углов a ₀=45° ё 90°. При a ₀=90° спираль становится лучом из своего центра, причем у левой спирали (как на рисунке) центр перемещается (по полу-окружности) в левую точку отрезка «d», а у правой – в правую. А так как спираль – плоская фигура, то есть занимает плоскость, и не имеет однозначного угла исхода из центра, то можно сказать, что в предельном случае «a ₀=90° » луч будет не один, а четыре ортогональные относительно «d». А вот о том, что происходит, когда a ₀=45°, мы поговорим дальше.

Итак, на этом рисунке мы получили формулу логарифмической спирали. Она всегда отсчитывает от некоторого r₀ ~ kⁿ. Здесь k=1/q > 1, то есть используется основание разворачивающейся спирали. В дальнейшем так и будем использовать: для акцентирования смыслов схождения спирали – Q=q⁴=(tgb ₀)⁴, а когда удобно видеть расходящееся развитие спирали – K=k⁴=(tga ₀)⁴. Зависимость с 4-ой степенью выражает 1-ое и очевидное свойство логарифмической спирали. Наши спирали называют «логарифмическими спиралями», указывая на свойство пропорционального увеличения отрезков, отсекаемых спиралью на периодически (с одним ритмом) проведенных из центра лучах. Понятно, что при пересечении одного и того же луча это будет коэффициент, равный 4-ой степени коэффициента между отрезками на соседних ортогональных (под 90°) осях. Отрезаемые спиралью на таких осях отрезки возрастают по величине, связанной с коэффициентом этой спирали. Вообще, каждый такой отрезок «d_n» у логарифмических спиралей можно составить, например, 4-мя экспоненциально изменяющимися элементами с основанием и последовательными натуральными степенями (1, 2, 3, 4). В соответствии с этим свойством на спиральной плоскости по центральным лучам всегда располагаются между витками спирали 4-е «элемента»: квадратиков, линий сетки, — и сумма 4-х соседних членов убывающей геометрической прогрессии задает расстояние между витками на оси. И формула спирали может записываться, как через «полно-оборотный коэффициент» (Q, K) так и через «орто-поворотный» (q, k), когда как удобно.

Но точно также можно попробовать построить «спиральную плоскость», например, на 5-ти осях, на 5-ти k ₍₅₎-углах, которые создаются 5-тью сходящимися рядами, расположенными по сторонам правильного 5-угольника. Получится спиральная пента-плоскость с K=k⁵… А можно построить спиральную гекса-плоскость…

Давайте здесь сформулируем по порядку основные свойства наших спиралей (опираясь на спиральные квадро-плоскости).

2-ое. Спираль «нарезает» на каждом луче отрезки по множителю «K»: d₂/d₁=K.

3-ье. Отношение любого отрезка на луче к расстоянию от него до центра спирали равно d₂/r2=K- 1(здесь «r₂» — расстояние от границы отрезков «d₁» и «d₂»).

4-ое. Отношение длин соседних участков спирали на общих их углах 90° равно «k», соответственно на углах 360° - «K».

5-ое. Витки одной спирали пересекают центральные лучи под одним углом.

Из 2-го и 3-го свойств можно закончить тему нахождения центра спирали, если известны 2 отсекаемые спиралью отрезка на луче, или отрезок и основание спирали. Понятно, что это расстояние равно сумме отрезков, меньших данного, и при решении подтверждает формулу суммы убывающей геометрической прогрессии:

В этой формуле содержится непоследнее объяснение прелести обратных величин.

Их разности с «1» равны между собой (!) в масштабе этих величин: K-1 = K(1-Q) …

Эта формула, как формула суммы, связана с геометрией соответствующей «спиральной плоскости». Например, j -спираль на квадро-плоскости, проходя через угол «серого квадрата» на Q -луче (первом по направлению расхождения спирали), пересекает квадро-оси на линиях следующего (большего) «серого квадрата»; то есть образуя на первых 2-х точках прямоугольный j -треугольник; а на всех 3-х точках и центре спирали – «осевой модуль». А в квадро-плоскости Золотой спирали образуются подобные равнобедренные треугольники, основаниями которых являются отрезки, соединяющие угол «серого квадрата», лежащий на Q -луче и точку пересечения ближайшей квадро-оси с «^ -ом» от аналогичного угла следующего (большего) «серого квадрата». В геометрии этих плоскостей можно находить еще и еще интересные частные моменты; особенно у j -спирали.

По поводу 4-го свойства. Спираль – это свернутая шкала последовательных величин «Kⁿ». Этот показатель степени «n» (который дает равные «отсечки» уже в логарифмической шкале от первой, от «природной»), и есть число витков. Мы говорили ранее о логарифмических шкалах нашего восприятия над реальным (физическим) миром. То есть в наших физиологических чувствах (не могу, правда, утверждать это по всему перечню) «заложена» спираль…

По поводу последнего свойства: двигаясь по логарифмической спирали, мы будем видеть ее центр, скосив глаза всегда на один угол (тогда удобнее идти к центру). Такой угол у окружности равен 90°, у нее разворот к центру (как и отворот) отсутствует. Чем быстрее скручивается-раскручивается спираль, тем больше угол разворота-отворота. Давайте определим угол «d » - угол между «^ » к лучу и касательной спирали в точке пересечения луча. Формула спирали известна. Из выражения при a =0 получаем . То есть, если идти по спирали к центру и держать равнение на центр, поворот головы будет отличаться от 90° на угол, зависящий от «lnk». Постоянный же коэффициент «2/p » - это «h/b» p -пирамиды; и это еще величина – обратная ј круга (90°). По этой формуле, например, для окружности (k=1) tgd =0, то есть касательная перпендикулярна радиусу. Для j -спирали d » 17°, для Золотой спирали d » 8,7°.

Посмотрим дальше неочевидные свойства.

1. Биссектриса орто-витка делит его на участки в отношении «Ц k», а базу этого витка (гипотенузу на катетах-осях «r₁» и «r₂») в отношении «k». При этом 3 радиуса, ограничивающие эти участки, будут находиться последовательно в пропорции «Ц k».

А в самом общем случае – если прямой угол орто-витка разделить на «n» равных углов, то получающиеся при этом участки витка будут находиться в пропорции «» между соседними. Или по другому: участки спирали, ограниченные одинаковыми центральными углами, имеют один коэффициент изменения длины.

При этом базовая гипотенуза орто-витка при «n>2» делится уже в какой-то своей неодинаковой и возрастающей пропорции. А то, что гипотенуза делится биссектрисой на части, пропорциональные катетам, - это, может быть, важнейший системный эффект именно прямоугольного треугольника. Следствием его является, например, то, что биссектрисы противоположных углов «сдвоенного квадрата» (прямоугольника 2:1) создают на диагонали триаду равных отрезков. Второй случай формирования «триады отрезков» мы увидим во «встрече с А.П.Саврухиным».

Посмотрите это свойство на нижнем рисунке, на правой схеме.

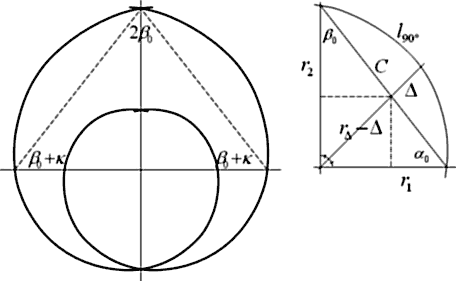
Правая схема позволяет сформулировать новые не менее неочевидные свойства спиралей. Приведем исходные зависимости:

Опираясь на них, можно получить уже некоторые характерные соотношения. Приведем, что получается для величин верхней схемы. После каждой зависимости приведем в скобках соответствующие значения (округленные) для последовательно: окружности, Золотой спирали, j -спирали, - относительно значения для окружности. (Эти же формулы работают и для окружности при k=1.)

Верхнее выражение, интересное само по себе, как квадратный корень из суммы взаимообратных чисел, имеет конкретный предметный смысл в мире спиралей!

И здесь возникает еще нечто. Исходя из «предметности» смысла подкоренного выражения, его «константности» для определенных спиралей сформулируем для взаимообратных:

Вот такие «первертыши», которые мы уже видели в формулах для ВО-прямоугольника… Так вот в чем секрет этого! ВО-прямоугольники с W -линией основаны на «взаимообратности»!...

И мы ранее определили некое «обобщение» для некоторых взаимообратных величин, в ряду которых есть и Золотая пропорция: . Не правда ли, между этими выражениями возникают «неясные параллели», «туманные аллюзии»… Во всяком случае, давайте зададимся вопросом: какой «представитель» этого последнего выражения является и «представителем» в мире логарифмических спиралей»?

Исходное уравнение для ответа на этот вопрос: . Тогда через выражение «y²–y–1=0» получаем k = Ц j ₂. Вот так. Это и есть Золотая спираль. О чем раньше мы просто «догадывались», то есть выделяли ее, как гармоничную. Да встречали её повсюду, как основу биоформ…

Дальше.

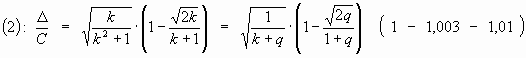
Обратите внимание, что для подавляющего количества «нормальных» спиралей это соотношение как раз и составляет ~0,21. Например, при k=3 (K=81!) оно равно ~0,2123 (~max); при k=4 D /C» 0,2107, при k=5 (K=625!!) D /C» 0,2074, при k=10 D /C» 0,187, при k=100 D /C» 0,086 …

Следующее. (Интересно – отношение величин выражается разностью…)

Сопоставляя (1), (2) и (3), получаем:

Для последней формулы конкретные величины относительно значения для окружности составят: у Золотой спирали ~ 1,29, у j -спирали ~1,57. Но поразительна сама эта формула. Смысл ее в следующем.

2. У всех логарифмических спиралей на биссектрисе орто-витка отношение возвышения (подъема) витка ко всему «радиусу» равно выражению, в числителе которого находится разность «k» и аналогичного возвышения орто-витка окружности «R=Ц 2», а в знаменателе – сумма «k» и «1» (оставшейся части R=Ц 2).

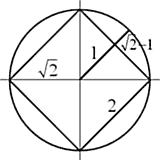
Все логарифмические спирали связаны с этой окружностью!.. Парадоксально… Странный, непонятный факт… Этот факт станет еще более многозначительным, когда во «встрече с А.П.Саврухиным» мы увидим подобную схему еще 2 раза (вторая – в 2 раза меньше…).

Посмотрим, похоже, еще некоторые частные свойства.

3-а. Отношение длины орто-витка j -спирали к расстоянию до центра спирали от начала витка равно «2»: (?).

3-б. Отношение длины 45° -витка Золотой спирали к расстоянию до центра спирали от начала витка: (?).

Это пока предположения, сделанные из наблюдения. Чтобы их проверить, надо найти формулу зависимости между длиной участка спирали и его опорным радиусом (от которого он разворачивается). Но прежде чем мы приступим к этому, найдем ещё один повод.

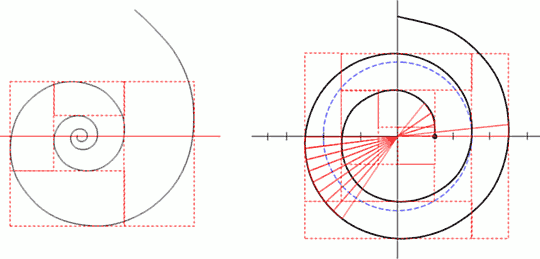
Мы уже видели в начале, что шкалы на лучах из значений показательной функции «aЧ kⁿ» имеют конечную длину, как убывающие геометрические прогрессии. А витки спирали, стремящиеся к центру?.. Они – это тоже свернутая шкала по тому же основанию «k». Получается, что от какой-то своей точки до центра логарифмическая спираль имеет конечную длину?!.. И тогда длина какой-то спирали может оказаться равна длине окружности, в которой эта спираль оказывается. Так, как это изображено ниже на левом рисунке.

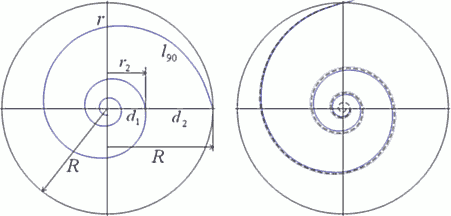
Причем понятно, любая проведенная окружность будет заключать в себе равную по длине такую спираль. Так какое основание «k» у этой спирали?

Давайте обозначим отношение орто-витка и общего с окружностью радиуса, ограничивающего этот виток с большей стороны, например, так: z=l₉₀/R. Тогда отношение орто-витка и его опорного радиуса: l₉₀/r=zЧ k. А например, для отрезка на луче:l₉₀/d₂=z/(1-Q).

Общая длина спирали, как убывающей геометрической прогрессии от максимального орто-витка: L=l₉₀/(1-q). Сравним ее с длиной окружности:

или .

Попутно заметим отношение длины полного витка к его большей четверти и к меньшей четверти:

и

И вернемся к определению длины участка и всей спирали. Теперь у нас достаточно поводов для этого.

Для определения длины участка (от угла до угла) можно воспользоваться известными формулами для длины дуги в полярных координатах или в параметрическом представлении «x» и «y» (в проекции на оси). Взятие интеграла дает формулу:

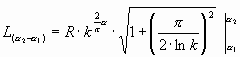
Обратим внимание на подрадикальное выражение. Это – . И закончим выражение длины участка при a ₁=0: 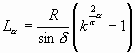. Отношение длины орто-витка к опорному радиусу (с которого раскручивается конкретный участок) тогда равно: .

Теперь определим «равно-окружную» спираль.

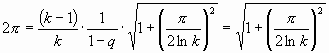
Откуда и .

Причем её .

Подставив значения, получим: k=1,2881766…, d =9,15785…°. То есть эта спираль чуть-чуть «размашистее» Золотой спирали. «Равно-окружная» спираль изображена на правом верхнем рисунке сплошной тонкой линией, а «Золотая спираль» – пунктирной.

Это свойство равенства длины окружности и заключенной в ней одной из спиралей было известно еще в XVII веке. А Якоб Бернулли, живший в это время, изучавший свойства логарифмических спиралей и восхищавшийся их гармонией, завещал даже изобразить спираль на надгробном камне.

Так, а что со свойствами 3-а и 3-б? У j -спирали отношение «l₉₀/r₀» оказалось равно ~2,11; а ровно «2» - у спирали с k» 1,5 (~0,03%). Отношение «l₄₅/r₀» равно «j ₂/2» у спирали с k» 1,11. У Золотой же спирали это отношение – больше (~4%); у нее же отношение на прямоугольном витке равно ~1,8.

Посмотрите на 4-ое (из основных) свойство спиралей. Его можно обобщить так: отношения длин соседних участков спирали одинакового угла поворота одинаковы и равны некоему «k». В том числе и по этому можно задаться вопросом: а какие соседние участки спиралей, на каких углах равны между собой? Ведь у любой спирали, получается, будет некая общая по ее виткам зависимость: равенство длин каких-то «соседних» участков спирали будет повторяться на определенных соотношениях их углов…

У j -спирали здесь получается так, что длина «старшего» участка на углу 90° равна длине «младшего» на углу 180°. Но вот для Золотой спирали равными являются, похоже, длины «старшего» участка на углу (90)° и «младшего» на углу (90+45)°, но с зазором между ними в 45° … Посмотрите, как это выражается на следующих рисунках.

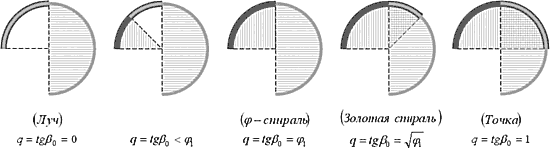
Но не спешите присваивать конкретный образ (луч и точка) для 0-спирали и 1-спирали. Здесь есть парадоксы. Правда, это больше парадоксы «точек зрения».

Помните (?), мы сжимали-разжимали спирали, взявшись за лучи k -угла… Снова взявшись за лучи k -угла, разведем его на 90°, а потом сведем вместе:

Прокомментируем. Конечно, строкой «здравого смысла» является 1-ая строка. «Окружности» 2-ой и 3-ей строки и есть точки при r=0. А вот по столбцу «0-спирали» получается, что формула спирали с разворачивающим коэффициентом более адекватна. По этому же столбцу посмотрим последние 2 строки.

С уменьшением прилегающего угла (b ₀) и соответствующим увеличением «k» все круче, с более дальним загибом уходит ветвь спирали, становясь в пределе, если смотреть от центра, бесконечным радиусом (лучом). Но проще смотреть не из центра, а с периферии («знать бы это политикам»…). И тогда все окажется по другому.

При k=Ґ меньших квадратов нет, есть только один квадрат, весь ряд — только «1» и «0», а прилегающий угол равен «0». И формирующаяся в 4-х квадратах кривая никогда не сойдется в центр. Она станет окружностью (по характеризующему углу ее и называем «0-спиралью»). Возвышение линии окружности над линией между точками пересечения "осей" (расположенное на биссектрисе) легко посчитать: . Это же значение дает, как помним, и формула «D /C» для спиралей при k=1. Так спираль разве – окружность в каких-то своих отношениях или пределах? …

«Спираль – это одухотворенный круг. В спирали круг расцепляется, разворачивается, перестает быть порочным – освобождается». Это слова беллетриста В.Набокова…

Ну что ж. У нас есть формулы длины участка спирали, и мы можем проверить предполагаемые свойства аналитически. Еще раз повторим, что указанные правила «наложения секторов» должны работать, естественно, на любых участках. Это общее свойство, отличающее одну спираль от другой.

Мы знаем, что длины участка спирали напрямую связана с радиусами, которыми он ограничен. И взаимоотношения участков напрямую связаны с отношениями соответствующих радиусов. Отсюда сразу можно убедиться в правильности центрального рисунка. По нему для опорных радиусов j -спирали можно записать: k²=k+1. А это и возможно, лишь когда k=j ₂.

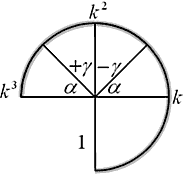
Составим алгебраические соотношения для всех случаев (см. схему), исходный r=1.

Для правых рисунков: в формулах длин участков, радикалы будут сокращаться. Тогда исходная формула:

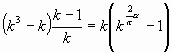
И после преобразований: .

Для левых рисунков аналогично получаем: .

Интересно привести значения углов «a » для разных «k».

Для kЈ j ₂ (угол измеряется от правой части горизонтали):

a =90°: k» 1,618034

a =45°: k» 1,26278

a » 34,9°: k» 1,200 ()

a =30°: k» 1,17041

a =18°: k» 1,10081

a = 9°: k» 1,05010

Итак. Для j -спирали все оказалось, как и предполагалось. А вот для Золотой спирали (k» 1,272) так не получилось. Оказалось, что длина, равная длине орто-участка спирали, находится на ближнем к центру участке на углу ~(90+46,4)° ? То есть на ~1,4° больше, чем «наблюдалось». Рисунок вообще-то можно не менять из-за незаметности этой величины. А вот знание – есть знание… Эта спираль с a =45° изображена на том же правом рисунке с Золотой и равно-окружной спиралями точечной линией (более «собранная» спираль). Видите, как близко Золотая спираль «устроилась» между этими 2-мя по своему замечательными спиралями…

Ну, и кстати, чему равен схемный угол «a » у «равно-окружной» спирали (k» 1,288)? Он равен ~48,9°.

Для kі j ₂ (угол измеряется от левой части горизонтали):

a =90°: k» 1,618034

a » 49,5°: k= Ц 5» 2,236

a =45°: k» 2,35364

a » 34,5°: k=e» 2,718

a =30°: k» 2,93245

a =18°: k» 3,91373

a = 9°: k» 5,94946

Ну и конечно, эти две формулы можно попробовать представить одной, измеряя углы от вертикали (± g).

Общая формула для углов от вертикали: , где знаки в степени:

«+» - для углов в «старшую» сторону (спирали с k>j ₂)

«- » - для углов в «младшую» сторону (спирали с k<j ₂).

После этих абстрактных выкладок, чтобы не забыть или не запутаться в смыслах, повторим, о чем говорят эти формулы и эти углы в секторах. На верхних рисунках даны схемы общего свойства, что любая спираль имеет равенство длин соседних участков за вычетом угла «g »:

- при k<j ₂: «старшего» участка на углу 90° и «младшего» участка на углу «180° - g » (g =0ё 90°),

- при k>j ₂: «старшего» участка на углу «90° - g » (g =0ё 90°) и «младшего» участка на углу 180°.

И тогда можно одной формулой выразить зависимость от «k» значения угла, задающего равенство участков спирали. Для любого из углов «a » или «g », отсчитываемых от своего луча:

, где «n» - цифровое слагаемое в степени у «k» в связанных формулах, которые приведены выше; «n» связано с лучом, от которого ведется отсчет схемного угла: =1 для правого горизонтального, =2 для вертикального, =3 для левого горизонтального.

Будем обозначать угол, представляющий каждый свою спираль (характерный угол) в общей формуле через «± g _k».

И может быть сами эти алгебраические выражения дают ответ на детский вопрос «почему»: почему соотношение именно этих секторов выстраивают равенство соседних участков всех спиралей? Именно общая часть всех предыдущих выражений «k^3- k²+1» является как бы «алгебраической иллюстрацией». Обобщенная схема этих формул «k^{3 -} k² = k^{«a » -} 1» содержит в левой части как раз 3-ий от «1» по возрастанию спирали прямоугольный сектор (см. предыдущий рисунок). Он и задает все отношения.

Ну и последние факты и выводы из этих отношений. При предельных значениях – все формулы дают окружности… Далее. Получается, j -спираль делит всё множество логарифмических спиралей на 2 группы по степени ускорения разворачивания-сворачивания. По этому признаку их можно называть «до-фитовые» (то есть медленно изменяющиеся) и «после-фитовые» (быстро изменяющиеся). А вообще диапазон нормальных (непредельных) спиралей можно определить по a =18°: k = 1,1 ё 4.

Есть здесь одна «параллель». Соотношение длин соседних участков спирали связано еще вот с чем. Из диалога «Тимей» мы знаем идеальную пропорцию Платона для последовательных a- b- c- d: . Это – геометрическая прогрессия, и aЧ d=bЧ c=a^2Ч p³, а среднее геометрическое этой последовательности: aЧ Ц p³. И эта последовательность есть отношение последовательных участков логарифмических спиралей, образованных на одинаковых углах. Лаконичным же символом (образом) этого является полный виток спирали, разделенный орто-осями на 4 участка.

Давайте вернемся к нашим спиралям. При решении предыдущих вопросов, связанных с длиной спирали, у меня образовались нагромождения и сомнения. Спасибо старому товарищу. Откликнувшись на просьбу пройти по этим местам, он пошел «радианной» тропой. Решением длины участка спирали на углах измеряемых в радианах над натуральным основанием «e» он помог разрешить мои сомнения и отбросить нагромождения. И именно сопоставление результатов позволило увидеть еще нечто. Сейчас об этом расскажем. Но прежде посмотрим, как сопоставляются у одной и той же спирали разные основания, по которым она может быть описана.

Одна и та же спираль может строиться на любых коэффициентах «k». Вопрос в том, на каком углу (части круга) значение степени получается «1», и спираль «получает» чистый множитель «k»; или по другому – сколько раз укладывается такой угол (дающий степень «1» для «k») в полном круге?... То есть мы можем выразить какую-то спираль при ее неизменном «K» (круговом коэффициенте полного оборота) любой парой: основания «» и угловой меры (единицы) «ue =1/e ». Ведь известно соотношение . И тогда мы имеем орто-основание k_оє k₍₄₎, или радианное основание k_рє k_(2p), или какое-то другое. Выразим соотношение этих оснований-коэффициентов (при одной угловой мере!) формулой: . Из получаем также такое соотношение: . Здесь отношение e 2/e 1 – это соотношение 2-х угловых мер на одном углу, например, на круге. На самом деле, ведь - . Для выражения какого-то k₍₄₎ через k_(2p) это будет .

И соответственно у 2-х разных спиралей может быть одно основание, но при этом с разным множителем у угла в выражении степени или по другому – с разной угловой мерой. Обычно универсальным основанием, из-за простоты выражения степени, является «e».

Итак, для одной и той же спирали угловая мера и основание – неразрывная пара. И таких пар – множество. Переход к другой угловой мере – это переход к другому основанию: . Для конкретной спирали оператор перехода по основанию есть оператор перехода по угловой мере: . Вот соотношения, выражающие это.

Но интересно отметить отношения для одной и той же спирали между орто-основанием с угловой мерой в долях круга, выраженных через p, и между основанием «e» с множителем в выражении степени, устанавливающим переход к радианной угловой мере.

Вот математическая цепочка: . Здесь угол «a » - угол в радианах. И тогда для данных выражений «tgd » - оператор перехода между основаниями. Тем самым из всех оснований выделяются в особенные и взаимосвязанные орто-основание (4-х осевое основание) и основание «e», связанное с радианной мерой (с количеством осей на круге — 2p, более 6).

Давайте посмотрим теперь решение длины участка спирали, полученное приятелем в радианной мере. Итак, для спирали, выраженной, как получается:

.

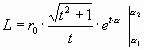Первое, что заставляет «вздрогнуть» - это выражение «» …

При r₀=1, a ₂=0 и получаем . Это выражение, мы знаем, порождает одно из пары взаимообратных чисел (см. текст «О взаимообратных числах»), а при t=2 дает «j ₁». Интересно – у какой это спирали?

Теперь давайте вспомним, что такое «t»? Как видели в верхних преобразованиях, . Тогда формула участка спирали в радианной мере: . А угол «a ₁» можно выразить так: .

Понятно, что в принятых соотношениях углов (a ₂=0) радиус «r₀» ограничивает участок спирали со стороны, противоположной центру спирали. Если «r₀=1» - это радиус, ограничивающий участок спирали со стороны ее центра, то на том же углу «D a » (иa ₂=1/t) получаем . Интересно увидеть, как получается это соотношение. Зададимся им изначально и представим, как разность: . Первое значение получается из исходного выражения взятого определенного интеграла (при r₀=1) при значении a ₂=1/t. Для вычисления угла, при котором получится второе выражение в разности, составим уравнение: . После преобразований получим: . Интересно, что угол этой разностью сам показал свои взаимосвязи.

Итак, есть 2 участка одной спирали, связанные в своем определении с одинаковым характерным углом «D a є a j », которые отличаются по длине в «e» раз … И у каждой спирали есть свой такой характерный угол. И всё это «происходит» на формуле для Золотой пропорции…

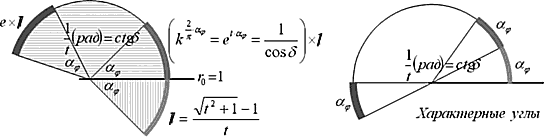
И эти формулы связаны с «касательным углом» - углом между касательной к спирали и центральным лучом, проходящим через точку касания. В наших обозначениях угол «d » - угол с перпендикуляром к лучу. Более того, между этими углами наблюдается почти прямая зависимость при k<2: d » 2Ч a j (чем меньше основание «k», тем ближе к «2» сверху) …

Сделаем обобщения.

1. Каждая спираль имеет характерный угол , на котором два соседних участка относятся друг к другу, как «1/cosd »; а меньший из них меньше в «e» раз участка, начинающегося от его начала через угол 1/t (рад) = ctgd (рад) и опирающегося на тот же угол «a j ».

2. Если радиус спирали, разграничивающий 2 характерных соседних участка равен «1», то длина начального (меньшего) характерного участка вычисляется по формуле обобщенных взаимообратных чисел с параметром «t», равном котангенсу «касательного угла» спирали.

Например, этот участок равен «j ₁» у следующей спирали: lnk=p, k= ep » 23,1407, d ={2}° » 63,435°, a j = ln(Ц 5)/2 » 0,40236(рад)» 23,0535°.

Посмотрим движение этих взаимосвязанных параметров в таблице.

k	t	Угол d	Угол a j	Угол 1/t	Кратность хар-х углов	L мл. участка	Отношение 1/cosd
1,1	0,06068	3,47224	1,73506	944,28528	544,23868	0,03031	1,00184
1,2	0,11607	6,62067	3,30295	493,63335	149,45239	0,05784	1,00671
1,27202	0,15317	8,70856	4,33744	374,05565	86,23883	0,07614	1,01166
1,61803	0,30635	17,03239	8,38851	187,02782	22,29572	0,14974	1,04587
2	0,44127	23,81049	11,55028	129,84255	11,24151	0,21083	1,09303
2,71828	0,63662	32,48164	15,31080	90	5,87820	0,29130	1,18545
5,14358	1,04262	46,19544	20,21624	54,95343	e	0,42649	1,44467
7,83853	1,31083	52,66093	21,85473	43,70946	2	0,49489	1,64872
10	1,46587	55.69865	22,41639	39,08650	1,74366	0,52834	1,77448
22,435	1,98028	63,20722	23,05417	28,93312	1,25501	0,61529	2,21845
23,14069	2	63,43495	23,05350	28,64789	1,24267	j 1	Ц 5
53,00765	2,52766	68,41510	22,66753	22,66753	1	0,67979	e
100	2,93174	71,16579	22,09613	19,54325	0,88447	0,71548	3,09760
1000	4,39761	77,18901	19,62495	13,02883	0,66389	0,79813	4,50988

Сделаем самые общие выводы по динамике спиралей и закончим тему на этом. С увеличением «k», с ускорением раскручивания спирали для достижения на характерных углах «a j » и «1/t» соотношения «e» эти углы всё более сближаются, становясь равными при k» 53. Тогда окончание большего из «соседних участков» (c соотношением 1/cosd) совпадает с началом участка «e»; кратность по углам «a j » и «1/t» n=1, и спираль при этой кратности разбивается на последовательные участки «a j ».

Но интересно то, что угол «a j » имеет максимум своего изменения около значения k» 22,435, образуя своими значениями (от аргумента k) «горку» с подъемом на нее из начала координат и очень пологим спуском в «0» на бесконечном «k». На аргументе «t» происходит аналогично, но гораздо быстрее (сжато по оси ординат). После максимума уменьшаются и «a j », и «1/t»; и последний – быстрее. На «n<1» участки пересекаются, заходят один на другой. Сохраняется лишь отношение «e» этих участков.

Относительная динамика с ростом «k»:

Вывод.

Наиболее разнообразные спирали располагаются на малых «k». Как и раньше при аналогичном сопоставлении углов в орто-осях можно утверждать, что основные спирали располагаются в диапазоне k=1,1ё 4, на кратности характерных углов n>4. Но по признаку «угол ¹/_{t і} 90° » (и меньше 1,5 круга) диапазон «нормальных спиралей» можно уменьшить до .

Пара основных форм представления логарифмических спиралей: в орто-осях и в радианах, - представляют по-своему, но каждая элегантно, единое свойство спиралей – определенное соответствие длин старшего и младшего участков. Представление в орто-осях показывает это свойство через равенство таких участков, задавая для каждой спирали свой угол в единой схеме соотношения участков. Эта форма наиболее осязаемо: на «разбегании» равных участков, - задает «скрученность/раскрученность» спиралей и разделяет их на до-фитовые и после-фитовые (см. выше).

Представление на основе «e» в радианах (в 2p -осях) сравнивает разные спирали в общем их свойстве на сопоставлении характерных углов каждой. 2 смежных участка на первом угле имеют соотношение длин, взаимосвязанное с «касательным углом» спирали. Да плюс еще наличие участка, кратного по «e».

В первой форме представления откладыванием от радиуса угла «± g _k» задается младший до противоположного радиуса участок спирали, равный участку «90° », старшему от исходного радиуса. Во второй форме представления откладыванием от радиуса в обе стороны углов «a j » задаются участки, соотносящиеся по «cosd ».

Имеют ли другие представления, на других основаниях и угловых мерах аналогичные свойства? Да. Потому что это свойство спиралей, а не просто представления. Можно поискать их для 3-х или 5-ти осевого представления. Но они едва-ли будут столь изящны или взаимосвязаны по параметрам, как орто-представление и радианное.

Напоследок еще раз, совсем уж явно и прозрачно увидим взаимосвязь 2-х главных углов логарифмических спиралей: a j и d (и не будем забывать, что есть еще 3 важных угла: 1/t (рад), ± g _k и b ₀={k}° со связанными с ним a ₀ и k). Напомним, что tє tgd, что радиус между соседними участками считаем здесь r₀=1, что общая формула длины участка: .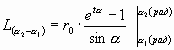

Тогда на характерном углу «a j » длина младшего участка (ближнего к центру):

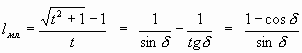
А на том же углу длина соседнего по r₀=1 участка (старшего):

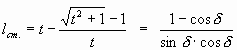
Вообще то формула длины участка спирали имеет интересную внутреннюю особенность, связанную с «sin» в знаменателе. Ведь по формуле получается, что чем больше «d », то есть более «раскрученная» спираль, тем меньше участок спирали на одном и том же его опорном углу!?... А все дело в том, что этот «синус» выполняет «сдерживающую» роль для стремительно изменяющегося основания «k» показательной части формулы.

Мы знаем: или . Известно также соотношение: tga > a > sina, где угол «a » — в радианной мере. Всё вместе в полном соответствии со смыслом и дает то, что с увеличением угла «d » длина участка спирали по вычисляемой формуле тоже увеличивается, потому что числитель увеличивается быстрее знаменателя.

А вот то двойное неравенство довольно интересно. В предельно большом для себя значении оно дает: Ґ > p /2 > 1. А вот, стремя угол к «0», мы получаем следующие приближения с количеством нулей и правильных цифр после запятой (2n+2n) в обоих случаях:

и , где nЈ -1 – значение порядка в сравниваемых величинах (в работе с алгебраическими записями этот знак должен использоваться). То есть мы рассматриваем эти соотношения на углах меньше 0,1 (рад) » 5,7°. Погрешности, например, для «tga /a » здесь такие: при a » 10° d » 1%, при a » 1° d » 0,01%. Такое быстрое уменьшение погрешности и видно из величин «n» в верхних соотношениях.

Интересно и то, что дроби в значении погрешности (в формулах над знаками примерного равенства) «⁸/₉» и «³/₄» - это обратные отношения 2-х первых основных музыкальных интервалов, на которых строятся все остальные (см. «Гармония звуков…»): секунды и кварты.

Эти неравенства, как никакие другие аргументы, говорят об органичности именно «радианной» меры для измерения углов… Мера углов в радианах дает и другие интересные приблизительные соотношения. Например, tg(Ц j ₁) » 1,0015. Здесь «Ц j ₁» задает значение угла. Но и наоборот, когда «Ц j ₁» задает значение тангенса, в результате будет тоже почти «1»: ; так что окружность составляется примерно из 3p «золотых углов».

А арктангенс числа «е» в радианах отличается от самого числа «е» почти ровно на 3/2:

.

Вообще, градусная мера выбрана не очень удачно делением окружности на 360 частей. А конкретнее, такое деление – на 2-ом месте после деления на 600 частей. Вот некоторые «плюсы» последнего.

1. Соответствие циферблату часов.

2. Более мелкая (0,6 от существующей) градусная сетка, необходимость в чем ощущается.

3. Близость этой меры к радианной (1 ^(о)» 0,0105 рад), чем лучше со-ощущаются обе меры.

4. Более удобная и взаимосвязанная цифровая форма важных углов:

а) 45° є 75^(о), 36° є 60^(о), 30° є 50^(о), 18° є 30^(о), 9° є 15^(о),

б) {Ц j ₁}° » 38,2°, а {Ц j ₁}^(о) » ^0,06% » 20/p.

5. Сумма углов треугольника – 300^(о).

Но об этом можно только говорить…

Есть некая странная «родственница» логарифмических спиралей. Она нарезает на осях одинаковые отрезки. Здесь вдоль осей-биссектрис квадрантов идет серия (ряд) одинаковых квадратов. То есть в спиральной плоскости она представляется и формируется не расходящимися парами лучей и, соответственно, рядами бесконечно увеличивающихся (и уменьшающихся) квадратов между ними, а параллельными парами лучей, не сходящимися в центре, и, соответственно, одинаковыми квадратами между ними. Естественно, что эта спираль останавливается на расстоянии от центра, равном стороне предельного квадрата (который здесь существует и равен всем остальным), или по другому – равном одному и тому же расстоянию между витками этой спирали.

Останавливаясь на едином межвитковом расстоянии (на едином шаге) от центра, эта спираль тем самым указывает на как бы определенную ширину своих витков, на как бы витки из полосы. То есть эта спираль имеет какое-то отношение к площади? И это на самом деле так. (Кстати, дорожки на всяких информационных дисках являются такими спиралями.) Витки этой спирали будут тем плотней (и нарезаемые на осях отрезки тем меньше), чем ближе параллельные лучи в квадрантах. В бесконечном пределе лучи сольются в одном множестве бесконечно малых «квадратиков», а витки образуют тем самым сплошную плоскость, плоскость круга.

Площадь круга задается в пределе витками монотонной спирали на множестве бесконечно малых квадратов в лучах середины квадрантов. Раздваиваясь, они разрывают монотонность бесконечно плотных витков. А, расходясь на угол, «создают» логарифмические спирали: сначала с очень плотными витками, но уже не монотонными, а обретающими стремление. И потом, всё раздвигаясь и распрямляя витки спирали, достигают угла между собой 90°, достигают предела разреженности и «разрывают плоскостность, создавая линейность».

Как же можно назвать такую монотонную спираль? Конечно же, ее можно назвать «площадной спиралью». Но, наверное, ее лучше назвать «круговой спиралью», а, исходя из такого подхода, логарифмические можно также обозначить, как «окружные».

Мы еще поговорим о круговых спиралях и их особенностях. Время этому дальше - во «встрече с А.П.Саврухиным». И нам, прежде, чем мы вернемся к спиралям, придется сделать далекий «экскурс». Надеюсь, само по себе это будет интересно и оправдает путь к 2-м небольшим целям. А дальними целями являются нахождение символа и еще одного объекта, в котором «движутся», взаимодействуя, радикалы из чисел.

Есть такой физик и даос – Саврухин Анатолий Петрович. Он написал книгу «Природа элементарных частиц и золотое сечение» (Изд-во МГУЛ, Москва, 2004). Если не вдаваться здесь в подробности физики, то можно сказать так. Распады частиц можно представить на плоскости в виде череды векторных треугольников, образованных энергиями исходной частицы и продуктов распада. Множество реакций 2-х частичного распада задают некое «энергометрическое множество» результирующих векторов и соответствующее геометрическое место точек конечного положения результирующего вектора. Область конечных состояний ограничена некоторой кривой. Вот она то нас и интересует. Эта кривая строится относительно полу-окружности, задаваемой единичным диаметром на оси «Х», как полу-окружности прямоугольных энергетических треугольников исходной частицы; именно «катет»-вектор исходного энерго-треугольника, исходящий из начала координат является «гипотенузой» энерго-треугольника результирующей частицы, «катет»-вектор которого, также исходящий из начала координат, и задает конечное состояние. Точнее, здесь не нужно; хотя и энерго-величины основных реакций образуют сами по себе «золотые соотношения» погрешностью на уровне погрешности эксперимента (меньше 0,02%).

Так вот, кривая конечных состояний, построенная на полу-окружности (от энергетического «катета-гипотенузы») сама по себе уникальна по создаваемым эстетическим образам (но об этом в другой раз). Построенная же относительно оси «Х» (чем мы как бы получаем ее «чистую геометрию») она образует кривую, напоминающую половину медиатора (плектра для щипковых струнных инструментов).

Посмотрите рисунок из книги А.П. Саврухина. Здесь начинаются чудеса. А.П. Саврухин нашел геометрическое построение симметричной части медиатора и то есть соответствующий геометрический смысл. И этот смысл оказался связан самым непосредственным образом с Золотой пропорцией. Как он это нашел, каким наитием, я не знаю… Наверное, путь, которым он шел, был его путь.

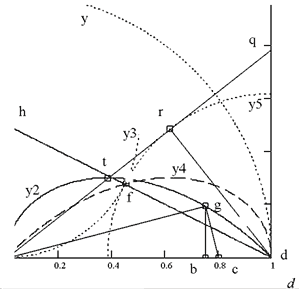
Помните (?), классическую схему геометрического построения Золотой пропорции – на прямоугольном треугольнике 1:2 переносом двумя радиусами с формированием конечной величины «Ц 1,25–0,5». Смотрите эту схему на верхнем рисунке: треугольник adh, ad=1, ah=Ѕ, y3 и y5 – первая и вторая строящие окружности. Отрезок Золотой пропорции образуется точкой «f»: fd=j ₁. Подобное классическое построение можно повторить для случаев другого положения точки «h» на оси ординат: ah=0ё Ґ. Тогда множество точек «f» сформируют кривую «y4», которая есть геометрическое место точек (образ) некоего гармонического деления гипотенузы hd в зависимости от соотношения катетов, от величины угла. Кривая «y2» — это кривая, зеркально повернутая относительно вертикали.

Симметричные относительно вертикали (x=0,5) кривые y2 и y4 образованы (в определенном диапазоне «X», например, 0ё 1) множеством точек пересечения отрезка, проходящего от одной точки границы диапазона на оси OX (y=0) до точки «h» на другой границе диапазона «X» с ординатой y=h, и окружности R=h с центром в этой точке «h». Для y4 центр окружности (точка «h») находится на оси OY (x=0), а для y2 – на линии «x=1».

Интересно внимательнее рассмотреть медиатор Саврухина. Он образован кривой y2 (или y4). Вот с этих исходных кривых и начнем.

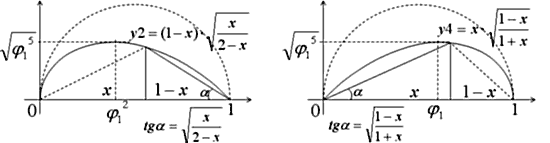
Посмотрите на рисунки. Фактически формулы этих кривых есть выражения тангенсов углов между осью Х и отрезком, соединяющим произвольную точку на кривой с ее «острым началом». По этому признаку это «острое начало» можно определить просто «началом кривой». Нетрудно посчитать угол касательной к оси Х в начале и конце этих кривых (как обычно, взяв производные). Они составляют 45° в начале и 90° в конце кривых. «Y2» и «Y4» — это кривые, которые при углах касательных на концах своего диапазона «Х» в 45° и 90° имеют оптимально равномерную кривизну для минимального расстояния от оси Х. И этот смысл означает (задает) их «природное качество» (о чем чуть ниже).

Вообще, вид этих формул прямого и обратного медиаторов (особенно тангенсов углов, как сущностных), сам вид указывает на принадлежность к славному семейству Золотой пропорции через уже известные замечательные выражения, связанные с ней. Подставьте в формулы «x=j ₁». В одной вы увидите «t » и смыслы, связанные с ней.

Заканчивая с отдельными кривыми, укажем на то, что все вписанные в них треугольники имеют углы на кривой больше 90°. Теперь еще раз посмотрим на соответствие между «медиатором» и «китом». Формирование их прямоугольными треугольниками является разновидностью триадного формирования.

Согласно исходному физическому смыслу эти треугольники с-троят из конца медиатора. Давайте посмотрим на геометрию медиатора также с другой стороны, и вот в каких аспектах. Прямоугольные треугольники внутри медиатора могут занимать ряд последовательных положений. А в каком диапазоне, и с какими соотношениями «a:b» может меняться их гипотенуза?

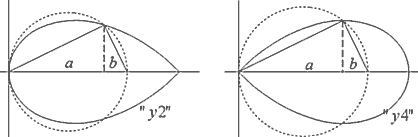
Понятно, что и в случае «y2», и в случае «y4» треугольники изменяются по некоторой зависимости (функции) a/b от «c=a+b» (или D окружности). Так на всем ли диапазоне x=0ё 1 может быть эта «с», и как меняется характер отношения «a/b»?

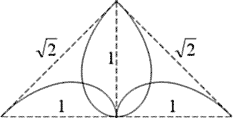
Посмотрим сначала случай «y2». Развитие вправо ограничено тем, что касательная в точке начала медиатора имеет наклон 45°. А угол наклона катета внутреннего треугольника со стороны «b» стремится к 90°. Гипотенуза «c» не может достичь точки начала медиатора. Развитие влево проходит через несколько характерных точек самого медиатора. И здесь появляются еще две новые. Первая точка на кривой «y2», когда соотношение a/b=1 (окружность этого прямоугольного треугольника еще пересекает медиатор; это можно видеть на самом первом рисунке медиатора, справа от «кита»). 1-ая характерная точка (вершина равнобедренного треугольника) легко вычисляется: x = y = R = (1-Ц 0.5) » 0,293.

А попутно вычисляется и красивое выражение: .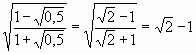

Вторая характерная точка – точка перехода окружности прямоугольного треугольника внутрь медиатора или точка касания наибольшей вписанной в медиатор окружности (см. затонированную окружность на двойном рисунке в начале темы); то есть точка предельного положения треугольника слева на минимальном «с». При расположении вершины треугольника на кривой дальше влево (к концу медиатора) гипотенуза «с» начнет возрастать вправо при все ускоряющемся уменьшении «а/b». Но она никогда не перейдет точку начала медиатора. Гипотенуза внутреннего треугольника как бы заперта в медиаторе, то есть треугольники действительно формируют медиатор по некоторому закону (зависимости). Это особенно явно (последовательно) в следующем случае… В очередной нашей встрече А.П. сообщил, что эта точка – есть начало координат…

Теперь посмотрим случай «y4». Здесь все – более благополучно. Гипотенуза «с» ведет себя однотипно на всем диапазоне x=0ё 1. В точке «0» (в начале медиатора) а/b=1 и с=0. «C», не выходя из медиатора возрастает вместе с отношением а/b. «C» стремится в «1», а «а/b» – к бесконечности. Функция «y4» как бы более однородна, чем «y2». Кривую «y4» можно назвать множеством точек, абсцисса которых равна «а», а ордината равна средне-геометрическому, таким, что отношение «а/b» развивается по некоторой зависимости от «c=a+b» в диапазоне a/b=1ё Ґ (при этом tga =1ё 0).

Мы видели, что медиатор имеет в начале двойной угол 90°. Другие углы образуют другие медиаторы, с общим свойством всего семейства «максимальной эффективности перехода от начала к концу по единой формуле тангенса угла».

Общая формула семейства медиаторов, очевидно, будет иметь вид, где

значение произвольного «p» задает тангенс касательной в начале медиатора.

А ведь это может быть и полуокружность, и отрезок…

А.П. прокомментировал общую формулу медиаторов формулой

соотношения «p» от «x» для произвольных значений «y_max»

и показательной картинкой:

Как видите, на границе множества «оптимальных траекторий» присутствуют окружность и единичный отрезок… Давайте посмотрим на разворачивающуюся картину. Мы имеем кривые равномерного перехода между крайними точками диапазона (единичного отрезка) при разных углах выхода кривых из точки начала и едином угле 90° в точке конца кривых. По условию и по формуле, даже когда выходящий угол стремится к нулю, входящий всегда равен 90°. И при этом, вот ведь что удивительно, как бы кривая не приближалась к оси «X», значение «x_(y=max)» никогда не переходит отметку «2/3». Здесь между этими 90° и «2/3» есть связь…

Еще раз, посмотрим крайние положения динамики. Точка перегиба кривой находится в диапазоне: ¹/₂ ё ²/₃. Когда выходящий и входящий углы равны и равны 90°, тогда точка максимума делит единичный отрезок пополам. Когда выходящий угол равен 0°, «точка максимума» делит отрезок в соотношении 2/3 и 1/3. То есть при встречно направленных двух медиаторах с «p=Ґ », отрезок «точками максимума» делится на 3 равные части; это триада. Триада на отрезках.

Общая же «динамика» такова. Окружность «создает» вторую окружность на том же центре; для двух окружностей, как медиаторов в потенциале, отрезок диаметра делится пополам (в точке центра). Окружности становятся медиаторами; центры двух окружностей расходятся на концы диаметра при одновременном направлении друг на друга своих потенциальных «движений», стремлений (p= 0). Сохраняя взаимное встречное направление, медиаторы меняют «p» (p ® от «0» в «Ґ »), образуя на связывающем отрезке триаду частей. Триада образуется взаимопересеченными двумя отрезками «2/3» или соответствующими окружностями диаметром «2/3». Исходные две совпадающие окружности стали двумя взаимопересеченными.

Можно ли такую «динамику» считать скрытым мета-смыслом наличия у медиатора предельного максимального значения «x_(y=max)=2/3»? Или им может быть что-то иное? Это – ваше решение…

А из «действия» формул также получается то, что как и раньше было, например, «Ґ » и «Ґ ²» – это не одно и то же (см. сноску фантика_7), так и здесь «0» и «Ц 0» – это не одно и то же…

А в какой точке кривых в случаях «y2» и «y4» вершины их треугольников, строящиеся со своего конца медиатора, совпадут? И какие это будут треугольники? То, что это произойдет в середине диапазона «X», очевидно. И совсем не очевидно, что они окажутся равными. Но это в наших случаях так. Мало того, они формируют при этом в центре своими малыми катетами равносторонний треугольник! То есть их окружности проходят через центры друг друга!!

Такие окружности, как известно, формируют красивый цветок на правильном 6-угольнике, на «соте». Значит, и встречно совмещенные медиаторы создадут свой цветок… Это так. Но, чтобы так гармонично, как это представлено на правом рисунке, едва ли можно было знать заранее (можно было только ожидать, предощущать). Каждая линия этого цветка занимает точно равновесное место в композиции всего рисунка. Так могла бы рисовать только рука художника, ведомая ощущением гармонии, равновесия. Чисто же в математике удивительно то, как при развороте би-медиатора по сторонам гексагона совпадают пологие (начальные) половинки кривых во внешней области (образуя во внутренней центральную часть лепестков; а вместе — сферические, выпуклые равносторонние треугольники с углом при вершине 90°); удивительно то, как на внешнем контуре рисунка повторяется уменьшенно образ раскрытых створок (совмещенных зеркальных y2 и y4), делая образ внутренне цельным.

Гармония и математика, алгебра и красота… Сколько еще скрыто в тебе, Золотая пропорция? В каких еще конкретных вещах откроешь ты себя? В каких еще формах проявит себя эта Идея?...

Посмотрим на «сдвоенную» форму медиатора.

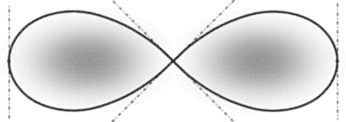
У сдвоенного медиатора есть «двойник» - лемниската Бернулли. Эта кривая имеет 2 центра (фокуса, полюса), как и эллипс. При этом у точек эллипса постоянна сумма расстояний от них до 2-х полюсов; а у лемнискаты постоянно произведение таких радиус-векторов. Если это произведение равно «а²», то и получается лемниската Бернулли. На нижнем рисунке медиаторы находятся внутри лемнискаты.

Увеличить >>>

«Лемниската» означает «бантик, ленточка» на венке триумфатора в Древнем Риме. Этот «бантик» является частным случаем множества овалов Кассини и одним из 5 возможных типов, из которых 2 являются граничными типами между 3-мя остальными. Овалы Кассини меняют свою форму из-за изменения значения произведения радиус-векторов. Пограничные для разных типов овалов имеют таким произведением определенные значения относительно расстояния «а» между фокусами и центром. Лемниската – первая граничная кривая, срединная между эллипсовидными с «талией» и парными отдельными яйцевидными овалами (стремящимися к 2-м окружностям вокруг полюсов); ее r_1Ч r₂=a². Следующим граничным овалом за лемнискатой является овал с горизонтальными участками; его r_1Ч r₂=(Ц 2Ч a)², отметка горизонтального участка y=a, максимальная абсцисса X_max=Ц 3Ч a. Будем называть (при «а», отнесенном к «1») «коэффициентом овала», являющееся средним геометрическим радиус-векторов. Для лемнискаты k=Ц 1, для 2-го граничного овала k=Ц 2.

Посмотрите на это семейство овалов Кассини.

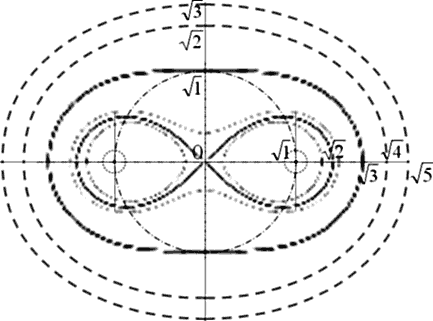
Из рисунка видно, что в овалах Кассини соотношение размеров по ортогональным осям строится «на квадратных корнях». Но это только часть видимого. Взаимосвязь через квадратный корень становится еще убедительнее в следующем выражении: . Здесь «k» – это по определению овалов то самое среднее геометрическое радиус-векторов: .

Три формулировки этого свойства: алгебраическую, геометрическую и «статистическую», - смотри в тексте «О среднем геометрическом».

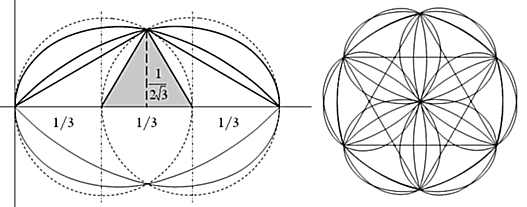
Наш экскурс на этом закончился. А вот с чем он пересечется в нашем «путешествии», увидим дальше. Вы обратили внимание на ряд значений «Х» на верхнем рисунке: 1, Ц 2, Ц 3, Ц 4? С таким же шагом 0,25 по «Y» эта парабола даст далее на оси «Х» отметки Ц 5, Ц 6, и т.д. А в овалах Кассини соотношение «габаритных» X и Y через квадратные корни по порядку? Это напомнило о таком же движении значений «катет-гипотенуза» в «линии качания «С» (см. начало). Интересно увидеть здесь развертку этой линии качания (внизу слева). А заодно посмотреть, как совмещаются развертки 3-х основных линий качания (внизу справа). Формулы значений «катетов-гипотенуз» даны для n=0ё Ґ.

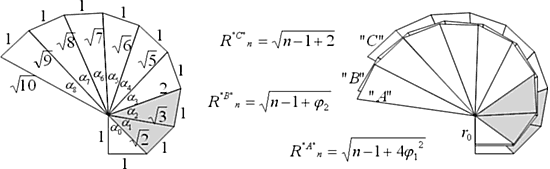
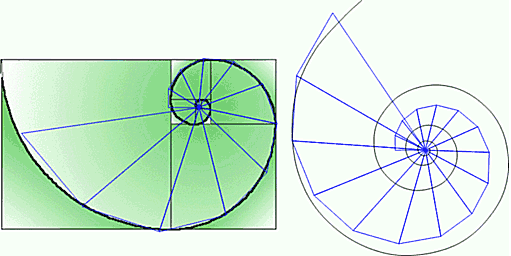
Конечно, такой спиралевидный образ «линий качания» очень нагляден. И он предлагает посмотреть на формирование спиралей с помощью прямых треугольников, соединенных вершинами. Очевидно, что «чистые» логарифмические спирали (монотонно изменяющиеся) могут образовываться таким образом, если все треугольники подобны, то есть имеют одинаковые углы. И первые «кандидаты» на такой опыт — j -спираль и Золотая спираль.

F -треугольник (a » 31,7°) почти точно сформировал j -спираль. Но не совсем убедительно. (Жаль…, но мы еще проверим.) Можно было предположить, что более свернутая Золотая спираль будет формироваться меньшим углом. А каким? Ну, например, (ведь наши золотые объекты отличаются «взаимосвязностью») углом (В₀/2) …

Что получилось – видно ниже.

Чтобы подобрать ключи к этим построениям, нобходим точный расчет. А расчетная схема в принципе не сложна: см.

Формула j -спирали: . Ряд простых преобразований выражения треугольника по теореме Пифагора приводит к простому соотношению: .

В преобразованиях видно, что вид этой формулы универсален для любых спиралей, для любых их оснований. Ранее говорилось, что в любой спирали «множитель полного оборота» равен , и, например, для Золотой спирали он составит: . Тогда соотношение для угла (a) в формообразующем треугольнике Золотой спирали (не путать с треугольниками, образующими систему координат спирали) будет: .

Дальнейшее решение (с помощью «электронной таблицы») дает искомые значения. Для j -спирали формирующим треугольником является прямой треугольник с углом a » 33,084° (tga » 0,65149). Золотую спираль формирует треугольник с углом a » 17,284° (tga » 0,31116).

Увеличить >>>

Так и есть, точный формирующий угол j -спирали чуть больше угла j °. Они настолько близки, что где-то около j -спирали (на формирующем углу ~32°) существует некая 0-спираль, у которой совпадают формирующий угол и угол треугольников в модуле ее осей координат. Это – «центральная спираль». Более сжатые спирали (например, Золотая) в модуле осей имеют б’ольший угол, но их формируют треугольники с меньшим углом. Более развернутые спирали (например, y -спираль) имеют в модуле своих осей меньший угол (y для y -спирали), а их формируют треугольники с б’ольшим углом.

А каким углом, кстати, формируется y -спираль? Общий член ее ряда: . Ее соотношение для формирующего угла: . Из него - угол формирующих треугольников a = 45° !

Угол системы координат y -спирали по катетам: 1: 2.

Формирующий угол y -спирали по катетам: 1: 1.

А как же 0-спираль? Каков единый ее угол? Это нетрудно определить, если вспомнить следующее: ctgb ₀ = N. Здесь b ₀ — угол координатных осей (см. предыдущую сноску), а N – «разворачивающее» основание спирали. Тогда единый угол центральной спирали определится из соотношения: . Он равен a » 32,121° (tga » 0,62781), и k» 1,593…

И мы еще не договорили по Золотой спирали. Во-первых, а что же за спираль получилась на формирующем углу a =(В₀/2)° ? Найти «N», зная «a », не трудно.

Формула синей спирали на правом рисунке в начале этой темы: .

И последнее здесь – этот формирующий угол Золотой спирали: a » 17,284°. Случаен ли он?.. Можно (и нужно) еще пробовать искать… Но здесь есть очередное странное «чуть-чуть». Он всего на ~0,008° больше трети угла «B₀»: .

А помните (?), у нас еще была «круговая спираль», спираль равномерно (с одним приращением, скоростью) нарастающих витков (как дорожки информационного диска). А какой у нее характерный треугольник (с каким центральным углом)? Конечно, он тоже прямоугольный (ведь к любой линии изменяющейся кривизны (радиуса) можно провести прямой треугольник; а нам он и нужен). Предположим, что ее треугольники тоже подобные между собой, и порассуждаем.

Проведите (реально или мысленно) окружность через какую-то точку на круговой спирали. Спираль, раскручиваясь, будет уходить во вне от нее. Через ту же точку можно провести другую круговую спираль (подобную первой, только пропорционально измененную, как в масштабе), которая будет проходить между окружностью и витком 1-ой спирали. Понятно, что 2-ая спираль будет плотнее, то есть на данной площади она будет иметь больше витков. В пределе спираль с бесконечной плотностью витков, проходя через ту точку, станет кругом в пределах проведенной окружности. При этом прямоугольный треугольник с вершиной в центре спирали, проведенный через ту точку, уменьшаясь по центральному к спирали углу, превратится в отрезок радиуса. Мы говорили, что все эти спирали – лишь разный масштаб одной и той же круговой. А при изменении масштаба углы не меняются. Следовательно, изменялся центральный угол одной и той же спирали для витков разной удаленности. А то есть внутренние треугольники круговой спирали – не подобны.

Тогда, какие они? Ведь что-то в них, формирующих равномерную спираль, наверное, должно быть одинаковым?.. Или – нет? Посмотрите на эти рисунки.

Логарифмическая спираль, имея равномерное ускорение разворачивания, описывает и вписывает подобные прямоугольники. Круговая спираль, имея постоянную, равномерную скорость разворачивания, описывает и вписывает прямоугольники с одинаковой одной стороной, равной шагу спирали. У логарифмической спирали подобны и треугольники… А у круговой что будет? – треугольники с одинаковым катетом «а», противоположным центральному углу?... Так ведь это – ситуация «качающихся треугольников» на одном катете! То есть круговая спираль образуется системой треугольников из одной какой-то линии качания «катет-гипотенуза»?! Круговая спираль – частный случай спиралей на основе углов линий качания «катет-гипотенуза»?... Да. Если верно предположение об едином катете «а»…

Что ж, теперь без точной проверки этой спирали и без ее формулы не обойтись. Сама проверка – не сложная. Расстояние между витками – одинаково, а, следовательно, если значения катета «а» (на линии спирали) во вписанных прямоугольных треугольниках через целое количество витков (nґ 360°) одинаковы, то отношение тангенсов их углов будет равно отношению катетов «b» (между центром и витком).

Итак, формула круговой спирали (не имеющей ускорения, а, следовательно, имеющей множитель, вместо степени): . Естественно при одинаковом шаге принять его за «1»: , где a — полный угол до точки от начала спирали. Для «спирального треугольника» запишем: . А для начального из них: .

Из двух формул (для любого r₀) получаем принципиальную зависимость для начального угла круговой спирали: .

Для центрального угла вписанного прямоугольного треугольника через 360° от начала спирали (после 1-го витка) получаем: .

Теперь мы всё можем проверить…

Получилось: a ₀ = 17,5273512…° (tga ₀ » 0,3158237), a ₁ » 9,02466° (tga ₁ » 0,1588258).

Значит. Два треугольника круговой спирали через 1 оборот витка не имеют одинакового основания «а»: а₀ » 0,3158 и а₁ » 0,3177. За один виток катет «а» всего в ~1,006, но все же увеличился.

Так значит, круговая спираль не формируется треугольниками, принадлежащими одной линии углов качания «катет-гипотенуза»… Но вот во время уточнения и перепроверки верхних расчетов был найден очень близкий угол a » 17,55°. Его тангенс равен . - это тангенс угла C₉… Более того, он ровно в 2 раза больше ; то есть через 30 треугольников. Потом кратное уменьшение тангенсов будет через 50 треугольников , через 70 , и так далее. Совершенно красиво… Вопрос только в том, как близко 360° равняется сумма углов этих 30 (от C₉ до C₃₉ включительно), потом 50, 70 и так далее треугольников.

Да и вообще тогда, насколько близко проходят эти спирали – круговая спираль и спирали, образованные углами разных линий качания прямоугольных треугольников на одном катете?.. В самом общем случае для линий углов здесь действует такая пара условий:

и ,

где a ₀₀ – угол «линейки», с которого начинается ее спираль,

a _i – угол «линейки», отсчет которого ведется от a ₀₀.

Для сравнения по 1-му витку (n=2) получаем из этих уравнений: 3 = iЧ tg^2a ₀₀. Целочисленных вариантов получения «3» в произведении достаточно. Но для сравнения с круговой спиралью нас интересует вариант, где a ₀₀ наиболее близок начальному a ₀ круговой спирали. Это – .

В таблице представлены результаты вычислений.

Для полноты коллекции – несколько «точных несерьезностей». Близко к линии углов 4-ой строки таблицы находятся другие «интересные соотношения». Четвертый Х₀ » 72,6°. А tg72,34…° = p. Четвертый Х₁₀ » 17,47°. А tg17,44…° = 0,1p (его Х₀ » 70,02°). Интересно также увидеть (почувствовать) здесь эту близость «хорошего» угла 72°. При Х_0» 72° сумма углов 30-ти треугольников 1-го витка составляет почти 360° (~359,94°).

Мы рассмотрели спирали на участке 1-го витка. И на последующих участках характер поведения этих спиралей не должен меняться. Все «линии качания» формируют спирали очень, очень близко круговой. Начало круговой спирали соответствует углам a ₁₀ линий качания (и углу «С₉» линии и ее спирали, самой близкой к круговой). Интересно то, что прямоугольные треугольники с углами «линеек качания» a _{0ё a 9} как бы дополняют начало круговой спирали. (Сами же линейки углов после a ₀ уходят в мнимую область; в частности одно С_-1 = 90°, а треугольник «-1» становится исходным боковым катетом.)

Таблица отражает «совместный старт» всего множества спиралей и результаты их «финиша» после 1-го витка (пересечения оси X). Как видите, человек на глаз практически не может отличить эти «результаты». Створ, в котором финишируют все спирали, составляет всего 0,05 от шага круговой спирали (хотя разность по сумме углов «отпущенного равного количества треугольников» составляет до ~8°).

Надо еще сказать, что пересечение оси «Х» спиралями «линий качания» определялось катетом «а» треугольника, а не кривым участком между концами этого катета. Возникает вопрос: а не пройдет ли кривая спирали «С» через отметку «2»? Гипотенуза последнего «29-го» треугольника заходит за «ОХ» на угол ~0,874°. Ее длина – «2»! Кривая спирали (не окружности), проходя через эту точку, не может пройти через х=2. Кстати на том же углу расстояние до 2-го витка круговой спирали составит R» 2,0024.

Уточним еще. В таблице у круговой спирали значение «9,024665» не является углом a ₃₀ ее системы прямоугольных треугольников. Прилежащий катет этого угла проходит по оси «Х», завершая полный 1-ый виток (е ° =360°). Что нам и было важно для анализа подобия треугольников спирали. А на самом деле, как выстраиваются треугольники круговой спирали? По аналогии со строем треугольников качания «катет-гипотенуза» приведем данные для последовательности треугольников круговой спирали. Итак, a ₀₀ » 17,5273512°, a ₂₉ » 9,119508°, К_«а» » 1,006 (k_ср. » 1,0002), е (a _{00ё a 29}) » 361,474338°; гипотенуза треугольника «a ₂₉» равна ~2,0041, а ось «Х» будет пересечена катетом а₂₉ на отметке b₂ » 1,9965. Смотрите, как на втором витке действительно близко (~0,001 от шага спирали) проходят катеты «а» треугольников круговой спирали и спирали «качающихся треугольников».

На нижнем правом рисунке представлено движение спирали линии углов «С». Надо лишь привести последние данные этой спирали. Начальные катеты от b₉=1 (шаг спирали). Угол наклона начального катета «b₀» к оси «Y» составляет ~28,2571°. Катет «а» второго треугольника (a _1» 35,2644°) пересекает ось «X» на расстоянии от центра ~0,467. То есть как раз меньше «0,5» условной круговой спирали. На левом рисунке показан результат «старта» всего диапазона спиралей «качающихся треугольников» в лице их крайних линий от начала круговой спирали назад, то есть с одной отметки «1» на оси «Х». Не правда ли, наглядно… А цифры второй крайней спирали (черной) таковы: угол наклона начального катета «b₀» к оси «Y» составляет ~10,7087°, катет «а» второго треугольника (a _1» 35,2644°) пересекает ось «X» на расстоянии от центра ~0,516 (заходя за ось на угол ~0,9731°). И на среднем рисунке показан «старт» крайних в диапазоне спиралей «качающихся треугольников» с одной линии и при одинаковом «а». При этом шаг «черной» спирали составит ~0.87 от шага «синей».

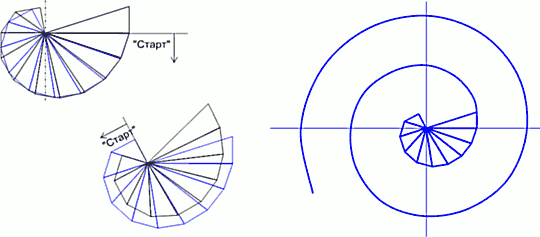
Если мы все множество спиралей «качающихся треугольников» и круговую спираль выставим на «старт» раскручивания на одну отметку, например, в начале второго витка круговой спирали (уж не говоря о 3-ем или последующих витках), то различия между ними станут вообще ускользающе незаметны. На один старт 2-го витка все линии углов будут выставлены с прилежащим катетом b=2 и с углом, наиболее близким к углу системы треугольников круговой спирали на этой же отметке. Мы теперь знаем, что весь диапазон линий углов уложится в углы С_39ё С₄₀ и в соответственно катеты «а»» 0,316ё 0,312 от шага круговой спирали (К-спирали). Но в этот раз все углы будут меньше К₃₀ (на 1-ом витке С₀₉ и Х₀₉ от углов Х₀ » 81° ё 90° были больше К_{00є a 00}). И в этом смысле старт на втором витке К-спирали наиболее показательный (как вперед, так и назад).

Не отличишь: что круговая спираль – что спираль «С» (и другие ее сестры)? Тогда возникает вопрос: кто из них и чей – «частный случай»?

Назовем все множество спиралей «качающихся треугольников» С-спиралями. У треугольников С-спиралей катеты «а» равны, их k=1. А как у К-спирали? Если бы отношение «k» между соседними «а» было постоянно, то увеличение «а» шло бы с множителем «kⁿ». Именно так происходит в логарифмической спирали, у подобных треугольников которой одинаковы углы и их тангенсы, и у которой k = a_i/a_i+1 = cosa. А у К-спирали отношение k = a_i+1/a_i, равное в начале ~1,00067, уменьшается с ее разворачиванием, и достигает в начале 2-го витка ~1,000055 со средним значением ~1,0002. Точно также уменьшается и разность между «а» от ~0,0002 до ~0,00002 (от шага спирали). Мало того, и эти «уменьшения» тоже уменьшаются на следующем уровне сравнения между собой.

Коэффициент «k₁» (уменьшения «k») составляет в начале 1-го витка К-спирали ~1,0001, и в конце ~1,000003 со средним геометрическим значением ~1,00002. Зависимость этого изменения аналогична изменению предыдущего «k», но с основанием на порядок меньшим. И так далее. До предела отношений «k_i» в i-уровне, стремящемся к «1». Такими треугольниками строится К-спираль; самая простая на вид, а на самом деле – вся «на пределе».

Подведем итоги. При таком маленьком начальном основании показательная функция «k^x» имеет очень пологий характер. А в случае уменьшающегося «k» она еще более уполаживается по мере увеличения аргумента «х». Зависимость увеличения «а» треугольников К-спирали получается нелинейной, но чем дальше, тем более близкой к прямопропорциональной по k=1. «k» стремится к «1», все замедляясь в этом «стремлении». У К-спирали «k» не достигает в пределе «1» и потому она уходит в бесконечность.

По другому у С-спиралей. Они стремятся завершиться окружностью. По мере разворачивания все С-спирали будут все более сближаться, все более и более сливаться в одну. Треугольники С-спиралей, имеющие одинаковый «а», стремятся в бесконечности к отрезку радиуса, и спираль сходится в окружность.

С-спираль и К-спираль – самостоятельные виды спиралей. При всей их внешней схожести у них различная сущность, различная природа.

И кстати. Эти круговые спирали (К-спирали) и есть спирали Архимеда. К великому сожалению не встречаются сейчас правдивые иллюстрации, где бы она изображалась именно так – как нарезающая на лучах шкалу равных величин, арифметическую шкалу-зависимость. Везде ей дается одно определение: архимедову спираль рисует точка, движущаяся равномерно по лучу, вращающемуся равномерно. Понятно, что луч делает оборот за одно и то же время, и за это время, за каждый оборот точка проходит по лучу одно и то же расстояние. Но почему тогда рисуют архимедову спираль неравномерной, и делают разные заключения, наподобие какой-то ее несходимости при убывании, что просто не имеет к ней отношения. Просто – неаккуратность…

Или – поглощение смысла тем «физическим определением». Ведь на самом деле, можно начать движение точки прямо от центра, от «0» на луче. С первым моментом равномерного движения она начинает строить равнее расстояния между витками. Но! Ее системный смысл, ее геометрия (в том числе интерпретация на квадро-плоскости) заставляют говорить, что она не должна подходить к центру ближе, чем расстояние между витками. Центральная область – не ее область, это область других отношений (что проявляется и в формуле, в требовании ее неизменности для одной спирали, ведь «k» не может быть меньше «1»). Движение точки должно начинаться не от центра, а от «межвиткового расстояния». Рисуя от центра, иллюстраторы невольно «ускоряются» и рисуют подобие логарифмической спирали.

Мы говорили раньше о показательности 2-го витка для сравнения К-спирали и С-спиралей. Точнее сказать – показательны для С-спирали события 1-го витка К-спирали (или 2-го С-спирали). С-спирали на своем 1-м витке выравниваются по треугольникам и приближаются к К-спирали по параметрам. Именно на 1-ом витке С-спиралей их линии углов по качанию «катет-гипотенуза» теряют свои особенности. Кстати, мы и раньше видели, что только первые 6-7 углов в линиях углов являются характерными.

Интересно, конечно, было бы найти некую общую формулу С-спиралей. Да мы и так уже далеко зашли в своих поисках. Ушли в сторону из нашего Сада. Может быть, кто-то пройдет и дальше… Но вот с самого начала этого поиска меня сопровождал образ вывода космического корабля на орбиту планеты. Я нарисовал его траекторию с помощью С-спирали «a ₀=45° ».

Заметьте также, что на энерго-диаграммах А.П. Саврухина "катет"-вектор, исходящий из начала координат, исходной частицы является "гипотенузой"-вектором полной энергии результирующей частицы. И дальше при много-частичном распаде эта последовательная схема чередования "катет-гипотенуза" (исходящих из центра) образует какую-то С-спираль (на каком-то a ₀)…

Мы, кажется, подходим к концу этой темы. Еще раз, что общего и различного в 3-х видах спиралей? Круговая спираль разворачивается равномерно, логарифмическая (окружная) равномерно ускоряет свое разворачивание, а С-спираль замедляется, переходя в пределе в окружность. С-спираль и К-спираль имеют начало. К-спираль и логарифмическая не имеют конца.

Главное, что их объединяет, они формируются одним общим, их все сроят прямоугольные треугольники. Их и назвать можно по этому родовому признаку: спираль «одного катета», спираль «нелинейных катетов» и спираль «подобных катетов». Можно им написать и общую формулу: a_i = a_0Ч k_i, где для спиралей «одного катета» k_i = koЧ 1

для спиралей «подобных катетов» k_i = (seca)ⁱ

а для спирали «нелинейных катетов» зависимость мне неизвестна…

Кстати, можно назвать коэффициенты k₀=seca =Ц (1+tga) известных спиралей:

У j -спирали k₀ = t » 1,1756, у золотой спирали k₀ » 1,0473.

Всё вроде бы ясно. Но при таком положении возникает тот самый простой детский вопрос: а почему именно треугольники формируют все эти спирали? Причем в самых разных комплексах.

Вернемся к началу текущего разговора о спиралях и вспомним рисунки начала текста, где впервые мы встретились со спиралями: тогда именно «качающиеся прямоугольные треугольники» образовали модуль осей координат Золотой спирали.

А вспомните схему прямоугольного модуля логарифмической спирали. Логарифмические спирали здесь строятся, как говорили прямоугольными треугольниками по метафоре «поворот катет-катет». И ее формирующие треугольники остаются всегда подобными.

Кстати, первый треугольник круговой спирали со значениями a₁=1, b₁=1,5 и h₁=1,25 имеет угол в вершине ~88,9°, а при основании углы ~51,3° и ~39,8°. Раскручиваясь в бесконечность К-спираль стремит свои такие треугольники к прямоугольному с углами 45°. Естественно, такие ее треугольники не образуют оси координат.

Для полноты надо вспомнить, что спираль можно представить на перпендикулярных (ортогональных) осях двумя волнистыми линиями с изменяющейся амплитудой. Так же, как мы можем представить некой неправильной спиралью волнистую линию приближения к значению Золотой пропорции величин отношения соседних членов ряда Фибоначчи.

А посмотрите этот рисунок Валерия Гагина.

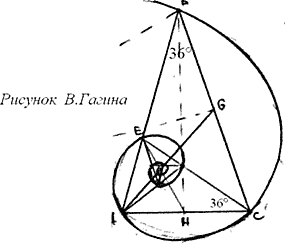
На нем j -спираль формируется системой равнобедренных треугольников с углом 2b =36°. Этот угол составляет часть угла при основании более большого треугольника, и вся система их как бы вращается вокруг центра спирали, задавая своими вершинами саму спираль. А интересно, какие 2b -треугольники формируют другие известные спирали? Во всяком случае, их диапазон распространяется от 2b <60°. При 2b =60° получается окружность, описанная вокруг этого равностороннего треугольника.

Так почему именно все эти треугольники формируют все эти спирали? Мне кажется, потому же, что и у А.П. Саврухина, и у И.Ш. Шевелева. Спирали – это может быть самый лаконичный, самый эстетичный, самый гармоничный математический образ. В ней содержится завораживающий смысл бесконечного развития (…), бесконечного раскрытия на одних и тех же простых правилах и составляющих. Именно векторный треугольник, прямоугольный треугольник универсально представляет элементарное развитие, формирование. «90° » создают некую «единицу», выражающую свой потенциал формообразования целостно и полно именно в тре-угольниках…

И надо вынести отсюда главное убеждение о родовой связанности треугольника и логарифмической (окружной) спирали, триады и логарифмической спирали.

Ну что ж, пойдем дальше?

Давайте посмотрим на отношения «3-х» через такой рисунок.

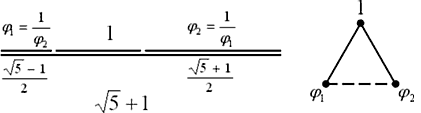
Глядя на нижние на рисунке выражения этих величин, возникают интересные аллюзии по возможным их отношениям. Но что бесспорно, j ₁ и j ₂, как полностью противоположные величины, обретают общую гармонию через «1». Каждая из них имеет с «1» золотые отношения. И каждая получается через отношения других 2-х. Посмотрите действия между 2-мя элементами в «треугольнике», приводящие к 3-му… И это – разные действия формирования каждой сущности, кроме действия, идущего от «1» и действия между j ₁ и j ₂… Так получается самодостаточная устойчивая триада. Взаимопереходящая триада, то есть действующая, функциональная.

Безусловно, это соотношение говорит об отношениях 3-х «сущностей»…

И вспомнился один из разговоров с А.П. Саврухиным.

- Вы выделяете Два Начала (Дао и Дэ). Как Вы "соединяете" их с "Троицей"?

- Из одного — ничего. Из двух — все, это и есть минимум. Эти два порождаются одним, поэтому их три. ЕДИНЫ и НЕСЛИЯННЫ! В моей физике единое поле имеет две ортогональные компоненты. По традиции: Дао — всеобщий абстрактный принцип, дэ — его манифестация. Дао как истинное первоначало проявляется как Дао-первоисточник и как Дэ-манифестация. А в основе жизни: Дао — закон сохранения жизни, естественная основа, и дэ — его проявление, нравственность как основа культуры. Теоретическая физика в тупике из-за пренебрежения Дао и дэ; поэтому неизбежно обращение к истокам.

По учению мыслителей древнего Востока, все сущее создается из двух начал. Первое ничем не проявляется, не постигается сотворенным из него же и напоминает физический вакуум. Второе происходит из первого, является творцом вещей и служит прототипом полей и частиц.

«Природный источник ничем не выделяется. Первопричиное не имеет побуждения к деятельности, поэтому облик его скрыт. (это Дао – А.П.).

Кормилица всех существ богата формами. Повседневное имеет побуждение к деятельности, поэтому облик его обозрим. (это Дэ – А.П.).

Они вместе выводят, но разнятся приметами. Вместе называют их первоначалами: творческое начало природы, да еще исток, посредствующий всеобщего созидателя» (Лао-Цзы)

Это первопричинное даосы именуют Дао, что означает высший абсолют, основной закон, вездесущее начало, всеобщий закон движения и изменения мира, источник всех явлений, из которого все исходит и к которому все возвращается. Единственное, вечное, неизменное, но способно выступать в разнообразных формах и порождать все сущее. Неограниченная субстанция, не постигаемая органами чувств, вне времени и пространства.

Так говорил даос и физик. А для меня во всем пути оставался вопрос отношений «дуады» и «триады». Он прорывался через разное. С самого начала мы видели роль триад в формировании, мы видели в схемах ВО-трансквадрата «Троицы», формирующие мир. И их было Две…

Я знаю все стрелы, которые будут пущены сейчас. Но я ведь не настаиваю... И я думаю, образы и смыслы математики, как никакие, связаны с основами бытия, с онтологией.

Попробуем все же дальше подумать о смыслах двух триад (поиски и осмысление символов не закончены!…)

Триада отношений: чтобы Они оставались Целым, Сущностью становится и их Связь. Так между 2-мя любящими людьми сущностью (ценностью) становится их любовь…

Триада формирования: чтобы формируемое было целым и устойчиво (гармонично) развивалось, его пропорции (части, элементы) должны соотноситься по Золотому правилу…

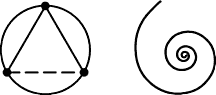
Представим эти особенности в таблице. И как говорится – без комментариев.

Увеличить >>>

А что это за красивый образ здесь появился? Это образ «Золотого пространства» или «Золотой плоскости» из «Золотых спиралей». Центры ее вихрей располагаются на осях под углом «В₁=arctg(Ц j ₁)» к вертикали (или «В₀=arctg(Ц j ₂)» к горизонтали). Он возник из развития геометрии плоскости, в которой под этими углами располагаются ортогональные оси Золотой спирали, постоянно порождающей на разных отрезках золотые пропорции. Новые вихри возникали на пересечении 2-х линий других вихрей, а новые «центры пространства» – на пересечении 4-х.

И я позволил себе здесь немного пофантазировать, представив энерго-диаграммы распадов частиц Саврухина как бы «репрезентативными» для процессов в пространстве. Здесь интересен сам подход и возможные выводы.

По А.П.Саврухину «энергетика элементарных частиц может быть описана своеобразным набором формул, непременными элементами которых являются полуцелые степени числа Фидия «Ф». Если распад пиона (по А.П.Саврухину, давший ему «ключ») окажется в чем-то определяющим (выдающимся) для других распадов, то можно ли предполагать, что по каким-т связям основная структура пространства с-троит-ся по «Золотой спирали». Можно ли предположить, что структура пространства так или иначе связана с Золотой пропорцией?…

Если бы физика элементарных частиц была связана с геометрией, то есть реакции распада были связаны с местом (точками) распада и «биографией» нахождения в предыдущих точках пространства, то это значило, что пространство моделируется происходящими событиями или/и моделирует цепочку событий по некоторому начальному звену. (Вопрос – что есть начальное звено…) Во всяком случае, тогда возникает связь между состоянием пространства и происходящими событиями, то есть субъекты событий влияют на пространство.

И хочется в заключение подумать о терминах «правая спираль» и «левая спираль». Человечество использует большей частью так называемые «правые» спирали. В правых 3-х мерных спиралях (винтах, шурупах; кстати, их действительно удобнее вворачивать правой рукой именно такими) при движении по часовой стрелке точка уходит от наблюдателя (при просмотре с любого конца). Мы говорили, что раковины тоже строятся витками так называемой «правой спирали»; если смотреть со стороны их вершины, то, двигаясь по часовой стрелке, будем по расширяющимся виткам уходить от вершины. По аналогии и плоская спираль считается «правой», если, двигаясь по часовой стрелке, двигаешься от центра. Но мы до сих пор не сказали, где находится «наблюдатель» по отношению спирали. Если смотреть изнутри раковины, то прежнее движение будет уже «против часовой стрелки». Если смотреть на плоскую правую спираль не извне, а с другой стороны, то она тоже будет «левой». Получается, что вопрос «правизны-левизны» спирали – это вопрос, если хотите, онтологический – откуда смотреть: снаружи или изнутри, кем является наблюдатель: «посторонним» или «хозяином», и чья тогда точка зрения правильная?.. Как Вы считаете? Я думаю правильная – точка зрения нахождения внутри природы.

Но это просто общие «воображения»…

[Обсуждение на форуме «Наука»]