|
|
Алферов С.А.
Классическое определение:
Золотая пропорция — такая пропорция (деление) отрезка, что отношение большей части к меньшей равно отношению всего отрезка к большей.
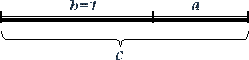
В последовательности отрезков «a-b-c» средним по длине отрезком является «b». Отсюда понятен смысл одного из старинных определений золотого сечения, как деления отрезка «на средний и крайний» (а не на два конкретных: больший и меньший).
Решение системы уравнений, составленной из определения для c: c2 — c — 1 = 0, — дает одно из значений Золотой пропорции: c1,2 = 0,5 ± Ц 1,25.
Напомним алгебраические выражения Золотой пропорции для обоих ее значений:
|
|
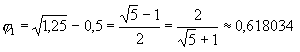
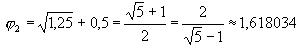
И два основополагающих свойства: 
Существуют также 2 бесконечных выражения значения Золотой пропорции, состоящие из «1». Причем первое – более полное выражение, потому что задает j2 и j1.
|
|
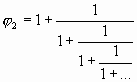
И как отношение соседних членов ряда Фибоначчи образует в бесконечности Золотую пропорцию, а в свою очередь ряд степенных значений над Золотой пропорцией образует ряд Фибоначчи, точно также эти выражения Золотой пропорции через «бесконечные единицы» имеют обратное дополнение: j12 + j13 + j14 + … + j1n = 1 (и конечно, добавив j11, получим j2).
Кстати, первое выражение – более полное, потому что задает j2 и j1.
А вы не хотели заглянуть в бесконечную глубину этих выражений? Что мерцает там – в бесконечном далеке этих формул?.. У первой – «1/2», а у второй – «Ц 2»…
Посмотрите, какая последовательность значений знаменателя получается в полной формуле?.. Не правда ли, интересно?
Переворачивая «числитель-знаменатель» и прибавляя «1», получаем ряд Фибоначчи. Кстати, таким образом можно получать ряд с любым началом. Здесь «1» выполняет задачу «сумматора» знаменателя к числителю. Интересная игра в перевертыши, в которой каждый раз, чтобы навести порядок, появляется «1».
А второе выражение есть следствие формулы 
. Или словами: бесконечное извлечение квадратного корня после прибавления «1» к предыдущему извлечению при исходном подрадикальном значении «2» приводит на «последнем» извлечении к j22. То есть «1» своим бесконечным суммированием превращает
И что же за странная загадка присутствует в выражении «Золотой пропорции»: 
? Именно четверть целого, как некая «элементарная функциональная часть» добавляется к «1» и участвует отдельно в точном выражении для j1/j2 …
Картина какой развертки застыла здесь? Какие здесь представлены структурные отношения? Как, то есть благодаря каким отношениям, эта бесконечная формула 
обрела конечность в верхнем выражении? Как бесконечная внутренняя углубленность реализовалась в открытое во вне и лаконичное выражение? Почему и как повторение самого себя раскрылось выделением «четвертинки» с формированием новой целостной устойчивости, открытой творчеству? Как одно выражение вышло из себя и обрело новое качество?… Странные вопросы для математики?
Все графические построения отрезков Золотой пропорции делались, как помните, через плоскостную фигуру – y -треугольник (a:b=0,5), который и заключен в первом радикале общего конечного выражения… Мы видели также, что именно радикалы из j1 и j2 создают гармонию треугольника «золотой спирали» (a:b=Цj1), то есть создают гармоничные плоскостные отношения. А взятие то радикала как раз и превращает «плоскость» в «линию»…
Тогда можно попробовать трактовать в единицах плоскости: «1/4» — это одна «четвертинка» плоскости, а под первым радикалом – 5 «четвертинок». Да этому есть и точная предметная иллюстрация 
(комментарии этим квадратикам, наверное, не нужны). То есть мы берем радикал из некой «трансцендентной сущности» — плоскости, ставшей (на какое-то время) избыточной на ¼ себя, на единичный элемент себя. И одновременно прибавляем (или отнимаем) радикал из этой самой избыточности (этой четвертинки)… И прежде чем они приходят в отношения, они как бы сближаются, гармонизируются радикалами из себя… Вопросы, вопросы, троеточия, волнение тайны.
Эти странные рассуждения, по крайней мере, выявляют (кстати, не первый раз) более фундаментальным (первым) именно j1, как «возвращающий к 1».
И снова, возвращаясь к этим двум формулам: «линейной» и «плоскостной». Переход между ними – это перевод из гармонии линейных отрезков в плоскостную гармонию,… переход к конечному выражению через гармонию 2-х мерных пространств… Но почему мы, 3-х мерные существа, существа, живущие в 3-х мерном пространстве, берем в качестве «онтологического основания» закономерности 2-х мерного пространства? Может быть дело в том, каким пространством мы полностью управляем. Находясь внутри 3-х мерности, мы не контролируем это пространство. Мы не видим, что за углом. Чтобы его контролировать, надо быть 4-х мерным. Невозможно контролировать свой уровень присутствия. И мы полностью контролируем события плоскости. Находясь вне ее. Поэтому ее закономерности являются нашими закономерностями?!..
Мы воспринимаем гармонию в плоскости. И рассуждаем – плоско… Находясь в 3-х мерном пространстве, мы фатально не владеем его гармонией. Так получается? Мы видим гармонию кругов, но не знаем гармонии сфер, и тем более не руководствуемся этой гармонией. Телесная природа – это природа 3-х мерного пространства. Чтобы попробовать воспринять другую гармонию, человек должен подниматься над телом, над эго… Органично ли это ему, является ли это частью его природы?… Вопрос этот может появляться в разной форме, и каждый отвечает на него сам.
И все-таки интересно, есть ли математические параметры гармонии 3-х мерного пространства, как «Золотая пропорция» в 2-х мерном?
А помните исходное уравнение, из которого мы посчитали в самом начале значение Золотой пропорции? X2 = X + 1. То есть уже в нем задаются отношения площади и линий. Это равенство (уравнение гармонии) звучит так: «исходная площадь, равная сумме сторон площадей: исходной и единичной»…
А ведь отсюда по аналогии можно сделать шаг в сторону «объема»: X3 = X2 + 1 …
И в сторону «представителя гармонии в 3-х измерениях»?..
Неужели здесь ответы на предыдущие вопросы? Аналогии замечательны (первостепенны) в юморе. Аналогии полезны для пояснения своего понимания. А здесь?
Это выражение было определено вместе с другими аналогичными выражениями, объединенными обобщающей формулой еще Алексеем Петровичем Стаховым (по отдельным источниках — вместе с Витенько И.В.). Ими была введена исходная обобщающая формула пропорций деления отрезка (c) на 2 части: 
Помните, когда в начале мы получали аналогично Золотую пропорцию (x=j2) там не было степени (или она равнялась «1»). И из этого соотношения было получено для любых вариантов деления отрезка следующее интересное выражение: xp+1 = xp + 1.
Частным случаем которого и являются верхние 2 уравнения: «плоскостное» и «объемное»...
Параметр «p» задает ряд возможных делений исходного отрезка по некоторому «однотипному» правилу. А уравнение при разных значениях «p» дает разные решения (корни), дает ряд значений «гармоничных делений» отрезка. Стахов А.П. принял для значений этого ряда идентификатор «tp». Вот первые эти значения: t0=2, t1=j2, t2=1,465.., и т.д. к «1».
То есть термином «Обобщенные золотые сечения» на самом деле утверждается равнозначность этих пропорций?.. Перед лицом общей формулы, это так. Но такая «ординарность» еще более вызывает сомнение, что то «кубическое уравнение», являющееся частным случаем уравнения Стахова, даст значение гармонии в 3-х измерениях. И опять тогда – равнозначны ли по значению (смыслу) эти значения одному из них – Золотой пропорции?!
Обобщенное выражение (через параметры) самой Золотой пропорции можно найти. Сюда выводит формула Золотой пропорции в смыслах плоскостных элементов. Можно вспомнить ее «всегдашнюю» модификацию: 
.
И тогда можно представить обобщенную формулу – так: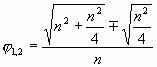 
или так: 
,
где n2 – исходная площадь
m2 – «приращенная площадь»
Здесь n=2m. То есть пары значений «n»-«m» образуют для получения j2/j1 ряд согласованных значений, равных степени «2-ки»: 1 — 0,5, 2 – 1, 4 – 2, 8 – 4, 16 — 8 и т.д. Интересно, что формула работает и при дробных значениях ряда. И вывод. В формуле Золотой пропорции принципиальны: отношения именно квадратов внутренних значений и кратность их «4-ке».
А вот еще интересная формула. 
Она приводит к предыдущей формуле при m=1…
Это формула Татаренко А.А. Он приводит ряд значений Tm и придает этим значениям космогонические и прикладные смыслы.
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| Tm1 | 1 | j2 |
|
|
j23 |
|
|
… |
| Tm2 | 2 | j1 |
|
|
j13 |
|
|
… |
При этом, как принцип гармонии выделяется T2 =Ц 2 ± 1.
Задержимся, посмотрим, что здесь сочетается.
Первое, хочется внимательнее посмотреть на последние две формулы. Формулу Татаренко можно также выразить через «m» и «n» (с подбором пар). И формула будет точно такая же, как обобщенная для j2/j1 (только слагаемые под радикалом меняются местами). То есть вариантов формулы Татаренко много. То есть формула Татаренко может работать при разных парах «n»-«m». (И при этом с разным шагом для значений Tm.) Получается, что в этой формуле: n – оператор изменений, а m – градационный шаг, элементарный шаг…
Но тогда есть 2 вопроса: какой вид у самой простой (имеющей при этом самый большой шаг в значениях «T» при целых значениях «m», и одинаковы ли возможные пары «n»-«m» для каждого значения «Tm»?
Пойдем с последнего вопроса. Так вот, для всех значений «Tm» варианты формул будут правильными при соотношении n=2m (как и для Золотой пропорции). А вот для «T2 =Ц 2 ± 1» варианты формул будут правильны при соотношении n=m. И тогда вопрос – что здесь «родовое»?
А вот самый простой вариант формулы (при m=2k): 
.
Для всех значений «Tm» (ряда Татаренко) шаг «k» должен быть 0,5. Как всегда при значении внутреннего параметра, равном его шагу, получается формула Золотой пропорции.
И интересно подрадикальное значение! Вот где нам встретилось «k2+1», удивившее в свое время странными свойствами. Но об этом ниже.
И все же. Что первично? Золотая пропорция или 2 обобщающих подхода: Стахова и Татаренко? Мне представляется, что первична Золотая пропорция сама по себе.
Золотая пропорция – не простой частный случай неких обобщающих выражений. Ни один другой член обобщающих рядов не равнозначен Золотой пропорции. Обобщающие выражения – это продвижение принципа Золотой пропорции с введением некоторого неединичного параметра. Ведь, что интересно, Золотая пропорция всегда имеет i=1: T1=j2, t1=j2
. Остальные значения – это может быть игра ума. «Tm» и «tp» — могут быть танцами вокруг Золотой пропорции.
А если эти другие значения (пропорции) находятся в природе и космосе?.. Я бы посмотрел на это очень внимательно. И это было бы очень интересно…
Пока же одно обобщение представляется формальной модификацией деления отрезка «в среднем и крайнем отношении»; механистичной модификацией, искажающей саму идею этого «высокого отношения», искажающей исходный принцип самой Золотой пропорции. Если остальные члены такого ряда не обладают исходным свойством Золотой пропорции, а лишь ее аналогией, то может быть, они обладают другими замечательными свойствами Золотой пропорции? А если нет – то почему они в «одном ряду»? Только потому, что красиво смотрится такое обобщение, многообещающе… Хотя. Надо опять же смотреть практические факты такого ряда.
Другое обобщение является модификацией самой формулы значения Золотой пропорции через введение в нее одного обобщающего параметра. Это не единственно возможная такая модификация, но очень органичная…
Вообще представляется продуктивным такой поиск, в котором ищется повторение свойств Золотой пропорции в других комбинациях параметров. В котором исходным является сохранение свойств, а не искажение (или потеря их) в ряду значений, просто объединенных некой общей формулой. Должно быть единство некоего смысла, сохранение смысла. А не просто единство в каком-то обобщающем выражении…
Что ж. Раз заговорили об этом маршруте, так и попробуем его сделать. Исходное, фундаментальное двойное свойство Золотой пропорции обведено самой первой рамочкой в самом начале путешествия: k2*k1 = 1, k2 – k1 = 1. То есть нам нужен ряд парных значений, обладающих хотя бы каким-то одним из этих свойств. Понятно, что этот ряд должен иметь формулу.
Возьмем первое свойство. Именно оно оказалось основой соотношения, приведшего затем к замечательным свойствам «k2+1». Эти свойства связаны с парой величин «a=k2+1», которые дают «единичные произведения»: 
Здесь же для этих сомножителей, чтобы не путаться далее, введем обозначения. Для значений предполагаемого обобщающего ряда применим большую букву F. Парные значения – Ф2(k), Ф1(k) (или Ф2,1).
Давайте их запишем ниже в таблице.
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| F2,1 | Ґ, 0 |
|
|
|
|
|
|
|
Сами значения довольно длинны. Весь волнующий момент – а чему равна их разность?
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| F2 — F1 | Ґ | 2/1 | 2/2 | 2/3 | 2/4 | 2/5 | 2/6 | 2/7 |
О-ля-ля! Такая стройность бывает – не у случайных вещей. Это действительно правильная (по сохранению важного свойства) обобщающая формула Золотой пропорции.
И, естественно, напрашивается – построить график значений.
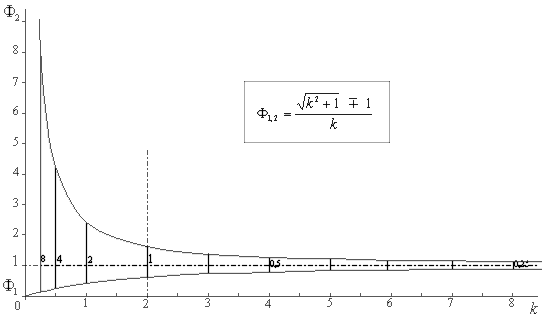
«Выведем область», близкую к «0». Вот таблица значений, меньших «1».
| 1/8 | 1/7 | 1/6 | 1/5 | 1/4 | 1/3 | 1/2 | 1 | k |
|
|
|
|
|
|
|
|
|
F2,1 |
| 16 | 14 | 12 | 10 | 8 | 6 | 4 | 2 | F2 — F1 |
И она по особенному интересна.
Представим k<1 так: k=1/n.
Тогда общее выражение станет: 
Смотрите – какие «перевертыши»! Как в «фокусах ВО-прямоугольников»(см. статью «Динамика ВО-прямоугольников»). Это здесь бывает. Здесь – в удивительном мире «вписанности-описанности и Золотых отношений».
И Вы смотрите, как это выражение подобно выражению Татаренко (в простой форме). И числовые значения совпадают. Значит у Александра Анисимовича здесь – не танец. Только выражение – перевернутое… И по какой же тропе тогда на него выход?
Просто из уравнения x2 — mЧ x -1 = 0 ?..
Кроме того, эта «m» то и задает как раз разность (x2-x1).
Тогда «формула Татаренко» — это по смыслу: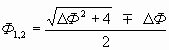 
И из таблицы, и из графика следует свойство D Ф2-1 = f(k) = 2/k. Оно является вторым обобщающим свойством вместе с Ф2*Ф1 = 1. Приведем лишь значения некоторых пар «k-D Ф».
| k | j1 | 2/p | 2j1 | j2 | p | 2j2 |
| D Ф | 2j2 | p | j2 | 2j1 | 2/p | j1 |
Интересно здесь вспомнить, что у p -пирамиды
1
Но это как раз и бессодержательно. Потому что имеет (в очередной раз) просто внешнюю аналогию. Потому что это – формально. На самом деле у пирамид – свои характерные соотношения; и среди них то и появляется Божественная пропорция, задавая гармоничный образ одной из пирамид. Надо быть аккуратным. Адекватность и заключается в мере. Или в том, что всему – свое место.
Первая попытка «размещения» пирамид на графике — пример «привязки» существенного (характерного) признака объекта и тем самым самого объекта не к лучшему (адекватному) ему отношению. Мы предположили сопоставить «h/b» со значением «2/k», которое есть разность (Ф2-Ф1). Но отношение «h/b» само есть некое Ф1, имеющее обратное себе Ф2=b/h. Вот эти значения Ф1 и Ф2 и имеют непосредственное отношение к пирамиде. Ниже мы приведем значения «k» и «a» 5-ти «интересных» пирамид. Нетрудно посчитать, как разность (2/k), так и сами значения Ф2 и Ф1 этих пирамид.
Вообще, в силу того, что все же Божественная пропорция – одна, и, преемствуя нашим предшественникам, было бы правильно называть полученный ряд, имеющий некую обобщенную формулу, не «обобщенными Золотыми пропорциями», а просто «Золотыми коэффициентами», «Золотым рядом», или даже «коэффициентами Золотой пропорции», «рядом Золотой пропорции».
Давайте теперь посмотрим на свойства «k2+1».
Есть два известных в практической математике выражения: 
и 
.
Также, как у похожих по выражению j2 и j1, разность их равна 1. Вы, наверное, заметили, что золотую пропорцию как бы сопровождают две цифры:
Кстати, давайте убедимся в правильности интересного выражения
Возьмем общий случай 
. После переноса знаменателя в правую часть получаем: √a+1=(a-1)Ч (√a+1), что выполняется при a=2!
В принципе, это обычный частный случай в алгебре… Или за ним что-то спряталось?...
Так, если аналогично поделим 
, то будет уже известное нам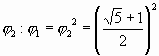 
.
То есть в первом общем выражении с «a» в знаменателе должно быть некоторое k (=1, когда a=2).
Так, и если мы перевернем левую и правую часть (поделим 1 на них), то получим знакомое по виду 
. И тогда в самом общем случае получается: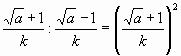
и 
!!
И эти равенства выполняются при определенном соотношении «a» и «k»:
k2 = a – 1 или a = k2 + 1
А это уже интересно. Пройдем по этой тропочке, построим ряд значений a=f(k).
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| a | 1 | 2 | 5 | 10 | 17 | 26 | 37 | 50 | 65 | 82 | 101 | 122 | 145 | 170 | 197 | 226 | 277 | 290 | 325 | 362 |
Конечно, четные и нечетные в «a» чередуются. И сразу виден характерный случай, когда «a» равно простому числу (делящемуся только на себя и на «1»). А, кроме того, многие «a» кратны «2» и «5»... Можно посчитать дальше значения a=k2+1; уточнением выявляющихся закономерностей станет только то, что в самом общем случае вместо одного простого числа окажется произведение двух простых чисел.
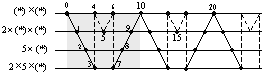
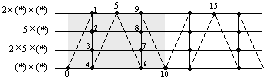
Обозначим простые числа так: (*), и смотрим, что получается:
| Уточним, что в выражениях для k=…0 и k=…1 одно из (*) может быть «1», а если не «1», то оба простых числа — из бывших ранее. И, кроме того, для k=18 будет а=5×5×(*) Обратите внимание, что в этой последова- тельности присутствует определенный ритм. Можно сделать ритмический рисунок ряда. В нашем случае получится даже 2 рисунка, начиная или с а=(*), или с а=2×(*). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
Неплохо бы ввести обозначения двух величин, 
получаемых из каждой пары «k-a»:
Через эти величины можно выразить общие свойства.
Мы помним, что принадлежащие этим выражениям j2=D5 и j1=d5 образовывали между собой характерные зависимости j2Чj1=1 j2 — j1=1. А как в общем случае?
Легко убедиться, что они имеют следующий вид 2
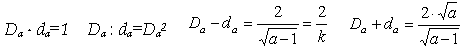
и в частности DҐ — dҐ = 0; DҐ + dҐ = 2
Мы получили общие свойства неких обобщенных «гармоничных» соотношений!
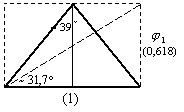
Здесь интересна 3-я формула в своем «пересечении» с «предыдущим». Помните, мы говорили о размещении пирамид на графике? За счет того, что пирамидам можно «сообщить» взаимообратные коффициенты (k1*k2=1), являющиеся соответственно отношениями h/b и b/h пирамиды или tg и ctg диагонального угла «габарита» пирамиды (см. рисунок поперечного сечения «Золотой пирамиды»).
Вычислим «k» и «а» некоторых интересных пирамид. Определим эти пирамиды по их поперечному сечению, то есть проходящему через середины сторон основания.
«Золотая пирамида» — имеет сечение, вписанное в «Золотой прямоугольник», половинный угол при вершине ~39° и длину бокового ребра ~0,94 от стороны основания.
«Пирамида вписано-описанного квадрата» — имеет сечение, вписанное в нижнюю часть относительно горизонтальной оси ВО-окружности, которая проходит через верхние углы квадрата и середину нижней стороны.
«Пирамида золотой спирали» — имеет сечение с половинным углом при вершине ~38,2°, тангенс которого равен Ц j1, и длину бокового ребра ~0,95 от стороны основания; ею является пирамида Хеопса.
«p -пирамида» – пирамида, высота которой равна радиусу окружности с длиной, равной периметру основания пирамиды.
«Пирамида шаров» — имеет половинный угол при вершине ~35,3° и длину бокового ребра равную стороне основания.
| Пирамида | Ф1=h/b | k | a |
| «Золотая пирамида» | j1» 0,618 | 2 | 5 |
| Пирамида ВО-квадрата | 5/8=0,625 | ~2,051 | ~5,208 |
|
Пирамида «Золотой спирали» |
Ц j2/2» 0,6360 |
| |
| p -пирамида | 2/p » 0,6366 |
|
|
| Пирамида шаров | Ц 2/2» 0,707 | 2Ц 2» 2,83 | 9 |
Нам часто встречались также «половинные» выражения, то есть с «2» в знаменателе. Во всяком случае, именно выражения типа 
оказались нам важны.
Вот общий вид соответствующей пары значений: 
и
Нетрудно посчитать, что 
; 
; Bn – bn = 1; Bn + bn = √n
Что связывает их с предыдущими последовательностью и выражениями?
Произведение двух взаимосвязанных чисел последовательностей при n, равном 2 и 5, равно соответственно 0,5 и 1,0. Квадратный корень из них дает рациональное число. Общее выражение такого квадратного корня: 
, откуда 
или 
.
Сравните последнее с: 
Череда «m» с шагом 0,5 дает ряд значений «n»: 1, 2, 5, 10, 17, 26,... Наш ряд!
«Рискнем» утверждать, только при значениях из этого ряда можно извлечь квадратный корень из произведения 
в виде рационального числа. Небольшой «довесок» к достоинствам «k2+1». Общим же для всего выше сказанного является присутствие Золотой пропорции: j2 = D5 = B5; j1= d5 = b5.
Примечания
1)
∞ Ч % = 1 ∞ : % = ∞2 ∞— % = ∞ ∞ + % = ∞
Отнеситесь с юмором, юмором юмориста из некой системы счисления…
Алферов С.А. Обобщенная формула Золотой пропорции // «Академия Тринитаризма», М.,
 |