Когда речь идет о той или иной математической теории (теория чисел, геометрия, алгебра, дифференциальное и интегральное исчисление, теория вероятностей, комбинаторика, дискретная математика и т.д.), под этим всегда понимается строго очерченный круг математических аксиом, постулатов и теорем, то есть некоторых достоверных математических результатов, которые в совокупности и определяют содержание той или иной математической теории и ее приложения.

Существуют различные критерии для оценки результативности той или иной математической теории. Пуанкаре называл изящным математическое построение, позволяющее вывести наибольшее число положений из наименьшого числа посылок. Для Эйнштейна такими критериями являются «внешнее оправдание» (согласие с опытом) и «внутреннее совершенство» (изящество теории отражает ее близость к действительному миру). Наконец, результативность теории оценивают наличием «неожиданных», непредсказуемых результатов.

Рассмотрим, насколько удовлетоворяет этим критериям «Математика Гармонии», основы которой изложены в работах [1-5].

Прежде всего об истории «Математики Гармонии». В своих истоках «Математика Гармонии» восходит к «Началам» Евклида, в частности, к Евклидовой задаче о «делении в крайнем и среднем отношении», сформулированной Евклидом в Книге 2 (Теорема 2.11). В современной науке эта геометрическая задача получила название «золотого сечения». Зачем Евклид сформулировал задачу «делении в крайнем и среднем отношении»? Анализ «Начал» Евклида показывает, что Евклид использовал эту задачу для геометрического построения равнобедренного треугольника с углами 36°, 72°,72°, называемого «золотым» равнобедренным треугольником, правильного пятиугольника, называемого пентагоном, и, наконец, додекаэдра, который считался в античной науке главной геометрической фигурой, выражающей «Гармонию Мироздания». Такое большое внимание Евклида к «золотому сечению», пентагону и додекаэдру привело к выдвижению весьма распространенной гипотезы о том, что главной целью, которую преследовал Евклид при написании своих «Начал», было изложение геометрической теории «Платоновых Тел», на основе которых Платон построил свою Космологию. Это означает, что в «Началах» Евклида блестяще была воплощена Пифагорейская доктрина о числовой гармонии мироздания», а сами «Начала» Евклида и можно рассматривать как исторически первую «Математическую теорию Гармонии».

После Евклида «Математика Гармонии» активно развивалась в эпоху Возрождения (Леонардо да Винчи, Лука Пачоли, Иоганн Кеплер), в 19-м веке (Люка, Бине, Клейн, Цейзинг и др.). В 20-м веке «Математика Гармонии» продолжала развивалаться под названием «Теория чисел Фибоначчи». Инициаторами этих исследований стали российский математик Николай Воробьев и американский математик Вернер Хоггатт, создатель Фибоначчи-Ассоциации. В книгах автора и статьях, опубликованных в последней четверти 20-го столетия, также были развиты некоторые важные аспекты приложений чисел Фибоначчи и «золотого сечения» в компьютерной науке (с перечнем этих публикаций автора можно познакомиться в статье [4]). Однако название «Теория чисел Фибоначчи» не только не отражает, а даже как бы сужает значение этого научного направления. Главной целью этого направления является не только изучение свойств чисел Фибоначчи, которые, действительно, широко встречаются в структурах и явлениях Природы, но создание более общих математических моделей Природы, не обязательно выражающихся с помощью классических чисел Фибоначчи. Чтобы расширить задачи и роль этого направления в развитии современной науки, автор в своем докладе «The Golden Section and Modern Harmony Mathematics» [6], сделанном на 7-й Международной конференции «Числа Фибоначчи и их приложения» (Австрия, Грац, 1996), предложил назвать развиваемое научное направление «Математикой Гармонии». Такое название четко отражает основную задачу этой математической теории – создание математических моделей «гармонических» процессов и структур Природы. Таким образом, в 1996 г. автором было введено название «Математики Гармонии» для обозначения нового междисциплинарного направления современной науки.

После 1996 г. автор продолжал развивать и углублять эту идею [7-22]. Однако, создание «Математики Гармонии» является итогом коллективного творчества, поскольку работы выдающихся исследователей в области чисел Фибоначчи и золотого сечения Николая Воробьева, Gardner Martin, H. S. M. Coxeter, George Polya, Verner Hoggat, Alfred Renyi, Stephen Vaida, Эдуарда Сороко, Олега Боднара, Николая Васютинского, Виктора Коробко, Иосифа Шевелева, Сергея Петухова, Roger Herz-Fishler, Jay Kappraff, Midhat Gazale, Vera W. de Spinadel, R.A. Dunlap, Scott Olsen, Александра Татаренко и других оказали непосредственное влияние на исследования автора в области «Математики Гармонии». Об этом детально написано в статье [5].

Возникает вопрос: сделаны ли в рамках «Математики Гармонии» некоторые «стратегические открытия», которые могут фундаментально повлиять на развитие современной науки? Действительно ли в ней есть неожиданные, непредсказуемые результаты, что является необходимым условием результативности той или иной теории? Для ответа на это вопрос, достаточно остановиться на новой теории гиперболических функций, разработанной в рамках «Математики Гармонии» [10, 20, 21]. В работе [21] новый класс гиперболических функций задается с помощью следующих формул.

Гиперблический синус Фибоначчи порядка m

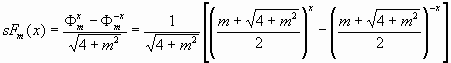(1)

Гиперболический косинус Фибоначчи порядка m

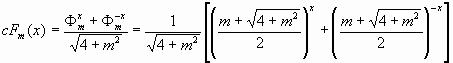(2)

Гиперболический синус Люка порядка m

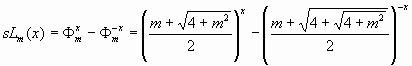(3)

Гиперболческий косинус Люка порядка m

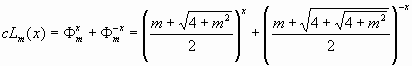(4)

В этих формулах x есть непрерывная переменная, а m – положительное действительное число, F _m - обобщенная золотая пропорция порядка m, которая выражается с помощью следующей формулы:

.

(5)

Заметим, что при m=1 формула (5) сводится к выражению для классической золотой пропорции

.

Заметим также, что если в формулах (1)-(4) непрерывную переменную x заменить дискретной перемннной k=0, ±1, ±2, ±3,..., то окажется, что формулы (1)-(4) превращаются в знаменитые «формулы Газале» [25], которые при различных m задают бесконечное число новых числовых последовательностей, в частности, числа Фибоначчи и Люка (m=1), числа Пелли и Пелли-Люка (m=2) и т.д.

Так как параметр m, входящий в формулы (1)-(4), является одним из действительных чисел, количество которых бесконечно, это означает, что число новых гиперболических функций типа (1)-(4) – бесконечно. Их столько же, сколько существует действительных чисел! Этот факт не может не вызывать удивления и даже восхищения формулами (1)-(4), которые содержат в себе столь богатую с математической точки зрения информацию.

Несколько слов о приоритете. Автор ни в коем случае не претендует на приоритет в открытии формулы (5). По мнению автора, к этой формуле независимо друг от друга пришли аргентинский математик Вера Шпинадель [24], египетский математик Мидхат Газале [25], американский математик Джей Капрафф [26] и российский исследователь Александр Татаренко [27]. Что касается формул (1)-(4), то они были выведены автором в статье [21] и являются своеобразным синтезом так называемых «формул Газале» [25] и симметричных гиперболических функций Фибоначчи и Люка, введенным Стаховым и Розиным в работе [10]. Эти факты являются еще одним подтверждением, что «Математика Гармонии» является бурно развивающимся интернациональным научным направлением, к развитию которого причастны ученые различных стран.

А теперь обратимся к гиперболической геометрии и теоретической физике, в частности, к таким «космологическим теориям», как «Геометрия Лобачевского» и «Геометрия Минковского» (гиперболическая интерпретация специальной теории относительности). Как известно, упомянутые «космологические теории» основываются на классических гиперболических функциях:

;

(6)

где е – основание натуральных логарифмов (одна из важнейших математических констант).

Легко показать, что для случая

= e

(7)

гиперболические функции Люка (3), (4) совпадают с классическими гиперболическими функциями (6) с точностью до постоянного коэффициента , а именно,

и .

(8)

Используя (7), после простых преобразований мы получим значение действительного числа m_e, для которого равенства (8) являются действительными:

.

(9)

Таким образом, классические гиперболичнеские функции, задаваемые (6), являются частным случаем более общего класса гиперболических функций, задаваемых формулами (1)-(4). А это означает, что если бы Лобачевский или Минковский знали бы о существовании формул (1)-(4), то геометрии Лобачевского и Минковского развивались бы совершенно по-другому. Но упущение Лобачевского и Минковского можно исправить, то есть можно разработать «золотые» геометрии Лобачевского и Минковского, основанные на новом классе гиперболических функций (1)-(4). И появление новых геометрий Лобачесвкого и Минковского не за горами. Это можно предсказать со стопроцентной уверенностью.

Это только один пример эффективного применения нового математического аппарата к гиперболической геометрии и теоретической физике. Эти примеры можно было бы продложить. Для этого достаточно прочитать работы автора [17, 18], посвященные разработке новой теории корректирующих кодов и нового вида криптографии, что имеет важное значение для современной информатики.

И эти примеры подтверждают, что разработка «Математика Гармонии» — это свершившийся факт современной науки. Интерес к «Математике Гармонии» в западной науке огромный. И это подтверждается большим интересом к статьям автора, проявленным в международном междисциплмнарном журнале «Chaos, Solitons and Fractals» (кстати, журнал был основан по инициативе выдающегося ученого славянского происхождения, Нобелевского Лауреата Ильи Пригожина). Все статьи автора, представленные в этот журнал, опубликованы в этом журнале с оценкой «excellent» [10-20]. Если не считать «пристального внимания» к работам автора со стороны «Комиссий по лженаукам» Российской академии наук и Академии наук Беларуси, то, если говорить серьезно, профессинальный интерес к работам автора проявлен и в российской науке. Об этом свидетельствует публикация большой (41 страница) заказной статьи автора «Золотое сечение, священная геометрия и математика гармонии», опубликованной в престижном физическом сборнике «Метафизика. Век XXI» [23].

«Математика Гармонии» является новым междисциплинарным направлением современной науки, которое может повлиять на различные области современной науки и стать источником следующих «золотых» проектов:

1. Теория вероятностей. Невозможно переоценить методологическое значение глубокой математической связи обобщенных p-чисел Фибоначчи с треугольником Паскаля и биномиальными коэффициентами. Ясно, что эта связь может стать началом переосмысливания многих разделов современной математики и теоретической физики, в которых комбинаторные отношения играют важную роль, в частности, теории вероятностей и статитических законов.

>2. Теория чисел. Новое «конструктивное» определение действительного числа, данное в [9], имеет «стратегическое» значение для развития теории чисел. Доказано, что существует бесконечное число «конструктивных» определений действительного числа, основанных на золотых p-пропорциях. Каждое из этих определений соответствует заданному целому числу p=0, 1, 2, 3,... и порождает некоторую оригинальную теорию действительных чисел.

3. Теория измерения. Как известно, теория измерения, основанная на аксиомах Евдокса-Архимеда и Кантора, является одной из фундаментальных теорий математики. С этой точки зрения «алгоритмическая теория измерения», разработанная автором, представляет фундаментальный интерес для развития математики.

4. Теория элементарных функций. Гиперболические функции Фибоначчи и Люка [10, 20, 21] являются новым классом «элементарных функций» и значительно расширяет теорию гиперболических функций. Тот факт, что число гиперболичиских функций, задаваемых (1)-(4), теоретически бесконечно и что каждая из новых гиперболических функций порождает рекуррентную последовательнось, подобную числам Фибоначчи, Люка или Пелли, представляет «стратегический» интерес для математики и теоретической физики.

5. Теория чисел Фибоначчи. «Математика Гармонии» создает новые стимулы для развития «теории чисел Фибоначчи». Прежде всего рекуррентные формулы для обобщенных р-чисел Фибоначчи и Люка расширяют область «фибоначчиевых» исследований. С другой стороны, гиперболические функции Фибоначчи и Люка [10, 20, 21] превращают «теорию чисел Фибоначчи» в «непрерывную» теорию, что позволяет применить к «теории чисел Фибоначчи» математический аппарат «непрерывной» математики, в частности, дифференцирование и и нтегрирование.

6. Теория матриц. Матрицы Фибоначчи [7, 17] и «золотые» матрицы [18] обладают уникальными математическими свойствами и могут быть выделены в особый класс матриц с детерминантом, равным +1 или -1. Изучение таких матриц представляет интерес для теории матриц. Поиск приложений этих матриц в теоретической физике является одним из важных направлений физических исследований.

7. Теоретическая физика. Мы можем указать на ряд важных приложений «Математики Гармонии» в современной теоретической и экспериментальной физике. Прежде всего, это «квазикристаллы Шехтмана», основанные на «Платоновом икосаэдре», и «фуллерены» (Нобелевская премия 1996 г.), основанные на «Архимедовом усеченном икосаэдре». Разработанная египетским ученым Ель Нашие теория «E-infinity», основанная на «золотом сечении», является плодотворным источником важных идей и приложений в квантовой физике. Общая теория гиперболических функций [21] может привести к пересмысливанию таких важных «космологических теорий» как «геометрия Лобачевского» и «геометрия Минковского» (гиперболическая интерпретация специальной теории относительности Эйнштейна). Исследования Николая Косинова [28-31] могут привести к открытию связей фундаментальных физических констант с «золотым сечением» и его обобщениями.

8. Философия. «Закон структурной гармонии систем», предложенный белорусским философом Эдуардом Сороко, возможно, является одним из наиболее выдающихся достижений сосременной философии. Этот закон является блестящим подтверждением эффективности применения «Обобщенного Принципа Золотого Сечения» [11] к самоорганизующимся системам.

9. Ботаника. Новая геометрическая теория ботанического явления филллотаксиса, развитая украинским архитектором Олегом Боднаром, является блестящим подтверждением того факта, что геометрия филлотаксисных объектов основана на гиперболических функциях Фибоначчи и Люка.

10. Биология. Рост биологических клеток является одной из фундаментальных проблем биологии. В статье [32] доказано, что деление биологических клеток является асимметричным и основано на обобщенных p-числах Фибоначчи.

11. Медицина. Российский биолог Виктор Цветков доказал в своей книге «Сердце, Золотое Сечение и Симметия» (1997), что сердечная деятельность млекопитающих основана на «принципе золотого сечения». По мнению Цветкова организация «золотого» кардиологического цикла является результатом длительной эволюции млекопитающих в направлении оптимизации их структуры и функций.

12. Генетика. Открытие «золотых» геноматриц, сделанное российским ученым Сергеем Петуховым, имеет оргромное значение для современной генетики. Это открытие показывает глубокую связь генетического кода с «золотым сечением», которое может рассматриваться как некоторый «универсальный код Природы» и основа живых организмов.

13. Компьютеры. «Фибоначчиевые» и «золотые» компьютерные арифметики, которые были разработаны автором, могут стать источником новых компьютерных проектов («помехоустойчивый процессор Фибоначчи», «золотой» отказоусточивый зеркально-симметричный процессор и т.д.).

14. Измерительные системы. «Золотые» резистивные делители являются электрической основой «золотых» самокорректирующихся аналого-цифровых и цифро-аналоговых преобразователей и могут привести к новым проектам в области измерительных систем.

15. Телекоммуникационные системы. Матрицы Фибоначчи являются математической основой новой теории кодирования [17], которая может эффективно использована для обнаружения и исправления ошибок в телекоммуникационных системах. «Золотые» матрицы привели к созданию «золотой» криптографии [18, 21], которая может быть использована для криптографической защиты информационных систем, работающих в реальном масштабе времени.

16. Музей Гармонии и Золотого Сечения ( http://www.goldenmuseum.com/) является уникальным историческим, естественно-научным и художественным музеем, которому нет аналогов в мировой культуре. Музей является коллекцией всех произведений Природы, Науки и Искусства, основанных на «золотом сечении», числах Фибоначчи и Платоновых телах.

17. Реформа математического образования. Основу программы «математического образования», используемой в средней школе, составляет «Элементарная математика», созданная в античной науке. Каждый студент хорошо знает «Теорему Пифагора», которая по выражению Кепплера является одним из «сокровищ» геометрии и выступает в роли некоторого символа «Элементарной математики». Но иногда многие так называемые «образованные люди» имеют весьма смутное представление о «золотом сечении», втором «сокровище» геометрии (Кеплер). «Математика Гармонии» является развитием и дополнением «Элементарной математики» и может стать основой для реформы математического образования, основанной на «золотом сечении». «Математика Гармонии» может превратить процесс изучения математики в захватывающий процесс поиска гармонических процессов в Природе, которая нас окружает.

18. Наука о Гармонии Систем. «Математика Гармонии» может стать основой «Науки о Гармонии Систем», важного междисциплинарного направления современной науки.

Таким образом, мы имеем полное право заявить, что «Математика Гармонии» вполне подпадает под общее определение математики, данное Колмогоровым, как «науки о количественных отношениях и пространственных формах действительного мира». В отличие от «чистой» математики «Математика Гармония» имеет тесные связи с современным естествознанием, в частности, с теоретичнеской физикой, ботаникой, генетикой, биологией, а также информатикой, и может стать источником плодотворных идей и концепций в развитии современной науки.

Литература

1. Стахов А.П. Сакральная геометрия и математика гармонии // «Академия Тринитаризма», М., Эл № 77-6567, публ.11176, 26.04.2004 http://www.trinitas.ru/rus/doc/0232/004a/02320028.htm
   
2. Стахов А.П. Математика Гармонии как новое междисциплинарное направление современной науки // «Академия Тринитаризма», М., Эл № 77-6567, публ.12371, 19.08.2005 http://www.trinitas.ru/rus/doc/0232/004a/02320001.htm
   
3. Стахов А.П. Гармония Мироздания и Золотое Сечение: древнейшая научная парадигма и ее роль в современной науке, математике и образовании. Часть 1 // «Академия Тринитаризма», М., Эл № 77-6567, публ.12840, 19.01.2006 http://www.trinitas.ru/rus/doc/0232/004a/02320036.htm
   
4. Стахов А.П. Гармония Мироздания и Золотое Сечение: древнейшая научная парадигма и ее роль в современной науке, математике и образовании. Часть 2 // «Академия Тринитаризма», М., Эл № 77-6567, публ.12855, 23.01.2006
   http://www.trinitas.ru/rus/doc/0232/004a/02320037.htm
   
5. А.П. Стахов, Три «ключевые» проблемы математики на этапе ее зарождения и новые направления в развитии математики, теоретической физики и информатики // «Академия Тринитаризма», М., Эл № 77-6567, публ.14135, 12.01.2007
   http://www.trinitas.ru/rus/doc/0232/004a/02321064.htm
   
6. Stakhov A.P. The Golden Section and Modern Harmony Mathematics. Applications of Fibonacci Numbers, Volume 7, 1998, 393-399.
   
7. Stakhov AP. A generalization of the Fibonacci Q-matrix. The journal «Reports of the National Academy of Sciences of Ukraine», 1999, No 9, 46-49.
   
8. Stakhov AP. Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic. The Computer Journal, 2002, Vol. 45, No. 2, 221-236.
   
9. Стахов А.П. Обощенные золотые сечения и новый подход к геометрическому определению числа. Украинский математический журнал, 2004, Том 56, №. 8, с. 1143-1150.
   
10. Stakhov A., Rozin B. On a new class of hyperbolic function. Chaos, Solitons & Fractals, 2005, Volume 23, Issue 2, 379-389.
    
11. Stakhov A.P. The Generalized Principle of the Golden Section and its applications in mathematics, science, and engineering. Chaos, Solitons & Fractals, 2005, Volume 26, Issue 2, 263-289.
    
12. Stakhov A., Rozin B. The Golden Shofar. Chaos, Solitons & Fractals, 2005, Volume 26, Issue 3, 677-684.
    
13. Stakhov A.P. Fundamentals of a new kind of Mathematics based on the Golden Section. Chaos, Solitons & Fractals 2006, Volume 27, Issue 5, 1124-1146.
    
14. Stakhov A., Rozin B. The «golden» algebraic equations. Chaos, Solitons & Fractals 2006, Volume 27, Issue 5, 1415-1421.
    
15. Stakhov A., Rozin B. Theory of Binet formulas for Fibonacci and Lucas p-numbers. Chaos, Solitons & Fractals, 2006, Volume 27, Issue 5, 1162-1177.
    
16. Stakhov A., Rozin B. The continuous functions for the Fibonacci and Lucas p-numbers. Chaos, Solitons & Fractals, 2006, Volume 28, Issue 4, 1014-1025.
    
17. Stakhov A. Fibonacci matrices, a generalization of the «Cassini formula», and a new coding theory. Chaos, Solitons & Fractals, 2006, Volume 30, Issue 1, 56-66.
    
18. Stakhov A. The «golden» matrices and a new kind of cryptography. Chaos, Solitons & Fractals 2007, Volume 32, Issue 3, 1138-1146.
    
19. Stakhov AP. The generalized golden proportions, a new theory of real numbers, and ternary mirror-symmetrical arithmetic. Chaos, Solitons & Fractals (in Press).
    
20. Stakhov AP, Rozin BN. The «golden» hyperbolic models of Universe. Chaos, Solitons & Fractals, (In Press).
    
21. А.П. Стахов, Формулы Газале, новый класс гиперболических функций Фибоначчи и Люка и усовершенствованный метод «золотой» криптографии // «Академия Тринитаризма», М., Эл № 77-6567, публ.14098, 21.12.2006. http://www.trinitas.ru/rus/doc/0232/004a/02321063.htm
    
22. Stakhov A.P., Rozin B.N. The Golden Section, Fibonacci series and new hyperbolic models of nature. Visual Mathematics, Volume 8, No 3, 2006 http://www.mi.sanu.ac.yu/vismath/stakhov/index.html
    
23. Стахов А.П. Золотое сечение, священная геометрия и математика гармонии. Сборник «Метафизика. Век XXI». Москва: Бином, 2006. – с. 174-215
    
24. Vera W. de Spinadel, From the Golden Mean to Chaos, Nueva Libreria (1998), second edition Nobuko (2004).
    
25. Gazale Midhat J. Gnomon. From Pharaohs to Fractals. Princeton, New Jersey: Princeton University Press, 1999 (русский перевод, 2002).
    
26. Kappraff Jay. Connections. The geometric bridge between Art and Science. Second Edition. Singapore, New Jersey, London, Hong Kong. World Scientific, 2001.
    
27. Татаренко А.А. «Т_m — принцип» — всемирный закон гармонии // «Академия Тринитаризма», М., Эл № 77-6567, публ.12575, 10.11.2005 http://www.trinitas.ru/rus/doc/0232/009a/02320002.htm
    
28. Косинов Н.В. Связь трех наиболее важнейших констант: постоянной тонкой структуры (α), числа (π) и золотого сечения (Φ) http://piramyd.express.ru/disput/kosinov/const3/text.htm
    
29. Косинов Н.В. Константы гармонических последовательностей http://filosof.net/disput/kosinov/kgp.htm
    
30. Косинов Н.В. Золотые инварианты гармонических последовательностей http://filosof.net/disput/kosinov/garm/text.htm
    
31. Косинов Н.В. Золотая проопрция, золотые константы и золотые теоремы http://filosof.net/disput/kosinov/gold/text.htm
    
32. Spears Colin Paul, Bicknell-Jonson Marjorie. Asymmetric cell division: binomial identities for age analysis of mortal vs. immortal trees. Applications of Fibonacci Numbers, Volume 7, 1998, 377-391.