В статье приводится обзор новых результатов в области «Математики Золотого Сечения», восходящей к «Началам» Евклида (Теорема 2.11). К числу этих результатов относятся: обобщение Теоремы Евклида о «делении в крайнем и среднем отношении», новый класс гиперболических функций — гиперболические функции Фибоначчи и Люка, обобщенные числа Фибоначчи, обобщенные золотые пропорции, обобщенный принцип золотого сечения, «золотые» алгебраические уравнения, обобщенные формулы Бине, обобщенные числа Люка, матрицы Фибоначчи, «золотые» матрицы. Рассматриваются приложения этих математических результатов в теории чисел, теории измерения, компьютерной арифметике, теории кодирования и криптографии.

We give in the article a survey of the new results in the «Mathematics of the Golden Section», going back in its origin to Euclid’s Elements, namely, a new class of hyperbolic functions, a generalization of Euclid’s Theorem II,11, a new class of hyperbolic functions — hyperbolic Fibonacci and Lucas functions, the generalized Fibonacci numbers, the generalized golden proportions, the generalized principle of the golden section, the golden algebraic equations, the generalized Binet formulas, the generalized Lucas numbers, Fibonacci matrices, the «golden» matrices. We consider applications of these mathematical results in number theory, measurement theory, computer arithmetic, coding theory and cryptography.

Key words. The golden section, Fibonacci and Lucas numbers, Binet formulas, measurement theory, number systems, hyperbolic functions, coding theory and cryptography

1. Introduction

A division in extreme and mean ratio (DEMR) in Euclid’s Elements

«The Elements» of Euclid is one of the most known mathematical work of ancient science. This scientific work was written by Euclid in the 3-d century B.C. It contains the main theories of the antique mathematics: elementary geometry, number theory, algebra, theory of proportions and ratios, methods of calculations of areas and volumes, etc. Euclid summed in this work the 300-year period of the development of the Greek mathematics and created a strong base to the further development of mathematics. During more than two millenia «The Elements» remained a basic work on the «Elementary Mathematics», which gave the origin of many fundamental theories of mathematics, in particular, geometry, number theory, measurement theory.

From «The Elements» of Euclid the following geometrical problem, which was named the problem of «Division in Extreme and Mean Ratio» (DEMR), came to us [1]. This problem was formulated in Book II of «The Elements» as follows.

Theorem II,11 (the area formulation of DEMR). To divide a line AB into two segments, a larger one CB and a smaller one AC so that

S(CB) = R(AB,AC).

(1)

Remind that S(CB) means the area of a square with a side CB and R(AB,AC) means the area of a rectangle with sides AB and AC.

We can rewrite expression (1) in the following form:

(CB)2 = ABґ AC

(2)

Divide now both parts of the expression (2) by CB and then by AC. Then the expression (2) takes a form of the following proportion:

, (3)

(3)

well-known for us as the «golden section».

We can interpret a proportion (3) geometrically: divide a line AB with a point C into two segments, a larger one CB and a smaller one AC so that a ratio of a larger segment CB to a smaller one AC is equal to a ratio of a line AB to a larger segment CB.

Designate a proportion (3) by x. Then, taking into consideration that АВ = АС + СВ, the proportion (3) can be written in the following form:

,

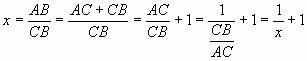from where the following algebraic equation follows:

x2 = x + 1

(4)

It follows from a «geometrical meaning» of the ratio (3), that the required solution of Eq. (4) has be a positive number; it follows from where that a positive root of Eq. (4) is a solution of the problem. If we designate this root by t, then we will get:

t = .

(5)

This number is called the golden proportion, golden mean, golden number or golden ratio.

Notice that there is the following identity, which connects powers of the golden ratio:

t n = t n-1 + t n-2 = t ґ t n-1

(6)

In Section 1 of Chapter 1 of the book [1] Roger Herz-Fishler analysis 84 Euclidean theorems, which, in his opinion, has relation to the DEMR, starting from Book I and ending by Book XIII. The most important of them are Theorem IV, 10 (an isosceles triangle with the angles 72° — 72° — 36°), Theorem IV, 11 (to inscribe a regular pentagon in a given circle), Theorem IV, 12 (to circumscribe a regular pentagon about a circle), Theorem IV, 13 (to inscribe a circle in a given regular pentagon), Theorem IV, 14 (to circumscribe a circle about a given regular pentagon), Theorem VI, def.3 (DEMR), Theorem VI, 30 (DEMR), Theorem XIII, 1, Theorem XIII, 4, Theorem XIII, 5, Theorem XIII, 6, Theorem XIII, 8, Theorem XIII, 9 (all about DEMR), Theorem XIII, 17 (to inscribe a dodecahedron in a sphere), Theorem XIII,18, Theorem XIII, 18 and so on. This means that DEMR goes by the «red thread» through Euclid’s Elements and is one of the most important geometrical ideas of Euclid’s Elements.

Why Euclid formulated Theorem II, 11? As is shown in [1] using this theorem he gave then a geometric construction of the «golden» isosceles triangle (Book IV), pentagon (Book IV), and dodecahedron (Book XIII). As is well known, the representation of the ancient Greeks about the Universe Harmony was connected with its embodiment in the Platonic Solids. Of course, that Plato’s ideas about the role of the regular polyhedra in the Universe structure influenced on Euclid’s Elements. In this famous book, which during centuries was the unique textbook on geometry, the description of the «ideal» lines and the «ideal» figures was given. A straight line is the most «ideal» line, and the regular polygons and polyhedrons are the most «ideal» geometric figures. It is interesting, that The Elements of Euclid begins from the description of equilateral triangle, which is the simplest regular polygon, and ends with studying of the five Platonic Solids. Notice, that a theory of the Platonic Solids are stated in the XIII, that is, final book of Euclid’s Elements. By the way, that fact, that the theory of the Platonic Solids was placed by Euclid in the final (that is, as though the most important) book of The Elements, became a reason, why the ancient Greek mathematician Proclus, who was Euclid’s commentator, put forward the interesting hypothesis about the true purposes of Euclid to write The Elements. In Proclus’ opinion, Euclid wrote The Elements with the purpose to give a full and systematized theory of geometric construction of the «ideal» geometric figures, in particular, the five Platonic Solids, in passing he gave in The Elements some advanced achievements of the Greek mathematics necessary to state theory of the «ideal» geometric figures! Thus, from such unexpected point of view we can consider The Elements of Euclid as the first historically geometric theory of the Universe Harmony, based on the Platonic Solids and DEMR (the golden section)!


See full text of this article at PDF format (509 Kb).