|
|
|
А.П. Стахов
и «золотые» геноматрицы Сергея Петухова
1.Введение
Из последних публикаций, касающихся приложений Золотого Сечения, наибольшее впечатление на меня произвела статья «Метафизические аспекты матричного анализа генетического кодирования и золотое сечение» [1], написанная доктором физико-математических наук, профессором Сергеем Валентиновичем Петуховым и опубликованная в научном сборнике «Метафизика. Век XXI» (Москва, БИНОМ, 2006), подготовленном кафедрой теоретической физики Московского университета. Кстати, в этом же сборнике опубликована и моя статья «Золотое сечение, священная геометрия и математика гармонии» [2].
Интересно, что наши научные пути с С.В. Петуховым очень тесно переплетаются. Наше заочное знакомство с Сергеем Валентиновичем началось из Международного сборника научных статей «Computers & Mathematics with Applications» (Volume 17, No 4-6, 1989). В этом сборнике была опубликована моя первая англоязычная статья [3]. Но в этом же сборнике была опубликована и большая статья С.В. Петухова – и, если мне не изменяет память, мы были едва ли не единственными советскими учеными, статьи которых были приняты для публикации в этом весьма престижном журнале (поговаривали даже, что рецензентами статей в этом сборнике были Лауреаты Нобелевской Премии). В период моей работы в Университете Эдуардо Мондлане (Мапуту, Мозамбик, 1998-2000) мне удалось установить электронную связь с проф. Петуховым и с тех пор она не прерывалась. В 2001 г. Сергей Валентинович прислал мне свою книгу «Бипериодическая таблица генетического кода и число протонов» [4], которую я прочитал с огромным интересом.
Но первая наша встреча состоялась 29-го мая 2003 г. в Москве, куда я приехал по приглашению проф. Владимирова (Московский университет) и проф. Петухова, чтобы сделать доклад «Новый тип элементарной математики и компьютерной науки, основанных на Золотом Сечении» на совместном научном семинаре «Геометрия и Физика» кафедры теоретической физики Московского университета (руководитель проф. Владимиров Ю.С) и Междисциплинарного семинара «Симметрия в науке и искусстве» при Институте машиноведения РАН (соруководитель проф. Петухов С.В.).
Доклад, как мне кажется, получился. Отчет об этом докладе выставлен на Интернете http://www.goldenmuseum.com/20ReportPres_rus.html. Было достаточно бурное обсуждение, в котором приняли известные московские ученые проф. Г.И. Шипов, проф. А.А. Зенкин, Николай Петрович Брусенцов (патриарх советской компьютерной науки), а также руководители семинаров профессора Ю.С. Владимиров и С.В. Петухов. Как мне показалось, наибольший интерес у Петухова вызвала та часть моего доклада, где я рассказывал о матрицах Фибоначчи. И действительно, буквально через неделю после моего выступления я получил в Виннице электронное письмо от С.В. Петухова, в котором он описывал какие-то странные матрицы, элементами которых были степени «Золотой Пропорции». Я ничего тогда не понял из его письма и ответил ему, что с подобными матрицами я не встречался. И только после ознакомления со статьей Петухова [1] я понял, что Сергей Валентинович «проверял» на мне новизну «золотых» геноматриц, к которым он пришел и о которых я расскажу ниже.
Но я хотел бы начать свой рассказ о «золотых» геноматрицах Петухова в контексте так называемого «матричного подхода» в «теории Золотого Сечения», развитие которого началось с работ известного американского математика Вернера Хоггатта, создателя Фибоначчи-Ассоциации.
2. Матричный подход в теории чисел Фибоначчи
2.1. Q-матрица (Verner Hoggatt)
С теорией Q-матрицы, развитой американским математиком Вернером Хоггаттом, создателем Фибоначчи-Ассоциации, я впервые познакомился, прочитав его книгу [5]. Под Q-матрицей понимается квадратная матрица размером 2ґ2 следующего вида:
|
|
(1) |
Заметим, что детерминант Q-матрицы равен -1, так как
Det Q = 1ґ 0 — 1ґ 1 = — 1.
Наиболее интригующее свойство Q-матрицы состоит в том, что она имеет непосредственное отношение к числам Фибоначчи. Действительно, если возвести Q-матрицу в в n-ю степень, где n=0, ± 1, ± 2, ± 3,..., то мы получим следующую матрицу:
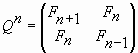 , , |
(2) |
элементами которой являются числа Фибоначчи Fn-1, Fn, Fn+1!
Естественно, что это факт не мог не вызвать прилив огромного энтузиазма у американских математиков- фибоначчистов, прежде всего у создателя Фибоначчи-Ассоциации Вернера Хоггатта, и они достаточно быстро разработали теорию Q-матрицы. Оказалось, что Q-матрица является в некотором смысле уникальной матрицей и играет среди квадратных матриц такую же роль, как число «золотая пропорция» среди действительных чисел.
Рассмотрим некоторые свойства Q-матрицы. Прежде всего, определим детерминант матрицы (2). Из теории матриц известно следующее соотношение для детерминанта квадратной матрицы, возведенной в степень n:
| Det (Qn) = (Det Q)n. | (3) |
Но ранее мы установили, что Det Q = -1; подставляя это значение в формулу (3), мы получим следующий результат:
| Det Qn = (-1)n, | (4) |
где n — целое число, принимающее значение из множества {0, ± 1, ± 2, ± 3,...}.
Но если мы теперь вычислить детерминант матрицы (2) по традиционным правилам вычисления детерминанта, а затем использовать тождество (4), тогда мы получим хорошо нам известное тождество, связывающее три соседних числа Фибоначчи и известное в теории чисел Фибоначчи под названием «формулы Кассини» [6]:
| Det Qn = Fn-1 Fn+1 — |
(5) |
Таким образом, это означает, что Q-матрица выражает одно из наиболее важных свойств чисел Фибоначчи, задаваемое (5)!
2.2. Qp-матрицы (А.П. Стахов)
Из книги [5] основателя Фибоначчи-ассоциации Вернера Хогатта я был знаком с теорией «фибоначчиевой» Q-матрицы. Однако после Фибоначчи-конференции (Австрия, Грац, 1996 г.) мой интерес к этому направлению значительно возрос. На Фибоначчи-конференции я познакомился с известным математиком-фибоначчистом Marjorie Bicknell-Johnson, ученицей и сподвижницей Вернера Хоггатта. Она прислала мне несколько наиболее значительных статей и всю библиографию по Q-матрицам, и я увлекся этой проблемой.
Моя идея состояла в следующем. Еще в 1966 г. мы с Игорем Витенько пришли к новым числовым последовательностям, названным обобщенными числами Фибоначчи или р-числами Фибоначчи. При заданном целом р=0, 1, 2, 3,... эти числовые последовательности задавались следующей рекуррентной формулой:
| Fp(n+1) = Fp(n)+Fp(n-p) | (6) |
при следующих начальных условиях:
| Fp(1) = Fp(2) =... = Fp(p+1) = 1 | (7) |
Оказывается, что при различных значениях р рекуррентная формула (6) при начальных условиях (7) «генерирует» бесконечное количество числовых последовательностей. При р=0 это будет широко известный нам «двоичный» ряд чисел: 1, 2, 4, 8, 16,.... А вот при р=1 рекуррентная формула (6) при начальных условиях (7) «генерирует» знаменитый «ряд Фибоначчи»: 1, 1, 2, 3, 5, 8, 13, 21,..., открытый еще в 13-м веке известным итальянским математиком Леонардо из Пизы (по прозвищу Фибоначчи).
Ясно, что р-чисела Фибоначчи представляют собой более общий класс числовых последовательностей, чем классические числа Фибоначчи. Но если Q-матрица (1) соответствует классическим числам Фибоначчи, то возникает вопрос: нельзя ли придумать матрицы подобного типа, соответствующие р-числам Фибоначчи. После Фибоначчи-конференции (1996 г.) я начал размышлять над этим вопросом. В одну из душных ночей жаркой ливийской осени 1996 г. (я в то время работал профессором кафедры компьютерной техники Университета Аль Фатех, Триполи, Ливия) я проснулся с готовым решением. Перед моими глазами возникла матрица следующего вида:
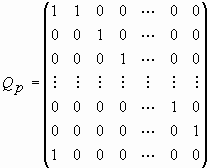 |
(8) |
Такую матрицу я назвал Qp-матрицей, где р=0, 1, 2, 3, …. А теперь я призываю читателя вместе со мной насладиться удивительными свойствами Qp-матрицы. Прежде всего, исследуем структуру Qp-матрицы. Легко увидеть, что в общем виде Qp-матрица представляет собой квадратную матрицу размером (p+1)ґ (p+1), где р – заданное целое число, принимающее значение из множества {0, 1, 2, 3, …}. А теперь внимательно посмотрим на Qp-матрицу (8). Все элементы Qp-матрицы равны 0 или 1. Мы видим, что она состоит из единичной матрицы размером рґ р, окруженной первым столбцом, начинающимся и заканчивающимся 1, и последней строки, начинающейся с 1.
Рассмотрим теперь частные случаи Qp-матрицы, соответствующие значениям p = 0, 1, 2, 3, 4:
Q0 = (1); ![]() ;
; 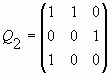 ;
;
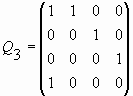 ;
; 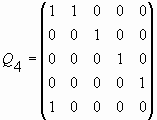 .
.
А теперь сравним между собой две соседние Qp-матрицы, например, матрицы Q4 и Q3. Существует ли между ними какая-то регулярная связь? Очень просто увидеть, что, если в матрице Q4 вычеркнуть последний, то есть 5-й столбец и предпоследнюю, т.е. 4-ю, строку, то мы получим матрицу Q3. Оказывается, что это – общий принцип, связывающий любые две соседние Qp-матрицы! Действительно, если в матрице Q3 вычеркнуть последний столбец и предпоследнюю строку, то мы придем к матрице Q2. Проделав то же самое с матрицей Q2, то есть, вычеркнув из нее последний столбец и предпоследнюю строку, мы придем к матрице Q1, которая представляет собой ни что иное, как классическую Q–матрицу, предмет восторга математиков-фибоначчистов. Таким образом, каждая Qp-матрица содержит в себе все предыдущие матрицы и, с другой стороны, входит в качестве составной части во все всех последующие матрицы. Конечно, когда я это обнаружил, душа моя наполнилась гордостью от того, что мне удалось придумать такую квадратную матрицу; и я понял, что в моих руках интересное математическое открытие! И я начал интенсивно исследовать математические свойства матрицы (8), для чего пришлось углубиться в теорию матриц.
Одной из важнейших интегральных характеристик квадратной матрицы, связывающей все ее элементы, является ее детерминант. Изучая свойства детерминантов матриц, в одной из книг по теории матриц я нашел ключевой принцип, который позволил мне определить детерминант любой Qp-матрицы (8). Выше я установил общий принцип, связывающий две соседние матрицы типа (8), например, матрицу Qp и матрицу Qp-1. Для этого в матрице Qp надо вычеркнуть последний, то есть, (р+1)-й столбец и предпоследнюю, то есть, р-ю строку. Заметим, что сумма р+1+р = 2р+1 всегда является нечетным числом независимо от четности числа р. И вот неожиданно я «наткнулся» на одну из общих теорем, задающих удивительно простую связь между детерминантами двух матриц, одна из которых (В) получается из предыдущей (А) путем вычеркивания в матрице А столбца и строки, на пересечении которых стоит «единичный» элемент 1, а остальные элементы вычеркиваемых «кортежей» равны нулю. Оказывается, что при таком вычеркивании детерминант новой матрицы В отличается от детерминанта исходной матрицы А только знаком, то есть между детерминантами матриц сохраняется следующее соотношение:
| Det B = — Det A. | (9) |
Это и есть тот «ключевой принцип», позволивший мне сразу же определить значение детерминанта для любой матрицы Qp. Действительно, рассмотрим две соседние матрицы Q1 и Q2. Детерминант матрицы Q1 нам известен: он равен -1. С другой стороны, матрица Q1 получается из матрицы Q2 путем вычеркивания 3-го столбца и 2-й строки, причем на их пересечении стоит 1. Но тогда согласно (9) мы легко находим значение детерминанта матрицы Q2 — он равен (+1). Но тогда, продолжая те же рассуждения для матриц Q2 и Q3, мы находим, что детерминант матрицы Q3 будет равен (-1), а матрицы Q4 равен (+1) и т.д. Другими словами, для всех матриц Qp, соответствующих нечетным значениям р (р=1, 3, 5, …) детерминант матрицы Qp равен (-1), а для матриц Qp с четными значениями р (р=0, 2, 4, …) детерминант равен (+1). Математически этот общий результат можно выразить так:
| Det Qp = (-1)р. | (10) |
Рассмотрим теперь матрицу ![]() , являющуюся n-й степенью Qp-матрицы (8). Я не хотел бы утомлять читателей математическими рассуждениями, которые привели меня к следующему результату:
, являющуюся n-й степенью Qp-матрицы (8). Я не хотел бы утомлять читателей математическими рассуждениями, которые привели меня к следующему результату:
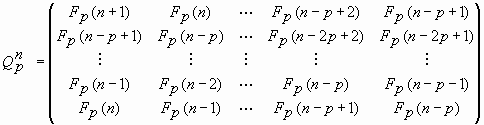 |
(11) |
где элементами матрицы ![]() выражаются через p-числа Фибоначчи, вытекающие из треугольника Паскаля. И этот результат является еще одним «секретом» треугольника Паскаля!
выражаются через p-числа Фибоначчи, вытекающие из треугольника Паскаля. И этот результат является еще одним «секретом» треугольника Паскаля!
А сейчас мы попытаемся вычислить детерминант матрицы (11). На первый взгляд, кажется, что эта проблема является чрезвычайно сложной. Но она кажется сложной только для тех, кто не знает теории матриц. Действительно, используя свойство (3), мы можем записать:
| Det |
(12) |
Подставляя выражение (10) в (12), мы можем переписать выражение (12) в виде:
| Det Qp = (-1)pn, | (13) |
где p = 0, 1, 2, 3, …; n = 0, ± 1, ± 2, ± 3, ….
И теперь мы можем выразить наше восхищение по поводу результата (13) и могущества математики! Действительно, невозможно вообразить, что p-числа Фибоначчи, вытекающие из «треугольника Паскаля», могут стать основой нового класса квадратных матриц, задаваемых выражениями (8) и (11). А результат (13) кажется нам абсолютно невероятным! Невозможно вообразить, чтобы для любого заданного р и n детерминант любой матрицы (11) (а число таких матриц бесконечно!) был всегда равен либо (+1), либо (-1), что следует из (13)! Возникает ощущение какой-то магии, какая заключена в матрицах (8) и (11).
Сразу после возвращения из Ливии я рассказал о своем новом результате в области теории матриц академику Митропольскому Ю.А. и он сразу же предложил мне опубликовать этот результат в «Докладах Академии наук Украины». Я подготовил статью «A generalization of the Fibonacci Q-matrix» и по рекомендации Юрия Алексеевича она была опубликована (на английском языке) в «Докладах Национальной академии наук Украины» (1999, №9) [7].
2.3. Новая теория кодирования
В настоящее время трудно предсказать значение теории ![]() -матриц, задаваемых (11), и их приложений в различных областях математики, физики и других наук. Однако ясно, что этот результат имеет фундаментальное значение для развития науки. С помощью этого результата мне удалось связать треугольник Паскаля с теорией матриц и открыть новый класс квадратных матриц, обладающих удивительным математическим свойством (13).
-матриц, задаваемых (11), и их приложений в различных областях математики, физики и других наук. Однако ясно, что этот результат имеет фундаментальное значение для развития науки. С помощью этого результата мне удалось связать треугольник Паскаля с теорией матриц и открыть новый класс квадратных матриц, обладающих удивительным математическим свойством (13).
Однако одно важное приложение мне удалось все же найти. В Мозамбике, где я работал профессором кафедры математики и информатики Университета Эдуардо Мондлане в период с 1998 по 2000, мне удалось разработать новую теорию кодированию, основанную на использовании Qp-матриц. Я не буду останавливаться более подробно на новой теории кодирования, отсылая читателей к работам [8, 9]. Отмечу только, что речь идет о принципиально новом («матричном») подходе к теории корректирующих кодов, когда объектами коррекции ошибок являются не биты и их комбинации (как это принято в классической теории кодирования), а числа, которые являются элементами матриц. При этом корректирующая способность новых кодов весьма значительна и превышает классические корректирующие коды в сотни и тысячи раз.
2.4. Гиперболические функции Фибоначчи и Люка
(А.П. Стахов, И.С. Ткаченко, Б.Н. Розин)
Перед тем, как приступить к рассказу о «золотых» матрицах, разработанных мною в Канаде, я хотел бы рассказать еще об одном математическом открытии, которое предшествовало «золотым» матрицам и к которому я имею непосредственное отношение. Речь идет о так называемых гиперболических функциях Фибоначчи и Люка, разработанных мною совместно с И.С. Ткаченко и Б.Н. Розиным [10-13].
В своих истоках эти функции восходят к знаменитым «формулам Бине», введенным в 19-м столетии французским математиком Бине (1786 — 1856)
Формулы Бине для чисел Фибоначчи Fn имеют следующий вид:
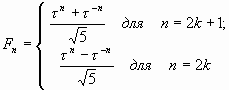 |
(14) |
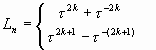 |
(15) |
где t = ![]() - «золотая пропорция».
- «золотая пропорция».
Анализ формул (14), (15) дает нам возможность ощутить истинное «эстетическое наслаждение» и еще раз убедиться в мощи человеческого разума. Действительно, ведь мы знаем, что числа Фибоначчи и Люка всегда являются целыми числами. С другой стороны, любая степень золотой пропорции является иррациональным числом. Отсюда вытекает, что любое число Фибоначчи или Люка с помощью формул (14), (15) может быть выражено через «золотую пропорцию». Например, трудно вообразить, что число Фибоначчи 5 может быть выражено в следующем виде:
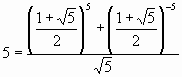
но это только частный случай формулы (14).
Анализ формул (14), (15) показывает, что по своей структуре они напоминают гиперболические функции. Эта аналогия между формулами Бине и гиперболическими функциями и стала отправной точкой для введения нового класса гиперболических функций, названных гиперболическими функциями Фибоначчи и Люка [10-13].
В качестве примера рассмотрим так называемые симметричные гиперболические функции Фибоначчи [13], которые нам понадобятся при выводе выражений для «золотых» матриц.
Симметричный гиперболический синус Фибоначчи
| (16) |
Симметричный гиперболический косинус Фибоначчи
| (17) |
Заметим, что числа Фибоначчи однозначно определяются через симметричные гиперболические синусы и косинусы Фибоначчи следующим образом:
| (18) |
То есть, согласно (18) числам Фибоначчи с четными номерами всегда соответствует симметричный фибоначчиевый синус sFs(x), а с нечетными номерами – симметричный фибоначчиевый косинус cFs(x). Таким образом, гиперболические функции Фибоначчи являются обобщением чисел Фибоначчи на непрерывную область.
Доказано, что каждому «фибоначчиевому» тождеству соответствует некоторое «непрерывное» тождество, выраженное в терминах гиперболических функций Фибоначчи, и наоборот. Например, знаменитая «формула Кассини» (5) в терминах симметричных гиперболических функций Фибоначчи представляется в виде двух «непрерывных» тождеств:
| [sFs(x)]2 — cFs(x+1) сFs(x-1) = -1 | (19) |
| [cFs(x)]2 — sFs(x+1) sFs(x-1) = 1, | (20) |
которые можно рассматривать как обобщение «формулы Кассини» (5) на непрерывную область.
В этой связи уместно вспомнить две известные формулы для тригонометрических и гиперболических функций:
sin2x + cos2x = 1 и ch2x – sh2x = 1,
которые играют в теории тригонометрических и гиперболических функций, по-видимому, ту же роль, что и формулы (19), (20) в теории гиперболических функций Фибоначчи.
2.5. «Золотые» матрицы (А.П. Стахов)
«Золотые» матрицы, к которым я пришел в 2004 г., являются своеобразным синтезом гиперболических функций Фибоначчи (16), (17) и Q-матрицы (2), теория которой разработана американским математиком Вернером Хоггатом [5]. Но если учесть, что в основе гиперболических функций Фибоначчи (16), (17) лежат формулы Бине (14), выведенные еще в 19-м веке, то можно сказать, что «золотые» матрицы являются итогом почти 200-летнего периода в развитии теории чисел Фибоначчи, начиная от французского математика 19-го века Бине и заканчивая 21-м веком.
Для вывода выражений для «золотых» матриц представим формулу (2), задающую n-ю степень Q-матрицы, в виде двух формул для четных (n=2k) и нечетных (n=2k+1) значений n:
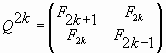 |
(21) |
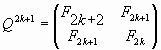 |
(22) |
Используя соотношение (18), мы можем выразить выражения (21), (22) в терминах симметричных гиперболических функций Фибоначчи:
| (23) |
| (24) |
где k – дискретная переменная, k=0, ± 1, ± 2, ± 3, ….
Если теперь заменить дискретную переменную k в матрицах (23), (24) непрерывной переменной x, тогда мы придем к двум необычным матрицам, которые являются функциями непрерывной переменной x:
| (25) |
| (26) |
При этом элементами матриц (25), (26) являются гиперболические функции Фибоначчи, задаваемые (16), (17).
Если теперь мы вычислим детерминанты «золотых» матриц (25), (26), то используя тождества (19), (20), мы придем к следующим необычным тождествам:
| Det Q2x = 1 | (27) |
| Det Q2x+1 = - 1 | (28) |
Это означает, что детерминанты «золотых» матриц (25), (26) не зависят от значения переменной x, то есть для любого значения x детерминант матрицы (25) тождественно равен (+1), а детерминант матрицы (26) тождественно равен (-1). Ясно, что результат (27), (28) производит некоторое «магическое» впечатление!
2.6. «Золотая» криптография
В 2004 г. мне удалось разработать оригинальный метод криптографической защиты дискретных сигналов, основанный на использовании «золотых» матриц. Статья на эту тему принята к публикации в журнале «Chaos, Solitons & Fractals» [14].
3. «Золотые» геноматрицы
(С.В. Петухов)
3.1. Генетическое кодирование
Открытие генетического кода, общего для всех живых организмов – от бактерии до человека – привело к развитию информационной точке зрения на живые организмы. Как подчеркивается в [1], «с этой точки зрения организмы представляют собой информационные сущности. Они существуют потому, что получают наследственную информацию от своих предков и живут для того, чтобы передать свой информационный генетический код потомкам. При таком подходе все остальные физические и химические механизмы, представленные в живых организмах, можно трактовать как вспомогательные, способствующие реализации этой основной – информационной – задачи».
Основы языка наследственной информации поразительно просты. Для записи генетической информации в рибонуклеиновых кислотах (РНК) любых организмов используется «алфавит», состоящий из четырех «букв» или азотистых оснований: аденин (А), цитозин (С), гуанин (G), урацил (U) (в ДНК вместо урацила используется родственный ему тимин (Т)).
Генетическая информация, передаваемая молекулами наследственности (ДНК и РНК), определяет первичное строение белков живого организма. Каждый кодируемый белок представляет собой цепи из 20 видов аминокислот. Триплетом называется блок из трех соседних азотистых оснований. Из четырехбуквенного алфавита можно составить всего 43=64 триплетов. Генетический код называется вырожденным, поскольку 64 триплета кодируют всего 20 аминокислот. Если произвольная белковая цепь содержит n аминокислот, то соответствующая ему последовательность триплетов в молекуле ДНК содержит 3n азотистых оснований или, другими словами, задается 3n-плетом. Белковые цепи обычно содержат сотни аминокислот и соответственно задаются весьма длинными полиплетами.
3.2. Матричное представление генетических полиплетов
Основная идея С.В. Петухова состоит в том, чтобы представлять генетические полиплеты в матричном виде. Простейшей является квадратная матрица второго порядка Р, которая используется для представления системы из четырех азотистых оснований («букв») генетического алфавита:
| (29) |
Далее С.В. Петухов предлагает рассматривать семейство всех одинаковых по длине генетических полиплетов в виде соответствующего семейства матриц Р(n), представляющих собой тензорные (кронекеровы) степени исходной матрицы (29). В качестве примеров ниже построены матрицы Р(2) и Р(3):
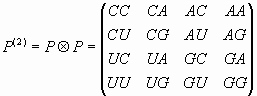
|
(30) |
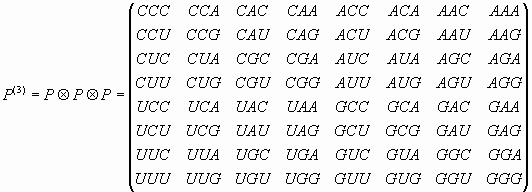 |
(31) |
Матрицы Р(n) названы геноматрицами. Данное семейство геноматриц Р(n) при достаточно большом n представляют всю систему генетических кодовых полиплетов, включая моноплеты генетического алфавита (29) и триплеты, кодирующие аминокислоты (31).
В каждом из четырех квадрантов геноматрицы Р(n) собраны все n-плеты, начинающиеся с одной буквы C, A, U, G. Если не обращать внимания на первую букву в n-плетах, то легко видеть, что квадрант матрицы Р(n) полностью воспроизводит матрицу Р(n-1) предыдущего поколения. С другой стороны, каждая матрица Р(n) образует квадрант матрицы Р(n+1) старшего поколения. Таким образом, геноматрица каждого нового поколения содержит в себе в скрытом виде информацию о всех предыдущих поколениях. Здесь уместно провести аналогию между геноматрицами Р(n) и Qp-матрицами (8), которые обладают подобным свойством, так как любая Qp-матрица (8) содержит в себе информацию о всех предыдущих матрицах Qp-1, Qp-2,..., Q1, Q0, но, с другой стороны, входит во все последующие матрицы Qp+1, Qp+2, Qp+3,....
3.3. Числовые геноматрицы
При замене в символьных матрицах каждого символа азотистых оснований на те или иные их количественные параметры получаются соответствующие числовые геноматрицы. Для образования таких количественных параметров С.В. Петухов предлагает воспользоваться числовыми значениями комплементарных водородных связей в азотистых основаниях генетического кода, «которые давно подозреваются на особую информационную значимость». Речь идет о двух и трех водородных связях, соединяющих комплементарные пары азотистых оснований в молекулах наследственности, причем для оснований C и G число таких водородных связей равно 3, а для A и U равно 2. Ключевая идея Петухова состоит в том, чтобы заменить каждый полиплет во всех матрицах Р(n) произведением чисел водородных связей его азотистых оснований. При этом, например, триплет CGA в октетной матрице (31) заменяется на произведение 3ґ 3ґ 2=18.
В результате такой замены символьные геноматрицы (29), (30), (31) превращаются соответственно в следующие числовые геноматрицы Рмульт:
| (32) |
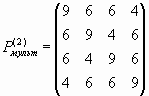 |
(33) |
 |
(34) |
Легко обнаружить ряд интересных свойств числовых геноматриц (32), (33), (34). Во-первых, все матрицы (32), (33), (34) являются симметричными относительно обеих диагоналей и поэтому названы бисимметричными [1]. Во-вторых, сумма чисел в каждой строке и каждом столбце матриц (32), (33) и (34) соответственно равны 5, 52=25 и 53 = 125, а общая сумма чисел в матрицах (32), (33), (34) соответственно равны 10, 102=100 и 103 = 1000. Доказано [1], что подобным свойством обладает любая числовая геноматрица матрица ![]() , поскольку каждая такая матрица является бисимметричной, при этом сумма чисел в каждой ее строке и каждом ее столбце равна 5n, а общая сумма чисел в матрице равна 10n. Уже эти удивительные свойства числовых геноматриц Петухова вызывают прямо-таки «магическое» впечатление. Но связь этих числовых геноматриц с «золотым сечением», обнаруженная Петуховым, производит совершенно невероятное впечатление!
, поскольку каждая такая матрица является бисимметричной, при этом сумма чисел в каждой ее строке и каждом ее столбце равна 5n, а общая сумма чисел в матрице равна 10n. Уже эти удивительные свойства числовых геноматриц Петухова вызывают прямо-таки «магическое» впечатление. Но связь этих числовых геноматриц с «золотым сечением», обнаруженная Петуховым, производит совершенно невероятное впечатление!
3.4. «Золотые» геноматрицы
Рассмотрим числовую геноматрицу (32), соответствующую простейшей символьной геноматрице (29).
А теперь рассмотрим квадратную матрицу Ф(1), элементами которой являются числа ![]() («золотая пропорция») и
(«золотая пропорция») и ![]() :
:
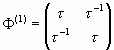 |
(35) |
Если теперь возвести матрицу (35) в квадрат, то в результате получается матрица следующего вида:
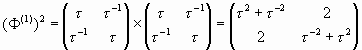 |
(36) |
А теперь вспомним формулу Бине для чисел Люка, задаваемую (15). Из этой формулы вытекает, что сумма t 2 + t -2 = L2 = 3. И тогда выражение (36) принимает следующий вид:
| (37) |
откуда вытекает, что числовой геноматрице (32) соответствует «золотая» геноматрица (35), которая после ее возведения в квадрат превращается в числовую геноматрицу (32)!
Но может быть, это случайное совпадение? Для ответа на этот вопрос рассмотрим числовую геноматрицу (33). Поставим ей в соответствие «золотую» геноматрицу, сформированную из соответствующей символьной геноматрицы (30) по следующему правилу.
Правило Петухова. Для получения «золотой» геноматрицы из соответствующей символьной матрицы необходимо каждый полиплет исходной символьной матрицы заменить произведением следующих числовых значений для его букв: C=G=t, A=U=t -1.
В результате применения «Правила Петухова» к символьной геноматрице (30) получаем следующую «золотую» геноматрицу:
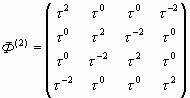 |
(38) |
А теперь возведем матрицу (38) в квадрат. В результате получим:
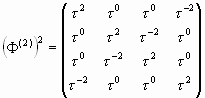 ґ ґ 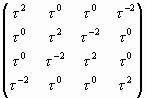 = == 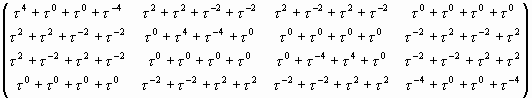 |
(39) |
Если теперь обратиться к формуле Бине (15) для чисел Люка, то можно записать следующие тождества:
| t 2 + t -2 = 3 и t 4 + t -4 = 7 | (40) |
С учетом тождеств (40) матрица (39) может быть представлена в следующем числовом виде:
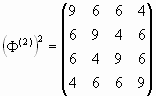 |
(41) |
Сравнивая (41) и (33), мы можем записать:
| (42) |
то есть числовой геноматрице (33) соответствует «золотая» геноматрица (38), которая после ее возведения в квадрат превращается в числовую геноматрицу (33)!
В качестве примера рассмотрим «золотую» геноматрицу ![]() , соответствующую символьной октетной геноматрице (31), которая задает триплеты, кодирующие аминокислоты:
, соответствующую символьной октетной геноматрице (31), которая задает триплеты, кодирующие аминокислоты:
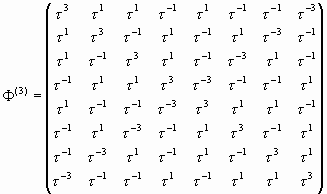 |
(43) |
Для этой матрицы также справедливо следующее соотношение:
| (44) |
Оказывается, что подобное соотношение справедливо для любой мультипликативной геноматрицы ![]() , то есть С. В. Петуховым доказано следующее утверждение, которые мы будем называть «Открытием Петухова».
, то есть С. В. Петуховым доказано следующее утверждение, которые мы будем называть «Открытием Петухова».
Открытие Петухова. Пусть А (аденин), С (цитозин), G (гуанин) и U (урацил) – азотистые основания («буквы») генетического алфавита, образующие исходную символьную матрицу ![]() . Тогда каждой символьной геноматрице типа
. Тогда каждой символьной геноматрице типа ![]() и членами которой являются полиплеты, составленные из «букв» генетического алфавита A, C, G и U, соответствует некоторая числовая геноматрица типа
и членами которой являются полиплеты, составленные из «букв» генетического алфавита A, C, G и U, соответствует некоторая числовая геноматрица типа ![]() , каждый член которой представляет собой произведение чисел водородных связей соответствующих азотистых оснований данного полиплнта, а каждой числовой геноматрице
, каждый член которой представляет собой произведение чисел водородных связей соответствующих азотистых оснований данного полиплнта, а каждой числовой геноматрице ![]() , в свою очередь, соответствует некоторая «золотая» геноматрица Ф(n), которая образуется из символьной геноматрицы Р(n) путем замены каждого полиплета произведением следующих числовых значений для его «букв»: C=G=t, A=U=t -1. При этом «золотая» геноматрица Ф(n) связана с числовой геноматрицей
, в свою очередь, соответствует некоторая «золотая» геноматрица Ф(n), которая образуется из символьной геноматрицы Р(n) путем замены каждого полиплета произведением следующих числовых значений для его «букв»: C=G=t, A=U=t -1. При этом «золотая» геноматрица Ф(n) связана с числовой геноматрицей ![]() следующим фундаментальным соотношением:
следующим фундаментальным соотношением:
(Ф(n))2 = ![]() .
.
Обнаружение связи «Золотого Сечения» с параметрами генетического кода позволило Петухову предложить новое – «матрично-генетическое» – определение золотого сечения.
Определение Петухова. Золотое сечение и его обратная величина (t и t-1) представляют собой единственные матричные элементы бисимметричной матрицы Ф, являющейся корнем квадратным из такой бисимметричной числовой матрицы Рмульт второго порядка, элементами которой являются генетические числа водородных связей (C=G=3, A=U=2) и которая имеет положительный детерминант.
4. Заключение
Итак, матричный подход в «теории Золотого Сечения» оказался весьма плодотворным и привел к следующим научным результатам:
- Первым результатом в этом направлении явилась разработка теории Q-матрицы (Verner Hoggatt), которая обнаруживает фундаментальную связь с числами Фибоначчи. Выражение для детерминанта n-й степени Q-матрицы в компактной форме задает «формулу Кассини», которая считается едва не главным математическим тождеством, связывающим соседние числа Фибоначчи.
- Дальнейшим развитием теории Q-матрицы является теория Qр-матриц (А.П. Стахов), которые связаны с р-числами Фибоначчи, открытыми во второй половине 20-го века при исследовании «диагональных сумм» треугольника Паскаля.
- Еще одним математическим достижением в этом направлении являются «золотые» матрицы (А.П. Стахов), которые основаны на Q-матрице и гиперболических функциях Фибоначчи.
- Теория Qр-матриц и «золотых» матриц привела к созданию новой теории кодирования и нового метода криптографии [8, 9, 14] (А.П. Стахов).
- Но главным научным открытием в этом направлении являются «золотые» геноматрицы, разработанные С.В. Петуховым. Открытие Петухова показывает фундаментальную роль, которую играет «Золотое Сечение» в генетическом кодировании. Открытие Петухова свидетельствует о том, что ЗОЛОТОЕ СЕЧЕНИЕ ЛЕЖИТ В ОСНОВЕ ЖИВОЙ ПРИИРОДЫ! Сейчас еще трудно оценить в полной мере революционный характер «открытия Петухова» для развития современной науки. Ясно одно, что для теории генетического кодирования – это результат такой же значимости, как и открытие самого генетического кода!
И мне хотелось бы закончить эту статью цитатой из статьи С.В. Петухова [1], которая подчеркивает важность матричного подхода в «теории Золотого Сечения»:
«Выдвинутое положение о матричном определении и матричной сущности золотого сечения дает эвристическую возможность рассмотреть весь этот материал на предмет его содержательной интерпретации с принципиально новой – матричной – точки зрения. Автор полагает, что многие реализации золотого сечения в живой и неживой природе связаны именно с матричной сущностью и матричным представлением золотого сечения. Математика золотых матриц – новая математическая веточка, изучающая, в частности, рекуррентные соотношения между рядами золотых матриц, а также моделирование с их помощью природных систем и процессов».
Литература
- Петухов С.В. Метафизические аспекты матричного анализа генетического кодирования и золотое сечение. Метафизика. Москва, Бином, 2006. — 216-250
- Стахов А.П. Золотое сечение, священная геометрия и математика гармонии. Метафизика. Москва, Бином, 2006. — 174-215.
- Stakhov A.P. The Golden Section in the measurement theory. An International Journal «Computers & Mathematics with Applications», Volume 17, No 4-6, 1989.
- Петухов С.В. Бипериодическая таблица генетического кода и число протонов. Москва, «Молодежный книжный центр», 2001.
- Hoggat VE. Fibonacci and Lucas Numbers, Houghton-Mifflin, Palo Alto, California, 1969.
- Стахов А.П. Формула Кассини // «Академия Тринитаризма», М., Эл № 77-6567, публ.12542, 01.11.2005 http://www.trinitas.ru/rus/doc/0232/004a/02320030.htm
- Stakhov AP. A generalization of the Fibonacci Q-matrix. Доклады Академии наук Украины, 1999, No 9: 46-49.
- Stakhov A.P., Massingua V., Sluchenkova A.A. Introduction into Fibonacci Coding and Cryptography». Харьков, Изд-во «Основа» Харьковского университета, 1999.
- Stakhov AP. Fibonacci matrices, a generalization of the «Cassini formula» and a new coding theory. Chaos, Solitons & Fractals (in press) http://www.trinitas.ru/rus/doc/0232/004a/02321039.htm
- Стахов А.П., Ткаченко И.С. Гиперболическая тригонометрия Фибоначчи. Доклады Академии наук УССР, том 208, № 7, 1993 г.
- Stakhov A.P. Hyperbolic Fibonacci and Lucas Functions: a New Mathematics for Living Nature. Vinnitsa, ITI, 2003.
- Стахов А.П. Новая математика для живой природы: Гиперболические функции Фибоначчи и Люка». Винница, Изд-во «ITI», 2003.
- Stakhov A, Rozin B. On a new class of hyperbolic function. Chaos, Solitons & Fractals 2004, 23(2): 379-389.
- Stakhov AP. The «golden» matrices and a new kind of cryptography. Chaos, Solitons & Fractals (in press).
А.П. Стахов, Матричный подход в «теории Золотого Сечения» и «золотые» геноматрицы Сергея Петухова // «Академия Тринитаризма», М.,
|
|