Abstract

The new continuous functions for the Fibonacci and Lucas p-numbers using Binet formulas are introduced. The article is of a fundamental interest for Fibonacci numbers theory and theoretical physics.

1. New results in Fibonacci number theory

Modern science, particularly physics [1-13], widely applies the recurring series of the Fibonacci numbers F(n)

(1)

and the recurring series of the Lucas numbers L(n)

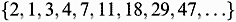
(2)

which result from application of the following recurrence relations:

(3)

(4)

(5)

(6)

The ratio of the adjacent numbers in the Fibonacci series (1) and Lucas series (2) tends toward at the irrational numbercalled the Golden Proportion (Golden Mean) [14—16].

In the 19th century the French mathematician Binet devised two remarkable analytical formulas for the Fibonacci and Lucas numbers [14—16]:

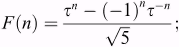
(7)

(8)

whereis the Golden Proportion and n = 0, ±1, ±2, ±3...

In recent years, researchers developed further the theory of the Golden Section and the Fibonacci numbers [17-30]. Hyperbolic Fibonacci and Lucas functions [21,24,26], which are extensions of Binet formulas for a continuous domain, have a strategic importance for the development of both mathematics and theoretical physics. In a previous article [28], the authors presented a new function of the second power called the Golden Shofar. The graph of this function reminds one of a horn, which is used to blow in the Yom Kippur (The Judgment Day).

The sinusoidal Fibonacci function [28] is a further development of a continuous approach to the Fibonacci numbers theory begun in a series of papers [21,24,26]. The definition of the function is

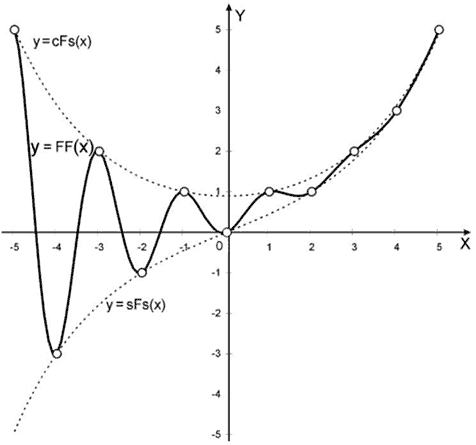
Fig. 1. The sinusoidal Fibonacci function.