|
|
|
Стахов А.П.
Аннотация
Похоже, что длившаяся несколько тысячелетий драматическая история Золотого Сечения в начале 21-го века — «Века Гармонии» — может закончиться большим триумфом для Золотого Сечения. Плитки Пенроуза, резонансная теория Солнечной системы (Молчанов, Бутусов), квазикристаллы (Шехтман), фуллерены (Крото и Смолли, Нобелевская Премия 1996 г.) стали только предвестниками этого триумфа. «Математика гармонии» (Стахов), гиперболические функции Фибоначчи и Люка (Стахов, Ткаченко, Розин), «геометрия Боднара», «Закон структурной гармонии систем» (Сороко), «теория E-infinity» (Эль Нашие), матрицы Фибоначчи и «золотые» квадратные матрицы (Стахов) и, наконец, «золотые» геноматрицы (Петухов) – вот далеко не полный перечень современных научных открытий, основанных на Золотом Сечении. Эти открытия дают основание высказать предположение, что Золотое Сечение является некоторым «метафизическим» знанием, «проточислом», «универсальным кодом Природы», который может стать основой для дальнейшего развития науки, в частности, математики, теоретической физики, генетики, компьютерной науки.
В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем. | |
Иоганн Кеплер
|
Содержание
- Введение
- История «золотого сечения»
- Некоторые открытия и теории современной науки, связанные с «золотым сечением»
- «Математика гармонии» как новая «метафизическая» теория современной математики
- Метафизические аспекты матричного анализа генетического кодирования и золотое сечение
- Заключение
1. Введение
В марте 2006 г. издательство «Бином» (Москва) выпустило в свет научный сборник «Метафизика. Век XXI» [1]. Составителем и редактором сборника является известный российский физик-теоретик проф. Ю.С. Владимиров (кафедра теоретической физики Московского университета).

Научный сборник «Метафизика. Век XXI» (Москва, Бином, 2006)
Сборник начинается с «Предисловия редактора», в котором дается детальный анализ статей, помещенных в сборнике. Всего в сборник включено 13 статей, которые сгруппированы в трех частях.
Часть 1. Общие вопросы метафизики
А.П. Огурцов. Судьба метафизики в век физики
В.Д. Захаров. Метафизика в борьбе с кантианством
Т.Е. Владимирова. Метафизические корни диалога культур
Р.Г. Баранцев. Семиодинамика как предтеча синергетики
Часть 2. Метафизика и исследовательские программы теоретической физики
Ю.С. Владимиров. Метафизический принцип фрактальности в физике
С.А. Векшенов, Ю.С. Владимиров. Об основаниях математики и физики
Ю.И. Кулаков. Теория физических структур – математическое основание фундаментальной физики
В.В. Кассандров. Алгебродинамика: квартернионный код вселенной
Д.Г. Павлов. Число и геометрия пространства-времени
Часть 3. Золотая пропорция в естествознании
А.П. Стахов. Золотое сечение, священная геометрия и математика гармонии
С.В. Петухов. Метафизические аспекты матричного анализа генетического кодирования и золотое сечение
А.С. Харитонов. «Золотая пропорция» как критерий универсального равновесия и оптимальной связности частей в целом
В.В. Очинский. К концепции золотой пропорции в естествознании
Главная задача сборника – изложить современные достижения «метафизики» и подчеркнуть ее фундаментальную, главенствующую роль в развитии современной науки.
Что же такое «метафизика»? Ответ на этот вопрос мы находим в статье А.П. Огурцова «Судьба метафизики в век физики» [2]. Как подчеркивается в статье, «традиционно под метафизикой понимается философское учение о предельных, сверхопытных основаниях, принципах и началах бытия» [2, c.20]. И далее: «Сам термин «метафизика» греческого происхождения. Он возник при систематизации произведений Аристотеля Андроником Родосским (1 в. до н.э.): после «Физики» Аристотеля должен был следовать трактат, посвященный исследованию «первых родов сущего». Это и было названо «метафизикой»,то, что следует после физики, то, что посвящено выявлению принципов и оснований физики как учения о становящейся, изменчивой, подвижной природе. Сами эти принципы и основания должны быть устойчивыми, неизменными или, как сказали бы в 20-м веке, инвариантными. Мета-физика – это знание, стоящее над физикой, сверхфизическое, сверхопытное, неиндуктивное. Это означает, что метафизика с самого начала претендовала на привилегированное положение во всей совокупности знаний: она занимала приоритетное место «демиурга» во всей системе знаний» [2, с.21].
Из этого определения вытекает, что «метафизика» претендует на роль некоторой «сверх-науки», которая «вынуждена восходить за пределы научного опыта, не просто размышлять о нем, а конструировать свои принципы и выдвигать свои начала вне и над научным опытом, эксплицируя принципы научного опыта, но, не сводясь к нему, возвышаясь над ним, нередко придумывая за науку принципы систематизации всего бытия, искать принципы своего знания» [2, c.22].
Пожалуй, наиболее характерной особенностью сборника «Метафизика. Век XXI» является появление в нем статей, посвященных «золотому сечению». Причину такого внимания к «золотому сечению» со стороны теоретической физики проф. Владимиров в своем «Предисловии редактора» [3] объясняет следующим образом:
«Третья часть сборника посвящена осмыслению многочисленных примеров проявления «золотой пропорции» в искусстве, биологии и окружающей нас действительности. Однако, как это ни парадоксально, в современной теоретической физике «золотая пропорция» никак не отражена. Чтобы убедиться в этом, достаточно пролистать 10-томник теоретической физики Л.Л. Ландау и Е.М. Лифшица. Назрело время заполнить этот пробел в физике, тем более, что «золотая пропорция» тесно связана с метафизикой, с тринитарностью»[3, с. 3-18].
Таким образом, спустя несколько тысячелетий после открытия «золотого сечения» в современной теоретической физике возрождается интерес к «золотому сечению». И появление статей по «золотому сечению» в престижном научном сборнике, посвященному обсуждению проблем «метафизики», «стоящей над наукой», является отражением этого интереса. В этой связи возникают следующие вопросы:
1. Насколько правомерным является отнесение «золотого сечения» к категории «метафизических» идей, «стоящих над наукой»?
2. Какова роль «золотого сечения» в реформировании современной фундаментальной науки?
В статьях А.П. Стахова [4], С.В. Петухова [5], А.С. Харитонова [6] и В.В. Очинского [7], помещенных в сборнике, делается попытка осветить некоторые «метафизические аспекты» золотого сечения. Главная цель настоящей статьи – провести анализ золотого сечения с «метафизической» точки зрения, то есть показать фундаментальную роль золотого сечения в развитии современной науки.
2. История «золотого сечения»
2.1. «Золотое сечение» в греческой культуре
История «золотого сечения» уходит вглубь тысячелетий. Мощный импульс в развитии «золотого сечения» и его приложений дала греческая наука. В Древней Греции «золотое сечение» становится своеобразным «каноном» древнегреческой культуры, который пронизывает все сферы греческой культуры. Широко известно следующее высказывание Алексея Лосева, в котором удачно подчеркнута роль «золотого сечения» в греческой культуре:
«С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления — Золотого Сечения... Их (древних греков – А.С.) систему космических пропорций нередко в литературе изображают как курьезный результат безудержной и дикой фантазии. В такого рода объяснениях сквозит антинаучная беспомощность тех, кто это заявляет. Однако понять данный историко-эстетический феномен можно только в связи с целостным пониманием истории, то есть, используя диалектико-материалистическое представление о культуре и ища ответа в особенностях античного общественного бытия».
Следует отметить, что строгая геометрическая формулировка знаменитой «задачи о делении отрезка в крайнем и среднем отношении» (так в древности называлась задача о «золотом сечении») впервые дана в Началах Евклида. Там же, а именно в 13-й, то есть заключительной книге своих Начал, Евклид изложил теорию Платоновых тел, которая является существенным разделом геометрической теории «золотого сечения», так как два главных Платоновых тела, додекаэдр и икосаэдр, основаны на «золотом сечении». Кстати, этот факт, то есть размещение теории правильных многогранников, лежащих в основе космологии Платона, в заключительной (то есть как бы самой главной) книге Начал Евклида, дало основание древнегреческому математику Проклу, который был комментатором Евклида, выдвинуть интересную гипотезу об истинных целях, которые преследовал Евклид, создавая свои Начала. Согласно Проклу, Евклид создавал Начала не с целью изложения геометрии как таковой, а чтобы дать полную систематизированную теорию построения «идеальных» фигур, в частности пяти Платоновых тел, попутно осветив некоторые новейшие достижения математики!
2.2. Числа Фибоначчи
В 13 в. при изучении задачи о «размножении кроликов» выдающийся итальянский математик Фибоначчи открыл рекуррентную формулу:
| F(n) = F(n-1) + F(n-2), | (1) |
которая при начальных условиях F(1) = F(2) = 1 порождает знаменитые числа Фибоначчи F(n): 1, 1, 2, 3, 5, 8, 13, 21,..., получившие в дальнейшем широкую известность, особенно в ботанике, где они выражают так называемый «закон филлотаксиса», которому подчиняются ростовые процессы многих ботанических структур [8-10].
Историческое значение формулы (1) состоит в том, что это была первая в истории математики рекуррентная формула, к которой в своих истоках восходит метод рекуррентных соотношений, ставший в дальнейшем одним из наиболее мощных методов решения комбинаторных задач. Историческое значение «задачи о кроликах» состоит в том, что эта задача дает начало «теории биологических популяций», описываемой с помощью рекуррентных соотношений.
2.3. «Божественная пропорция» Луки Пачоли
В эпоху Возрождения огромный вклад в развитие «Теории Золотого Сечения» внес знаменитый итальянский математик и ученый монах Лука Пачоли (1445-1517), друг и советник Леонардо да Винчи. Лука Пачоли пишет первое в истории науки математическое сочинение о Золотой Пропорции, названное им «De Divina Proportione» («О Божественной Пропорции») и опубликованное в 1509 г. Книга состоит из трех частей: в первой части излагаются свойства золотого сечения, вторая часть посвящена правильным многогранникам, третья – приложениям золотого сечения в архитектуре. В этой книге Пачоли, апеллируя к «Государству», «Законам», «Тимею» Платона, последовательно выводит 12 (!) различных свойств золотого сечения. Характеризуя эти свойства, Пачоли пользуется весьма сильными эпитетами: «исключительное», «превосходнейшее», «замечательное», «почти сверхъестественное» и т.п. Раскрывая данную пропорцию в качестве универсального отношения, выражающего и в природе и в искусстве совершенство красоты, он называет ее «божественной» и склонен рассматривать ее как «орудие мышления», «эстетический канон», «как принцип мира и природы». Эта книга является одним из первых математических сочинений, в котором христианская доктрина о Боге как творце Вселенной получает научное обоснование. Пачоли называет золотое сечение «божественным» и выделяет ряд свойств золотой пропорции, которые, по его мнению, присущи самому Богу.
2.4. Додекаэдро-икосаэдрическая доктрина
Среди пяти Платоновых тел особую роль играют икосаэдр и додекаэдр.
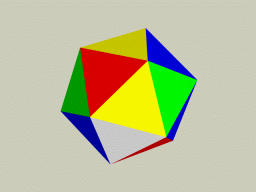
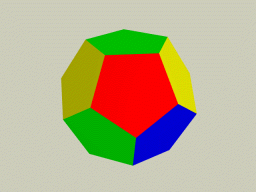
Икосаэдр и додекаэдр
Роль этих совершенных геометрических фигур, основанных на «золотом сечении», в развитии науки настолько велика, что правомерно говорить о том, что в трудах Платона возникла «икосаэдро-додекаэдрическая доктрина», которая «красной нитью» проходит через всю науку. Еще Сократ высказал предположение, что Земля имеет форму додекаэдра. Эта идея была затем развита в работах Бимона, Пуанкаре и Кислицина и привела к возникновению весьма оригинальных теорий формы Земли, имеющих важные практические приложения в геологии. В 17 в. Иоганн Кеплер, используя «Тела Платона» построил оригинальную геометрическую модель Солнечной Системы («Космический Кубок» Кеплера).
2.5. Вклад Кеплера в теорию Золотого Сечения
Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным приверженцем Золотого Сечения, Платоновых тел и Пифагорейской доктрины о числовой гармонии Мироздания. Свое восхищение «золотым сечением» Кеплер выразил в словах, которые взяты эпиграфом к настоящей статье.
Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:
![]()
в пределе стремится к золотой пропорции, то есть
![]()
2.6. Формула Кассини
В 17-м веке числа Фибоначчи привлекают внимание многих знаменитых ученых. Именно в этот период современник Кеплера, известный астроном Джованни Кассини (1625-1712) доказывает замечательное тождество, связывающее три соседних числа Фибоначчи:
| Fn-1 Fn+1 — |
(2) |
Формула (2) называется формулой Кассини. Эта удивительная формула вызывает благоговейный трепет, если представить себе, что она справедлива для любого значения n = 0, ± 1, ± 2, ± 3, …, и истинное эстетическое наслаждение, потому что чередование +1 и –1 в указанном выше математическом выражении при последовательном прохождении всех чисел Фибоначчи от -Ґ до +Ґ вызывает неосознанное чувство ритма и гармонии.
2.7. Вклад Люка в теорию Золотого Сечения
Начиная с 19 в., математические работы, посвященные свойствам чисел Фибоначчи, по остроумному выражению одного математика «начали размножаться как фибоначчиевые кролики». Лидером этих исследований в 19-м веке стал французский математик Люка (1842-1891). Заслуга Люка перед теорией чисел Фибоначчи состоит в том, что он впервые ввел в широкое употребление само название числа Фибоначчи и кроме того ввел в рассмотрение так называемые обобщенные числа Фибоначчи, описываемые следующей рекуррентной формулой:
| G(n) = G(n-1) + G(n-2). | (3) |
В зависимости от начальных членов G(1), G(2) рекуррентная формула (3) порождает бесконечное количество числовых последовательностей, подобных классическим числам Фибоначчи. Из всех возможных последовательностей, порождаемых (3), наибольшее применение получили две числовые последовательности – числа Фибоначчи F(n): 1, 1, 2, 3, 5, 8, 13, 21,... и так называемые числа Люка L(n): 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199,....
2.8. Формулы Бине
В 19-м веке было сделано одно из наиболее важных математических открытий в области «Теории Золотого Сечения», а именно, открыты две математические формулы, связывающие золотую пропорцию t с числами Фибоначчи и Люка:
| (4) |
| (5) |
где n = 0, ± 1, ± 2, ± 3, ….
Эти формулы широко известны и называются формулами Бине в честь французского математика 19-го века Жака Филлипа Мари Бине (1786 — 1856), который первым вывел эти формулы.
Исследования Фибоначчи, Пачоли, Кеплера, Люка и Бине стали стартовой площадкой для исследований российского математика Николая Воробьева, который своей замечательной брошюрой [8], первое издание которой относится к 1961 г., привлек внимание научной общественности 20-го века к числам Фибоначчи. В 1963 г. группа американских математиков организовала Фибоначчи-ассоциация, которая поставила своей главной целью исследование математических свойств чисел Фибоначчи и их приложений в различных сферах науки и искусства.
2.9. Икосаэдр как главный геометрический объект математики
Имя немецкого математика Феликса Клейна широко известно в математических кругах. В течении многих лет он возглавил математический институт Геттингенского университета, который на протяжении первой четверти 20-го века был признанным мировым математическим центром. Основные работы Клейна посвящены неевклидовой геометрии, теории непрерывных групп, теории алгебраических уравнений, теории эллиптических функций, теории автоморфных функций. Свои идеи в области геометрии Клейн изложил в работе «Сравнительное рассмотрение новых геометрических исследований» (1872), известной под названием Эрлангенская программа.
Кроме «Эрлангенской программы» и других выдающихся математических достижений, гениальность Феликса Клейна проявилась также в том, что более 100 лет назад он сумел предсказать выдающуюся роль Платоновых тел, в частности, икосаэдра, в будущем развитии науки, в частности, математики. В 1884 г. Феликс Клейн опубликовал книгу «Лекции об икосаэдре и решении уравнений пятой степени» [11], посвященную геометрической теории икосаэдра.
Согласно Ф. Клейну, ткань математики широко и свободно разбегается листами отдельных теорий. Но есть объекты, в которых сходятся несколько листов, — своеобразные точки ветвления. Их геометрия связывает листы и позволяет охватить общематематический смысл разных теорий. Именно таким математическим объектом, по мнению Клейна, является икосаэдр. Клейн трактует икосаэдр как математический объект, из которого расходятся ветви пяти математических теорий: геометрия, теория Галуа, теория групп, теория инвариантов и дифференциальные уравнения.
Таким образом, главная идея Клейна чрезвычайно проста: каждый уникальный геометрический объект так или иначе связан со свойствами икосаэдра.
Таким образом, еще в 19-м веке гениальная интуиция Феликса Клейна привела его к мысли о том, что одна из древнейших геометрических фигур – икосаэдр – является главной геометрической фигурой математики. Тем самым Клейн в 19 в. вдохнул новую жизнь в развитие «додекаэдро-икосаэдрического представления» о структуре Вселенной, последователями которого были великие ученые и философы: Платон, построивший свою космологию на основе правильных многогранников, Евклид, посвятивший свои «Начала» изложению теории Платоновых тел, Иоганн Кеплер, использовавший Платоновы тела при создании своего Космического кубка, весьма оригинальной геометрической модели Солнечной системы.
3. Некоторые открытия и теории современной науки,
связанные с «золотым сечением»
3.1. Плитки Пенроуза
В античной науке была широко известна «проблема паркета», которая сводится к плотному заполнению плоскости геометрическими фигурами одного вида. Как известно, такое заполнение может быть осуществлено с помощью треугольников, квадратов и шестиугольников. С помощью пятиугольников (пентагонов) такое заполнение невозможно.


Проблема паркета
Рассмотрим еще раз внимательно правильный пятиугольник, называемый также пентагоном или пентаграммой, плоскую геометрическую фигуру, основанную на «золотом сечении».
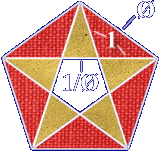
Правильный пятиугольник или пентагон
Как известно, после проведения в пентагоне диагоналей исходный пентагон может быть представлен как совокупность трех типов геометрических фигур. В центре находится новый пентагон, образуемый точками пересечения диагоналей. Остальная часть пентагона включает в себя пять равнобедренных треугольников, окрашенных в желтый цвет, и пять равнобедренных треугольников, окрашенных в красный цвет. Желтые треугольники являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют острые углы в 36° при вершине и острые углы в 72° при основании. Красные треугольники также являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют тупой угол в 108° при вершине и острые углы в 36° при основании.
А теперь соединим два желтых треугольника и два красных треугольника их основаниями. В результате мы получим два «золотых» ромба. Первый из них (желтый) имеет острый угол в 36° и тупой угол в 144°. Левый ромб будем называть тонким ромбом, а правый ромб – толстым ромбом.
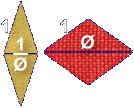
«Золотые» ромбы
Английский математик и физик Роджерс Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета, который был назван плитками Пенроуза. Плитки Пенроуза представляют собой комбинацию толстых и тонких ромбов.

Плитки Пенроуза
Важно подчеркнуть, что плитки Пенроуза имеют «пентагональную» симметрию или симметрию 5-го порядка, а отношение числа толстых ромбов к тонким стремится к золотой пропорции!
3.2. Квазикристаллы
12 ноября 1984 г. в небольшой статье, опубликованной в авторитетном журнале «Physical Review Letters» израильским физиком Даном Шехтманом, было предъявлено экспериментальное доказательство существования металлического сплава с исключительными свойствами. При исследовании методами электронной дифракции этот сплав проявил все признаки кристалла. Его дифракционная картина составлена из ярких и регулярно расположенных точек, совсем как у кристалла. Однако эта картина характеризуется наличием «икосаэдрической» или «пентангональной» симметрии, строго запрещенной в кристалле из геометрических соображений. Такие необычные сплавы были названы квазикристаллами. Менее чем за год были открыты многие другие сплавы подобного типа. Их было так много, что квазикристаллическое состояние оказалось намного более распространенным, чем это можно было бы представить.
Когда Дан Шехтман привел экспериментальное доказательство существования квазикристаллов, обладающих икосаэдрическиой симметрией, физики в поисках теоретического объяснения феномена квазикристаллов взяли за основу плитки Пенроуза, представляющие собой оригинальное решение «проблемы паркета», основанное на «золотых» ромбах [12].
В чем же состоит методологическое значение открытия квазикристаллов? Прежде всего, открытие квазикристаллов является моментом великого торжества «додекаэдро-икосаэдрической доктрины», которая пронизывает всю историю естествознания и является источником глубоких и полезных научных идей. Во-вторых, квазикристаллы разрушили традиционное представление о непреодолимом водоразделе между миром минералов, в котором «пентагональная» симметрия была запрещена, и миром живой природы, где «пентагональная» симметрия является одной из наиболее распространенных. И не следует забывать, что главной пропорцией икосаэдра является «золотая пропорция». И открытие квазикристаллов является еще одним научным подтверждением, что, возможно, именно «золотая пропорция», проявляющая себя как в мире живой природы, так и в мире минералов, является главной пропорцией Мироздания.
3.3. Фуллерены
Термином «фуллерены» называют замкнутые молекулы типа С60, С70, С76, С84, в которых все атомы углерода находятся на сферической или сфероидальной поверхности. В этих молекулах атомы углерода расположены в вершинах правильных шестиугольников или пятиугольников, которые покрывают поверхность сферы или сфероида. Центральное место среди фуллеренов занимает молекула С60, которая характеризуется наибольшей симметрией и как следствие наибольшей стабильностью. В этой молекуле, напоминающей покрышку футбольного мяча и имеющую структуру правильного усеченного икосаэдра, атомы углерода располагаются на сферической поверхности в вершинах 20 правильных шестиугольников и 12 правильных пятиугольников, так что каждый шестиугольник граничит с тремя шестиугольниками и тремя пятиугольниками, а каждый пятиугольник граничит с шестиугольниками.
«Фуллерены» по существу представляют собой «рукотворные» структуры, вытекающие из фундаментальных физических исследований. Впервые они были синтезированы в 1985 учеными Г. Крото и Р. Смолли (получившими в 1996 г. Нобелевскую премию за это открытие). Но в 1992 их неожиданно обнаружили в породах докембрийского периода, то есть фуллерены оказались не только «рукотворными», но и природными образованиями. Сейчас фуллерены интенсивно изучают в лабораториях разных стран, пытаясь установить условия их образования, структуру, свойства и возможные сферы применения.
Российские ученые А.В. Елецкий и Б.М. Смирнов в своей статье «Фуллерены», опубликованной в журнале «Успехи физических наук» (1993, том 163, №2), отмечают, что «фуллерены, существование которых было установлено в середине 80-х, а эффективная технология выделения которых была разработана в 1990 г., в настоящее время стали предметом интенсивных исследований десятков научных групп. За результатами этих исследований пристально наблюдают прикладные фирмы. Поскольку эта модификация углерода преподнесла ученым целый ряд сюрпризов, было бы неразумным обсуждать прогнозы и возможные последствия изучения фуллеренов в ближайшее десятилетие, но следует быть готовым к новым неожиданностям».
3.4. Резонансная теория Солнечной системы
Солнечная система представляет собой нелинейную колебательную систему, состоящую из слабо связанных нелинейных осцилляторов-планет. Советский математик А.М. Молчанов около 40 лет назад высказал гипотезу: любая нелинейная система (независимо от природы – механическая, химическая, биологическая или любая другая) в результате эволюции должна выходить на особый синхронный колебательный режим, при котором частоты объектов становятся равными, кратными или находятся в рациональных отношениях. Молчановым также доказан замечательный факт: при сколь угодно слабых взаимодействиях между элементами динамической системы их взаимное влияние в ходе эволюции приведет эту систему в синхронный режим. Проведенные Молчановым вычисления частот планет, в соответствии с высказанной им гипотезой, показали, что расчетные частоты отличаются от реально наблюдаемых не более чем на 1,5%. Это значит, что Солнечная система находится вблизи максимального резонансного состояния, которое является «неизбежным следствием ее эволюции и признаком ее эволюционной зрелости».
Дальнейшее развитие теория Молчанова получила в работе советского астронома К.П. Бутусова [13]. Бутусов сопоставил минимальные, средние и максимальные периоды обращений планет и периоды биений (разности частот обращений) для смежных планет со средним периодом обращения Земли, умноженным на число золотой пропорции в степени n, где n=0, ±1, ±2, ±3,.... При этом он получил ряд довольно точных совпадений, откуда Бутусов заключил, что «частоты обращения планет и разности частот обращений образуют спектр с интервалом, равным золотой пропорции»!
Эти необычное исследование привело также Бутусова к выводу о том, что «спектр гравитационных и акустических возмущений, создаваемых планетами, представляют собой консонантный аккорд, наиболее совершенный с эстетической точки зрения». Таким образом, в работе Бутусова идеи пифагорейцев и Кеплера о «музыке сфер» приобретают новое звучание и весьма реальное физическое содержание. В заключение своей статьи Бутусов делает замечание, что, видимо, только случайность не позволила Кеплеру, хорошо знакомому с золотым сечением и знавшему наизусть все параметры планетных орбит, открыть эту закономерность.
3.5. Фибоначчиевые резонансы генетического кода
Установление наукой ныне широко известного факта поразительной простоты основных принципов кодирования наследственной информации в живых организмах относится к числу важнейших открытий человечества. Эта простота заключается в том, что наследственная информация кодируется текстами из трехбуквенных слов – триплетов или кодонов, составленных на базе алфавита из четырех букв – азотистых оснований А (аденин), С (цитозин), G (гуанин), T (тимин). Данная система записи по существу едина для всего необозримого множества разнообразных живых организмов и называется генетическим кодом.
В 1990 г. французский исследователь Jean-Claude Perez, работавший в тот период научным сотрудником фирмы IBM, сделал весьма неожиданное открытие в области генетического кодирования. Он открыл математический закон, управляющий самоорганизацией оснований Т, С, А, G внутри ДНК. Он обнаружил, что последовательные множества нуклеотидов ДНК организованы в структуры дальнего порядка, называемые РЕЗОНАНСАМИ. Резонанс представляет собой особую пропорцию, обеспечивающую разделение ДНК в соответствии с числами Фибоначчи (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …).
Ключевая идея открытия Jean-Claude Perez, названного ДНК SUPRA-кодом, состоит в следующем. Рассмотрим любой отрезок генетического кода, состоящий из базисов типа Т, С, А, G, и пусть длина этого отрезка равна числу Фибоначчи, например, 144. Если число оснований типа Т в рассматриваемом отрезке ДНК равно 55 (число Фибоначчи) и суммарное число оснований типа А, С и G равно 89 (число Фибоначчи), то рассматриваемый отрезок генетического кода образует резонанс, то есть, резонанс есть пропорция между тремя соседними числами Фибоначчи (55-89-144). Открытие состоит в том, что каждая ДНК образует множество резонансов рассмотренного вида, то есть, как правило, отрезки генетического кода длиной, равной числу Фибоначчи Fn, разбиваются золотым сечением на множество оснований типа Т (число которых в рассматриваемом отрезке генетического кода равно Fn-2) и суммарное множество остальных оснований (число которых равно Fn-1). Если произвести систематическое исследование всех возможных «фибоначчиевых» отрезков генетического кода, тогда получим некоторое множество резонансов, называемое SUPRA-кодом ДНК.
Начиная с 1990 г., указанная закономерность была многократно проверена и подтверждена многими выдающимися биологами, в частности профессорами Montagnier and Chermann, исследовавших ДНК вируса СПИДа.
Например, генетический код b -цепи инсулина имеет следующий вид:
ATG-TTG-GTC-AAT-CAG-CAC-CTT-TGT-GGT-TCT-CAC-CTC-GTT-GAA-GCT
-TTG-TAC-CTT-GTT-TGC-GGT-GAA-CGT-GGT-TTC-TTC-TAC-ACT-CCT-AAG-
ACT
Генетический код инсулина
Заметим, что все основания типа Т в указанной последовательности окрашены красным цветом.
Проверка Закона Jean-Clode Perez на примере b -цепи молекулы инсулина привела к следующему результату. Общее число триплетов в b -цепи равно 30, то есть молекула содержит 90 оснований (89 — ближайшее число Фибоначчи). Если подсчитать число оснований Т в b -цепи, то оно равно 34 (34 — число Фибоначчи), а число остальных оснований равно 90-34 = 56 (55 — ближайшее число Фибоначчи). Таким образом, между основанием Т и остальными основаниями в b -цепи соблюдается следующая пропорция: 90-56-34. Эта пропорция очень близка к резонансу: 89-55-34. Из этого анализа вытекает, что Закон Jean-Clode Perez для b -цепи инсулина выполняется с весьма высокой для практики точностью.
Удивительное открытие Jean-Clode Perez позволяет сделать интересный вывод, касающийся аналогии между музыкой, поэзией, рыночными процессами («волны Эллиотта») и генетическим кодом. Несомненным является тот факт, что «гармония» этюдов Шопена, стихов Пушкина или «волн Элиотта», в которых «Золотое Сечение» наблюдается многократно, сходна «гармонии» генетического кода, в котором «фибоначчиевые резонансы», лежащие в основе ДНК SUPRA-кода, многократно наблюдаются как во всей молекуле ДНК, так и в каждой ее части.
3.6. Золотая пропорция в теории трансфинитных множеств Кантора и квантовой физике (E-infinity theory)
В последние годы наблюдается повышенный интерес теоретической физики к «золотому сечению». В работах английского физика египетского происхождения Мохаммеда Эль Нашие показана связь «золотого сечения» с квантовой физикой [14-19]. Разработанная им «теория E-infinity» вызвала широкий общественный резонанс.
Как известно, квантовая физика является одной из наиболее необычных физических теорий. Знаменитые опыты Юнга и Френеля экспериментально доказали корпускулярно-волновую природу света. В статье [19] Эль Нашие дискутирует с Лауреатом Нобелевской Премии английским физиком Gerard ‘t Hoofts относительно природы квантово-механического пространства-времени. Как известно, квантовая физика изменила Ньютоновское представление о природе геометрии пространстве-времени. Самая радикальная точка зрения, которая естественным образом вытекает из квантово-механических представлений, состоит в том, что пространство и время состоит из множества изолированных точек: при этом элементарные частицы должны находиться именно в этих точках, но не между ними. В соответствии с «квантовыми флуктуациями» все точки, в которых могут находиться «элементарные частицы», должны быть отделены друг от друга, по крайней мере, на расстояние, равное «постоянной Планка».
Ключевой вопрос, вытекающий из такого представления, состоит в следующем: как объяснить, как эти точки объединяются вместе, чтобы сформировать материю, которую мы называем пространством-временем? Простой ответ на этот вопрос дает «теория E-infinity», разработанная проф. Эль Нашие. Эта теория основывается на трансфинитных множествах, открытым немецким математиком Георгом Кантором еще в 19-м веке. Геометрия и топология трансфинитных множеств известна в современной математике под названием фракталов. Комбинация трансфинитных множеств и фракталов приводит к топологии, называемой «сумасбродной» или «дикой» (wild) топологией. Главная идея Эль Нашие состоит в использовании трансфинитных множеств Кантора в квантовой физике. Канторово множество – это абсолютно несвязанное множество точек, не имеющее никакой меры. Это означает, что, объединяя вместе все бесконечное множеств точек Канторового множества, мы получаем, что его длина всегда остается равной нулю. С другой стороны, доказано, что множество Кантора имеет размерность, отличную от нуля. Это размерность называется размерностью Хаусдорфа (Hausdorff). И здесь специалистов в области «золотого сечения» ожидает сюрприз в виде оригинальной математической теоремы, доказанной американским математиком Маудлином (Maudlin) [20]. В этой статье «доказана теорема, которая на первый взгляд кажется несколько парадоксальной, но воспринимается с захватывающим интересом. Эта теорема доказывает, что размерность Хаусдорфа (Hausdorff) для случайного множества Кантора ![]() , где
, где ![]() (»золотая пропорция»)».
(»золотая пропорция»)».
Число точек в множестве Кантора не только бесконечно. Оно содержит несчетное, бесконечно большое число точек. Другими словами, множество Кантора имеет кардинальность континуума. Главная идея Эль-Нашие и состоит в том, чтобы использовать трансфинитное множество Кантора в качестве модели квантово-механического пространства-времени. Эта модель и является тем способом, который позволяет соединить разрыв между дискретным и непрерывным.
А теорема Маудлина (Maudlin) [20] придает этой модели особый смысл, поскольку показывает, что «золотая пропорция» является некоторой фундаментальной константной квантово-механического пространства-времени.
Вторая ключевая идея теории Эль Нашие состоит в доказательстве связи фундаментального физического «опыта Юнга» с «золотой пропорцией». Рассмотрим рассуждения Эль Нашие, приводящие к такому заключению. Как известно «опыт Томаса Юнга» — это реальный физический эксперимент, который представляет собой квинтэссенцию всех «тайн» квантовой механики. Как известно, этот эксперимент убедительно показал корпускулярно-волновую природу света и привел к парадоксальному «корпускулярно-волновому дуализму», неразрешимому в рамках классической физики. Эль Нашие использует неразрешимость «корпускулярно-волнового дуализма», чтобы показать, что квантовое пространство-время может быть лучше описано с использованием бесконечно-мерной геометрии, основанной на трансфинитных множествах Кантора.
Напомним суть «опыта Юнга». В этом опыте узкий поток фотонов, электронов или других квантовых частиц направляется на экран с двумя узкими щелями 1 и 2, близко расположенными друг другу. Результат прохождения через щели фиксируется в виде интерференционной картины на другом экране, расположенном на определенном удалении от первого экрана. Именно эта интерференционная картина и доказывает корпускулярно-волновую природу квантовых частиц, то есть каждая элементарная частица (фотон или электрон) одновременно является и частицей и волной.
Обозначим через p1 вероятность квантовой частицы пройти через «щель» номер 1 и через p2 — вероятность пройти через «щель» номер 2. С другой стороны, мы можем принять, что волна, соответствующая квантовой частице, проходит через оба «щели» одновременно, так что вероятность прохождения волны через обе «щели» может быть выражена по правилу «пересечения»:
pД = p1 ґ p2.
С другой стороны, вероятность того, что частица пройдет через щель 1 или 2 задается «объединением» вероятностей p1 и p2, а именно pЕ. Если «корпускулярно-волновой дуализм» является неразрешимым в логическом смысле формальной системы, тогда pД должно быть равно pЕ. Однако, pЕ представляет собой возможную интерференцию и, следовательно, pЕ должно быть записано в виде:
pЕ = p1 + (- p2) = p1 — p2
Для положительного значения pЕ неразрешимость приводит к числовому уравнению для неразличимости между частицей и волной, а именно
pД = pЕ,
которое означает
| p1 — p2 = p1ґ p2 | (6) |
Если теперь воспользоваться условием нормализации для вероятностей p1 + p2 = 1 и представить p2 в виде:
p2 = 1 — p1
и подставит это выражение в (6), то мы получим следующее квадратное уравнение:
| p12 + p1 – 1 = 0. | (7) |
Положительный корень уравнения (7) ![]() есть величина, обратная «золотой пропорции». Из этих рассуждений вытекает, что для «опыта Юнга» характерны следующие величины вероятностей p1 и p2:
есть величина, обратная «золотой пропорции». Из этих рассуждений вытекает, что для «опыта Юнга» характерны следующие величины вероятностей p1 и p2:
p1 = b и p2 = 1 — b = b 2.
Появление «золотой пропорции» b = 0,618033989 в такой фундаментальной вероятностной ситуации является, по меньшей мере, удивительным. Вопрос заключается в том, какой механизм скрывается за этими необычными значениями вероятностей? Эль Нашие утверждает, что этот механизм надо искать в топологии Канторовского квантово-механического пространства-времени, которое он называет E-бесконечностью (E(Ґ)).
Такой необычный подход к интерпретации квантово-механического пространства-времени приводит Эль Нашие к ряду необычных открытий, касающихся теории элементарных частиц [14-19]. В частности в работах Эль Нашие показано, как, используя «золотую пропорцию», мы можем дойти до предсказания фундаментальных констант природы и вычислить спектр масс, а также, как оценить число бозонов Хайгса (Highs), которые предполагалось найти экспериментально, и т.д.
4. «Математика гармонии» как новая «метафизическая» теория современной математики
4.1. «Элементарная» и «высшая» математики
Впервые о «Математике Гармонии» было заявлено в докладе «The Golden Section and Modern Harmony Mathematics» [21], сделанном автором на 7-й Международной конференции «Числа Фибоначчи и их приложения» (Австрия, Грац, июль 1996 г.). Основы «Математики Гармонии» изложены в книгах и статьях автора [21-44]. Рассмотрим «Математику гармонии» с «метафизической» точки зрения. «Метафизический» подход предполагает ее рассмотрение как теории, затрагивающей фундамент математики, то есть теории, стоящей «над математикой». Что имеется ввиду? Обсуждая предмет математики, обычно принято делить ее на две условные части: (1) Элементарную математику и (2) Высшую математику. В русском языке определение «элементарная» к слову «математика» имеет некоторый уничижительный смысл. Речь идет о чем-то очень простом, «элементарном», «школьном», недостойном внимания серьезного ученого. Такая точка зрения на «элементарную математику» широко распространена среди некоторых математиков. Однако слово «elementary» имеет другой смысл в английском языке. Синонимом этого слова является слово «fundamental», что означает «основной», «базовый», «первичный», «существенный», «оригинальный». Напомним, что синонимом слова «elements» в английском языке является слово «fundamentals», что означает «начала», «основы». Именно такое значение имеет это слово, когда мы говорим «Euclidean Elements».
Мы будем использовать второе («английское») значение слова «элементарный». И тогда мы имеем право разбить математику на следующие части: (1) Фундаментальную математику (основы математики), содержащую некоторые общие, «метафизические» идеи, концепции и принципы и (2) Высшую математику, которая является развитием и приложением этих фундаментальных принципов и концепций.
Многие из «метафизических» открытий математической науки сделаны в античный период. К ним относятся:
- Позиционный принцип представления чисел (Вавилон)
- Тригонометрия, тригонометрические функции, число p (Вавилон, Египет)
- Начала и аксиомы геометрии (Вавилон, Египет, Древняя Греция)
- Золотое Сечение (Вавилон, Египет, Древняя Греция)
- Платоновы и Архимедовы тела (Египет, Древняя Греция)
- Конические сечения Аполлония (Древняя Греция)
- Натуральные числа и начала теории чисел (Древняя Греция)
- «Несоизмеримые отрезки» и иррациональные числа (Древняя Греция)
- Начала алгебры (Вавилон, Древняя Греция, Средняя Азия, Италия)
- Диофантовы уравнения (Древняя Греция)
В последующие периоды развития математики, вплоть до периода «высшей математики», начавшегося с открытия интегрального и дифференциального исчисления, в математике было сделано еще ряд «метафизических» открытий, к которым относятся:
- Десятичная система счисления (Индия)
- Числа Фибоначчи (Италия)
- Комбинаторика, биномиальные коэффициенты и треугольник Паскаля (Индия, Франция)
- Гиперболические функции (Италия)
- Логарифмы и число е (Шотландия)
4.1. Числа Фибоначчи в треугольнике Паскаля
Обнаружение связи чисел Фибоначчи (а, следовательно, и «золотого сечения») с «Треугольником Паскаля», который является одним из «стратегических» объектов математики и лежит в основе комбинаторного анализа, можно считать одним из важнейших открытий современной «теории чисел Фибоначчи». Исследование так называемых «диагональных сумм» треугольника Паскаля привело к обнаружению новых видов числовых последовательностей, названных р-числами Фибоначчи [22]. При заданном целом р=0, 1, 2, 3,... такие числовые последовательности задаются рекуррентной формулой:
Fp(n+1) = Fp(n)+Fp(n-p)
при следующих начальных условиях:
Fp(1) = Fp(2) =... = Fp(p+1) = 1.
В [22] выведена следующая формула, которая связывает р-числа Фибоначчи с биномиальными коэффициентами:
![]()
Заметим, что при р=0 эта формула сводится к широко известной формуле комбинаторного анализа:
![]() .
.
4.2. Обобщение задачи о «золотом сечении»
Еще одним математическим открытием современной «теории Золотого Сечения» является обобщение задачи о «золотом сечении» [22]. Зададимся целым неотрицательным числом р=0, 1, 2, 3,... и разделим отрезок AВ точкой C в следующей пропорции:
| (8) |
Решение задачи сводится к алгебраическому уравнению:
| xр+1 = xр + 1. | (9) |
Деление отрезка в отношении (8) названо золотым р-сечением на том основании, что при р=1 оно сводится к классическому «золотому сечению». Положительный корень t р уравнения (9) назван золотой р-пропорцией на том основании, что при р=1 она сводится к классической «золотой пропорцией».
Для золотой р-пропорции t р справедливо следующее математическое тождество:
| (10) |
Доказано [22], что отношение соседних р-чисел Фибоначчи Fp(n+1)/Fp(n) в пределе (n® Ґ) стремится к золотой р-пропорции t р. Это означает, что золотая р-пропорция выражает некоторые неизвестные нам ранее свойства треугольника Паскаля.
4.3. Обобщенный принцип Золотой Пропорции
Как известно, к разряду «метафизических» знаний, «стоящих над наукой», относятся ее «научные принципы», которые лежат в основе многих наук. К их числу относятся «Принцип дихотомии» и «Принцип золотого сечения», которые пришли к нам из античной науки [45].
«Принцип дихотомии» основывается на следующем простейшем тождестве, связывающем «двоичные числа»:
2n = 2n-1 + 2n-1,
где n=0, ±1, ±2, ±3, …. Для случая n=0 его можно записать в виде:
1 = 20 = 2 -1 + 2 -1
или
| (11) |
«Принцип золотого сечения» основывается на следующем тождестве, которое связывает степени «золотой пропорции»:
t n = t n-1 + t n-2,
где n=0, ±1, ±2, ±3, …. Для случая n=0 его можно записать в виде:
1 = t 0 = t -1 + t -2
или
| (12) |
Значение формул (11), (12) состоит в том, что они выражают разложение «Единицы» как универсальной модели «Целого» на простейшие составляющие. Принципы дихотомии и золотого сечения, основанные на (11), (12), являются своеобразным «метаязыком живой природы» и широко в ней используются [45]. В работе [6] показано, что «Принцип золотого сечения» есть основа универсального равновесия и оптимальной связности частей и целого.
В работе [38] предложен более общий принцип разложения «Целого» на простейшие составляющие, основанный на понятии золотой р-пропорциии и названный «Обобщенным принципом золотого сечения». Математически этот принцип выражается в виде следующего общего тождества:
| (13) |
которое сводится к тождествам (11) и (12) для частных случаев р=0 и р=1.
4.4. «Золотые» алгебраические уравнения и новый класс рекуррентных числовых последовательностей
«Золотое» алгебраическое уравнение (9) имеет р+1 корней x1, x2, x3, …, xp+1, первый из которых совпадает с золотой р-пропорцией, то есть, x1 = t p. Остальные корни могут быть комплексными и иррациональными. В работе [35] показано, что эти корни обладают уникальными математическими свойствами, что позволило открыть новый класс рекуррентных числовых последовательностей, названных р-числами Люка [36]. Доказано, что р-числа Люка могут быть выражены через корни x1, x2, x3, …, xp, xp+1 в виде:
| Lp (n) = (x1)n + (x2)n + … + (xр+1)n | (14) |
где n=0, ±1, ±2, ±3, …. Кроме того доказано [36], что р-числа Люка могут быть также заданы в виде следующей рекуррентной формулы:
Lp (n) = Lp (n-1) + Lp (n-р-1),
при следующих начальных условиях:
Lp (0) = р+1,
Lp (1) = Lp (2) =... = Lp (р) = 1,
где р=0, 1, 2, 3,....
Учитывая, что числа Lp (n) в формуле (14) всегда являются целыми числами, а корни x1, x2, x3, …, xp+1 являются иррациональными и комплексными числами, формула (14) представляет большой теоретико-числовой интерес.
В работе [34] найден класс «золотых» алгебраических уравнений n-й степени, имеющих общий корень t p:
| (15) |
где Fp(n) –р-числа Фибоначчи.
При р=1 и n=4 общее «золотое» алгебраическое уравнение (15) сводится к следующему уравнению
x4 = 3x + 2.
К этому уравнению пришел Лауреат Нобелевской Премии Ричард Фейнман при исследовании энергетических соотношений в молекуле бутадиена, ценного химического вещества, используемого при создании каучука. Исследования Ричарда Фейнмана позволяют высказать гипотезу о том, что «золотые» алгебраические уравнения (15), количество которых бесконечно, могут быть использованы при исследовании энергетических соотношений в молекулах других химических веществ.
4.5. Закон структурной гармонии систем (Э.М. Сороко)
Повышение интереса к проблеме гармонии и золотого сечения, что является одной из важнейших тенденций в развитии современной науки, не могло не привести к появлению оригинальных идей и открытий в современной философской науке. Одно из таких открытий было сделано белорусским философом Эдуардом Сороко, который выдвинул и развил в 80-е годы чрезвычайно интересную концепцию структурной гармонии систем [46]. Эта концепция и вытекающий из нее закон структурной гармонии систем, основанный на понятии «обобщенных золотых сечений», по праву можно считать одним из крупных философских достижений 20-го века. Главная идея Сороко состоит в том, чтобы рассмотреть реальные системы с «диалектической точки зрения». Как известно, всякий объект природы может быть представлен как диалектическое единство двух противоположных сторон A и B. Это диалектическая связь может быть выражена в следующем виде:
A + B = U (universum).
Это равенство является наиболее общей формой выражения так называемого закона сохранения. Здесь А и В различия внутри единства, логически непересекающиеся классы или состояния субстрата некоторого целого. Единственное условие: А и В должны измеряться одной и той же мерой, быть членами отношения, лежащего внутри единства. Примерами этого равенства могут быть вероятность и невероятность событий, масса и энергия, ядро атома и его оболочка, вещество и поле, анод и катод, животные и растения, духовное и материальное начала в системе ценностей, доход и расход и т.д.
Рассмотрим процесс самоорганизации системы. Он сводится к переходу системы в состояние «гармонического равновесия». Очевидно, что существует некоторое соотношение, пропорция между сторонами A и B диалектического противоречия в состоянии «гармонического равновесия». Исследуя это соотношение, Сороко пришел к неожиданому заключению, которое он назвал «Законом структурной гармонии систем»:
«Обобщенные золотые сечения суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоничное строение, стационарный режим существования, структурно-функциональную... устойчивость».
В чем же принципиальная особенность «Закона Сороко»? Начиная с Пифагора, ученые связывали понятие гармонии с единственной золотой пропорцией ![]() . «Закон Сороко» утверждает, что «гармоничное состояние» системы, соответствующее классической «золотой пропорции», не является единственным и что для одной и той же системы может существовать бесконечное количество «гармоничных» состояний, соответствующих «золотым р-пропорциям» t р.
. «Закон Сороко» утверждает, что «гармоничное состояние» системы, соответствующее классической «золотой пропорции», не является единственным и что для одной и той же системы может существовать бесконечное количество «гармоничных» состояний, соответствующих «золотым р-пропорциям» t р.
4.6. Новая теория гиперболических функций
Как известно, открытие неевклидовой или гиперболической геометрии, сделанное в начале 19-го века гениальным российским геометром Николаем Лобачевским, считается едва ли не самым важным математическим открытием 19-го века. До создания неевклидовой геометрии не было необходимости в доказательстве взаимодействия механики Ньютона и геометрии Евклида. Это считалось очевидным фактом. Такая необходимость возникла в конце 19-го — начале 20-го веков, когда в физике было накоплено много новых наблюдений и фактов, не укладывающихся в систему классической концепции пространства. Из исследований Максвелла по электродинамике, опытов Майкельсона по измерению скорости света, других научных данных непосредственно вытекал вопрос о соответствии евклидовой модели пространства свойствам реального физического пространства. Объяснение новых физических фактов, ставивших в тупик отношение физики с классической геометрией, дала теория относительности Эйнштейна, одним из главных результатов которой стал вывод о неевклидовом характере геометрии реального пространства. Теория относительности впервые показала, что пространство и время – единое целое, континуум, что свойства пространства и времени органически взаимосвязаны.
В 1908 г., то есть спустя три года после обнародования специальной теории относительности, немецкий математик Герман Минковский представил геометрическое обоснование специальной теории относительности, основанное на гиперболических функциях.
Именно с таких позиций необходимо оценивать значение нового класса гиперболических функций, гиперболических функций Фибоначчи и Люка, основанных на «золотой пропорции». Исходными для этих функций оказались формулы Бине (4), (5), разработанных французским математиком Бине в 19-м веке. Теория нового класса гиперболических функций разработана А.П. Стаховым, И.С. Ткаченко и Б.Н. Розиным [26, 30, 31, 33]. Это открытие имеет революционное значение для развития современной математики и теоретической физики. Можно прогнозировать разработку на их основе «золотой» гиперболической геометрии, которая является развитием геометрии Лобачевского и «четырехмерного мира Минковского».
4.7. Новая геометрическая теория филлотаксиса (О.Я. Боднар)
Одним из вариантов «золотой» гиперболической геометрии является новая геометрическая теория филлотаксиса, разработанная украинским архитектором Олегом Боднаром [47]. Как известно, числа Фибоначчи и Люка составляют основу так называемого «закона филлотаксиса». Согласно этому закону число левых и правых спиралей на поверхности так называемых филлотаксисных объектов (сосновой шишки, ананаса, кактуса, головки подсолнечника и т.д.) описывается отношениями соседних чисел Фибоначчи.
Наблюдая филлотаксисные объекты в завершенном состоянии и наслаждаясь упорядоченным рисунком на его поверхности, мы всегда задаем себе вопрос: как в процессе роста на его поверхности формируется «фибоначчиевая» решетка? Эта проблема и составляет основу загадки филлотаксиса, которая представляет собой одну из наиболее интригующих загадок ботаники. Суть ее состоит в том, что у большинства видов биоформ в процессе роста происходит изменение порядков симметрии, причем это изменение симметрии осуществляется по закону «динамической симметрии»:
![]()
Объяснение механизма «динамической симметрии» было дано украинским исследователем Олегом Боднаром [46]. Боднару удалось построить оригинальную геометрическую модель филлотаксиса, в основе которой лежит предположение, что геометрия филлотаксисных объектов является гиперболической, а изменение порядков симметрии филлотаксисного объекта в процессе своего роста основывается на гиперболическом повороте, который является основным преобразующим движением гиперболической геометрии. При этом главная особенность «геометрии Боднара» состоит в том, что для описания математических соотношений новой геометрии он использовал так называемые «золотые» гиперболические функции, которые совпадают с гиперболическими функциями Фибоначчи и Люка [26, 30, 31, 33] с точностью до постоянных коэффициентов.
«Геометрия Боднара», основанная на «золотых» гиперболических функциях, является достаточно убедительным доказательством того факта, что наряду с гиперболической геометрией, основанной на классических гиперболических функциях («гиперболическая геометрия Лобачевского», «четырехмерный мир Минковского» и др.), в Природе наблюдается и другая гиперболическая геометрия, основанная на гиперболических функциях Фибоначчи и Люка. «Золотой» гиперболический мир, основанный на такой геометрии, существует объективно и независимо от нашего сознания. Этот мир с удивительной настойчивостью проявляет себя, прежде всего, в живой природе, в частности, в виде филлотаксисных спиралей, основанных на числах Фибоначчи, числах Люка и других числовых рекуррентных рядах подобного типа («Закон филлотаксиса»). Заметим, что гиперболические функции Фибоначчи и Люка, лежащие в основе явления филлотаксиса, не являются «выдумкой» математиков-фибоначчистов, а отражают важнейшую математическую закономерность, лежащую в основе геометрии живой природы.
Приходится только удивляться тому факту, что в течение многих столетий математики и физики-теоретики не уделяли должного внимания развитию математического аппарата для моделирования «золотого» гиперболического мира, который существует в реальной действительности. Возможно, причиной этого является тот факт, что «золотой» гиперболический мир имеет большее отношение к биологии и ботанике, чем к физике.
4.8. Новая теория измерения
Как известно, роль измерения в формировании и развитии точных наук чрезвычайно велика. «Наука начинается с тех пор, как начинают измерять. Точная наука немыслима без меры», — сказал гений российской науки Дмитрий Менделеев. Проследим теперь эволюцию понятия «измерения» в математике. Как известно, первой «теорией измерений» был свод правил, которыми пользовались древнеегипетские землемеры. От этого свода правил, как свидетельствуют древние греки, берет начало геометрия, обязанная своим появлением (и названием) задаче об «измерении земли». Наука об измерении развивается в античный период преимущественно как математическая теория. Именно в этот период происходит открытие несоизмеримых отрезков, формулировка «метода исчерпывания» Евдокса, к которому в своих истоках восходит теория чисел, интегральное и дифференциальное исчисление. Именно эти крупнейшие открытия античной математики, связанные с измерением, дают право болгарскому математику академику Л. Илиеву утверждать, что «на протяжении первой эпохи своего развития – от античности и вплоть до открытия дифференциального и интегрального исчисления – математика, исследуя в первую очередь проблемы измерения величин, создала геометрию Евклида и учение о числах» [48, с. 207].
Именно с таких позиций необходимо рассматривать алгоритмическую теорию измерения, изложенную автором в книге [22]. Наиболее неожиданным результатом этой теории являются «фибоначчиевые» алгоритмы измерения, основанные на р-числах Фибоначчи. В книге [22] показана связь алгоритмов измерения со способами позиционного представления чисел и задачей Фибоначчи о «размножении кроликов», которая является первой в истории науки задачей из области биологических популяций. Из этих рассуждений вытекает, что новая теория измерения [22], имеет отношение к трем «изоморфным» теориям: теории оптимальных алгоритмов измерения, новой теории позиционных систем счисления и новой математической теории биологических популяций.
4.9. Новая теория чисел
Как известно, «число» является одним из наиболее важных понятий математики, а теория чисел является одной из древнейших математических теорий. И если математику называют «царицей науки», то теорию чисел называют «царицей математики». Исторически первым возникло понятие натурального числа. Его введение было связано с практической потребностью в счете предметов. Выдающаяся роль понятия натурального числа в развитии математики выражена в следующих словах знаменитого математика Леопольда Кронекера (1823-1891): «Бог создал натуральные числа, все прочее – творение человека».
Считается, что «теория чисел» или «теоретическая арифметика» возникли в Древней Греции. Предмет «теории чисел» в значительной степени зависел от «геометрического определения» натурального числа, которое приведено в «Началах» Евклида. В этом определении под «натуральным числом» понималась сумма «Монад» или «Единиц»:
N = 1 + 1 + 1 + … + 1 (N раз).
Несмотря на предельную простоту такого определения, оно сыграло выдающуюся роль в математике и по существу определяет сам предмет «теории чисел», так как лежит в основе всех основных понятий классической «теории чисел», таких, как понятия простого и составного числа, а также в основе теории делимости и сравнений, которая традиционно считается важнейшим теоретико-числовым достижением «теории чисел».
Но кроме натуральных чисел в математике существуют действительные числа (рациональные и иррациональные). К сожалению, в математике отсутствует «конструктивная» теория действительных чисел, подобная «теории натуральных чисел».
Попытка преодолеть этот недостаток сделана автором в статье [32].
Новая теория действительных чисел основана на следующем позиционном представлении действительного числа А, основанном на золотой р-пропорции t p:
| (16) |
где ai — двоичная цифра i-го разряда позиционного представления (16), t p – золотая р-пропорция, которая является основанием системы счисления (16), ![]() - вес i-го разряда позиционного представления (16), i = 0, ± 1, ± 2, ± 3, ….
- вес i-го разряда позиционного представления (16), i = 0, ± 1, ± 2, ± 3, ….
В книге [24] позиционное представление (16) названо кодом золотой р-пропорции.
Отметим, что выражение (16) задает бесконечное число «двоичных» (то есть использующих цифры 0 и 1) позиционных представлений, так каждому р (р=0, 1, 2, 3, …) соответствует свое позиционное представление (16). В частности, при р=0 основание t р=2 и позиционное представление (16) сводится к классической двоичной системе счисления. При р=1 t р=![]() и позиционный способ (16) сводится к системе счисления Бергмана [49]:
и позиционный способ (16) сводится к системе счисления Бергмана [49]:
| (17) |
открытой американским математиком Джорджем Бергманом в 1957 г.
В чем же состоит теоретико-числовое значение новых позиционных представлений, задаваемых (16), (17). Главная особенность системы счисления Бергмана (17) и ее обобщения – кодов золотой р-пропорции (16) — заключается в их основаниях t (золотая пропорция) и t р (золотая р-пропорция). При р>0 все числа t р являются иррациональными числами. А это означает, что в данном случае мы имеем дело с позиционными представлениями необычного типа, которые были неизвестны до публикации статьи Бергмана (1957), – системами счисления с иррациональными основаниями. Система счисления Бергмана (16) и коды золотой р-пропорции (17) переворачивают наши традиционные представления о позиционных системах счисления, более того – традиционное соотношение между числами рациональными и иррациональными. В кодах золотой р-пропорции основанием, то есть началом счисления, являются некоторые иррациональные числа (типа золотой р-пропорции t р). С помощью таких представлений, частным случаем которых является система счисления Бергмана (17), можно представлять все другие числа, включая натуральные, дробные и иррациональные числа. И поэтому с достаточной смелостью можно утверждать, что система счисления Бергмана (17) и коды золотой р-пропорции (16), возможно, являются наиболее революционным открытием в теории позиционных систем счисления после изобретения вавилонянами позиционного принципа представления чисел и открытия индусами десятичной системы счисления.
4.10. «Золотое» представление натуральных чисел и «постоянная тонкой структуры»
Рассмотрим представление натуральных чисел N в системе счисления Бергмана:
| (18) |
Первый неожиданный результат, вытекающий из такого представления, состоит в том, что для любого натурального числа N сумма (18) всегда является конечной, то есть любое натуральное число N может быть представлено в виде конечного числа степеней «золотой пропорции». Этот же вывод справедлив и для представления натуральных чисел в коде золотой р-пропорции, задаваемом (16).
А теперь возвратимся на 2,5 тысячелетия назад и представим себе реакцию пифагорейцев на представление натуральных чисел в виде (18) Согласно главной доктрине пифагорейцев «Все есть число», в основе мироздания лежат натуральные числа и их отношения, так как любую вещь в природе можно выразить в виде отношения двух натуральных чисел (хотя после открытия «несоизмеримых отрезков» некоторое время это утверждение не соответствовало представлениям пифагорейцев). Но мы только что показали, что любое натуральное число может быть выражено через золотую пропорцию. Из этого рассуждения с необходимостью вытекает новая доктрина, которую пифагорейцы безоговорочно приняли, если бы знали о системе счисления Бергмана: «Все есть Золотая Пропорция!», так как любой объект математики может быть выражен через золотую пропорцию, которая, действительно, является некоторым «Универсальным числом Мироздания»!
Свойство систем счисления с иррациональными основаниями, заключающееся в возможности «абсолютно точного» представления любого натурального числа через степени «золотой пропорции», уже привлекло внимание представителей современной науки. С.В. Петухов в статье [5] так оценивает это свойство: «Это позволяет рассматривать золотое сечение как «проточисло», которое может сыграть важную роль в концепции, связанной с именами Д.Гильберта, Б.Рассела и др., о возможном в будущем теоретическом вычислении фундаментальных физических констант (типа постоянной тонкой структуры) через математические «проточисла», а не путем установления их приближенных значений в физических экспериментах». Самое любопытное, что это предсказание, касающееся «постоянной тонкой структуры», уже сбылось. В работе [18] с использованием своей теории E-infinty Эль Нашие доказал, что «постоянная тонкой структуры» a 0 выражается в виде следующей суммы степеней «золотой пропорции»:
a 0 = t 10 + t 5 +t 2 + (t)-2 = ![]() +
+![]() +
+ ![]() +
+![]() =
=
= 70 + 30![]() = 70 + 30ґ 2.23606798 = 137, 082037,
= 70 + 30ґ 2.23606798 = 137, 082037,
что с очень высокой точностью согласуется с экспериментальными данными.
4.11. Новое свойство натуральных чисел (Z-свойство)
Но главным результатом, вытекающим из представления натуральных чисел в виде (18), является доказательство нового свойства натуральных чисел, названного Z-свойством [32]. Для доказательства этого свойства используется следующее известное выражение, выражающую i-ю степень «золотой пропорции» t i через числа Фибоначчи Fi и числа Люка Li:
| (19) |
Если подставить в выражение (18) вместо t i его значение, задаваемое (19), то после несложных преобразований мы получим следующее выражение:
| 2N = A + B |
(20) |
где
| A = |
(21) |
| B = |
(22) |
Здесь коэффициенты ai – это двоичные коэффициенты 0 и 1, совпадающие с двоичными коэффициентами ai в выражении (18).
Рассмотрим теперь выражение (20). Это выражение весьма необычное. Действительно, сумма B чисел Фибоначчи с двоичными коэффициентами, задаваемая выражением (22), и сумма A для чисел Люка с двоичными коэффициентами, задаваемая выражением (21), всегда являются целыми числами. Но тогда согласно (20) удвоенное (т.е. четное) число 2N равно сумме целого числа A и произведения целого числа B на иррациональное число ![]() . И это согласно (20) должно выполняться для любого натурального числа N! Возникает вопрос: при каких условиях это возможно в общем случае? Ответ очень простой: это возможно только в том случае, если член A является четным числом, равным 2N, а член B в выражении (22) тождественно равен 0, то есть:
. И это согласно (20) должно выполняться для любого натурального числа N! Возникает вопрос: при каких условиях это возможно в общем случае? Ответ очень простой: это возможно только в том случае, если член A является четным числом, равным 2N, а член B в выражении (22) тождественно равен 0, то есть:
| A = |
(23) |
| B = |
(24) |
А теперь сравним выражения (18) и (22). Поскольку двоичные коэффициенты ai в этих выражениях совпадают, то это означает, что выражение (22) может быть получено из (18) путем простой подстановки числа Фибоначчи Fi вместо t i. Но согласно (24) сумма, полученная в результате такой подстановки тождественно равна 0 независимо от исходного натурального N! Заметим, что такое свойство справедливо только для натуральных чисел и названо в [31] Z-свойством натуральных чисел (от zero — ноль).
В работе [32] показано, что подобным свойством обладают все коды золотой р-пропорции, задаваемые (16).
Таким образом, спустя 2,5 тысячелетия после начала теоретического изучения натуральных чисел удалось обнаружить их новое свойство, которое возникает при их представлении в системе счисления Бергмана или коде золотой р-пропорции!
4.12. Новые компьютерные арифметики
Выражения (16), (17) являются основой для создания разнообразных компьютерных арифметик, описанных в работах [22, 24, 28, 29]. Эти арифметики затрагивают теоретические основы компьютеров и являются источником для развития новых компьютерных проектов. Особый интерес представляет собой «троичная зеркально-симметричная арифметика», разработанная в [29]. Эта арифметика может стать основой новых проектов отказоустойчивых процессоров и компьютеров.
4.13. Матрицы Фибоначчи и новая теория кодирования
В работе [27] разработана теория квадратных матриц специального типа, названных Qp-матрицами. Qp-матрица представляет собой квадратную (p+1)ґ(p+1)-матрицу (р=0, 1, 2, 3,...). Она содержит единичную pґp матрицу, ограниченную последней строкой, состоящей из нулей, и первым столбцом, который состоит из нулей, ограниченных единицами.
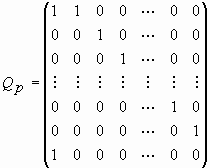 |
(25) |
Для случаев p = 0, 1, 2, 3, 4 Qp-матрицы имеют следующий вид соответственно:
Q0 = (1); ![]() ;
; 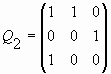 ;
;
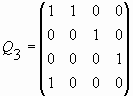 ;
; 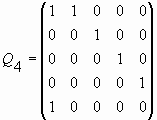 .
.
Qp-матрицы (25) обладают интересными свойствами. Так, например, Q3-матрица может быть получена из Q4-матрицы путем вычеркивания в последней последнего столбца и предпоследней строки. И это правило справедливо для всех соседних матриц Qp и Qp-1. Это означает, что все Qp-матрицы тесно связаны между собой, так как каждая Qp-матрица, с одной стороны, содержит все предыдущие Qp-матрицы и, с другой стороны, входит во все последующие. При этом Qp-1-матрица получается из Qp-матрицы путем вычеркивания последнего столбца и предпоследней строки. Поскольку на их пересечении находится 1, то из теории матриц вытекает, что детерминант Qp-1-матрицы отличается от детерминанта Qp-матрицы только знаком. Поскольку детерминант Q1-матрицы равен -1, то из этих рассуждений вытекает, что детерминант Qp-матрицы (25) равен:
| Det Qp = (-1)p. | (26) |
Для степеней матрицы Qp в [27] доказана следующая теорема.
Теорема. Для заданного целого р (р = 1, 2, 3, …) и заданного целого n (n = 0, ± 1, ± 2, ± 3, …) имеет место следующее выражение для n-й степени матрицы Qp:
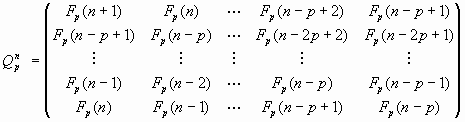 |
(27) |
Из теории матриц известно следующее свойство квадратной матрицы, возведенной в степень n:
| Det Qpn = (Det Qp)n. | (28) |
Учитывая (26), выражение (28) может быть записано в виде:
| Det Qp = (-1)pn, | (29) |
где p = 0, 1, 2, 3, …; n = 0, ± 1, ± 2, ± 3, ….
Заметим, что при р=1 Qp-матрица (25) и Qpn – матрица (27) принимают соответственно вид следующих хорошо известных выражений:
| (30) |
| (31) |
где F(n-1), F(n), F(n+1) - числа Фибоначчи.
Легко вычислить детерминант матрицы (31):
| Det Qn = Fn-1Fn+1 — |
(32) |
Сравнивая выражения (2) и (32), мы приходим к неожиданному заключению, что детерминант матрицы (31) совпадает с «формулой Кассини» (2), выведенной знаменитым астрономом Кассини еще в 17 в.! Этот результат наталкивает нас нам мысль, что формула (29) представляет собой сжатую запись формулы, подобной «формулы Кассини» (32), для всех Qpn – матриц (27). Этот результат сразу же приводит нас к неограниченному расширению исследований в области «теории чисел Фибоначчи» [8-10].
Таким образом, в работе [27] разработана теория квадратных матриц (25), (27), обладающих интересными математическими свойствами (26), (29). И теперь мы можем выразить лишь наше восхищение по поводу теории Qp-матриц, разработанной в [27], и могущества математики! Действительно, невозможно вообразить, что p-числа Фибоначчи, вытекающие из «Треугольника Паскаля», могут стать основой нового класса квадратных матриц, задаваемых выражениями (25) и (27) и обладающие уникальными математическими свойствами (26), (29).
В книге [28] изложена новая теория кодирования, основанная на умножении исходной («информационной») матрицы на «кодирующую матрицу» типа ![]() (кодирование) с последующим умножением полученной таким путем «кодовой матрицы» на декодирующую матрицу
(кодирование) с последующим умножением полученной таким путем «кодовой матрицы» на декодирующую матрицу ![]() , инверсную к
, инверсную к ![]() (декодирование). Показано, что «кодовая матрица», получаемая в результате кодирования, обладает тремя характерными свойствами: (1) детерминант «кодовой матрицы» равен по абсолютной величине детерминанту исходной («информационной») матрицы; (2) между элементами матрицы, находящимися в одной строке, устанавливается соотношение, близкое к золотой р-пропорции; (3) все элементы кодовой матрицы всегда являются целыми числами. Используя эти свойства, можно создать весьма эффективные процедуры обнаружения и исправления ошибок в кодовой матрице. Показано, что новый способ избыточного кодирования в 1000 и более раз превышает классические корректирующие коды по своей эффективности!
(декодирование). Показано, что «кодовая матрица», получаемая в результате кодирования, обладает тремя характерными свойствами: (1) детерминант «кодовой матрицы» равен по абсолютной величине детерминанту исходной («информационной») матрицы; (2) между элементами матрицы, находящимися в одной строке, устанавливается соотношение, близкое к золотой р-пропорции; (3) все элементы кодовой матрицы всегда являются целыми числами. Используя эти свойства, можно создать весьма эффективные процедуры обнаружения и исправления ошибок в кодовой матрице. Показано, что новый способ избыточного кодирования в 1000 и более раз превышает классические корректирующие коды по своей эффективности!
4.14. «Золотые» матрицы и новая теория криптографии
В работе [38] предложен новый класс квадратных матриц, названных «золотыми» матрицами. «Золотые» матрицы являются обобщением матрицы (31) и выражаются через гиперболические функции Фибоначчи в следующем виде:
| (33) |
| (34) |
где cFs(2x+1) и cFs(2x-1) – симметричные гиперболические косинусы Фибоначчи, а sFs(2x) – симметричный гиперболический синус Фибоначчи, введенные в [33].
Заметим, что матрицы (33), (34) являются функциями переменной x. Они имеют ряд необычных математических свойств. Например, для ![]() матрица (33) принимает следующую форму:
матрица (33) принимает следующую форму:
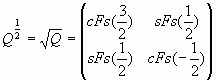 |
(35) |
Невозможно вообразить, что означает «корень квадратный из Q-матрицы», но именно такая «фибоначчивая фантазия» вытекает из выражения (36)!
Если мы теперь вычислим детерминанты матриц (33), (34), то мы придем к весьма необычным математическим тождествам для детерминантов этих матриц, которые справедливы для любого значения непрерывной переменной x:
| Det Q2x = 1 | (36) |
| Det Q2x+1 = - 1 | (37) |
Вновь обращаясь к «формуле Кассини», задаваемой (32), мы приходим к важному заключению, что необычные тождества (36), (37) являются ни чем иным, как обобщением «формулы Кассини» (32) на непрерывную область!
Можно предложить следующий метод шифрации-дешифрации, основанный на использовании «золотых» матриц (33), (34).
|
Шифрация |
Дешифрация |
|
Mґ Q2x = E1(x) |
E1(x)ґ Q-2x = M |
|
Mґ Q2x+1 = E2(x) |
E2(x)ґ Q-2x+1 = M |
Здесь M – исходная матрица размером 2ґ 2, представляющая собой исходное сообщение, подлежащее шифрации; E1(x), E2(x) – кодовые матрицы; Q2x, Q2x+1 – кодирующие матрицы, Q-2x, Q-2x+1- декодирующие матрицы, инверсные к Q2x, Q2x+1. Все они представляют собой «золотые» матрицы типа (33), (34). Мы можем использовать непрерывную переменную x в качестве криптографического ключа. Это означает, что в зависимости от значения x существует бесконечное число вариантов преобразования исходной матрицы M в кодовое (зашифрованное) сообщение E(x). Это обстоятельство может быть использовано в криптографии, то есть, рассматриваемый метод шифрации-дешифрации может рассматриваться как новый криптографический метод. Этот метод может быть эффективно использован для криптографической защиты так называемых «дискретных сигналов». Примерами использования таких сигналов могут быть цифровые системы связи (цифровая телефония, цифровое телевидение, цифровые измерительные системы и т.д.).
4.15. Место «Математики Гармонии» в системе математических теорий
Исчерпывающий ответ на поставленный вопрос дан в статье академика Ю.А. Митропольского [50], опубликованной на сайте «Академия Тринитаризма». Митропольский пишет: «Возникает вопрос, какое место в общей теории математики занимает созданная Стаховым Математика Гармонии? Мне представляется, что в последние столетия, как выразился когда-то Н.И. Лобачевский, «математики все свое внимание обратили на высшие части Аналитики, пренебрегая началами и не желая трудиться над обрабатыванием такого поля, которое они уже раз перешли и оставили за собою». В результате между «элементарной математикой», лежащей в основе современного математического образования, и «высшей математикой» образовался разрыв. И этот разрыв, как мне кажется, и заполняет Математика Гармонии, разработанная А.П. Стаховым. То есть «Математика Гармонии» — это большой теоретический вклад в развитие прежде всего «элементарной математики», и отсюда вытекает важное значение «Математики Гармонии» для математического образования».
5. Метафизические аспекты матричного анализа генетического кодирования и золотое сечение
5.1. Генетическое кодирование
С «метафизической» точки зрения большой интерес представляет статья [5], опубликованная известным российским ученым С.В. Петуховым, много лет плодотворно работающим на стыке математики и биологии. Основная идея С.В. Петухова состоит в представлении данных в системе генетического кодирования в виде матриц специального типа, названных им геноматрицами. Числовые геноматрицы порождаются из символьных геноматриц в результате замены символов генетических элементов их реальными количественными параметрами. Как подчеркивается в [5], «эта когнитивная форма представления уже привела к обнаружению новых феноменологических правил эволюции генетического кода, выявлению скрытых связей физико-химических параметров системы генетического кода с золотым сечением, обоснование новых подходов (в частности, хронобиологических) к вопросам генетического кодирования и пр. Оказывается, что загадочные наборы структур, реализованные природой в иерархической системе генетического кодирования, можно эвристическим образом сопоставить с семействами математических матриц, составленных из элементов данных структур. Язык матричного исчисления, являющийся одним из основных во всем современном математическом естествознании и компьютерной информатике, неожиданно выступает в роли языка результативного представления системы генетического кодирования. Это открывает дополнительную возможность взаимного обогащения различных «матричных» областей науки, а также усиливает роль матричного исчисления в математическом естествознании в целом».
Открытие генетического кода, общего для всех живых организмов – от бактерии до человека – привело к развитию информационной точке зрения на живые организмы. Как подчеркивается в [5], «с этой точки зрения организмы представляют собой информационные сущности. Они существуют потому, что получают наследственную информацию от своих предков и живут для того, чтобы передать свой информационный генетический код потомкам. При таком подходе все остальные физические и химические механизмы, представленные в живых организмах, можно трактовать как вспомогательные, способствующие реализации этой основной – информационной – задачи».
Основы языка наследственной информации поразительно просты. Для записи генетической информации в рибонуклеиновых кислотах (РНК) любых оргпнизмов используется «алфавит», состоящий из четырех «букв» или азотистых оснований: аденин (А), цитозин (С), гуанин (G), урацил (U) (в ДНК вместо урацила используется родственный ему тимин (Т)).
Генетическая информация, передаваемая молекулами наследственности (ДНК и РНК), определяет первичное строение белков живого организма. Каждый кодируемый белок представляет собой цепи из 20 видов аминокислот. Триплетом называется блок из трех соседних азотистых оснований. Из четырехбуквенного алфавита можно составить всего 43=64 триплетов. Генетический код называется вырожденным, поскольку 64 триплета кодируют всего 20 аминокислот. Если произвольная белковая цепь содержит n аминокислот, то соответствующая ему последовательность триплетов в молекуле ДНК содержит 3n азотистых оснований или, другими словами, задается 3n-плетом. Белковые цепи обычно содержат сотни аминокислот и соответственно задаются весьма длинными полиплетами.
5.2. Матричное представление генетических полиплетов
Основная идея С.В. Петухова состоит в том, чтобы представлять генетические полиплеты в матричном виде. Простейшей является квадратная матрица второго порядка Р, которая используется для представления системы из четырех «букв» генетического алфавита:
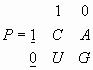 |
(38) |
Далее С.В. Петухов предлагает рассматривать семейство всех одинаковых по длине генетических полиплетов в виде соответствующего семейства матриц Р(n), представляющих собой тензорные (кронекеровы) степени исходной матрицы (38). В качестве примеров ниже построены матрицы Р(2) и Р(3):
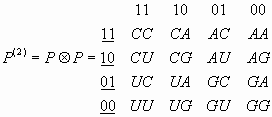 |
(39) |
 |
(40) |
Матрицы Р(n) названы геноматрицами. Данное семейство геноматриц Р(n) при достаточно большом n представляют всю систему генетических кодовых полиплетов, включая моноплеты генетического алфавита (38) и триплеты, кодирующие аминокислоты (40).
В каждом из четырех квадрантов геноматрицы Р(n) собраны все n-плеты, начинающиеся с одной буквы C, A, U, G. Если не обращать внимания на первую букву в n-плетах, то легко видеть, что квадрант матрицы Р(n) полностью воспроизводит матрицу Р(n-1) предыдущего поколения. С другой стороны, каждая матрица Р(n) образует квадрант матрицы Р(n+1) старшего поколения. Таким образом, геноматрица каждого нового поколения содержит в себе в скрытом виде информацию о всех предыдущих поколениях. Здесь уместно провести аналогию между геноматрицами Р(n) и Qp-матрицами (25), которые обладают аналогичным свойством, так как любая Qp-матрица (25) содержит в себе информацию о всех предыдущих матрицах Qp-1, Qp-2,..., Q1, Q0, но, с другой стороны, входит во все последующие матрицы Qp+1, Qp+2, Qp+3,....
5.3. Числовые геноматрицы
При замене в символьных матрицах каждого символа азотистых оснований на те или иные их количественные параметры получаются соответствующие числовые геноматрицы. Для образования таких количественных параметров С.В. Петухов предлагает воспользоваться числовыми значениями комплементарных водородных связей в азотистых основаниях генетического кода, «которые давно подозреваются на особую информационную значимость». Речь идет о двух и трех водородных связях (по которым C=G=3, A=U=2), соединяющих комплементарне пары азотистых оснований в молекулах наследственности, причем основания C и G число таких водородных связей равно 3, а для A и U равно 2. Ключевая идея Петухова состоит в том, чтобы заменить каждый полиплет во всех матрицах Р(n) произведением чисел водородных связей его азотистых оснований. При этом, например, триплет CGA в октетной матрице (40) заменяется на произведение 3ґ 3ґ 2=18. В результате такой замены можно получить, например, следующую октетную матрицу:
 |
(41) |
Легко обнаружить ряд интересных свойств числовой матрицы (41). Во первых, матрица (41) является симметричной относительно обеих диагоналей и поэтому названа бисимметричной. Во-вторых, сумма чисел в каждой ее строке и каждом ее столбце равна 53 = 125, а общая сумма чисел в матрице равна 103 = 1000. Оказывается, подобным свойством обладает любая числовая матрица ![]() , поскольку каждая такая матрица является бисимметричной, при этом сумма чисел в каждой ее строке и каждом ее столбце равна 5n, а общая сумма чисел в матрице равна 10n.
, поскольку каждая такая матрица является бисимметричной, при этом сумма чисел в каждой ее строке и каждом ее столбце равна 5n, а общая сумма чисел в матрице равна 10n.
5.4. «Золотые» геноматрицы
Рассмотрим числовую геноматрицу, соответствующую простейшей символьной геноматрице (38). Заменяя в ней азотистые основания C, A, U, G значениями их водородных связей (C=G=3, A=U=2), получим следующую числовую матрицу:
| (42) |
А теперь рассмотрим квадратную матрицу Фмульт, элементами которой являются числа ![]() («золотая пропорция») и
(«золотая пропорция») и ![]() :
:
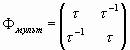 |
(43) |
Если теперь мы возведем матрицу (43) в квадрат, то найдем матрицу следующего вида:
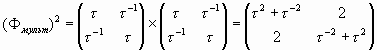 |
(44) |
А теперь вспомним формулу Бине для чисел Люка, задаваемую (5). Из этой формулы вытекает, что сумма t 2 + t -2 = L2 = 3. И тогда матрица (44) принимает вид матрицы (42), то есть,
| (45) |
Из этих простых рассуждений мы можем сделать вывод, что матрица (43) является как бы корнем квадратным из «золотой» матрицы (42), то есть, имеет место следующее соотношение:
| (Рмульт)1/2= Фмульт. | (46) |
Проведя подобные рассуждения для всех мультипликативных геноматриц типа ![]() , С.В. Петухов сделал серьезное научное открытие. Он обнаружил, что каждая из мультипликативных геноматриц типа
, С.В. Петухов сделал серьезное научное открытие. Он обнаружил, что каждая из мультипликативных геноматриц типа ![]() представляет вторую степень соответствующей «золотой» матрицы
представляет вторую степень соответствующей «золотой» матрицы ![]() , то есть:
, то есть:
![]() = (
= (![]() )2.
)2.
При этом Петуховым был найден очень простой алгоритм выписывания всех элементов «золотой» матрицы ![]() на основе исходной символьной матрицы Р(n). Для этого в исходной символьной матрице Р(n) каждый полиплет заменяется произведением следующих числовых значений для его букв: C=G=t, A=U=t -1. Например, триплет CGA в октетной матрице Р(3) заменяется на произведение t ґ t ґ t -1 = t. В качестве примера рассмотрим «золотую» матрицу
на основе исходной символьной матрицы Р(n). Для этого в исходной символьной матрице Р(n) каждый полиплет заменяется произведением следующих числовых значений для его букв: C=G=t, A=U=t -1. Например, триплет CGA в октетной матрице Р(3) заменяется на произведение t ґ t ґ t -1 = t. В качестве примера рассмотрим «золотую» матрицу ![]() , соответствующую символьной октетной матрице (40):
, соответствующую символьной октетной матрице (40):
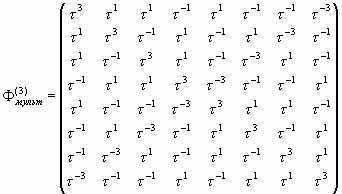 |
(47) |
Обнаружение связи золотого сечения с параметрами генетического кода позволило С.В. Петухову предложить новое – «матрично-генетическое» – определение золотого сечения: золотое сечение и его обратная величина (t и t -1) представляют собой единственные матричные элементы бисимметричной матрицы Ф, являющейся корнем квадратным из такой бисимметричной числовой матрицы Рмульт второго порядка, элементами которой являются генетические числа водородных связей (C=G=3, A=U=2) и которая имеет положительный детерминант.
Особого внимания заслуживает следующая цитата из статьи С.В. Петухова:
«Выдвинутое положение о матричном определении и матричной сущности золотого сечения дает эвристическую возможность рассмотреть весь этот материал на предмет его содержательной интерпретации с принципиально новой – матричной – точки зрения. Автор полагает, что многие реализации золотого сечения в живой и неживой природе связаны именно с матричной сущностью и матричным представлением золотого сечения. Математика золотых матриц – новая математическая веточка, изучающая, в частности, рекуррентные соотношения между рядами золотых матриц, а также моделирование с их помощью природных систем и процессов».
Как упоминалось, в 1999 г. автором настоящей статьи введен новый класс квадратных матриц, названных Qp-матрицами [27], а в работе [38] введен еще один класс квадратных матриц, названных «золотыми» матрицами. И хотя Qp-матрицы (25), (27) и «золотые» матрицы (33), (34) отличаются от «золотых» геноматриц С.В. Петухова, но, как упоминалось, они имеют с ними много общего с математической точки зрения. И поэтому автор считает своим долгом с энтузиазмом присоединиться к вышеуказанному высказыванию С.В. Петухова, в котором подчеркнута особая роль и плодотворность матричного подхода в теории золотого сечения.
6. Заключение
Итак, похоже, что длившаяся многие тысячелетия драматическая история «золотого сечения» может закончиться большим триумфом для «золотого сечения» в начале 21-го века — «Века Гармонии». Плитки Пенроуза, резонансная теория Солнечной системы, квазикристаллы Шехтмана, фуллерены (Нобелевская Премия 1996 г.) стали только предвестниками этого триумфа. Созданная автором «Математика Гармонии» [21] стала источником новых математических идей (обобщенные золотые сечения и «золотые» алгебраические уравнения, новые рекуррентные числовые последовательности – р-числа Фибоначчи и р-числа Люка, новая теория гиперболических функций, алгоритмическая теория измерения, системы счисления с иррациональными основаниями и новая теория действительных чисел, Z-свойство натуральных чисел, новые компьютерные арифметики и др.) [21-44]. Эти новые математические теории непосредственным образом влияют на развитие теоретического естествознания и компьютерной науки. Гиперболические функции Фибоначчи и Люка (Стахов, Ткаченко и Розин) и новая геометрическая теория филлотаксиса («геометрия Боднара») по существу дали теоретическое обоснование «золотому» гиперболическому миру, который существует независимо от нашего сознания и с удивительной настойчивостью проявляет в виде «фибоначчиевых» спиралей на поверхности сосновых шишек, кактусов, ананасов, головках подсолнечников и др. «Обобщенный принцип золотого сечения» [38] и «Закон структурной гармонии систем» Эдуарда Сороко [46] могут вызвать новую волну исследований в теоретическом естествознании и теории самоорганизующихся систем. Новые компьютерные арифметики, основанные на числах Фибоначчи и «золотом сечении» [22, 24, 28, 29], могут привести к новым компьютерным проектам («Компьютеры Фибоначчи»). Но заключительную точку в этой драматической истории ставят «теория E-infinity», созданная Эль Нашие [14-19] и «золотые» геноматрицы, введенные Сергеем Петуховым [5]. Исследования Эль Нашие показывают глубокую связь «золотого сечения» с квантовой физикой и открывают новые перспективы в развитии теории элементарных частиц. «Золотые» геноматрицы Петухова показывают, что «золотое сечение» лежит в основе генетического кода, то есть в основе всего живого на Земле. Матричный подход к «золотому сечению» оказался чрезвычайно плодотворным не только для генетического кодирования, но и стал источником создания новой теории кодирования [28] и новой теории криптографии [38].
Все вышеизложенное дает основание автору высказать предположение, что Золотое Сечение является некоторым «метафизическим знанием», «проточислом», «универсальным кодом Природы», который может стать основой для дальнейшего развития науки, в частности, математики, теоретической физики, генетики, компьютерной науки.
Литература
- Метафизика. Москва, Бином, 2006.
- Огурцов А.П. Судьба метафизики в век физики. Метафизика. Москва, Бином, 2006. — 20-44.
- Владимиров Ю.С. Предисловие редактора. Метафизика. Москва, Бином, 2006. — 3-18.
- Стахов А.П. Золотое сечение, священная геометрия и математика гармонии. Метафизика. Москва, Бином, 2006. — 174-215.
- Петухов С.В. Метафизические аспекты матричного анализа генетического кодирования и золотое сечение. Метафизика. Москва, Бином, 2006. — 216-250.
- Харитонов А.С. «Золотая пропорция» как критерий универсального равновесия и оптимальной связности частей в целом. Метафизика. Москва, Бином, 2006. — 251-255.
- Очинский В.В.. К концепции золотой пропорции в естествознании. Метафизика. Москва, Бином, 2006. — 256-284.
- Воробьев Н.Н. Числа Фибоначчи. Москва, Наука, 1978.
- Hoggat VE. Fibonacci and Lucas Numbers, Houghton-Mifflin, Palo Alto, California, 1969.
- Vajda S. Fibonacci & Lucas Numbers, and the Golden Section. Theory and Applications. Ellis Horwood limited, 1989.
- Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени: Пер. с нем. Москва, Наука, Главная редакция физико-математической литературы, 1989.
- Гратиа Д. Квазикристаллы. Москва, Успехи физических наук, 1988, том 156, вып. 2 — 347-363
- Бутусов К.П. Золотое сечение в Солнечной системе. – Астрономия и небесная механика. Серия «Проблемы исследования Вселенной», 1978, вып. 7. – 475-500.
- El Naschie MS On dimensions of Cantor set related systems. Chaos, Solitons & Fractals 1993, 3: 675-685
- El Nashie MS. Quantum mechanics and the possibility of a Cantorian space-time. Chaos, Solitons & Fractals 1992, 1: 485-487
- El Nashie MS. Is Quantum Space a Random Cantor Set with a Golden Mean Dimension at the Core? Chaos, Solitons & Fractals 1994, 4(2): 177-179
- El Naschie MS. The two-slit experiment as the foundation of E-infinity of high energy physics. Chaos, Solitons & Fractals 2005, 27: 509-514.
- El Naschie MS. Elementary number theory in superstrings, loop quantum mechanics, twistors and E-infinity high energy physics. Chaos, Solitons & Fractals 2006, 27(2): 297-330.
- El Naschie MS. ‘t Hooft ultimate building blocks and space-time as an infinite dimensional set of transfinite discrete points. Chaos, Solitons & Fractals 2005, 25: 521-524.
- Mauldin R.D. On the Hausdorff Dimension of Graphs and Random Recursive Objects. Dimensions and Entropies in Chaotic Systems. Proceedings of an International Workshop at the Pecos River Ranch, New Mexico, September 11-16, 1985. – 28-33.
- Stakhov A.P. The Golden Section and Modern Harmony Mathematics. Applications of Fibonacci Numbers, Volume 7, 1998. – 393-399.
- Стахов А.П. Введение в алгоритмическую теорию измерения. Москва, Советское Радио, 1977 г.
- Стахов А.П. Алгоритмическая теория измерения. Москва, Знание, серия «Математика и кибернетика», вып.6, 1979.
- Стахов А.П. Коды золотой пропорции. Москва, Радио и связь, 1984.
- Stakhov A.P. The Golden Section in the measurement theory. An International Journal «Computers & Mathematics with Applications», Volume 17, No 4-6, 1989. –
- Стахов А.П., Ткаченко И.С. Гиперболическая тригонометрия Фибоначчи. Доклады Академии наук УССР, том 208, № 7, 1993 г.
- Stakhov О.P. A generalization of the Fibonacci Q-matrix. – Доповіді Національної академії наук України. 1999, №9. 46-49.
- Stakhov A.P., Massingua V., Sluchenkova A.A. Introduction into Fibonacci Coding and Cryptography». Харьков, Изд-во «Основа» Харьковского университета, 1999.
- Stakhov AP. Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic. The Computer Journal 2002, Vol. 45, No. 2: 222-236.
- Stakhov A.P. Hyperbolic Fibonacci and Lucas Functions: a New Mathematics for Living Nature. Vinnitsa, ITI, 2003.
- Стахов А.П. Новая математика для живой природы: Гиперболические функции Фибоначчи и Люка». Винница, Изд-во «ITI», 2003.
- Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. Украинский математический журнал, том. 56, 2004. – 1143-1150.
- Stakhov A, Rozin B. On a new class of hyperbolic function. Chaos, Solitons & Fractals 2004, 23(2): 379-389.
- Stakhov A., Rozin B. The Golden Shofar. Chaos, Solitons & Fractals 2005, 26(3); 677-684.
- Stakhov A., Rozin B. The «golden» algebraic equations. Chaos, Solitons & Fractals 2005, 27 (5): 1415-1421.
- Stakhov A., Rozin B. Theory of Binet formulas for Fibonacci and Lucas p-numbers. Chaos, Solitons & Fractals 2005, 27 (5): 1162-1177.
- Stakhov A., Rozin B. The continuous functions for the Fibonacci and Lucas p-numbers. Chaos, Solitons & Fractals 2006, 28 (4): 1014-1025.
- Stakhov A. The Generalized Principle of the Golden Section and its applications in mathematics, science, and engineering. Chaos, Solitons & Fractals 2005, 26 (2): 263-289.
- Stakhov A. Fundamentals of a new kind of Mathematics based on the Golden Section. Chaos, Solitons & Fractals 2005, 27 (5): 1124-1146.
- Стахов А.П. Роль Золотого Сечения в современном математическом и общем образовании // «Академия Тринитаризма», М., Эл № 77-6567, публ.12374, 23.08.2005
- Стахов А.П. Сакральная геометрия и математика гармонии // «Академия Тринитаризма», М., Эл № 77-6567, публ.11176, 26.04.2004 (http://trinitas.ru/rus/doc/0202/010a/02020028.htm).
- Стахов А.П. Математика Гармонии как новое междисциплинарное направление современной науки // «Академия Тринитаризма», М., Эл № 77-6567, публ.12371, 19.08.2005 (http://www.trinitas.ru/rus/doc/0232/004a/02320001.htm)
- Стахов А.П., Розин Б.Н. «Золотые» гиперболические модели Природы // «Академия Тринитаризма», М., Эл № 77-6567, публ.12616, 22.11.2005 (http://www.trinitas.ru/rus/doc/0232/004a/02320034.htm)
- Стахов А.П. Троичный принцип Брусенцова, система счисления Бергмана и «золотая» троичная зеркально-симметричная арифметика // «Академия Тринитаризма», М., Эл № 77-6567, публ.12355, 15.08.2005 (http://www.trinitas.ru/rus/doc/0232/003a/02320001.htm)
- Шевелев И.Ш. Метаязык живой природы. – Кострома: Воскресенье 2000.
- Сороко Э.М. Структурная гармония систем. Минск, Наука и техника, 1984.
- Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. Львов, Изд-во «Свит», 1994.
- Илиев Л. Математика как наука о моделях. Успехи математических наук. 1972, том 27, вып. 2. – 206-220.
- Bergman G. A number system with an irrational base // Mathematics Magazine, 1957, No 31: 98-119.
- Митропольский Ю.А. Отзыв о научном направлении украинского ученого, доктора технических наук, профессора Алексея Петровича Стахова // «Академия Тринитаризма», М., Эл № 77-6567, публ.12452, 23.09.2005
Стахов А.П., Метафизика и Золотое Сечение // «Академия Тринитаризма», М.,
|
|