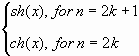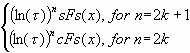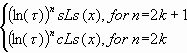|
|
|
Стахов А.П., Розин Б.Н.
Международный Клуб Золотого Сечения
6 McCreary Trail, Bolton, ON, Canada L7E8 2C
Аннотация
В статье приводится обзор новых математических моделей Природы основанных на Золотом Сечении. Основными из них являются гиперболические функции Фибоначчи и Люка и поверхность Золотой Шофар. Предлагается золотой гиперболический подход к моделированию Вселенной. Также рассматриваются обобщенные числа Фибоначчи, обобщенные золотые пропорции, «золотые» алгебраические уравнения, обобщенные формулы Бине, обобщенные числа Люка, непрерывные функций для обобщенных чисел Фибоначчи и Люка, матрицы Фибоначчи, «золотые» матрицы.
1. Введение
Одним из важнейших достижений современной науки является осознание того факта, что мир окружающей нас Природы является «гиперболическим». Как известно, приоритет в создании неевклидовой геометрии принадлежит русскому геометру Николаю Лобачевскому, который в 1827 г. предложил новую геометрическую систему, основанную на гиперболических функциях. В начале 20-го века в физике возникает потребность в использовании новых геометрических идей. Это было связано с созданием Эйнштейном специальной теории относительности (1905 г.). В 1908 г., то есть спустя три года после обнародования специальной теории относительности, немецкий математик Герман Минковский дал оригинальную геометрическую интерпретацию специальной теории относительности, основанную на гиперболических функциях.
Неожиданное развитие теория гиперболических функций получила в области математики, которая, на первый взгляд, никакого отношения к гиперболическим функциям не имеет. Речь идет о «теории чисел Фибоначчи», которая является активно развивающимся разделом современной математики [1-3]. В 1993 г. украинские математики А.П. Стахов и И.С. Ткаченко развили новый подход в теории гиперболических функций [4]. С использованием так называемых формул Бине в работах [4,5] предложен новый класс гиперболических функций, названных гиперболическими функциями Фибоначчи и Люка. Дальнейшее развитие эти идеи получили в работе [6], опубликованной в 2005 г. авторами настоящей статьи в международном журнале «Chaos, Solitons & Fractals». В этой работе введены так называемые симметричные гиперболические функции Фибоначчи и Люка. Развитием работы [6] является работа [7], в которой введена новая поверхность второго порядка, основанная на золотой пропорции и названная авторами «Золотой Шофар». Гиперболические функции Фибоначчи и Люка, а также поверхность «Золотой Шофар» являются наиболее яркими представителями «золотых» математических моделей, которые могут быть использованы для моделирования «гиперболических миров» Природы. Дальнейшее развитие таких моделей связано с понятиями обобщенных чисел Фибоначчи [8], обобщенных золотых пропорций [8], «золотых» алгебраических уравнений [9], обобщенных формул Бине [10], обобщенных чисел Люка [10], непрерывных функций для обобщенных функций Фибоначчи и Люка [11], матриц Фибоначчи [12] и «золотых» матриц [13]. Эти математические результаты были использованы в алгоритмической теории измерения [8, 14, 15], новой теории действительных чисел [16], математике гармонии [17-20], новых компьютерных арифметиках [8, 21-23], новой теории кодирования [24-25], при формулировке обобщенного принципа Золотого Сечения [13].
Настоящая статья носит обзорный характер и ставит своей целью в сжатой форме дать обзор «золотых» математических моделей для моделирования «гиперболических миров» Природы. Статья основана на работах [4-25].
2. Золотое Сечение, числа Фибоначчи & Люка и формулы Бине
Из «Начал» Евклида к нам пришла геометрическая задача «о делении отрезка в крайнем и среднем отношении». В современной науке эта задача известна как задача о «золотом сечении» геометрического отрезка [1-3]. Решение этой задачи сводится к решению следующего алгебраического уравнения:
| x2 = x + 1. | (1) |
Квадратное уравнение (1) имеет два корня. Его положительный корень ![]() называется золотой пропорцией, золотым средним или золотым отношением.
называется золотой пропорцией, золотым средним или золотым отношением.
Из (1) вытекает следующее замечательное свойство золотой пропорции:
| t n = t n-1 + t n-2 = t ґ t n-1> | (2) |
где n принимает значение из множества: 0, ± 1, ± 2, ± 3, ….
С золотой пропорцией тесно связаны две числовые последовательности – числа Фибоначчи
| Fn = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …}, | (3) |
которые задаются рекуррентным соотношением
| Fn = Fn-1 + Fn-2 | (4) |
при начальных условиях:
| F1 = F2 = 1, | (5) |
и числа Люка
| Ln = {1, 3, 4, 7, 11, 18, 29, 47, 76, …}, | (6) |
которые задаются рекуррентным соотношением
| Ln = Ln-1 + Ln-2 | (7) |
при начальных условиях:
| L1 = 1; L2 = 3 | (8) |
Числа Фибоначчи и Люка могут быть расширены в сторону отрицательных значений индекса n (Табл. 1).
Таблица 1. «Расширенные» числа Фибоначчи и Люка
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Fn |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
|
F-n |
0 |
1 |
-1 |
2 |
-3 |
5 |
-8 |
13 |
-21 |
34 |
-55 |
|
Ln |
2 |
1 |
3 |
4 |
7 |
11 |
18 |
29 |
47 |
76 |
123 |
|
L-n |
2 |
-1 |
3 |
-4 |
7 |
-11 |
18 |
-29 |
47 |
-76 |
123 |
Как следует из Табл.1, «расширенные» числа Фибоначчи и Люка обладают рядом интересных математических свойств. В частности, для нечетных n=2k+1 члены последовательностей Fn и F-n совпадают, то есть, F2k+1 = F-2k-1, а для четных n=2k они являются противоположными по знаку, то есть, F2k= -F-2k. Для чисел Люка Ln – все наоборот, то есть, L2k = L-2k; L2k+1 = -L-2k-1.
Пожалуй, наиболее важным результатом «Теории чисел Фибоначчи» [2, 3] являются формулы, выведенные в 19 в. известным французским математиком Бине. Эти формулы, называемые формулами Бине, связывают числа Фибоначчи Fn и числа Люка Ln с золотой пропорцией ![]() .
.
Формулы Бине для чисел Фибоначчи:
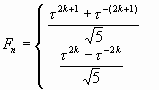 , , |
(9) |
Формулы Бине для чисел Люка:
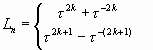 . . |
(10) |
где дискретная переменная k принимает значения из множества: 0, ± 1, ± 2, ± 3, ….
3. Гиперболические функции Фибоначчи и Люка
3.1. Подход Стахова и Ткаченко
Сравнение формул Бине (9), (10) с классическими гиперболическими функциями
| (11) |
| (12) |
показывает, что формулы Бине по своей структуре подобны гиперболическим функциям (11), (12). Это наблюдение и лежит в основе нового класса гиперболических функций, введенного в [4]. Для этого дискретная переменная k в формулах (9), (10) была заменена непрерывной переменной x, которая принимает значения из множества действительных чисел. В результате были получены следующие непрерывные функции, названные гиперболическими функциями Фибоначчи и Люка [4]:
Гиперболический синус Фибоначчи
| (13) |
Гиперболический косинус Фибоначчи
| (14) |
Гиперболический синус Люка
| (15) |
Гиперболический косинус Люка
| (16) |
Связь между числами Фибоначчи Fn и числами Люка Ln и гиперболическими функциями Фибоначчи и Люка (13)-(16) задается следующими соотношениями:
| sF(k) = F2k; cF(k) = F2k+1; sL(k) = L2k+1; cL(k) = L2k, | (17) |
где k= 0; ±1; ±2; ±3,....
Книга [5] посвящена изложению теории функций (13)-(16) и их приложениям в современной науке и математике. Наиболее важным из них является развитие нового («непрерывного») подхода к «Теории чисел Фибоначчи», основанного на соотношениях (17), которое связывает числа Фибоначчи и Люка с функциями (13)-(16). Суть этого подхода состоит в том, что «Теория чисел Фибоначчи» является вырожденным, «дискретным» случаем «теории гиперболических функций Фибоначчи и Люка», а любому «непрерывному» тождеству для гиперболических функций Фибоначчи и Люка соответствует некоторое «дискретное» тождество для чисел Фибоначчи и Люка и наоборот. Переход от «непрерывного» к «дискретному» тождеству осуществляется с использованием соотношений (17).
3.2. Симметричное представление гиперболических функций Фибоначчи
и Люка (подход Стахова и Розина)
Сравним теперь гиперболические функции Фибоначчи и Люка (13)–(16) с классическими гиперболическими функциями (11), (12). Легко увидеть, что, в отличие от классических гиперболических функций (11), (12), график косинуса Фибоначчи (14) асимметричен относительно оси y, а график синуса Люка (15) асимметричен относительно начала координат. Это ограничивает область эффективного приложения нового класса гиперболических функций, задаваемых (13)-(16).
Для устранения этого недостатка в работе [6] введен новый вид гиперболических функций Фибоначчи и Люка, названных симметричными гиперболическими функциями Фибоначчи и Люка.
Симметричный гиперболический синус Фибоначчи
| (18) |
Симметричный гиперболический косинус Фибоначчи
| (19) |
Симметричный гиперболический синус Люка
| (20) |
Симметричный гиперболический косинус Люка
| (21) |
Числа Фибоначчи и Люка связаны с введенными выше симметричными гиперболическими функциями Фибоначчи и Люка следующими соотношениями:
| (22) |
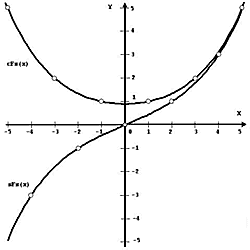
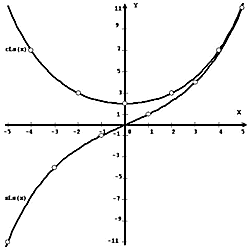
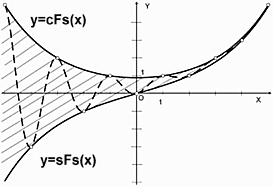
На Рис. 1 и 2 приведены графики введенных выше функций (18)-(21).
|
| ||||
|
Рисунок 1. Симметричные гиперболические функции Фибоначчи |
Рисунок 2. Симметричные гиперболические функции Люка |
Как следует из Рис. 1 и 2, графики функций (18)-(21) являются симметричными и подобны графикам классических гиперболических функций (11), (12). Заметим, что в точке x=0 симметричный косинус Фибоначчи cFs(x) принимает значение ![]() , а симметричный косинус Люка cLs(x) в этой точке принимает значение cLs(0) = 2. Важно подчеркнуть, то числа Фибоначчи Fn с четными индексами (n = 0, ± 2, ± 4, ± 6, …) «вписываются» в симметричный синус Фибоначчи sFs(x) в дискретных точках x = 0, ± 2, ± 4, ± 6, …, а числа Фибоначчи Fn с нечетными индексами (n = ± 1, ± 3, ± 5, …) «вписываются» в симметричный косинус Фибоначчи cFs(x) в дискретных точках x = ± 1, ± 3, ± 5 …. С другой стороны, числа Люка с четными индексами «вписываются» в симметричный косинус Люка cLs(x) в дискретных точках x = 0, ± 2, ± 4, ± 6 …, а числа Люка с нечетными индексами «вписываются» в симметричный синус Люка sLs(x) в дискретных точках x = ± 1, ± 3, ± 5 ….
, а симметричный косинус Люка cLs(x) в этой точке принимает значение cLs(0) = 2. Важно подчеркнуть, то числа Фибоначчи Fn с четными индексами (n = 0, ± 2, ± 4, ± 6, …) «вписываются» в симметричный синус Фибоначчи sFs(x) в дискретных точках x = 0, ± 2, ± 4, ± 6, …, а числа Фибоначчи Fn с нечетными индексами (n = ± 1, ± 3, ± 5, …) «вписываются» в симметричный косинус Фибоначчи cFs(x) в дискретных точках x = ± 1, ± 3, ± 5 …. С другой стороны, числа Люка с четными индексами «вписываются» в симметричный косинус Люка cLs(x) в дискретных точках x = 0, ± 2, ± 4, ± 6 …, а числа Люка с нечетными индексами «вписываются» в симметричный синус Люка sLs(x) в дискретных точках x = ± 1, ± 3, ± 5 ….
Введенные выше симметричные гиперболические функции Фибоначчи и Люка связаны с классическими гиперболическими функциями (11) и (12) следующими простыми соотношениями:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Симметричные гиперболические функции Фибоначчи и Люка связаны между собой следующими соотношениями:
![]() ;
; ![]() .
.
3.3. Рекуррентные свойства симметричных гиперболических функций Фибоначчи и Люка
Симметричные гиперболические функции Фибоначчи и Люка (18)-(21) являются «непрерывным» обобщением чисел Фибоначчи и Люка и, следовательно, они обладают рекуррентными свойствами. С другой стороны, они подобны классическим гиперболическим функциям (11) и (12) и, следовательно, они обладают гиперболическими свойствами.
Некоторые из «рекуррентных свойств» функций (18)-(21) приведены в Табл. 2.
Таблица 2. Рекуррентные свойства симметричных гиперболических функций Фибоначчи и Люка
|
Тождества для чисел Фибоначчи и Люка |
Тождества для симметричных гиперболических | |
|
Fn+2 = Fn+1+Fn |
sFs(x+2) = |
cFs(x+2) = |
|
Fn 2 — Fn+1 Fn-1 = |
[sFs(x)]2 — |
[cFs(x)]2 — sFs(x+1) sFs(x-1) = 1 |
|
Ln+2 = |
sLs(x+2) = cLs(x+1) + |
cLs(x+2) = sLs(x+1) + |
|
Ln2 — 2(-1)n = |
[sLs(x)]2 + 2 = |
[cLs(x)]2 — 2 = |
|
Fn+1 + Fn-1 = |
cFs(x+1) + cFs(x-1) = |
sFs(x+1) + sFs(x-1) = |
|
Fn + Ln = |
cFs(x) + sLs(x) = |
sFs(x)+ i>cLs(x) = |
Например, знаменитая «формула Кассини» [26]
| Fn 2 — Fn+1 Fn-1 = (-1)n+1, | (23) |
которая представляет собой одно из важнейших тождеств, связывающих три соседних числа Фибоначчи, в терминах симметричных гиперболических функций Фибоначчи представляется в виде двух «непрерывных» тождеств:
| [sFs(x)]2 — cFs(x+1) сFs(x-1) = -1 | (24) |
| [cFs(x)]2 — sFs(x+1) sFs(x-1) = 1, | (25) |
которые можно рассматривать как обобщение «формулы Кассини» (23) на непрерывную область.
3.4. Гиперболические свойства симметричных гиперболических функций Фибоначчи и Люка
Некоторые из «гиперболических свойств» симметричных гиперболических функций Фибоначчи и Люка приведены в Табл. 3.
Таблица 3. Гиперболические свойства симметричных гиперболических функций Фибоначчи и Люка
|
Классические гиперболические функции |
Симметричные гиперболические функции Фибоначчи |
Симметричные гиперболические функции Люка |
|
[ch(x)]2 – [sh(x)]2 = 1 |
[cFs(x)]2 — [sFs(x)]2 = |
[cLs(x)]2 — [sLs(x)]2 = 4 |
|
ch(x±y) = ch(x)ch(y) ± ± sh(x)sh(y) |
± sFs(x)sFs(y) |
2cLs(x±y) = cLs(x)cLs(y) ± ±sLs(x)sLs(y) |
|
sh(x±y) = sh(x)ch(y) ± ch(x)sh(y) |
± cFs(x)sFs(y) |
2sLs(x±y) = sLs(x)cLs(y) ± ± cLs(x)sLs(y) |
|
ch(2x) = [ch(x)]2 + [sh(x)]2 |
|
2cLs(2x) = [cLs(x)]2 + +[sLs(x)]2 |
|
sh(2x) = 2 sh(x)ch(x) |
|
sLs(2x) = sLs(x)cLs(x) |
|
[ch(x)](n) =
|
[cFs(x)](n) =
|
[cLs(x)](n)=
|
Например, наиболее важное тождество для классических гиперболических функций
| [ch(x)]2 – [sh(x)]2 = 1 | (26) |
выглядит следующим образом соответственно для симметричных гиперболических функций Фибоначчи и Люка:
| [cFs(x)]2 — [sFs(x)]2 = |
(27) |
| [cLs(x)]2 — [sLs(x)]2 = 4. | (28) |
Таким образом, введенные выше симметричные гиперболические функции полностью сохраняют свойства классических гиперболических функций (Табл. 3), но при этом обладают новыми («рекуррентными») свойствами, подобными свойствам чисел Фибоначчи и Люка (Табл. 2). При этом, в отличие от классических гиперболических функций, новые гиперболические функции имеют «дискретный аналог» в виде чисел Фибоначчи и Люка, с которыми согласно (22) указанные функции совпадают, когда непрерывная переменная x принимает «дискретные» значения: 0, ± 1, ± 2, ± 3, …. Заметим, что тождества (24)-(28), как и остальные тождества, приведенные в Табл. 2 и 3, подчеркивают фундаментальный характер введенных выше гиперболических функций Фибоначчи и Люка.
3.5. Геометрия Боднара
Как известно, числа Фибоначчи и Люка составляют основу так называемого «закона филлотаксиса» [27]. Согласно этому закону число левых и правых спиралей на поверхности так называемых филлотаксисных объектов (сосновой шишки, ананаса, кактуса, головки подсолнечника и т.д.) описывается отношениями соседних чисел Фибоначчи, то есть:
| (29) |
Эти отношения характеризуют «симметрию» филлотаксисного объекта. При этом, для каждого филлотаксисного объекта характерно свое отношение соседних чисел Фибоначчи из (29), которое называется порядком симметрии.
Наблюдая филлотаксисные объекты в завершенном состоянии и наслаждаясь упорядоченным рисунком на его поверхности, мы всегда задаем себе вопрос: как в процессе роста на его поверхности формируется фибоначчиевая решетка? Эта проблема и составляет основу загадки филлотаксиса, которая представляет собой одну из наиболее интригующих загадок ботаники. Суть ее состоит в том, что у большинства видов биоформ в процессе роста происходит изменение порядков симметрии, задаваемых (29). Известно, например, что головки подсолнечника, находящиеся на разных уровнях одного и того же стебля, имеют разные порядки симметрии: чем старше диск, тем выше порядок его симметрии. Это означает, что в процессе роста происходит закономерное изменение (возрастание) порядка симметрии и это изменение симметрии осуществляется по закону:
| (30) |
Изменение порядков симметрии филлотаксисных объектов в соответствии с (30) называется динамической симметрией [27]. Ряд ученых, исследовавших эту проблему, предполагают, что явление филлотаксиса имеет фундаментальное междисциплинарное значение. Например, по мнению В.И. Вернадского, проблема биологической симметрии является ключевой проблемой биологии.
Итак, явление динамической симметрии (30) обнаруживает свою особую роль в геометрической проблеме филлотаксиса. Напрашивается предположение, что за числовой закономерностью (30) кроются определенные геометрические законы, которые, возможно, и составляют суть секрета ростового механизма филлотаксиса и их раскрытие имело бы важное значение для разрешения проблемы филлотаксиса в целом. Эта фундаментальная проблема и была решена украинским исследователем Олегом Боднаром [27]. Боднару удалось построить оригинальную геометрическую теорию филлотаксиса, в основе которой лежит предположение, что геометрия филлотаксисных объектов является гиперболической, а изменение порядков симметрии филлотаксисного объекта в процессе своего роста основывается на гиперболическом повороте, который является основным преобразующим движением гиперболической геометрии. При этом главная особенность «геометрии Боднара» состоит в том, что для описания математических соотношений новой геометрии он использовал так называемые «золотые» гиперболические функции, которые совпадают с симметричными гиперболическими функциями Фибоначчи и Люка с точностью до постоянных коэффициентов.
Таким образом, «геометрия Боднара» является блестящим примером эффективного применения гиперболических функций Фибоначчи и Люка для моделирования процессов роста филлотаксисных объектов, то есть гиперболические функции Фибоначчи и Люка являются новыми и весьма эффективными математическими моделями той части биологического мира, который имеет отношение к явлению филлотаксиса.
4. Золотой Шофар
4.1. Квази-синусоидальная функция Фибоначчи
В математике [2,3] широко используется следующее представление формул Бине для чисел Фибоначчи:
| (31) |
где n= 0, ±1, ±2, ±3, ….
Сравнивая формулу Бине (31) с симметричными гиперболическими функциями Фибоначчи (18) и (19), можно увидеть, что непрерывным функциям t х и t -х в формулах (18) и (19) соответствуют дискретные последовательности t n и t -n в формуле (31), где n = 0, ± 1, ± 2, ± 3, …. В выражении (31) для формулы Бине имеется функция (-1)n, которая принимает значения -1 и +1 в дискретных точках n = 0, ± 1, ± 2, ± 3, …. Рассмотрим теперь тригонометрическую функцию cos(πx), которая принимает значения -1 и +1 в дискретных точках x = 0, ± 1, ± 2, ± 3, …. Это простое наблюдение является основанием для того, чтобы дискретную функцию (31) заменить непрерывной функцией.
Определение 1. Следующая непрерывная функция называется квази-синусоидальной функцией Фибоначчи:
| (32) |
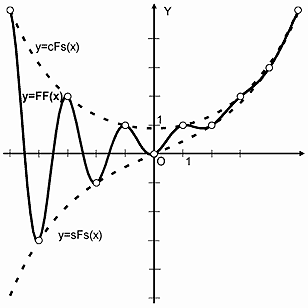
Рисунок 3. График квази-синусоидальной функции Фибоначчи
Существует следующее соотношение, связывающее числа Фибоначчи Fn, задаваемые (31) и квази-синусоидальную функцию Фибоначчи, задаваемую (32):
| (33) |
где n= 0, ±1, ±2, ±3, ….
График квази-синусоидальной функции Фибоначчи представляет собой квази-синусоидальную кривую (Рис.3), которая в дискретных точках x = 0, ± 1, ± 2, ± 3, … совпадает с числами Фибоначчи, задаваемыми (33). При этом графики симметричных гиперболических функций Фибоначчи (Рис. 1) являются огибающими графика квази-синусоидальной функции Фибоначчи (на Рис. 3 графики симметричного гиперболического синуса и косинуса Фибоначчи изображены пунктиром).
Квази-синусоидальная функция Фибоначчи (32) имеет «рекуррентные» свойства, подобные числам Фибоначчи (Табл. 4).
Таблица 4. Некоторые тождества для чисел Фибоначчи и квази-синусоидальной функции Фибоначчи
|
Тождества для чисел Фибоначчи |
Тождества для квази-синусоидальной функции Фибоначчи |
|
Fn+2 = F n+1 + Fn: |
FF(x+2) = FF(x+1) + FF(x) |
|
Fn 2 — F n+1 Fn-1 = (-1)n+1 |
[FF(x)]2 - FF(x+1) FF(x-1) = — cos(πx) |
|
Fn+3 + Fn = 2 Fn+2 |
FF(x+3)+FF(x) = 2FF(x+2) |
|
Fn+3 — Fn = 2Fn+1 |
FF(x+3) - FF(x) = 2FF(x+1) |
|
Fn+6 – Fn = 4Fn+3 |
FF(x+6) + FF(x) = 4FF(x+3) |
|
F2n+1 = Fn+12 + Fn2 |
FF(2x+1)=[FF(n+1)]2 + [FF(x)]2 |
Теперь «формула Кассини» (23) в терминах квази-синусоидальной функции Фибоначчи будет представлена в виде одного «непрерывного тождества:
[FF(x)]2 - FF(x+1)FF(x-1) = — cos(πx)
4.2. Трехмерная спираль Фибоначчи
Известно, что тригонометрические синус и косинус могут быть определены как проекция трансляционного движения точки на поверхности бесконечно вращающегося цилиндра с радиусом, равным 1, и осью симметрии, которая совпадает с осью ОХ. Такая трехмерная спираль проектируется в синусоидальную функцию на плоскости, которая описывается комплексной функцией f(x) = cos(x) + isin(x), где ![]() .
.
Если мы предположим, что квази-синусоидальная функция Фибоначчи (32) является проекцией некоторой трехмерной спирали и проведем те же рассуждения, как для тригонометрического синуса, то мы приходим к так называемой трехмерной спирали Фибоначчи (Рис. 4), которая является «фибоначчиевым» аналогом вращающегося цилиндра, использованного нами для определения функции тригонометрического синуса.
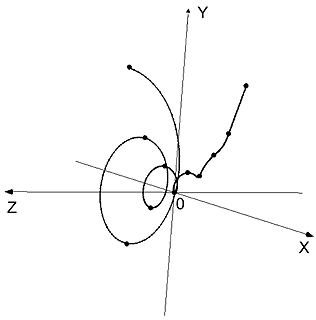
Figure 4. Трехмерная спираль Фибоначчи
Определение 2. Следующая функция называется трехмерной спиралью Фибоначчи:
| СFF(x) = |
(34) |
Эта функция по своей форме напоминает спираль, которая нанесена на поверхность кратера с расширяющимся концом (Рис. 4).
В работе [7] для трехмерной спирали Фибоначчи (34) доказана следующее рекуррентное соотношение:
| СFF(x+2) = СFF(x+1) + СFF(x). | (35) |
Заметим, что рекуррентное соотношение (35) подобно рекуррентному соотношению (4).
4.3 Золотой Шофар
Рассмотрим реальную и мнимую части в выражении (34):
| Re[CFF(x)] = |
(36) |
| Im[CFF(x)] = |
(37) |
Если принять реальную составляющую (36) как функцию y(x) и мнимую составляющую (37) как функцию z(x), можно получить следующую систему уравнений:
| y(x) — |
(38) |
z(x) = ![]() .
.
Возведем в квадрат оба выражения системы уравнений (38) и сложим их. Принимая y и z независимыми переменными, получаем из (38) следующую поверхность второго порядка.
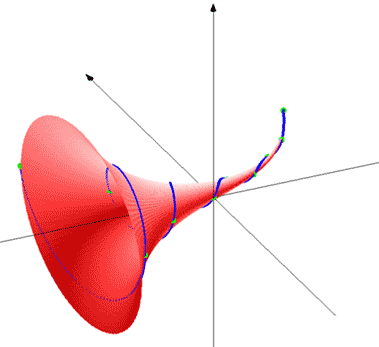
Определение 3. Следующая поверхность второго порядка будем называть поверхностью «Золотой Шофар» (Рис. 5):
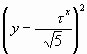 + z2 = + z2 = 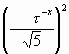 . . |
(39) |
|
| |
Как следует из Рис. 5, Золотой Шофар по своей форме напоминает горн или кратер с расширяющимся раструбом. В переводе с иврита слово «Шофар» означает горн как символ силы и могущества. В Шофар трубят в Судный День (Йом Кипур).
|
| ||||
|
Рисунок 6. Проекция Золотого Шофара на плоскость XOY |
Рисунок 7. Проекция Золотого Шофара на плоскость XOZ |
Формула (39) для поверхности «Золотой Шофар» может быть представлена в терминах симметричных гиперболических функций Фибоначчи (18) и (19):
| z2 = [cFs(x) – y][sFs(x) + y]. | (40) |
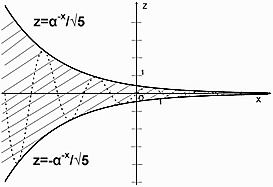
Проекция Золотого Шофара на ось XOY показана на Рис. 6. Золотой Шофар проецируется в пространство между графиками симметричного гиперболического синуса и косинуса (Рис. 1). При этом трехмерная спираль Фибоначчи (34) проецируется в квази-синусоидальную функцию Фибоначчи (32).
Функция (34) лежит на Золотом Шофаре «пронизывает» плоскость XOY в точках, которые соответствуют членам ряда Фибоначчи (Рис. 6).
Проекция Золотого Шофара на плоскость XOZ показана на Рис. 7. Золотой Шофар проецируется в пространство между графиками двух экспоненциальных функций ![]() и
и ![]() .
.
5. Математическая модель «гиперболической Вселенной» с «шофароподобной» топологией
В 2004 г. опубликована сенсационная статья [28] космологического характера. На основе экспериментальных данных, полученных в 2003 с помощью NASA's Wilkinson Microwave Anisotropy Probe (WMAP) в статье [28] выдвинута новая гипотеза о структуре Вселенной. В соответствии с этой гипотезой геометрия Вселенной является гиперболической, а Вселенная по своей форме напоминает горн или трубу с расширяющимся раструбом.
На основе данных полученных немецкими астрофизиками в [28] авторы высказывают следующее предположение:
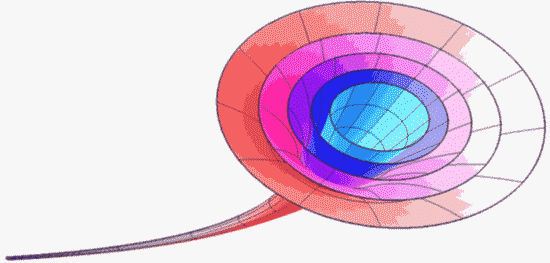
Предположение 1. Вселенная имеет «шофароподобную» топологию (Рис.8).
На Рис. 8 приведено изображение гиперболического пространства с «шофароподбной» топологией.
|
| |
Золотое сечение, и связанные с ним числа Фибоначчи, отображают гармонию Вселенной, как единение частей в целом. С другой стороны в работах [4-7] было показано, что рекуррентные последовательности Фибоначчи порождают новый класс гиперболических функций обладающих не только всеми свойствами классических гиперболических функций, но и рекуррентными свойствами.
Этот синтез гармонии, рекурсии и гиперболических функций, авторы назвали золотым гиперболическом подходом.
Из Предположения 1 вытекает актуальность использования золотого гиперболического подхода [7] для современной физики и космологии.
6. Дальнейшее развитие «золотых» математических моделей
6.1. Обобщенные числа Фибоначчи
В работе [8], как результат исследования «диагональных сумм» треугольника Паскаля, введены так называемые обобщенные числа Фибоначчи. При заданном целом р=0, 1, 2, 3,... обобщенные числа Фибоначчи задаются следующим рекуррентным соотношением:
| Fp(n+1) = Fp(n)+Fp(n-p) для n>p+1; | (41) |
| Fp(1) = Fp(2) =... = Fp(p+1) = 1 | (42) |
Числовые ряды, соответствующие формулам (41), (42), названы в [8] p-числами Фибоначчи.
Доказано [8], что p-числа Фибоначчи могут быть выражены через биномиальные коэффициенты в виде:
| (43) |
Заметим, что выражения (41), (42) задают бесконечное число новых рекуррентных числовых рядов, так как каждому р соответствует свой числовой ряд. В частности, при р=0 рекуррентная формула (41) при начальном условии (42) «генерирует» двоичный ряд чисел: 1, 2, 4, 8, 16, 32,..., а при р=1 – классический ряд Фибоначчи (3). При этом для случая р=1 формула (43) принимает вид формулы
| (44) |
широко известной в комбинаторике.
При р=1 формула (43) принимает вид формулы
| (45) |
которая задает связь чисел Фибоначчи (3) с биномиальными коэффициентами.
6.2. Золотые р-пропорции и «золотые» алгебраические уравнения
Как известно [1-3], отношение соседних чисел Фибоначчи Fn/Fn-1 в пределе стремится к золотой пропорции. В работе [8] доказано, что отношение соседних р-чисел Фибоначчи Fp(n)/Fp(n-1) в пределе стремится к некоторому положительному числу t р, которое является положительным корнем следующего алгебраического уравнения:
| xр+1 = xр + 1. | (46) |
Число t р было названо в [8] золотой р-пропорцией на том основании, что при р=1 число t р совпадает с классической золотой пропорцией. Само уравнение (46) было названо в [9] «золотым» алгебраическим уравнением на том основании, что при р=1 уравнение (46) сводится к уравнению (1).
Заметим, что при р=0 число t р=t 0 =2, а при р=Ґ t р=t Ґ =1. Это означает, что между числовыми константами 2 и 1 на числовой оси находится бесконечное количество числовых констант t р, которые выражают некоторые глубокие математические свойства треугольника Паскаля.
Из уравнения (46) непосредственно вытекает следующее тождество, которое связывает степени золотой р-пропорции:
| (47) |
Уравнение (46) является уравнением (р+1)-й степени и имеет, следовательно, р+1 корней x1, x2, x3, …, xp, xp+1. В дальнейшем будем считать, что корень x1 всегда совпадает с золотой р-пропорцией t p, то есть, x1 = t p. Из уравнения (46) непосредственно вытекает следующее тождество, справедливое для любого из его корней x1, x2, x3, …, xp, xp+1:
| (48) |
где n = 0, ±1, ±2, ±3, …; xk – корень уравнения (46); k = 1, 2,..., р+1.
В работе [9] доказаны следующие свойства корней уравнения (46):
| х1+х2+х3+х 4+... +хр+хр+1 =1 | (49) |
| х1х2х3х 4...хр-1хрх р +1 = (-1)p | (50) |
Кроме того, доказано [9], что для заданных целых р=1, 2, 3,... и k=1, 2, 3, …, p для корней характеристического уравнения (46) выполняется следующее тождество:
| х1k + х2k + х3k + х4+... +хрk + хр+1k = 1. | (51) |
В работе [9] доказано также, что существует бесконечное число алгебраических уравнений, производных от «золотого» уравнения (46), причем все они имеют общий корень – золотую р-пропорцию t p. Общий вид такого уравнения имеет вид:
| (52) |
где Fp(n-р+1) и Fp(n-р-t) – р-числа Фибоначчи, задаваемые (41), (42), nі р+1.
В частности, для случая р=1 общее уравнение (52) принимает следующий вид:
| t n = Fnt + Fn-1, | (53) |
где Fn, Fn-1 – числа Фибоначчи.
При n=4 уравнение (53) принимает следующий вид:
| x4 = 3x + 2. | (54) |
Уравнения (54) приводит нас к неожиданному результату, которое выходит за пределы математики. Оказывается, что уравнение (54) описывает энергетическое состояние молекулы бутадиена – ценного химического вещества, которое используется при производстве каучука. Известный американский физик, Лауреат Нобелевской Премии Ричард Фейнман выразил свое восхищение по поводу уравнения (54) в следующих словах: «Какие чудеса существуют в математике! Согласно моей теории золотая пропорция древних греков дает минимальное энергетическое состояние молекулы бутадиена».
Этот факт сразу же повышает наш интерес к «золотым» алгебраическим уравнениям, задаваемым (52) и (53). Возможно, что именно эти уравнения могут быть использованы в качестве «золотых» математических моделей энергетических состояний молекул других физических веществ.
6.3. Обобщенный принцип Золотого Сечения
Рассмотрим основное тождество для золотой р-пропорции, задаваемое (47). Разделим все члены тождества (47) на ![]() . В результате получим следующее тождество, задающее «Единицу»:
. В результате получим следующее тождество, задающее «Единицу»:
| (55) |
Используя (47), (55), можно сконструировать следующую «динамическую» модель разложения «Единицы» по степеням золотой р-пропорции:
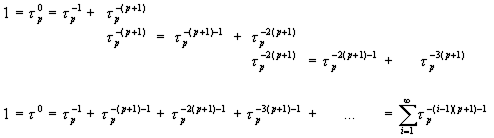 |
(56) |
Основным результатом проведенного исследования, изложенном в [13], является получение весьма общего тождества, позволяющего представить «Единицу» как сумму степеней золотой р-пропорции:
|
|
(57) |
Заметим, что при р=0 тождество (57) принимает следующий вид:
| (58) |
Известно [29], что тождество (58) выражает так называемый «Принцип дихотомии», который пришел к нам из античной науки («Апории Зенона») и который широко используется в математике и других науках.
Наконец, при р=1 тождество (57) принимает вид:
| (59) |
Заметим, что тождество (59) выражает так называемый «Принцип Золотого Сечения» [29], который также пришел к нам из античной науки.
Следовательно, тождество (57) задает нам более общий научный принцип деления целого на части, который назван в [13]«Обобщенным Принципом Золотого Сечения». Ясно, что этот общий принцип содержит в себе в качестве частных случаев «Принцип Дихотомии» (р=0) и «Принцип Золотого Сечения» (р=1).
6.4. Обобщенные формулы Бине и непрерывные функции для р-чисел Фибоначчи и Люка
В работе [10] выведены обобщенные формулы Бине, позволяющие представить аналитически обобщенные числа Фибоначчи. Доказано, что для заданного целого р>0 любое р-число Фибоначчи Fp(n) (n=0, ±1, ±2, ±3, …) может быть выражено через корни «золотого» алгебраического уравнения (46) в следующем виде:
| Fp (n) = k1(x1)n + k2(x2)n + … + kp+1(xр+1) n | (60) |
где x1, x2, …, xp+1 — корни «золотого» алгебраического уравнения (46), а k1, k2, …, kp+1 – постоянные коэффициенты, которые являются решением системы уравнений:
|
Fp (0) = k1 + k2 + … + kp+1=0 Fp (1) = k1x1 + k2x2 +...+ kp+1xр+1=1 Fp (2) = k1(x1)2 + k2(x2)2 + … + kp+1(xр+1) 2=1 ...................................................................... Fp (р) = k1(x1)р + k2(x2)р + … + kp+1(xр+1) р=1 |
(61) |
В частности, при р=1 р-числа Фибоначчи сводятся к классическим числам Фибоначчи Fn и для этого случая выражение (60) сводятся к хорошо известному в «теории чисел Фибоначчи» [2, 3] выражению:
| Fn = k1(x1)n + k2(x2)n, | (62) |
где x1, x2 – корни алгебраического уравнения (1), задаваемые выражениями:
| x1 = |
(63) |
а коэффициенты k1, k2 являются решениями системы уравнений:
| F0 = k1 + k2 = 0 F1) = k1τ + k2(-1/τ) = 1 |
(64) |
После решения системы уравнений (64) мы получаем следующие выражения для коэффициентов k1 и k2:
| k1 = |
(65) |
Подставляя выражения (63), (64) в формулу (62), получим хорошо известную формулу Бине для чисел Фибоначчи:
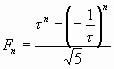 . . |
(66) |
Как известно [2, 3], числа Люка Ln могут быть выражены через корни x1, x2 в следующем виде:
| (67) |
В работе [10] доказано, что сумма n-х степеней корней x1, x2, …, xp+1 «золотого» алгебраического уравнения (46) задает новый класс рекуррентных числовых последовательностей, названных в [10] р-числами Люка Lp(n), где р=0, 1, 2, 3,..., то есть,
| Lp (n) = (x1)n + (x2)n + … + (xр+1)n | (68) |
С использованием свойств корней алгебраического уравнения (46), задаваемых (48)-(51) доказано, что числовая последовательность, задаваемая (68), может быть также вычислена по рекуррентной формуле:
| Lp (n) = Lp (n-1) + Lp (n-р-1) | (69) |
при следующих начальных условиях:
| Lp (0) = р+1 | (70) |
| Lp (1) = Lp (2) =... = Lp (р) = 1. | (71) |
Табл. 5 задает значения р-чисел Люка для начальных значений р=1, 2, 3, 4.
Таблица 5. Р-числа Люка
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
L1(n) |
2 |
1 |
3 |
4 |
7 |
11 |
18 |
29 |
47 |
76 |
123 |
199 |
322 |
|
L2(n) |
3 |
1 |
1 |
4 |
5 |
6 |
10 |
15 |
21 |
31 |
46 |
67 |
98 |
|
L3(n) |
4 |
1 |
1 |
1 |
5 |
6 |
7 |
8 |
13 |
19 |
26 |
34 |
47 |
|
L4(n) |
5 |
1 |
1 |
1 |
1 |
6 |
7 |
8 |
9 |
10 |
16 |
23 |
31 |
Таким образом, основным результатом работы [10] является обобщение формул Бине и открытие нового класса рекуррентных числовых последовательностей, обобщенных чисел Люка, задаваемых (68)-(71), которые, вполне вероятно, могут быть использованы в качестве моделей явлений окружающего нас мира.
Как было показано выше, гиперболические функции Фибоначчи и Люка (13)-(16) и (18)-(21) являются обобщением формул Бине (9)-(10) на непрерывную область. Поскольку в работе [10] приведены обобщенные формулы Бине (60), (68), позволяющие выразить р-числа Фибоначчи и р-числа Люка через корни «золотого» алгебраического уравнения (46), естественной является постановка вопроса о выведении непрерывных формул для р-числа Фибоначчи и р-числа Люка, подобным формулам для гиперболических функций Фибоначчи и Люка. Такая попытка сделана в работе [11]. Как оказалось, выведенные формулы являются значительно более сложными, чем формулы (13)-(16) и (18)-(21), но тем не менее, результаты работы [11] также можно трактовать как один из вариантов «золотых» математических моделей, которые, возможно, когда-либо могут быть востребованы теоретическим естествознанием.
6.5. Матрицы Фибоначчи
В последние десятилетия «Теория чисел Фибоначчи» дополнилась новыми математическими результатами. Одним из них является теория матрицы специального типа, названной Q-матрицей [2]. Последняя представляет собой простейшую квадратную матрицу размером 2ґ 2 следующего вида:
| (72) |
Заметим, что детерминант Q-матрицы равен -1, то есть,
| Det Q = -1. | (73) |
Но какое отношение имеет Q-матрица к числам Фибоначчи? Чтобы отвечать на этот вопрос, необходимо возвести Q-матрицу в n-ю степень. Тогда мы получим:
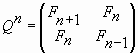 |
(74) |
где Fn-1, Fn, Fn+1 числа Фибоначчи.
Используя (73), легко доказать, что детерминант матрицы (74) задается выражением:
| Det Qn = (-1)n, | (75) |
где n – целое число.
С другой стороны, детерминант матрицы (74) равен:
| Det Qn = Fn-1Fn+1 — |
(76) |
Напомним, что тождество (76), задающее связь трех соседних чисел Фибоначчи, было выведено еще в 17-м веке знаменитым астрономом Кассини; поэтому формула (76) называется также «формулой Кассини» [26]. Отсюда вытекает, что Q-матрица выражает одно из наиболее важных свойств чисел Фибоначчи, задаваемое (76), а свойство Q-матрицы, задаваемое (75), можно рассматривать как компактную запись «формулы Кассини»!
Можно использовать идею «фибоначчиевой» Q-матрицы (72) для получения обобщенных матриц Фибоначчи. В работе [12] ведена в рассмотрение квадратная матрица специального типа, которую названа Qp-матрицей:
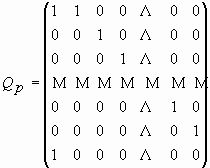 |
(77) |
где индекс p принимает следующие значения: 0, 1, 2, 3, ….
Заметим, что Qp-матрица представляет собой квадратную (p+1)ґ (p+1)-матрицу. Она содержит единичную pґ p матрицу, ограниченную последней строкой, состоящей из нулей, и первым столбцом, который состоит из нулей, ограниченных единицами. Для случаев p = 0, 1, 2, 3, 4 Qp-матрицы имеют следующий вид соответственно:
Q0 = (1); ![]() ;
; 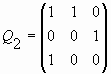 ;
;
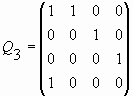 ;
; 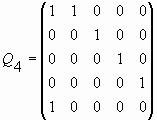 .
.
Основным результатом работы [12] является доказательство следующего выражения для Qp-матрицы, возведенной в степень n:
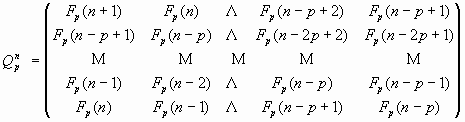 |
(78) |
где р =0, 1, 2, 3, …, n = 0, ± 1, ± 2, ± 3, …, а элементами матрицы являются р-числа Фибоначчи, задаваемые рекуррентным соотношением (41) при начальных условиях (42).
В работе [12] доказано также, что детерминант матрицы (78) задается следующим выражением:
| Det |
(79) |
где p = 0, 1, 2, 3, …; n = 0, ± 1, ± 2, ± 3, ….
Таким образом, в работе [12] разработана теория квадратных матриц, обладающих уникальным свойством: согласно (79) детерминант любой такой матрицы всегда равен по абсолютной величине 1, а знак единицы зависит от произведения двух целых чисел pґ n (р =0, 1, 2, 3, …, n = 0, ± 1, ± 2, ± 3). Если это произведение является четным, то детерминант матрицы (78) равен +1, в противном случае детерминант равен -1.
Ясно, что матрицы (77), (78) могут быть использованы для расширения «фибоначчиевых» исследований. При этом выражение (79) можно рассматривать как обобщение «формулы Кассини» (76). Например, для случая р=2 обобщенная «формула Кассини» выглядит следующим образом:
|
(80) |
Подобно «формуле Кассини» (78), задающей связь между тремя соседними числами Фибоначчи, формула (80) связывает пять соседних 2-числа Фибоначчи F2(n-3), F2(n-2), F2(n-1), F2(n) и F2(n+1) для любого заданного числа n (n = 0, ± 1, ± 2, ± 3, …).
Подчеркнем еще раз, что обобщенных «формул Кассини», подобных (80) и основанных на (79), теоретически бесконечно, причем их столько же, сколько существует натуральных чисел, поскольку р=1, 2, 3,....
6.6. «Золотые» матрицы
В работе [13] введены так называемые «золотые» матрицы. Представим матрицу (74) в виде двух матриц, задаваемых для четных (n=2k) и нечетных (n=2k+1) значений степени n:
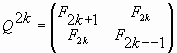 |
(81) |
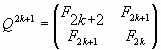 |
(82) |
Используя соотношение (22), мы можем записать матрицы (81), (82) в терминах симметричных гиперболических функций Фибоначчи (18), (19):
| (83) |
| (84) |
где k – дискретная переменная, k=0, ± 1, ± 2, ± 3, ….
Если теперь заменить дискретную переменную k в матрицах (83), (84) непрерывной переменной x, то мы придем к двум необычным матрицам, которые являются функциями от переменной x:
| (85) |
| (86) |
Ясно, что матрицы (85), (86) являются обобщением Q-матрицы (74) на непрерывную область. Они имеют ряд необычных математических свойств. Например, для ![]() матрица (85) принимает следующую форму:
матрица (85) принимает следующую форму:
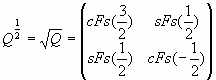 |
(87) |
Невозможно вообразить, что означает «корень квадратный из Q-матрицы», но именно такая «фибоначчивая фантазия» вытекает из выражения (87)!
Для вычисления детерминантов матриц (85), (86) мы можем воспользоваться свойствами симметричных гиперболических функций Фибоначчи, задаваемыми (24), (25).
Если вычислить детерминанты матриц (85), (86), то с учетом (24) и (25), мы придем к весьма необычному математическому тождеству для матриц (85), (86), которое справедливо для любого значения непрерывной переменной x:
| Det Q2x = 1 | (88) |
| Det Q2x+1 = - 1 | (89) |
Вновь обращаясь к «формуле Кассини», задаваемой (75) и (76), мы приходим к неожиданному заключению, что необычные тождества (88), (89) являются ни чем иным, как обобщением «формулы Кассини» (75) на непрерывную область!
В настоящее время трудно предсказать, в какой области теоретического естествознания могут быть использованы матрицы (78), (85), (86), обладающие необычными математическими свойствами (79), (88), (89). Однако уже сейчас найдено их весьма эффективное применение в теории кодирования и криптографии [13, 24, 25].
7. Заключение
Таким образом, в работах авторов [4-25] по существу создан новый математический аппарат для моделирования «гиперболических миров» Природы. Наиболее важными «золотыми» математическими моделями являются следующие:
1. Гиперболические функции Фибоначчи и Люка. Первым важным следствием их введение является осознание того, что классические гиперболические функции (12), (13), которые использовались в математике и теоретической физике не являются единственной математической моделью «гиперболических миров». Параллельно с гиперболической геометрией, основанной на классических гиперболических функциях («гиперболическая геометрия Лобачевского», «четырехмерный мир Минковского» и др.), в Природе наблюдается и другая гиперболическая геометрия, основанная на гиперболических функциях Фибоначчи и Люка. «Золотой» гиперболический мир, основанный на такой геометрии («геометрии Боднара»), существует объективно и независимо от нашего сознания. Этот мир с удивительной настойчивостью проявляет себя, прежде всего, в живой природе, в частности, он обнаруживают себя на поверхности сосновых шишек, ананасов, кактусов, головок подсолнечника, корзинок цветов и т.д. в виде филлотаксисных спиралей, основанных на числах Фибоначчи, числах Люка и других числовых рекуррентных рядах подобного типа («Закон филлотаксиса»). Заметим, что гиперболические функции Фибоначчи и Люка [4-7], лежащие в основе явления филлотаксиса, не являются «выдумкой» математиков-фибоначчистов, а отражают важнейшую математическую закономерность, лежащую в основе геометрии живой природы.
2. Золотой Шофар. Кроме гиперболических функций Фибоначчи и Люка, которые могут быть использованы для моделирования явления филлотаксиса, поверхность «Золотой Шофар» также может быть использована для моделирования «гиперболических миров». Статья «Hyperbolic Universes with a Horned Topology and the CMB Anisotropy» [28] оказалась огромным сюрпризом для авторов, поскольку она показала, что геометрия Вселенной по своей структуре является «шофароподобной».
3. Что касается «золотых» математических моделей, основанных на р-числах Фибоначчи, золотых р-пропорциях, «золотых» алгебраических уравнениях и вытекающих из них обобщенных формул Бине для р-чисел Фибоначчи и р-чисел Люка, а также матриц Фибоначчи, основанных на р-числах Фибоначчи, и «золотых» матрицах», основанных на гиперболических функциях Фибоначчи, то можно с уверенностью предположить, что данные модели также могут получить применение для моделирования процессов, протекающих в Природе. Очень важно при этом подчеркнуть, что все эти модели естественным образом вытекают из треугольника Паскаля, который широко используется в структурах Природы.
В заключение авторы хотели бы обратить внимание на следующее странное обстоятельство. Можно только удивляться тому факту, что в течение многих столетий математики и физики-теоретики не уделяли должного внимания развитию математического аппарата для моделирования «золотого» гиперболического мира, который существует в реальной действительности. Возможно, причиной этого является тот факт, что «золотой» гиперболический мир имеет большее отношение к биологии и ботанике, чем к физике. Однако, к чести определенной группы физиков-теоретиков, в конце 20-го столетия отношение к Золотому Сечению и числам Фибоначчи, лежащие в основе «золотого» гиперболического мира, в современной теоретической физике начинает быстро изменяться. Работы [30-38] являются свидетельством повышенного интереса к Золотому Сечению и числам Фибоначчи со стороны физиков-теоретиков. Работы Бутусова, Шехтмана (Shechtman), Маулдина (Mauldin), Вильяма (William), Ель Нашие (El Naschie), Владимирова и других показывают, что невозможно вообразить дальнейшее развитие физических и космологических исследований без «Золотого Сечения». В этом отношении блестящим примером является статья проф. Ель Нашие [36], в которой достаточно убедительно показано, что большинство фундаментальных математических констант может быть выражено через золотую пропорцию. В этой связи вряд ли можно считать случайностью тот факт, что известный российский физик-теоретик проф. Владимиров (Московский университет) заканчивает свою книгу «Метафизика» [38] следующими словами: «Таким образом, можно утверждать, что в теории слабых взаимодействий возникает соотношение Золотого Сечения, которое играет важную роль в различных сферах Науки и Искусства».
Литература
1. Воробьев Н.Н. Числа Фибоначчи. – М.: Наука, 1978. – 144 с.
2. Hoggat V.E. Fibonacci and Lucas Numbers. - Palo Alto, California: Houghton-Mifflin, 1969. – 92 с.
3. Vajda S. Fibonacci & Lucas Numbers, and the Golden Section Theory and Applications. — Ellis Horwood limited, 1989. — 190 с.
4. Стахов А.П., Ткаченко И.С. Гиперболическая тригонометрия Фибоначчи // Докл. НАН Украины. – 1993, вып. 7. — С. 9-14.
5. Stakhov A.P. Hyperbolic Fibonacci and Lucas Functions: A New Mathematics for the Living Nature. — Vinnitsa: ITI, 2003. ISBN 966-8432-07-X. – 240 с.
6. Stakhov A., Rozin B. On a new class of hyperbolic function // Chaos, Solitons & Fractals. – 2004, 23(2). P. 379-389.
7. Stakhov A., Rozin B. The Golden Shofar // Chaos, Solitons & Fractals. - 2005, 26(3). P. 677-684.
8. Стахов А.П. Введение в алгоритмическую теорию измерения. – М.: Советское радио, 1977. — 288 c.
9. Stakhov A., Rozin B. The «golden» algebraic equations // Chaos, Solitons & Fractals. — 2005, 27 (5). – P. 1415-1421.
10. Stakhov A., Rozin B. Theory of Binet formulas for Fibonacci and Lucas p-numbers // Chaos, Solitons & Fractals, 2005, 27 (5). – P. 1162-1177.
11. Stakhov A., Rozin B. The continuous functions for the Fibonacci and Lucas p-numbers. — Chaos, Solitons & Fractals, 2006, 28 (4). – P. 1014-1025.
12. Stakhov A.P. A generalization of the Fibonacci Q-matrix // Докл. НАН Украины, 1999, No 9. — С. 46-49.
13. Stakhov A. The Generalized Principle of the Golden Section and its Applications in Mathematics, Science and Engineering // Chaos, Solitons & Fractals, 2005, 26 (2). — P. 263-289.
14. Стахов А.П. Алгоритмическая теория измерения. – М.: Знание, 1979. — 64 c.
15. Stakhov A.P. The Golden Section in the measurement theory // An International Journal «Computers & Mathematics with Applications», 1989, Vol.17, No 4-6. – P. 613-638.
16. Стахов A.П. Обобщенные Золотые Сечения и новый подход к геометрическому определению числа // Украинский математический журнал, 2004, том 56, № 8. — С. 1143-1150.
17. Stakhov A.P. The Golden Section and Modern Harmony Mathematics // Applications of Fibonacci Numbers, 1998, Vol. 7. – P. 393-399.
18. Стахов А.П. Сакральная геометрия и математика гармонии // М.: «Академия Тринитаризма», Эл № 77-6567, публ.11176, 26.04.2004.
19. Стахов А.П. Математика Гармонии как новое междисциплинарное направление современной науки // М.: «Академия Тринитаризма», Эл № 77-6567, публ.12371, 19.08.2005
20. Stakhov A. Fundamentals of a new kind of Mathematics based on the Golden Section // Chaos, Solitons & Fractals, 2005, 27 (5). – P. 1124-1146.
21. Стахов A.П. Коды золотой пропорции. – М.: Радио и связь, 1984. — 152 c.
22. Stakhov A.P. Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic // The Computer Journal, 2002, Vol. 45, No. 2. — P. 222-236.
23. Стахов А.П. Троичный принцип Брусенцова, система счисления Бергмана и «золотая» троичная зеркально-симметричная арифметика // М.: «Академия Тринитаризма», Эл № 77-6567, публ.12355, 15.08.2005
24. Stakhov A., Massingue V., Sluchenkova A.A. Introduction into Fibonacci coding and cryptography. – Kharkov: Publisher «Osnova», 1999. – ISBN 5-7768-0638-0. – 236 p.
25. Стахов А.П. Кодирование данных, основанное на фибоначчиевых матрицах // Труды Международной конференции «Проблемы гармонии, симметрии и Золотого Сечения в природе, науке и искусстве». Винница: Изд-во Винницкого государственного аграрного университета, 2003. — C. 311-325.
26. Стахов А.П. Формула Кассини // М.: «Академия Тринитаризма», Эл № 77-6567, публ.12542, 01.11.2005.
27. Боднар О.Я. Золотое Сечение и неевклидова геометрия в природе и искусстве. – Львов: Свит, 1994. – 204 с.
28. Aurich R., Lusting S., Steiner F., Then H. Hyperbolic Universes with a Horned Topology and the CMB Anisotropy // Classical Quantum Gravity, 2004, No. 21. – P. 4901-4926.
29. Шевелев И.Ш. Метаязык живой природы. – Кострома: Воскресенье 2000. — 352 c.
30. Гратиа Д. Квазикристаллы // Успехи физических наук, 1988, том. 156. — C. 347-363.
31. Бутусов К.П. Золотое Сечение в солнечной системе // Сборник «Проблемы исследования Вселенной», 1978, №7. – С. 475-500.
32. Mauldin R.D. and Willams S.C. Random recursive construction // Trans. Am. Math. Soc., 1986, 295. – C. 325-346.
33. El Naschie M.S. On dimensions of Cantor set related systems // Chaos, Solitons & Fractals, 1993, 3. – P. 675-685
34. El Nashie M.S. Quantum mechanics and the possibility of a Cantorian space-time // Chaos, Solitons & Fractals, 1992, 1. – P. 485-487
35. El Nashie M.S. Is Quantum Space a Random Cantor Set with a Golden Mean Dimension at the Core? // Chaos, Solitons & Fractals, 1994, 4(2). – P. 177-179
36. El Naschie M.S. Elementary number theory in superstrings, loop quantum mechanics, twistors and E-infinity high energy physics // Chaos, Solitons & Fractals, 2006 27(2). – P. 297-330.
37. Владимиров Ю.С.. Кварковый икосаэдр, заряды и угол Вайнберга // Труды Международной конференции «Проблемы гармонии, симметрии и Золотого Сечения в природе, науке и искусстве». Винница: Изд-во Винницкого государственного аграрного университета, 2003. — C. 69-79.
38. Владимиров Ю.С. Метафизика. – M.: Бином, 2002. – 550 с.
Стахов А.П., Розин Б.Н. «Золотые» гиперболические модели Природы // «Академия Тринитаризма», М.,
|
|