|
|
|
Батанов М.
1. Представления об l mё n -вакууме
В современном Естествознании физический вакуум – это не тривиальная пустая арена, на фоне которой проистекает жизнь материальных объектов, а самостоятельный, чрезвычайно сложный объект исследований. Наиболее интригующим следствием данных воззрений является вывод о том, что физический вакуум представляет собой многоплановую, иерархическую структуру, превосходящую по сложности самого субъекта исследований – Человека.
Существует множество подходов к изучению вакуума: от динамических теорий механического эфира, до различных вариантов многомерных теорий струн. В данной статье предлагается еще один подход к изучению вакуума на базе двух основополагающих принципов: «принцип постоянства скорости света в вакууме» и «принцип усредненной отсутственности». Поясним суть этих принципов.
1). «Принцип постоянства скорости света в вакууме» гласит: что скорость распространения волновых возмущений в вакууме равна скорости света и ничего не зависит кроме как от свойств самого вакуума. Данный эйнштейновский принцип связан с представлениями о вакууме, как о некой «упругой» среде, в которой распространяются различные возмущения. Предельная скорость вакуумных возмущений равна скорости света
с = 299792458 м/с.
Любое волновое возмущение, распространяющееся в вакууме с данной скоростью света, называется светом (или электромагнитной волной). В вакууме распространяются световые волны в огромном частотном диапазоне, но все они имеют одну и туже скорость с. Лучи (эйконалы) света определенного частотного диапазона обладают свойством повторять метрико-динамическую структуру вакуума, т. е. распространяются по геодезической линии, лежащей на 4-мерном ландшафте вакуума. При этом не зависимо от масштаба и сложности 4-ландшафта вакуума скорость распространения лучей света с остается неизменной.
2). «Принцип усредненной отсутственности» или просто «принцип отсутственности» гласит: — если, что-либо рождается из Великой Пустоты, то обязательно в виде пары с взаимно – компенсирующими (противоположными) свойствами. Принцип отсутственности требует, что если что-либо (волны или частицы, …) рождаются из усредненной ПУСТОТЫ то обязательно в виде двух взаимно противоположных сущностей, которые в среднем полностью компенсируют проявления друг друга. В отношении физического вакуума это означает, что если из него рождается частица, то обязательно в паре с ее антикопией (т. е. античастицей), волна – в паре с антиволной, луч света – в паре с антилучем (т. е. с противоположно направленным лучом света с противоположным спином (поляризацией) и т. д.
Все дальнейшие свето-геометрические построения в настоящей работе основаны на этих двух основополагающих принципах и на отказе от какой-либо примитивной субстанциональной материальности, лежащей в основе природы вакуума. В рамках развиваемых здесь представлений вакуум – это многослойная протяженность реальности, каждый продольный слой которой «высвечивается» лучами света соответствующего диапазона длин волн. Для того, чтобы «высветить» какой либо слой вакуума нужно посылать лучи света определенного диапазона длин волн l mё n =10m…10nсм, например с помощью радиолокационной установки (см. рис. 1), в различных направлениях. При этом, наблюдая за характером и направлением распространения пробных лучей света можно построить из них свето-геометрическую координатную сетку, размер ячеек которой соизмерим со средней длиной волны <l mё n >пробных сигналов (лучей).
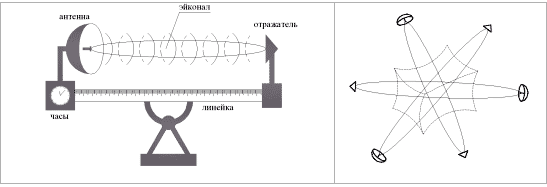
Рис. 1
Зондируя таким образом протяженность окружающей реальности, можно визуализировать (высветить) 4-мерный «светозарный» ландшафт пустоты с характерным масштабом рассмотрения соизмеримым со средней длиной волны <l mё n >пробных (координатных) лучей света. Такой светогеометрический 4-ландшафт будет называть l mё n -вакуумом (т. е. «светозарным» слоем Великой Пустоты, который высвечивается пробными лучами света из диапазона длин волн l mё n =10m…10nсм).
 |
| Рис. 2. координатная сеть на ландшафте недеформированного участка lmё n -вакуума. |
Из определения l mё n -вакуума видно, что сколько диапазонов длин волн можно выделить из всего спектра световых волн столько и l mё n-вакуумов (т. е. свето-геометрических 4-ландшафтов различных масштабов рассмотрения). Таким образом, свето-геометрический (радиолокационный) подход к изучению метрико-динамических свойств протяженной Бездонны (Вакуума) заведомо содержит возможность разложения этой многоуровневой Иерархии на продольные слои с различными масштабами «рассмотрения». При этом, подобно матрешке, мелкомасштабные свето-геометрические 4-ландшафты (l mё n -вакуумы) оказываются вложенными в более крупномасштабные продольные слои той же Светозарной Реальности. Мир устроен так, что на различных участках Светозарного Вакуума различные слои (т. е. l mё n -вакуумы) ведут себя по-разному, но общие свойства l mё n -вакуумов оказываются одинаковыми. Поэтому детальное изучение одного из l mё n-вакуумов дает сразу представление о всех продольных слоях (l mё n-вакуумах) изучаемой Бездонной Иерархии.
Рассмотрим один l mё n -вакуумов более подробно. Для этого на одном из его недеформированных участков пустим пробные лучи света соответствующего диапазона l mё n =10m…10nсм так, чтобы они образовали декартову сетку (см. рис. 2) с характерный размером ребра кубической ячейки
| e ~ 102 <l mё n>. | (1) |
То есть расстояние между двумя пробными лучами света, образующими идеальную декартову координатную сетку на недеформированном участке изучаемого l mё n -вакуума, должно быть примерно на два порядка больше их средней длины волны.
Ниже предлагаются основы универсальной светогеометрии, описывающей метрико-динамические свойства любого l mё n -вакуума из всей светозарной толщи окружающей нас протяженной Реальности.
2. Светогеометрия одного из l mё n -вакуумов
Рассмотрим в начале идеальный недеформированный участок l mё n -вакуума.
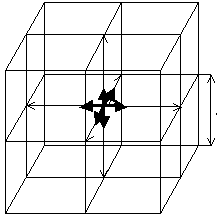
Пусть пробные лучи света со средней длиной волны <l mё n> из произвольно выбранного диапазона l mё n =10m…10nсм образуют в некоторой области одного из слоев Светозарного Вакуума декартову координатную сетку, ячейками которой являются неискаженные кубы с длиной ребра e ~ 102 <l mё n> (см. рис.2).
Выделим из всего рассматриваемого участка l mё n -вакуума объем состоящий из 8 кубиков, имеющих одну общую вершину в точке О (см. рис.2). Будем называть такой объем – согласованным объемом l mё n -вакуума, т. к. предполагается, что метрико-динамические свойства данного согласованного объема соответствуют свойствам каждого подобного объема и всей исследуемой области l mё n -вакуума в целом.
С центральной точкой О, исследуемого согласованного объема, совместим начала 3-векторных базисов, задающих направления ребер всех восьми кубиков.
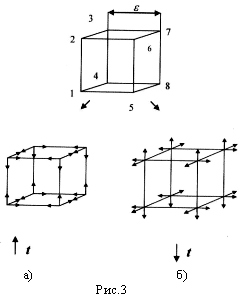
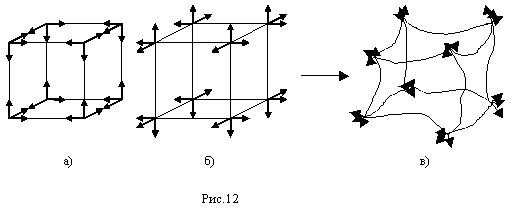
Чтобы понять сколько 3-векторных базисов (или просто 3-базисов) исходит из центральной точки О, искусственно«растащим» эту точку по 8 углам гипотетического кубика (рис.3). При этом сразу становится понятным, что из точки О исходит 8 + 8 = 16 3-базисов (рис.3а,б).
На самом деле 3-векторных базисов на рис. 3а,б лишь восемь. Дело в том, что один из 3-базисов, показанных на рис. 3а, совпадает с диагонально противоположно расположенным 3-базисом, показанным на рис. 3б. Следовательно, исследуемый объем описывается лишь восьмью 3-базисами. Так бы и было, если бы не еще одна степень свободы – вращение 3-базисов.
Будем полагать, что в силу принципа отсутственности, 3-базисы показанные на рис. 3а вращаются «по часовой стрелке», а 3-базисы показанные на рис. 3б вращаются – в противоположную сторону, т. е. «против часовой стрелки». При этом для идеального (т. е. недеформированного) участка l mё n -вакуума, все попарно противоположно вращающиеся 3-базисы в среднем полностью компенсируют проявления вращения друг относительно друга.
- 2.1.1. Векторный (электродинамический или поляризационный)
анализ согласованного объема l mё n -вакуума
Физический смысл вращения 3-базисов, показанных на рис. 3а,б очень прост и связан с поляризацией пробных лучей света.
Напомним, что поляризацией электромагнитной волны (или луча света) называется закон изменения направления вектора электрического поля Е, в плоскости перпендикулярной направлению распространения волны (или луча), вектор магнитного поля изменяется точно по такому же закону.
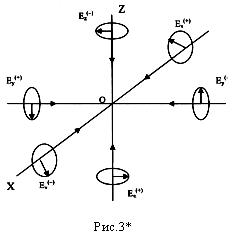
Согласно всеобщего принципа отсутственности по каждой оси в точку О приходит не один, а два взаимно противоположных луча света с взаимно противоположными спинами (т. е. круговыми поляризациями).
Рассмотрим в начале распространение двух встречных лучей света, распространяющихся друг на встречу друга вдоль оси Х (рис.3*). Поляризация этих лучей задается векторами электрического поля Ex(+) и Ex(–), которые в виде комплексных векторов задаются выражениями
| (1a) |
| (1б) |
где
(+) – проекция вектора Ex(+) на ось Z, волны распространяющейся в аффинном пространстве;
Средняя световая волна (луч) распространяющейся в аффинном пространстве вдоль оси Х определяется усредненным выражением
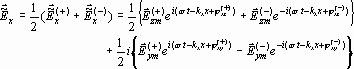 |
(1в) |
В случае согласованности прямой и встречной волн амплитуды и фазы их колебаний равны
Ezm(+) = Ezm(–) = Ezm, Eym(+)= Eym(–) = Eym;
j хz(–)=j хz(+) = j хz, j хy(–)=j хy(+) = j хy.
При этом из (1в) имеем
| (1г) |
С учетом формул Эйлера
![]()
для начала координат (т. е. при х = 0) из (1 г) окончательно получим
| (1д) |
где Ezm – вектор, направленный в вдоль оси Z;
Eym – вектор, направленный в вдоль оси Y.
Принцип отсутственности приводит к выводам, совпадающим с представлениями классической электродинамики. Алсигна лишь препарирует исследуемый процесс и показывает, что при определенных условиях встречные световые волны полностью компенсируют проявления друг друга, а при других условиях их суперпозиция приводит к проявлению усредненной бегущей волны с усредненной эллиптической поляризацией. Это сразу обнаруживается при переходе от векторного представления (1д) к эквивалентной функциональной записи [1]:
| (1е) |
или
| (1ж) |
где 2d = j хz – j хy – разность фаз колебаний ортогональных составляющих;
j 0 = j хz – начальная фаза z-компоненты электрического вектора Ex.
Исключая из выражения (1ж) время, можно найти уравнение траектории конца (годографа) электрического вектора Ex в плоскости ZOY [1]:
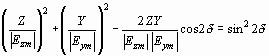 , , |
(1з) |
где введены обозначения
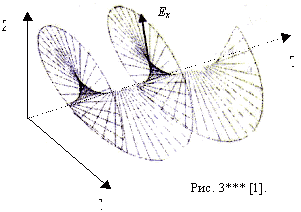
Уравнение (1з) описывает кривую второго порядка и в силу ограниченности модулей ортогональных векторов Ezm и Eym соответствует уравнению эллипса (рис. 3**). Такая световая волна (луч) является эллиптически поляризованной электромагнитной волной. Поведение эллиптически поляризованной волны в точке О во времени показано на рис. 3***.
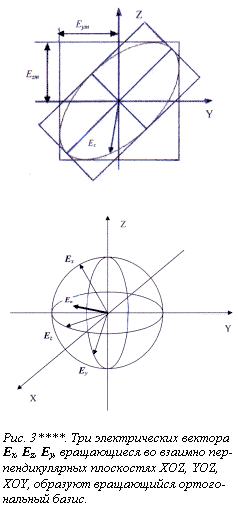
Мы рассмотрели поведение монохроматической бегущей электромагнитной волны (луча света) с усредненным электрическим вектором Ex, распространяющейся вдоль оси X). Аналогичный анализ волн (лучей) с усредненными электрическими векторами Ez и Ey, распространяющимся соответственно вдоль осей Z и Y (рис. 3*) приводит к подобным результатам.
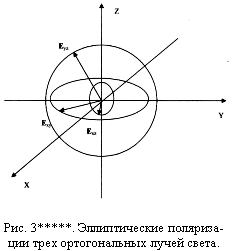 То есть в наиболее общем случае годограф вектора Ez – является наклоненным эллипсом в плоскости XOY, а годограф вектора Eу – является наклоненным эллипсом в плоскости XOZ (рис. 3****). В общем случае модули векторов Ex, Ez и Ey не равны друг другу, потому их годографами могут быть эллипсы различной величины, что и показано на рис. 3*****. Если модули этих векторов равны и их годографами являются круги, то эти три вектора Ex, Ez, Ey образуют причудливо вращающийся, ортогональный базис (рис. 3****).
То есть в наиболее общем случае годограф вектора Ez – является наклоненным эллипсом в плоскости XOY, а годограф вектора Eу – является наклоненным эллипсом в плоскости XOZ (рис. 3****). В общем случае модули векторов Ex, Ez и Ey не равны друг другу, потому их годографами могут быть эллипсы различной величины, что и показано на рис. 3*****. Если модули этих векторов равны и их годографами являются круги, то эти три вектора Ex, Ez, Ey образуют причудливо вращающийся, ортогональный базис (рис. 3****).
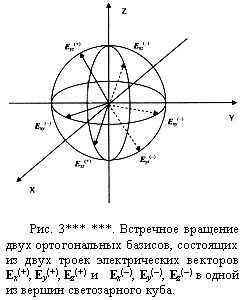
Отличие представлений Алсигны от классических представлений [1], связано с тем, что согласно (1а) и (1б) в каждой 3-мерной «плоскости» XYТ, XZТ и ZYT (рис. 3****), рассматриваемой системы отсчета (начало которой приходится на точку О), вращается не по одному электрическому вектору Ex, Ez и Ey, а по два: Ex(+) и Ex(–), Eу(+) и Eу(–), Ez(+) и Ez(–) (рис. 3*** ***).
 Поскольку, например, выражения (1а) и (1б) могут быть, так же как и (1в), представлены в виде комплексных векторов:
Поскольку, например, выражения (1а) и (1б) могут быть, так же как и (1в), представлены в виде комплексных векторов:
| (1и) |
| (1к) |
Причем согласно исходному принципу отсутственности, вращения электрических векторов Ei(+) и Ei(–), принадлежащих одной плоскости, должно происходить во взаимно противоположные стороны. Что собственно и следует из выражений (1 и) и (1к) где в первом случае в показателе экспоненты вынесенной за скобки имеет место стигнатура {+ –}, а во втором случае – стигнатура { – +}. При этом если, например, электрический вектор Ex(+) вращается в 3-мерной «плоскости» ZYT, то электрический вектор Ex(–) вращается в противоположную сторону, т. е. в 3-мерной «плоскости» ZY(-T), где стрела времени обращена вспять.
Вместе с тем представления Алсигны полностью согласоваться с классическими представлениями, поскольку мы исходим из того, что наблюдаемые величины (в частности ![]() ) должны состоять из ненаблюдаемых (в частности
) должны состоять из ненаблюдаемых (в частности ![]() и
и ![]() ), таким образом, что наблюдаемая величина являться средним арифметическим от двух ненаблюдаемых
), таким образом, что наблюдаемая величина являться средним арифметическим от двух ненаблюдаемых
| (1л) |
- 2.1.2. Решимо
Рассмотрим идеальный случай. Под решимо подразумевается идеальное (совершенно недеформированное и неискаженное), исходное состояние исследуемого участка l mё n -вакуума (см. рис.2). Это состояние в среднем ни как не проявляет себя (кроме как участок совершенно пустой 3-мерной протяженности), но вместе с тем оно переполнено сиянием внутреннего света, т. е. решимо – идеальная 3-мерная пустота, живущая собственной внутренней жизнью. Но внутренняя «жизнь» решимо скрыта от нас абсолютной компенсацией различных взаимно противоположных проявлений различных метрических и динамических аспектов существования исследуемой области l mё n -вакуума.
Встречные световые волны (рис. 3*) с одинаковой амплитудой колебаний могут полностью нейтрализовать проявления друг друга. Например, для встречных волн, распространяющихся вдоль оси Х в точке х = 0, при равных амплитудах их составляющих Ezm(+) = Ezm(–) и Eym(+) = Eym(–) из выражения (1в) имеем
|
(1м) |
Легко проверить, что при j хz(–)=p – j хz(+)выражение в первой фигурной скобке (1м) обращается в ноль
а при j хy(–)=2p – j хy(+)обращается в ноль выражение и во второй фигурной скобке (1м)
В этом случае все выражение (1м) обращается в ноль Ех =![]() . Таким образом, две волны с равными амплитудами Eх(+) = Ezm(+) + Eym(+) и Eх(–) = Ezm(–) + Eym(–) вполне могут существовать, но их фазы и амплитуды таковы, что они полностью компенсируют проявления друг друга.
. Таким образом, две волны с равными амплитудами Eх(+) = Ezm(+) + Eym(+) и Eх(–) = Ezm(–) + Eym(–) вполне могут существовать, но их фазы и амплитуды таковы, что они полностью компенсируют проявления друг друга.
Точно так же можно добиться усредненного равенства нулю электрических векторов Еу=![]() и Еz=
и Еz=![]() , вращающихся соответственно в плоскостях XOZ и XOY.
, вращающихся соответственно в плоскостях XOZ и XOY.
Таким образом, внутренняя «жизнь» решимо может быть описана встречным вращением двух ортогональных базисов, состоящих из двух троек электрических векторов Ex(+),Eу (+), Ez(+) и Ex(–), Eу(–), Ez(–) с круговой поляризацией (рис. 3*** ***). При этом взаимно противоположное вращение двух ортогональных базисов должны в среднем полностью компенсировать проявления друг друга.
Циклическая скорость вращения W этих двух ортогональных троек электрических векторов (или электрических базисов) совпадает с угловыми частотами колебаний 3-х исследуемых (пробных) световых волн
Это связано с тем, что каждый электрический вектор Ei(±), определяющий одну из осей соответствующего электрического базиса, делает один полный оборот за один полный период колебания соответствующей световой волны. Это происходит потому, что модуль волнового вектора |ki| световых волн связан с их же угловыми частотами w i однозначным соотношением
| |ki | = w i /с. | (1н) |
Итак, вращение шестнадцати 3-базисов в рамках развиваемой теории связано с круговой поляризацией световых волн l mё n диапазона, высвечивающих исследуемый, согласованный объем (куб) l mё n -вакуума. Поэтому угловая скорость вращения dj /dt = W шестнадцати 3-базисов показанных на рис.3 в данной теории совпадает с циклической частотой пробных световых волн w c = 2p с /l mё n.
Таким образом, в рассматриваемой модели постулируется соотношение
| W =w c или dj /dt = 2p с /l mё n. | (1о) |
Откуда определяем два направления локального времени
| j l mё n /2p с = t | (1п) |
– в случае круговой поляризации пробных волн по часовой стрелке, и
| j l mё n /2p с = – t | (1р) |
– в случае круговой поляризации пробной волны против часовой стрелки.
При j = 2p (что соответсвует проходу луча света растояния равного полной длине свойей средней волны <l mё n> ) и положив e =|dr| =<l mё n> (где |dr| =|dx + dy + dz|) из (1п) получим векторное выражение со стигнатурой {– + + +} (понятие стигнатура будет введено несколько позже)
| ds(+)= – cdt + dx + dy + dz = 0, | (1с) |
а при подстанвке j = 2p в (1р) — векторное выражение со стигнатурой {+ – – –}
| ds(–) = cdt – dx – dy –dz = 0. | (1т) |
Все выделенные курсивом манипуляции произведены с целью показа, что в рамках рассматриваемой модели все шестнадцать 3- базисов (см. рис. 3) вращаются с угловой скоростью W равной средней циклической частоте w c пробных световых волн, «высвечивающих» согласованный куб lmё n -вакуума.
С учетом двух различных направлений вращения 3-базисов согласованного куба lmёn -вакуума удобно перейти к рассмотрению 4-базисов
| ei(a) (e0(a), e1(a), e2(a), e3(a)) = ei(a) (cdt, dx, dy, dz). | (1ф) |
где базисный вектор e0(a) – задает направление и темп локального времени, т. е. направление и угловую скорость вращения а-го 3-базиса (а = 1,2,3,…, 16)
Отметим, что векторный (электродинамический) анализ исследуемого объема l mё n -вакуума не приводит к согласованной картине вращений всех шестнадцати 4-базисов в комплексе. Как будет показано ниже, к такой удивительно гармоничной картине приводит кватернионный анализ 4-мерной протяженности l mё n -вакуума. Поэтому для данного класса задач кватернионный анализ оказался значительно более предпочтительным.
Вращательное движение, как и любой другой вид движения, сопряжено с внесением понятия стрелы времени направленной из прошлого в будущее. Время выступает как мера длительности, в течение которой осуществляется движение (в частности вращение). Но в силу того, что вращение 3-базисов может осуществляться как в одну, так и в противоположную сторону, то нам следует различать два направления локального времени. Поэтому будем считать, что восемь 3-базисов, показанных на рис. 3 а, вращаются по «часовой стрелке» и их стрела времени условно направлена «вверх». А восемь 3-мерных базисов, показанных на рис. 3 б, вращаются против «часовой стрелки», и их стрела времени условно направлена «вниз».
Таким образом, локальное время любого из шестнадцати 3-базисов оказывается неким аксиальным вектором, величина и направление которого тесно связанны с угловой скоростью и направлением вращения данного 3-базиса. Следовательно, для модели согласованного объема l mё n-вакуума, учитывающей гармоничное вращение всех шестнадцати, окаймляющих его 3-базисов (см. рис.3), удобно перейти к 4-меному рассмотрению.
Если условно ввести четыре оси сt = x0 , x = x1 , y = x2 , z = x3.(см. рис. 4), то в рамках 4-менного рассмотрения согласованный объем (куб) l mё n -вакуума со стороной e (см. рис.2) может быть наиболее полно описан шестнадцатью 4-базисами, представленными на рис. 5.
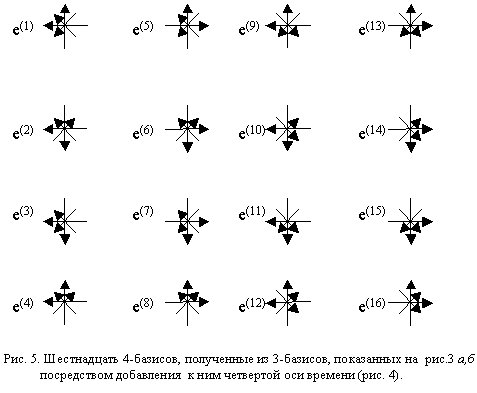
Существует придание, что ортогональная система координат пришла на ум Рене Декарту, кода он в тюрьме обдумывал суть природных явлений. Однажды Декарт увидел удаленное дерево через решетку окна своей камеры и сразу сообразил, что место положение этого дерева можно задать в виде проекций на оси двух перекрещенных осей отсчета. Но думаю, что глубинная основа ортогональных систем отсчета все же кроется в Распятье Спасителя, Положившему начало новой эры эмпирического познания Естества.
Для дальнейшего изложения нам понадобилось ввести три новых понятия: «решимо», «база» и «стигнатура».
Сначала введем понятие «решимо». Решимо (память, отпечаток) – это исходное совершенно не искаженное абсолютное псевдоевклидово пространство, описываемое системой ортогональных осей сt = x0 , x = x1 , y = x2 , z = x3. В этом идеальном пространстве не заданы никакие направления, т. е. все направления в нем равноправны.
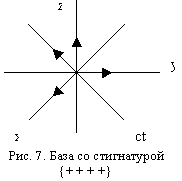
Выберем из шестнадцати 4-базисов, показанных на рис.5, пятый 4-базис ei(5) (e0(5), e1(5), e2(5), e3(5)) в качестве «базы» и условно примем, что направления всех его единичных базисных векторов данной «базы» положительны, т. е.
| ei(5) (e0(5), e1(5), e2(5), e3(5)) = (1, 1, 1, 1) ® {+ + + +}. | (2) |
Здесь введено обозначение {+ + + +}, означающее знаки, стоящие перед соответствующими модулями единичных векторов (+1, +1, +1, +1) пятого 4-базиса.
В дальнейшем обозначения (1, 1, 1, 1) и {+ + + +} будем считать эквивалентными, а совокупность 4-х знаков в фигурных скобках {+ + + +} будем называть стигнатурой 4-базиса или 4-мерного аффинного пространства (рис. 7), в котором этот 4-базис задает исходные направления.
Напомним, что аффинным называется такое пространство, на котором задана аффинная геометрия. Как известно, все теоремы аффинной геометрии справедливы в геометрии Евклида. Однако многих евклидовых теорем в аффинной геометрии нет (за подробностями отсылаем к специальным изданиям). В частности теорема Пифагора в ней отсутствует, т. к. углы в аффинной геометрии неинвариантны, следовательно, нет смысла говорить о прямоугольных треугольниках. Из-за отсутствия теоремы Пифагора в аффинной геометрии в ней не может быть задана квадратичная форма, играющая роль метрики в евклидовой геометрии.
Другими словами если в псевдо-евклидовом пространстве, например, с сигнатурой (– + + +), метрика задается квадратичной формой ds2 = – с2dt2 + dx2 + dy 2 + dz 2, то в аффинном пространстве с аналогичной стигнатурой {– + + +} роль метрики играет интервал ds = – с dt + dx + dy + dz. Сразу отметим, что сигнатура (– + + +) – это знаки, стоящие перед слагаемыми квадратичной формы евклидова пространства. А стигнатура {– + + +} – это знаки, стоящие перед слагаемыми интервала аффинного пространства. Сигнатуры мы будем помещать в круглые скобки, стигнатуры в – фигурные.
У решимо (рис.6) нет никаких выделенных направлений, т. е. ei(0) (e0(0), e1(0), e2(0), e3(0)) = (0, 0, 0, 0), поэтому стигнатуру решимо можно положить равной {0000}.
Положительные направления «базы» (рис.7) выбраны совершенно условно. В качестве исходного 4-базиса можно было бы выбрать любой из шестнадцати 4-базисов, показанных на рис. 5. Следовательно, в стигнатурном смысле протяженность Вселенной должна полностью симметричной.
Относительно выбранной «базы» (т. е. пятого 4-базиса) все остальные 4-базисы, показанные на рис.5, имеют следующие направления базисных векторов (т. е. стигнатуры):
ei(1)(e0(1),e1(1),e2(1),e3(1))=
|
ei(9)(e0(9),e1(9),e2(9),e3(9))=
|
Важно, что 16 стигнатур, приведенные в табл. 1, объединяются в антисимметричную матрицу:
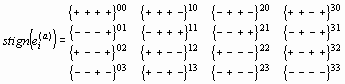 |
(3) |
Как выяснится ниже, эти 16 стигнатур образуют группу по операции ранжирного умножения.
В частности из-за того, что стигнатуры образуют антисимметричную матрицу (3) где {….}ab = – {….}ba действенными оказываются только 10 из 16 стигнатур.
Шестнадцать базисов, сведенные в табл. 1, показывают, что развиваемые здесь свето-геометрические представления о метрико-динамических свойствах согласованного объема l mё n-вакуума сродни алгебре квадрочисел веденной для описания одной из разновидностей финслерова пространства [2].
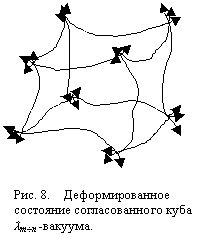
Рассмотрим теперь деформированное состояние исследуемого согласованного куба l mё n -вакуума. Пусть теперь «идеальный» куб l mё n -вакуума, показанный на рис. 3, приходит в деформированное состояние (см. рис.8). При этом оси всех 16 систем отсчета, связанные с вершинами и ребрами исследуемого куба, становятся, в общем случае, криволинейными xў 0(а), xў (а), xў 2(а), x3ў (а), а их 4-базисы eў i(a) (eў 0(a), eў 1(a), eў 2(a), eў 3(a)) – не ортогональными.
Свето-геометрия изначально исходит из того, что каждое ребро исследуемого согласованного куба l mё n -вакуума (рис. 3) получается с помощью луча света соответствующего диапазона длин волн. Таким образом, для того чтобы вырисовать исследуемый куб l mё n -вакуума необходимо 12 лучей — каждый луч соответствует одному из ребер согласованного куба.
На 4-искривленном участке l mё n -вакуума все пробные лучи света будут искривлены, т. к. лучи свет распространяется по геодезической линии, повторяющей 4-девормированный ландшафт исследуемого участка l mё n -вакуума. Поэтому в данном случае согласованный «куб» l mё n -вакуума будет искаженным (рис.8).
Если искривления осей xў 0(а), xў 1(а), xў 2(а), x3ў (а) (т. е. ребер куба) достаточно гладкое, то эти оси и их базисные вектора eў 0(a), eў 1(a), eў 2(a), eў 3(a) (рис. 6.7) всегда можно выразить через оси x0(а), x1(а), x2(а), x3(а) и базисные вектора e0(a), e1(a), e2(a), e3(a) исходного, идеального куба (рис. 6.4) с помощью преобразований
|
xў 0(а) = α00 (а)x0(а) +α01 (а)x1(а) +α02 (а)x2(а) +α03 (а)x3(а); xў 1(а) = α10 (а)x0(а) +α11 (а)x1(а) +α12 (а)x2(а) +α13 (а)x3(а); xў 2(а) = α20 (а)x0(а) +α21 (а)x1(а) +α22 (а)x2(а) +α23 (а)x3(а); x3ў (а) = α30 (а)x0(а) +α31 (а)x1(а) + α32 (а)x2(а) +α33 (а)x3(а) |
(4) |
и
|
eў 0(a) = β00 (a) e0(a) +β01 (a) e1(a) +β02 (a) e2(a) +β03 (a) e3(a); eў 1(a) = β10 (a) e0(a) +β11 (a) e1(a) +β12 (a) e2(a) +β13 (a) e3(a); eў 2(a) = β20 (a) e0(a) +β21 (a) e1(a) +β22 (a) e2(a) +β23 (a) e3(a); eў 3(a) = β30 (a) e0(a) +β31 (a) e1(a) +β32 (a) e2(a) +β03 (a) e3(a). |
(5) |
Или в более компактном виде
| xў i (a) = αij (a) xj (a) | (6) |
и
| eў i(a) = βij (a) ej (a), | (7) |
где
| αij (a) = dxў i(a)/ dxj (a) | (8) |
– якобианы преобразования;
| βij (a) = (eў i(a) Ч ej(a)) = cos (eў i(a) ^,ej(a)) | (9) |
– направляющие косинусы.
Преобразование (6), по сути, означает проекцию искривленных осей xў 0(а), xў 1(а), xў 2(а), x3ў (а) на идеальные оси решимо x0(а), x1(а), x2(а), x3 (а). А преобразование (6.344) – проекция неортогональных базисных векторов eў 0(a), eў 1(a), eў 2(a), eў 3(a) на ортогональные вектора исходного (идеального) 4-базиса e0(a), e1(a), e2(a), e3(a).
При этом каждый из шестнадцати искаженных 4-базисов, закрепленных в вершинах деформированного согласованного объема l mё n -вакуума, определяет искривленное аффинное 4-пространство векторов
| dsў (a) = eў i(a) dxў i (a) , (где а = 1, 2, …, 8) | (10) |
или с учетом (6) и (7)
| dsў (a) = bim(a) em(a) αij (a) dxj(a) = kьт(a) en (a) dxj(a), | (11) |
где
| kmj(a)= bim(a) αij (a). | (12) |
Основное требование, которое накладывает Алсигна на аффинную геометрию векторов (10), описывающих искаженное состояние согласованного участка l mё n -вакуума, связано с принципом отсутственности. Этот принцип требует, чтобы все отклонения от исходного, идеального состояния в среднем компенсировали проявления друг друга. Следовательно, как и для в среднем гладкого и ровного участка протяженности l mё n -вакуума, любой элемент длины естественной протяженности должен в среднем равняться нулю
|
(13) |
То есть в каждый конкретный момент времени протяженность l mё n -вакуума как бы есть, а в среднем ее нет. То же принцип отсутственности требует, чтобы искривления всех шестнадцати 4-базисов, совпадающих с ребрами рассматриваемого согласованного куба l mё n -вакуума среднем компенсировали проявления друг друга.
В этом и явлено Великое Чудо Бытия. Этим и отличается представления, развиваемые в рамках Алсигны [1], от любой теории механического эфира, где механический эфир – есть среда, состоящая из огромной совокупности в принципе неуничтожимых частиц. В Алсигне l mё n -вакуум – это лишь устойчивая двухстороння иллюзия, чудом явленная из Бесконечной «Пустоты». Чудо в том, что эта в среднем совершенно скомпенсированная иллюзия на столько конкретна и устойчива, что мы ее воспринимаем как реальный, осязаемый Мир.
- 2.4.1. Развитие аффинных геометрий
Согласно развиваемых представлений l mё n -вакуум это многообразие, в каждой точке х0, х1, х2, х3 которого заданы 16 тетрад (т. е. 4-базисов) ei(a) (e0(a), e1(a), e2(a), e3(a)) (а = 1…16), со всеми 16 возможными стигнатурами (3) (т. е. направлениями 4-х ортонормированных векторов).
Каждый из шестнадцати 4-базисов определяет локальное аффинное пространство, для которого может быть развита своя геометрия с кручением. В частности, особый интерес представляет геометрия абсолютного параллелизма, развитая Р. Вайценбеком и Д. Витали, получившая продолжение в работах Г. И. Шипова в рамках теории физического вакуума [6].
Рассмотрим один из шестнадцати 4-базисов с любой из 16 стигнатур и переопределим его для конкретного рассмотрения ei(a) = еА (х0, х1, х2, х3), А = 0, 1, 2, 3 – номер орта рассматриваемого 4-базиса.
Согласно теореме Эйлера, бесконечно малые повороты ортов 4-базиса можно заменить одним поворотом на угол dc вокруг определенной оси, проходящей через начало рассматриваемого 4-базиса. Бесконечно малый поворот (в отличие от конечного поворота) можно задать вектором [6]
| dc = dc ec, | (13а) |
где вектор ec направлен вдоль мгновенной оси вращения 4-базиса. Это направление выбирается так, что если смотреть с конца вектора ec на неподвижную точку О, то поворот совершается против часовой стрелки (правая система отсчета). Бесконечно малое изменение векторов репера ec при повороте dc имеет вид
| deA = [dc eA]. | (13б) |
Разделив (13а) на dt, получим
| (13в) |
где w = dc /dt – трехмерная угловая скорость вращения системы отсчета относительно мгновенной оси.
В данной работе более не будем развивать аффинную геометрию абсолютного параллелизма, отправляя к источнику [6]. Отметим только, что в рамках этой геометрии определяется кручение Риччи
| (13г) |
где
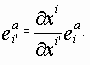
При переходе от аффинной геометрии к метрической вводится связность геометрии абсолютного параллелизма
| (13д) |
где
– символы Кристоффеля, здесь eja esb – скалярное произведение уже двух из шестнадцати 4-базисов как с одной и той же стигнатурой, так и с различными стигнатурами.
|
(13е) |
– коэффициента вращения Риччи, образованные взаимовращением любых двух из шестнадцати 4-базисов
Именно выражение (13е) Г. И. Шипов определил как торсионное поле (т. е. поле сил инерции возникающее в результате взаимовращения двух 4-базисов).
В отличие от работы Г. И. Шипова [6], где рассматривается взаимовращение только двух 4-базисов с одной и той же стигнатурой {+ – – –}, в Алгебре сигнатур имеет место 256 различных торсионных полей (13е), определенных для взоимовращения каждого из шестнадцати 4-базисов (табл. 1) с каждым же из них.
Таким образом, в Алсигне имеет место 16 аффинных геометрий с различными стигнатурами, которые порождают 256 метрических геометрий с различными топологиями.
Осуществим теперь переход от аффинных инферальных геометрий к метрическим инферальным геометриям. При этом будем разделять искривленные и неискривленные метрические пространства.
- 2.5.1. Неискривленные инферальные метрические подпространства
Перейдем теперь от шестнадцати аффинных геометрий с различными 4-базисами, в которых объектами рассмотрения являются в общем случае комплексные вектора (или комплексные функции), к 256 метрическим геометриям, исследующим квадратичные формы (метрики), и топологические свойства 256 «слоев» исследуемого l mё n -вакуума.
Метрическая геометрия базируется не на векторах (комплексных функциях), а на скалярном произведении векторов (квадратах модулей комплексных функций) при этом мы можем сравнивать длины не только параллельных прямых как в аффинной геометрии, но так же прямых, произвольно наклоненных по отношению друг к другу [4].
После того, как точа О (рис.2, 3) была препарирована в ней оказалось 16 систем отсчета (т. е. аффинных пространств) ка (x0(a), x1(a), x2(a), x3(a)) с соответствующими 4-базисами ei(a) (e0(a), e1(a), e2(a), e3(a)) (см. табл. 1).
С помощью скалярных произведений векторов, принадлежащим этим аффинным пространствам можно получить метрические протяженности с различными топологическими свойствами.
Пусть
| ds(a) = e i(a) dx i (a) = 0 | (14) |
– 4-вектор (интервал), заданный в системе отсчета ка (x1(a), x2(a), x3(a), x4(a)) с одними из 4-базисов ei(a) (e0(a), e1(a), e2(a), e3(a)), из табл. 1, а
| ds(b) = e i(b) dx i (b) = 0 | (15) |
– 4-вектор (интервал), заданный в другой системе отсчета кb (x1(b), x2(b), x3(b), x4(b)) с 4-базисом ei(b) (e0(b), e1(b), e2(b), e3(b)) из той же таблицы. Пусть, для примера, это будут системы отсчета с 4-базисами ei(5) (e0(5), e1(5), e2(5), e3(5)) и ei(7) (e0(7), e1(7), e2(7), e3(7)) (см. рис. 5 и рис. 9).
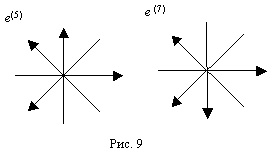
Начала отсчета систем ка и кb могут как совпадать с точкой О (рис. 2), так и не совпадать, т. е. находится в разных углах согласованного куба (рис.3). Для однородных и изотропных аффинных пространств это не имеет значения. Найдем теперь скалярное произведение 4-векторов (14) и (15)
| ds(5,7) 2 = ds (5) ds (7) = e i(5) e j(7) dxi (5) dx j (7). | (16) |
Оси координат x1(5), x2(5), x3(5), x4(5) и x1(7), x2(7), x3(7), x4(7) совпадают с осями координат решимо (рис.6), т. е. x0(5) = x0(7) = x0, x1(5) = x1(7) = x1, x2(5) = x2(7) = x2, x3(5) = x3(7) = x3. Поэтому выражение (16) можно представить в виде
| ds(5,7) 2 = ds (5) ds (7) = e i(5) e j(7) dxi dxj | (17) |
или в развернутом виде, с учетом ортогональности векторов 4-базисов ei(5) и ei(7), имеем
Откуда видим, что метрическое пространство, задаваемое квадратичной формой (метрикой) ds(5,7) 2, имеет сигнатуру (+ + + –).
Вместо скалярного произведения (17) может быть введена более компактная, эквивалентная запись, приводящая к той же сигнатуре, что и в метрике (17)
| {+ + + +} {+ + + –} (+ + + –)ґ, |
(18) |
где преумножаются знаки в одном столбце числителя, а результат такого перемножения записывается в этом же столбце, но в знаменателе ранжира (18). Умножение знаков производится по обычным арифметическим правилам:
| {+} ґ {+} = {+}; {-} ґ {+} = {-}; {+} ґ {-} = {-}; {-} ґ {-} = {+}. | (19) |
Такую запись будим называть ранжирным умножением, т. к. знаки здесь перемножаются по ранжиру (т. е. по столбцам). Знак умножения в индексе знаменателя данного ранжира (….)ґ, означает произведенную в числителе операцию. В данном случае операцию умножения. Далее в случае ранжирного деления стигнатур в числителе по обычным арифметическим правилам
| {+}: {+} = {+}; {–}: {+} = {–}; {+}: {–} = {–}; {–}: {–} = {+}. | (20) |
В знаменателе стигнатурного ранжира будем ставить индекс (….):. Например, запись
| {– + – +} {+ + + –} (– + – –): |
(21) |
Означает стигнатурное ранжирное деление.
По операциям ранжирного умножения и ранжирного деления 16 стигнатур:
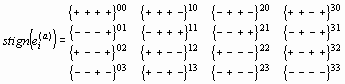 |
(22) |
образуют группу, что свидетельствует о наличии глубинных топологических симметрий в основаниях протяженности l mё n -вакуумов.
Если подобным образом скалярно перемножить между собой все 16 недеформированных систем отсчета с 4-базисами, показанными на рис. 5, то получим 16 ґ 16 = 256 метрических пространств с метриками
| ds(а, b) 2 = e i(а) e j(b) dxi(а) dxj (b) (a,b = 1,…,16), | (24) |
с различными сигнатурами.
Эквивалентные записи данных 256 скалярных произведений, подобно (21), могут быть представлены в виде 16 ґ 16 = 256 стигнатурных ранжирных умножений:
|
{+ – + +} |
{+ + + +} |
{– + + +} |
{+ + + +} |
|
{+ – – +} |
{+ + – +} |
{– + + +} |
{+ – + –} |
|
{+ – – –} |
{+ + – +} |
{– + – +} |
{+ – + +} |
|
… |
… |
… |
… |
|
{+ + + –} |
{– + – –} |
{– + + –} |
{+ – – +} |
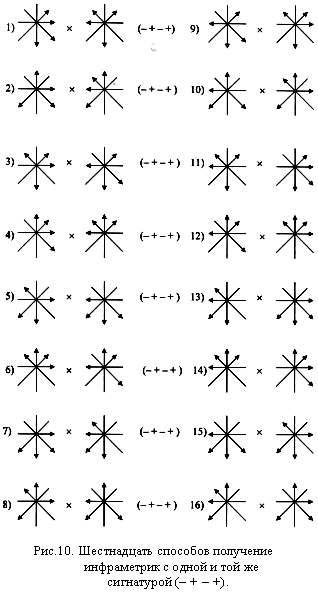
Метрики с различными сигнатурами типа (24)
ds(а, b) 2 = e i(а) e j(b) dxi(а) dxj (b),
будем иногда называть инфраметриками, а задаваемые ими 4-мерные метрические пространства – инферальными «4-картами» (т. е. поперечными 4-слоями исследуемого l mё n -вакуума). Суперпозиция (т. е. аддитивное наложение) всех 256 инферальных 4-карт образует «256-атлас», которым, по сути, и является изучаемым l mё n -вакуумом.
Метрические протяженности (инферальные 4-карты) с инфраметриками (24), имеющими, «ущербные» сигнатуры типа (– + – +) или (–+ – –), по отдельности не наблюдаемы. Но, как будет показано ниже, их суперпозиция (т. е. 256-атлас) приводит к двусторонней 4+4-мерной протяженности наблюдаемой реальности, внешняя сторона которой является мир Минковского с сигнатурой (– + + +), а её внутренней стороной – мир Минковского с сигнатурой (+ – – –).
Покажем, что сигнатур на самом деле не 256, а всего 265: 16 = 16. Каждая сигнатура может быть получена 16-ю способами, т. е. 16-ю скалярными произведениями ei(а) ej(b). Подтвердим это утверждение на примере сигнатуры (– + – +).
Рассмотрим все возможные скалярные произведения двух ортогональных 4-базисов ei(а) ej(b), приводящих к сигнатуре (– + – +) (см. рис. 10).
Таких скалярных произведений оказывается 16. Действительно, если два единичных вектора, принадлежащих одной и той же оси данных 4-базисов коллинеарные, то их скалярное произведение равно + 1, или просто (+); а если неколлинеарные, то – 1, или просто (–). Из комбинаторики известно, что число различных размещений n = 2 различных элементов (знаков + и –) в N = 4 различных ячейках (осях систем отсчета) равно Р = N n = 42 = 16.
Точно так же 16-ю различными скалярными произведениями может быть получено каждая из 16 сигнатур, представленных в матрице сигнатур
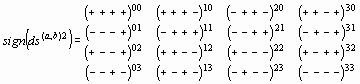 . . |
(25) |
Таким образом, сигнатуры, так же как стигнатуры, образуют антисимметричную матрицу (25)
sign (ds(а, b) 2) = – sign (ds(b, а) 2),
или
(….)ab = – (....)ba.
При этом действенными оказываются только 10 из 16 стигнатур.
- 2.5.2. Искривленные инферальные метрические подпространства
Для случая искривленного (деформированного) согласованного куба l mё n -вакуума (рис.8), интервалы (т. е. 4-векора) (14) и (15) будут теперь «искажены»
| ds(a)ў = e i(a)ў dx i(a)ў и ds (b)ў = ei(b)ў dx i(b) ў. | (26) |
При проектировании этих 4-векторов на решимо (подобно тому, как это делалось в п. 2.3) получим
dsў (a)= bin(a) en(а) αij (a) dxj(а) = kin(a) en(a) dxj(a) = kin(a) en(a) dxi |
(27) |
и
| dsў (b)= bim(b) em(b)α ij(b) dxj(b) = kjт(b) em(b) dxj(b) = kjт(b) em(b)dxj, | (28) |
где xj – координатные оси решимо;
en(a) – соответствующиеисходные ортогональные 4-базисы;
kin (a)= bjn(a) αij (a) – компоненты аффинного тензора а-го искривленного аффинного пространства;
kjm (b)= bim(b) αij (b) – компоненты аффинного тензора b-го искривленного аффинного пространства;
Найдем теперь скалярное произведение «искаженных» 4-векторов (27) и (28)
| dsў (a, b)2 = dsў (a)dsў (b) = kiт(a) kjn(b) en (a) em(b) dxj(a)dxj (b) = сji(a, b)dxj(a) dxj(b) = сji(a, b)dxj dxj, | (29) |
где xj – координатные оси решимо;
сji(a, b)= kiт(a) kjn(b) en(a) em (b) – компоненты инфраметрического тензора (a, b)-го искривленного инферального метрического подпространства.
Из (29) следует, что локальные искривления инферальных метрических подпространств полностью описываются произведениями компонентов kiт(a) kjn(b). При этом сигнатура (т. е. топологические свойства) искаженного участка (a, b)-го инферального метрических подпространства с инфраметрикой
| dsў (a, b)2 = сji(a, b)dxj(a)dxj (b) или dsў (k)2 = сji(k)dxj dxj, | (30) |
где 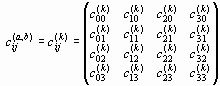 ; a,b = 1,…,16; k = 1,…,256. ; a,b = 1,…,16; k = 1,…,256. |
(31) |
так же как в (24) определяется скалярным произведением векторов en(a) em(b), принадлежащих ортогональным 4-базисам (см. рис.5). Поэтому топология искривленного k-го инферального метрические подпространства совпадает с топологией того же k-го неискривленного подпространства и определяется одной из 16-и возможных сигнатур
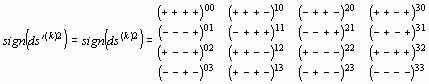 . . |
(32) |
- 2.5.3. Топологические свойства инферальных метрических подпространств
Выявим топологические свойства 256 инферальных метрических подпространств (4-карт) с инфраметриками (30) и различными сигнатурами (32). Наиболее ярко топологические свойства 4-карт выявляются в случае диагонального вида метрических матриц (31)
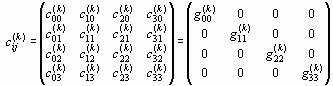 . . |
(33) |
Метрические матрицы квадратичных форм (31) всегда можно свести к диагональному виду, причем бесконечным количеством способов. Различные способы приводят к различным наборам диагональных элементов gij(k). Однако, как доказывается в алгебре матриц [3], число положительных, отрицательных и равных нулю коэффициентов gij(k) не зависит от способа приведения. Это свойство называется законом инерции квадратичных форм. По сути, закон инерции квадратичных форм означает, что любой способ приведения матриц (31) к диагональному виду оставляет сигнатуру инфраметрики 4-карты (30) неизменной. Поэтому исследование топологических свойств 4-карт на основании приведенных квадратичных форм, не только более наглядно, но и совершенно корректно.
Приведение матриц (31) к диагональному виду (33), позволяет записать инфраметрики (30) всех 256 инферальных метрических подпространств (4-карт) в упущенном виде
| dsў (k)2 = сij(k)dxi dx j = ± g00(k)dx0 2 ± g11(k)dx1 2 ± g22(k)dx2 2 ± g33(k)dx3 2 = 0. | (34) |
Для простоты избавимся так же в (34) от дифференциалов
| s(k)2 = ± g00(k)x02 ± g11(k) x12 ± g22(k) x22 ± g33(k) x32 = 0, | (35) |
поскольку топологические свойства бесконечно малых и глобальных участков протяженности 4-карты с одной и той же сигнатурой идентичны
Запишем все 16 возможных типов квадратичных форм (35) с одной из 16 возможных сигнатур (32):
|
g00(к)x02+g11(к)x12+g22(к)x22+g33(к)x32=0, (+ + + +) –g00(о)x02–g11(о)x12–g22(о)x22+g33(о)x32=0, (– – – +) g00(ж)x02–g11(ж)x12–g22(ж)x22+g33(ж)x32=0, (+ – – +) –g00(з)x02–g11(з)x12+g22(з)x22–g33(з)x32=0, (– – + –) g00(г)x02+g11(г)x12–g22(г)x22–g33(г)x32=0, (+ + – –) –g00(с)x02+g11(с)x12–g22(с)x22–g33(с)x32=0, (– + – –) g00(ф)x02–g11(ф)x12+g22(ф)x22–g33(ф)x32=0, (+ – + –) g00(б)x02–g11(б)x12–g22(б)x22–g33(б)x32=0, (+ – – –) метрика мира Минковского, (36) белый свет |
–g00(ак)x02–g11(ак)x12–g22(ак)x22–g33(ак)x32=0, (– – – –) g00(ао)x02+g11(ао)x12+g22(ао)x22–g33(ао)x32=0, (+ + + –) –g00(аж)x02+g11(аж)x12+g22(аж)x22–g33(аж)x32=0, (– + + –) g00(аз)x02+g11(аз)x12–g22(аз)x22+g33(аз)x32=0, (+ + – +) –g00(аг)x02–g11(аг)x12+g22(аг)x22+g33(аг)x32=0, (– – + +) g00(ас)x02–g11(ас)x12+g22(ас)x22+g33(ас)x32=0, (+ – + +) –g00(аф)x02+g11(аф)x12–g22(аф)x22+g33(аф)x32=0, (– + – +) –g00(ч)x02+g11(ч)x12+g22(ч)x22+g33(ч)x32=0, (– + + +) метрика изнанки мира Минковского, (37) черный свет |
Индексы в скобках указывают на условный цвет (окраску) инферального метрического подпространства с соответствующей инфраметрикой (сигнатурой): к – красный; о – оранжевый; ж — желтый; з – зеленый; г – голубой; с – синий; ф – фиолетовый; б – белый. ак – анти-красный; ао – анти-оранжевый; аж – анти-желтый; аз – анти-зеленый; аг – анти-голубой; ас – анти-синий; аф – анти-фиолетовый; ч – черный. При этом охватывается вся цветовая гамма белого и черного света.
Белый свет с сигнатурой (+ – – –) является суперпозицией 7-ми светов с различными (цветными) сигнатурами в числителе ранжира (36). Черный свет с сигнатурой (– + + +) является суперпозицией 7-ми светов с различными (антицветными) сигнатурами в числителе ранжира (37).
Отметим, что здесь обнаруживаются признаки суперсимметрии между 4-пространством и полем. С одной стороны 16 квадратичных форм (36) и (37) описывают распространение лучей света различного качества подобно интервалам ds(+)2= – c2dt 2 + dx2+ dy2+ dz 2= 0 или ds(–)2 = c2dt 2 – dx2 – dy2– dz 2= 0. С другой сторны, эти же квадратичные формы (36) и (37) описывают протяжности 4-карты с различными топологическими свойствами.
Метрики всех шестнадцати видов 4-карт (36) и (37) можно разбить на три основных класса.
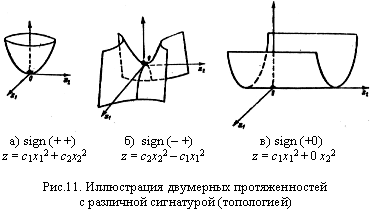
1 класс: 4-карты с сигнатурами (+ + + +) и (– – – –) – называются «нулевыми поверхностями». Данный тип 4-мерных поверхностей характеризуется тем, что их сигнатуры состоят только из одинаковых знаков.
|
Класс 1 |
|
|
2 класс: 4-карты с сигнатурами (– – – +); (– – + –); (– + – –); (+ – – –), и их антиподы с сигнатурами (+ + + –); (+ + – +); (+ – + +); (– + + +) – называются «овальными поверхностями». Второй класс характеризуется наличием 3-х одинаковых знаков и 1-го противоположного знак в сигнатуре.
|
Класс 2 |
|
овальные поверхности: а) эллипсоиды; б) эллиптические параболоиды; с) двуполостные гиперболойды. Овальные поверхности характеризуются тем, что в их сигнатурах содержится только один отличный от других знак. 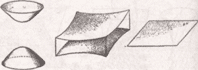 |
3 класс: 4-карты с сигнатурами (+ – – +); (+ + – –); (+ – + –), и их антиподы с сигнатурами (– + + –); (– – + +); (– + – +) – называются кольцеобразными поверхностями. В этом классе в сигнатурах присутствует по два одинаковых знака).
|
Класс 3 |
|
Кольцеобразные (или тороидальные) поверхности. У кольцевых поверхностей сигнатуры содержат по два положительных и по два отрицательных знака. 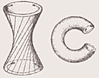 |
Каждая инфраметрика (квадратичная форма) dsў (k)2 = сji(k)dxj dxj = 0 задает одну из 256 инферальных метрических подпространств (4-карт) с соответствующей ей сигнатурой, а следовательно и топологией.
Инферальные метрические подпространства (4-карты) с квадратичными формами типа (38) – (40) образуют атлас с 256-ю «листами», на которые расслаивается протяженность любого l mё n -вакуума.
Таким образом, вся бездонная толща протяженности Великого Вакуума расщепляются на иерархию продольных слоев – т. е. l mё n -вакуумы с различными масштабными факторами. А сами l mё n-вакуумы в свою очередь расщепляются на поперечны, инферальные слои – 4-карты с различными сигнатурами (топологиями).
Упрощенная иллюстрация влияния сигнатуры на топологию 2-мерной протяженности показана на рис.11. На этом рисунке приведены двухмерные метрические поверхности с различными сигнатурами (топологиями).
2.5.4. Физическая интерпретация, развиваемого математического аппарата свето-геометрии
В классической теории упругости актуальное состояние выделенного куба любой упруго-пластичной среды, как плавило, описывается только одной «вмороженной» в нее системой отсчета, что в итоге приводит к анализу изменений только одной квадратичной формы
| dsў 2 =сji dx j dx j, | (41) |
которую сравнивают с квадратичной формой
| ds02 = с0ijdx i dx j, | (42) |
описывающей идеальное (исходное) состояние того же локального участка упруго-пластической среды.
Вычитая метрику исходного состояния из метрики актуального состояния
| (43) |
определяют тензор деформаций
| (44) |
который и является предметом изучения классической теорий упругости.
Отличие представлений, развиваемой здесь алгебры сигнатур (Алсигны), заключается лишь в том, что исследуемый участок (куб) упруго-пластической среды описывается не одним базисом, связанным с одним из восьми углов исследуемого куба, а с 16-ю базисами – по два в каждом углу данного куба (см. рис.12).
Данное обстоятельство привод к тому, что вместо одной метрики (42), в алгебре сигнатур фигурирует 256 инфраметрик
с различными сигнатурами. При этом не только значительно более точно осыпаются деформации следуемого участка упруго-пластической среды, но и вскрывается внутренняя структура пространства.
Вместо девяти или шестнадцати чисел (компонент метрического тензора), фигурирующих в обычных 3-х и 4-х мерных теориях упругости, Алсигна описывает актуальное состояние исследуемого объема 256 ґ 16 = 4096 числами (компонентами инфраметрических тензоров) сji(a, b). Откуда видим, что Алсигна предоставляет значительно более мощный и точный математический аппарат для исследования метрико-динамических свойств различных упруго-пластических сред и в частности l mё n -вакуумов.
Продолжение следует
- Козлов А. И., Логвин А. И., Сарычев В. А. Поляризация радиоволн. – М.: Радиотехника, 2005.
- Павлов Д. Г. Обобщение аксиом скалярного произведения. // Гиперкомплексные числа в геометрии и физике №1. 2004.
- Клиот-Дашинский М. И. Алгебра матриц и векторов. – С-Пб.: Лань, 2001.
- Грин Б. Элегантная Вселенная. – М: УРСС, 2004.
- Клейн Ф. Неевклидова геометрия. – М: УРСС, 2004.
- Шипов Г. И. Теория физического вакуума. – М.: Наука, 1997.
- Гаухман М.Х. Алгебра сигнатур. – М.: Издатель Гаухман М.Х., 2004.
- Пенроуз Р. Структура пространства-времени. – Череповец: Меркурий-пресс, 2000.
- Ландау Л.Д., Лифшиц Е.М. Теория поля. – М.: Наука, 1988. –Т.2.
Батанов М. Свето-геометрия Вакуума // «Академия Тринитаризма», М.,
|
|