|
|
|
Абнер Шимони
Реальность квантового мира
МЫ ЖИВЕМ в замечательную эпоху, когда философские проблемы наконец находят свое разрешение на основе экспериментальных результатов. Ни в одной области науки не было получено столь захватывающих результатов, как в квантовой механике. Начиная с 20-х годов эта теория неоднократно подтверждалась в экспериментах. Великолепно оправдались ее предсказания относительно многих явлений атомной, молекулярной и ядерной физики, оптики, физики твердого тела и элементарных частиц. Однако законы квантовой механики причудливы и не находят опоры в наших интуитивных представлениях, почерпнутых из обыденной практики. Поэтому, невзирая на успехи квантовой механики, многие ученые, в том числе и Эйнштейн, полагали, что квантово-механическое описание физических систем неполно, что к нему необходимо еще что-то добавить. Недавно проведенные эксперименты приводят к выводу, что такое мнение, скорее всего, ошибочно. Полученные результаты отчетливее чем когда-либо показывают, что мы живем в странном «квантовом мире», не поддающемся интерпретации на основе очевидного здравого смысла.
Вот несколько новых необычных выводов, справедливость которых мы вынуждены признать. Во-первых, два объекта, разделенных многометровым расстоянием и никак между собой не связанных, тем не менее «чувствуют» присутствие друг друга. Их поведение поразительным образом скоррелировано, так что измерения, выполненные над одним из них, мгновенно влияют на результаты измерений, выполняемых над другим. Этот вывод невозможно объяснить с точки зрения классической науки, но он полностью согласуется с квантовой механикой. Во-вторых, фотон — квант электромагнитного излучения — может вести себя и как частица, и как волна. В таком неопределенном состоянии он существует до тех пор, пока над ним не проведут какого-то физического измерения. Если при этом измеряются частицеподобные характеристики, то фотон предстанет перед нами частицей; если будут измеряться его волновые характеристики, то он будет вести себя подобно волне. Пока не указаны условия эксперимента, невозможно сказать, является ли фотон волной или частицей. Наконец, идея квантовых неопределенностей вышла за пределы атомного и субатомного мира. Ученые обнаружили, что при некоторых условиях макроскопические системы существуют в таком состоянии, когда наблюдаемые макроскопические величины не имеют определенного значения. Каждый из этих выводов коренным образом изменяет представления об окружающем нас мире.
ЧТОБЫ понять суть проведенных экспериментов и оценить их влияние на философские концепции, нужно хотя бы бегло познакомиться с основными идеями квантовой механики. При любом обсуждении этой теории самым существенным понятием является квантовое состояние, описываемое волновой функцией. Конкретное квантовое состояние определяет все численные характеристики физической системы в той степени, в какой это вообще можно сделать. Последняя оговорка крайне важна, так как, согласно квантовой механике, не все характеристики системы могут одновременно иметь определенные значения. Так, известный принцип неопределенности Гейзенберга гласит, что частица не может занимать определенное положение и иметь при этом определенный импульс. Это, возможно, самый известный пример приведенного выше утверждения.
В квантовой механике ясно и недвусмысленно можно говорить лишь о вероятностях каждого возможного исхода конкретного эксперимента, выполняемого над системой, находящейся в данном квантовом состоянии. Если эта вероятность оказывается равна единице, то результат эксперимента предопределен. Если она оказывается равной нулю, то данный исход эксперимента невозможен. Но если вероятность заключена между единицей и нулем, то заранее нельзя сказать, каков будет исход каждого отдельного эксперимента. В таком случае можно предсказать лишь среднее число для результатов, если один! и тот же эксперимент выполняется над большим числом идентичных систем.
Представим себе, что мы проводим: измерения с фотоном. Квантовое состояние фотона фиксируется тремя величинами: направлением распространения, частотой и линейной поляризацией (т. е. направлением вектора электрического поля, связанного с фотоном). Подходящим прибором для измерения поляризации является так называемая поляризующая пленка. Если свет линейно поляризован вдоль некоторого направления на пленке, которое называется оптической осью, то идеальная пленка полностью пропустит его. Если же поляризация перпендикулярна этой оси, то свет будет поглощен. (Здесь и далее имеется в виду, что свет падает на пленку под прямым углом.)
Вращая пленку, можно поставить ряд экспериментов. Если свет поляризован вдоль оптической оси, то вероятность его прохождения через пленку равна единице. Если свет линейно поляризован перпендикулярно оси, то вероятность его прохождения равна нулю. Мы не обсуждали еще случая, когда фотон линейно поляризован в направлении, составляющем некоторый угол с оптической осью. Тогда вероятность прохождения света есть число между нулем и единицей (точнее, квадрат косинуса этого угла). Если, скажем, угол равен 45°, то вероятность прохождения равна 1/2. Это означает, что из 100 фотонов, линейно поляризованных в данном направлении, в среднем только 50 пройдут сквозь пленку.
Другая основная идея квантовой механики — принцип суперпозиции, согласно которому из любых двух квантовых состояний системы можно получить другие состояния, представляющие «смесь» первых двух. Физически такая операция сводится к получению состояния, которое «перекрывает» каждое из исходных состояний. Идею можно проиллюстрировать на примере двух квантовых состояний фотона, в которых направления линейной поляризации взаимно перпендикулярны. Из них можно получить несколько квантовых состояний, также имеющих линейную поляризацию, направление которой, однако, составляет произвольный угол по отношению к направлениям поляризации исходных состояний.
УЖЕ ТОЛЬКО из двух основных идей — принципа неопределенности и принципа суперпозиции — становится ясно, что квантовая механика в сильной степени противоречит так называемому здравому смыслу. Если квантовое состояние системы дает ее полное описание, то величина, не имеющая в данном состоянии определенного значения, не просто неизвестна ученому, стремящемуся описать эту систему. Неопределенность этой величины носит объективный характер. Кроме того, поскольку исход эксперимента по измерению объективно неопределенной величины не детерминирован квантовым состоянием, а последнее является носителем полной информации о системе, этот исход принципиально случаен. Случаен даже не в смысле его непредсказуемости ученым. Вероятность каждого возможного исхода измерения есть объективная вероятность. Классическая физика не вступает в столь разительное противоречие со здравым смыслом.
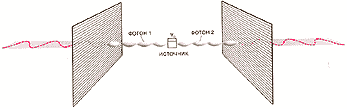
Еще к более поразительным выводам приводит квантовая механика при описании системы, состоящей из двух удаленных друг от друга частей. Представим себе два фотона, разлетающихся в противоположных направлениях. Одно из возможных квантовых состояний этой системы есть состояние, в котором фотоны поляризованы вдоль вертикальной оси. Другое возможное состояние — поляризация обоих фотонов вдоль горизонтальной оси. Нет ничего странного или удивительного в таких двух-фотонных квантовых состояниях, за исключением уже обсуждавшихся особенностей, присущих однофотонным состояниям. Но если принять во внимание принцип суперпозиции, то могут возникнуть необычные эффекты.
В частности, используя принцип суперпозиции, можно получить смешанное состояние, содержащее равные вклады вертикально и горизонтально поляризованных состояний. Такое состояние нам еще неоднократно встретится в дальнейшем, поэтому мы обозначим его ψ0 (так как греческая буква «пси» обычно используется для обозначения квантовых состояний). Свойства ψ0 на самом деле удивительны. Например, представим, что на пути фотонов помещены поляризующие пленки, оптические оси которых направлены вертикально. Поскольку ψ0 содержит равное число вертикально и горизонтально поляризованных состояний, вероятность прохождения обоих фотонов через поляризующие пленки будет равна 1/2. Вероятность того, что оба они будут задержаны, также равна 1/2. Такого просто не может случиться, чтобы один фотон прошел, а второй был бы задержан пленкой. Иными словами, имеется сильная корреляция результатов экспериментов с двумя разными фотонами.
Такая же ситуация будет иметь место, если пленки расположены под углом 45° к горизонтали: либо оба фотона пройдут сквозь пленку, либо оба будут задержаны. Только один фотон пройти через пленку не может. В действительности результаты поляризационных экспериментов не зависят от ориентации пленок, при условии что они одинаковы. Таким образом, можно указать бесконечное множество поляризационных экспериментов, результаты которых сильно коррелируют. (Конечно, на практике можно выполнить только один из них.) Каким-то образом второй фотон в паре «знает», проходить ему через пленку или нет в соответствии с тем, прошел или не прошел первый фотон. При этом оба фотона могут находиться на значительном расстоянии друг от друга, и ни у одного из них нет механизма передачи информации другому. В подобных ситуациях квантовая механика бросает вызов релятивистской концепции локальности, согласно которой никакое воздействие не может передаваться со скоростью, превышающей скорость света (в частности, невозможно мгновенное действие на расстоянии).
СЛЕДУЕТ подчеркнуть, что все обсуждавшиеся выше особенности квантовомеханических законов — объективные неопределенность, случайность, вероятность и нелокальность — существенно зависят от предположения о том, что квантовое состояние системы дает ее полное описание. Некоторые теоретики считают, однако, что квантовое состояние просто описывает ансамбль одинаково полученных систем, и потому хорошие предсказания могут быть сделаны только относительно статистических результатов одного и того же эксперимента, выполняемого над всеми системами, входящими в ансамбль. В то же время, утверждают они, каждый член ансамбля отличается от других чем-то, что не находит отражения в их квантовом состоянии. Поэтому и различаются результаты отдельных экспериментов. Свойства индивидуальных систем, не описываемые квантовым состоянием, определяются так называемыми скрытыми параметрами.
Если правы теоретики, придерживающиеся идеи скрытых параметров, то объективной неопределенности не существует. Тогда дело просто в том, что ученые не знают значений скрытых параметров, характеризующих рассматриваемую индивидуальную систему. Далее, не существует объективной случайности и объективной вероятности. Самое важное то, что факт корреляции свойств разделенных систем становится не более удивительным, чем совпадение двух экземпляров одной и той же газеты, напечатанных в одной типографии, но разосланных по почте в разные города.
В 1964 г. Дж. Белл из Европейской организации ядерных исследований (ЦЕРН) в Женеве показал, что предсказания локальных моделей со скрытыми параметрами несовместимы с предсказаниями квантовой механики. Размышления над некоторыми моделями со скрытыми параметрами, которые развивались Д. Бомом из Беркбек-Колледжа в Лондоне и Л. де Бройлем, привели Белла к доказательству важной теоремы. Суть ее в том, что ни одна модель, обладающая свойством локальности (в строго определенном смысле), не может быть согласована со статистическими предсказаниями квантовой механики. Иными словами, имеются физические ситуации, в которых предсказания квантовой механики будут отличаться от предсказаний любой локальной модели со скрытыми параметрами (см. Bernard d'Espagnat. The Quantum Theory and Reality, «Scientific American», November, 1979).
Идею Белла можно представить, по крайней мере частично, обратившись вновь к квантовому состоянию ψ0. Как было отмечено выше, результаты поляризационных экспериментов над парой фотонов в этом состоянии должны сильно коррелировать между собой, если угол между оптическими осями поляризационных пленок равен нулю (например, когда обе оси направлены вертикально). Не должен вызвать особого удивления и тот факт, что по крайней мере частичная корреляция результатов измерений будет иметь место при любом угле между осями пленок. (Точнее, если один из фотонов проходит через пленку, то вероятность прохождения второго фотона равна квадрату косинуса угла между оптическими осями пленок.)
Соответственно в моделях со скрытыми параметрами (которые согласовывались бы со всеми статистическими предсказаниями квантовой механики) каждой паре фотонов в ансамбле должны быть приписаны значения параметров столь тонким образом, чтобы была обеспечена сильная или частичная корреляция измерений при любом угле между оптическими осями пленок. Но условие локальности требует, чтобы значения параметров, приписываемые каждому фотону в паре, не зависели от ориентации пленки, на которую падает другой фотон, и от того, пройдет он сквозь пленку или задержится. Именно требования локальности делают невозможной тонкую «регулировку», необходимую для воспроизведения сильной и частичной корреляции, следующей из квантового состояния ψ0.
ТАКИМ образом, теорема Белла утверждает, что в принципе экспериментально можно определить, какая из теорий верна: квантовая механика или локальные модели со скрытыми параметрами. Такие опыты были важны хотя бы потому, что, несмотря на огромное число подтверждений квантовой механики, к моменту, когда Белл привел доказательство своей теоремы, не были проверены именно те узловые моменты, где квантовая механика несомненно вступает в противоречие со здравым смыслом.
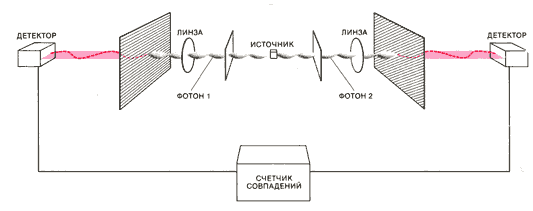
В 1969 г. Дж. Клаузер (работавший тогда в Колумбийском университете), М. Хорн из Бостонского университета, Р. Хольт из Гарвардского университета и я предложили проект соответствующего эксперимента. Пары фотонов с коррелированными линейными поляризациями должны были получаться путем возбуждения атомов до нужного начального состояния. При последующем возвращении в невозбужденное состояние атомы должны были излучать по два фотона. С помощью фильтров и линз можно было добиться того, чтобы при разлетании фотонов в противоположных направлениях один из них падал на первый поляризационный анализатор, а другой — на второй. Изменяя относительную ориентацию анализаторов и регистрируя число фотонных пар, прошедших через них при четырех возможных комбинациях относительного расположения, можно было измерить корреляцию в прохождении фотонных пар.
Мы предложили использовать в качестве поляризационных анализаторов кристаллы кальцита или стопки зеркального стекла, которые гораздо более эффективно задерживают фотоны, поляризованные в направлении, перпендикулярном оптической оси, чем обычные поляризующие пленки. За анализаторами помещались фотодетекторы, регистрирующие определенную долю проходящих фотонов. Если каждый детектор зарегистрирует фотон, причем время между регистрацией не превысит 20 нс (1 нс = 10 -9 с), то вероятность того, что оба фотона были испущены одним и тем же атомом, будет велика. Поскольку линзы собирают пары фотонов, испущенных в некотором конечном интервале углов, квантовое состояние фотонов не совпадает точно с квантовым состоянием ψ0, а представляет собой несколько модифицированное состояние ψ0, в котором также имеют место корреляции, не воспроизводимые никакой локальной моделью со скрытыми параметрами.
Такой эксперимент был выполнен в 1972 г. С. Фридманом и Клаузером в Калифорнийском университете в Беркли, Э. Фрайем и Р. Томпсоном в Техасском университете в 1975 г. и после этого еще рядом других групп. Большая часть экспериментальных результатов согласуется с предсказаниями корреляций на основе квантовой механики и несовместима с предсказаниями моделей со скрытыми параметрами. Кроме того, под сомнение была поставлена достоверность тех экспериментов, где были получены другие результаты, так как обнаружились слабые места в методике их проведения.
Тем не менее до недавнего времени все эксперименты оставляли возможность, позволявшую сторонникам скрытых параметров еще на что-то надеяться. Дело в том, что поляризационные анализаторы сохраняли свою относительную ориентацию примерно в течение минуты, что вполне достаточно для обмена информацией между ними с помощью какого-нибудь гипотетического механизма. В результате сторонники скрытых параметров могли утверждать, что из специальной теории относительности в конкретных условиях данных экспериментов еще не следует выполнение требования локальности Белла. Поэтому такие опыты нельзя рассматривать как критические эксперименты, устанавливающие справедливость квантовой механики или моделей со скрытыми параметрами.
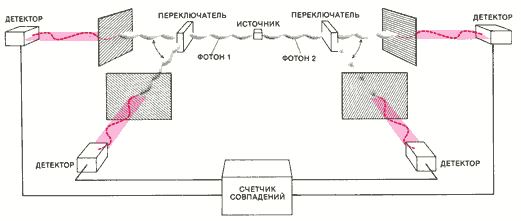
ЧТОБЫ исключить и эту возможность, А. Аспект, Ж. Далибар и Ж. Роже из Оптического института Парижского университета выполнили эффектный эксперимент, в котором выбор ориентации поляризационных анализаторов производится оптическими переключателями во время полета фотонов. Эксперимент потребовал восьми лет работы и был закончен только в 1982 г. Каждый переключатель представляет собой небольшой сосуд с водой, в котором ультразвук периодически возбуждает стоячие волны. Эти волны играют роль дифракционной решетки, которая может весьма эффективно отклонять падающие фотоны. При возбуждении стоячей волны фотон отклоняется на анализатор с одной ориентацией, а при «выключении» стоячей волны фотон лежит прямо к другому анализатору с иной ориентацией.
Процесс переключения ориентации занимает около 10 нс. Генераторы, питающие оба переключателя, действуют независимо, хотя сам процесс имеет, скорее, периодический, чем случайный характер. Это обстоятельство, к сожалению, не позволяет с полной определенностью интерпретировать результаты эксперимента. Расстояние между анализаторами составляло 13м, так что сигнал с максимально возможной скоростью (равной, согласно специальной теории относительности, скорости света) распространится от одного анализатора до другого за 40 нс. Это означает, что выбор ориентации первого поляризационного анализатора не должен повлиять на прохождение фотоном второго анализатора, и наоборот. Таким образом, в эксперименте удовлетворяется условие локальности Белла. Следовательно, в соответствии с теоремой Белла должны были бы наблюдаться некоторые нарушения предсказаний квантовой механики относительно корреляций.
Однако все дело в том, что эксперимент привел к совсем иным результатам. Данные о корреляции в пределах экспериментальных ошибок согласуются с квантовомеханическими предсказаниями, сделанными на основе квантового состояния ψ0. Кроме того, полученные данные более чем на пять стандартных отклонений отличаются от предельных значений, допускаемых теоремой Белла для любой локальной модели со скрытыми параметрами.
Несмотря на то что эксперимент Аспекта и его коллег не дает вполне однозначного ответа, большинство ученых считают, что шансы на то, что будущие эксперименты опровергнут полученные результаты, чрезвычайно малы. Возможность спасения семейства локальных моделей со скрытыми параметрами представляется практически невероятной. Похоже, что странные свойства квантового мира — объективные неопределенность, случайность и вероятность, а также нелокальность — навсегда утвердились в физике.
Одно из самых странных свойств квантового мира — нелокальность. При некоторых обстоятельствах измерения, проводимые над одним из фотонов, по-видимому, мгновенно влияют на результаты измерений над другим фотоном. Можно ли использовать этот факт для передачи послания со скоростью, превышающей скорость света? К счастью, для специальной теории относительности ответ на этот вопрос отрицателен. Главное предположение этой теории, что никакой сигнал не может превысить скорости света, остается в силе.
МОЖНО кратко пояснить, почему так происходит. Представим себе двух людей, которые собираются обменяться сообщениями с помощью прибора, аналогичного устройству по проверке моделей со скрытыми параметрами. Пусть источник коррелированных пар фотонов находится между наблюдателями. У каждого из них имеется поляризационный анализатор и фотодетектор. Наблюдатели могут произвольным образом ориентировать оптические оси своих анализаторов.
Предположим, что оба наблюдателя договорились направить оптические оси вертикально. Тогда всякий раз, как будет испущена пара фотонов, должна наблюдаться сильная корреляция конечных результатов: либо оба фотона пройдут через анализаторы, либо оба фотона будут задержаны. Но пока наблюдатели изолированы друг от друга, эта сильная корреляция не проявится для каждого из них. Первый наблюдатель увидит, что половина фотонов в среднем проходит через анализатор, а половина — задерживается. Второй наблюдатель на своем анализаторе обнаружит такую же картину. Иными словами, каждый из изолированных наблюдателей обнаружит только случайную картину прохождения и задержки фотонов в анализаторах.
Теперь вообразим, что первый наблюдатель пытается закодировать некое послание своему коллеге, изменяя ориентацию своего анализатора. В зависимости от этой ориентации на каждом детекторе должна существовать сильная или частичная корреляция между событиями. Однако снова каждый из наблюдателей увидит, что в половине случаев фотоны проходят сквозь анализатор, а в половине случаев — задерживаются. Таким образом, независимо от взаимной ориентации анализаторов каждый из изолированных наблюдателей увидит статистически идентичные случайные распределения актов прохождения и поглощения фотонов. Квантовые корреляции между фотонами можно обнаружить, лишь сравнивая данные, полученные на каждом детекторе. Поэтому попытка использовать квантовые корреляции для передачи информации быстрее скорости света обречена на неудачу.
В этом смысле между квантовой механикой и специальной теорией относительности установилось мирное сосуществование, даже вопреки квантовомеханической нелокальности. Поэтому обманчиво и даже просто неверно утверждение, что квантовая механика возвращает нас к действию на расстоянии, которое было присуще дорелятивистским теориям, как, например, ньютоновской теории тяготения. Соблазнительно представить квантовомеханическую нелокальность как «страсть на расстоянии». Такой образ не претендует на объяснение странных корреляций, а лишь подчеркивает, что с их помощью нельзя передать никакого физического воздействия со скоростью, превышающей скорость света.
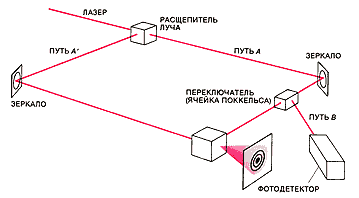
ДРУГОЙ эксперимент, называемый экспериментом с запаздывающим выбором, был предложен в 1978 г. Дж. Уилером, работавшим тогда в Принстонском университете. Он также демонстрирует странности квантового мира. Основной частью установки является интерферометр, в котором световой луч может быть расщеплен и вновь сложен. Лазерный импульс направляется на расщепитель луча, который ориентирован так, чтобы половина луча проходила через него, а другая половина отражалась под прямым углом к направлению распространения исходного импульса. Если затем световые лучи, прошедшие разными путями, вновь соединяются, то возникает интерференционная картина, доказывающая волновую природу света.
Предположим теперь, что интенсивность лазерного излучения уменьшена настолько, что в любой момент времени в интерферометр попадает только один фотон. В этом случае можно задать два различных вопроса. Летит ли фотон по одному из двух путей, так что он либо проходит через расщепитель, либо отклоняется им, т. е. проявляет свойства частицы? Или фотон в некотором смысле одновременно и проходит, и отклоняется, так что интерферирует сам с собой, проявляя тем самым свойства волны?
Ответ недавно был дан К. Аллеем, О. Якубовичем и У. Виксом из Университета шт. Мэриленд в Колледж-Парке и независимо Т. Хельмутом, Г. Вальтером и А. Зайонцем из Мюнхенского университета. Обе группы нашли, что фотон ведет себя как частица, когда измеряются частицеподобные свойства, и как волна, когда измеряются волновые свойства. Замечательным новшеством, внесенным этим экспериментом, является то, что решение измерять частицеподобные или волновые свойства принимается после взаимодействия каждого фотона с расщепителем луча. Следовательно, в самый критический момент взаимодействия с расщепителем фотон еще не «проинформирован», как ему следует себя вести (как частице или как волне), т. е. выбрать один из двух возможных путей или распространяться по обоим сразу.
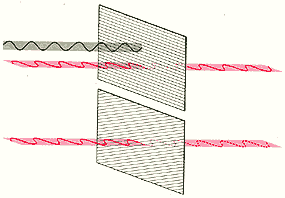
Длина обоих путей составляет около 4,3 м, так что фотон преодолевает это расстояние за 14,5 нс. Ясно, что обычные механические устройства не могут за столь короткое время переключиться с измерения частицеподобных свойств на измерение волновых. Однако такую «ловкость» может проявить так называемая ячейка Поккельса, которая срабатывает за время, меньшее 9 нс. Ячейка Поккельса содержит кристалл, который во внешнем электрическом поле способен расщепить световой луч на две части. Так происходит из-за того, что свет, поляризованный вдоль одной из осей кристалла, распространяется с иной скоростью, чем свет, поляризованный в перпендикулярном направлении. Подобрав должным образом электрическое поле и геометрию прибора, можно добиться того, что поляризованный свет, попадающий в ячейку, выходит поляризованным в перпендикулярном направлении. Ячейка Поккельса устанавливается на одном из возможных путей, по которым летит фотон после взаимодействия с расщепителем луча в интерферометре (см. рисунок вверху).
ПОЛЯРИЗИРУЮЩАЯ пленка является вторым основным элементом, необходимым для переключения с измерения частицеподобных свойств фотона на измерение его волновых свойств. Свет, выходящий из ячейки Поккельса, попадает на пленку. Если ячейка «включена», то свет поляризуется таким образом, что отражается пленкой в фотодетектор. В этом случае мы получаем ответ на вопрос, по какому пути прошел фотон, т. е. измеряем его частицеподобные свойства. Если же ячейка «выключена», то поляризация выходящего из нее света такова, что он проходит сквозь пленку и складывается затем со светом, прошедшим по другому пути. В этом случае интерференционные эффекты подтверждают волновую природу фотона.
Обе группы исследователей сообщили о результатах, которые прекрасно согласуются с квантовой механикой. Их работы доказали, что выбор между двумя возможностями действительно можно сделать и после взаимодействия фотона с расщепителем луча в интерферометре.
Как интерпретируются результаты, полученные в экспериментах с запаздывающим выбором? Прежде всего стоит отмежеваться от выдвигаемой иногда экстравагантной интерпретации, согласно которой квантовая механика допускает в некотором смысле «путешествия в прошлое». Квантовая механика не может сделать так, чтобы в прошлом произошло нечто, чего там не происходило. В частности, квантовая механика не может заставить фотон выбрать в нулевой момент времени один из двух возможных для него путей, если спустя 12 не включается ячейка Поккельса. Она не может заставить фотон выбрать сразу оба пути, если после того ка'к выбор сделан, ячейка выключается.
Более естественной представляется интерпретация, согласно которой объективное состояние фотона в интерферометре оставляет многие его свойства неопределенными. Если квантовое состояние полностью учитывает все свойства фотона, то такой вывод не вызывает удивления: в любом квантовом состоянии некоторые свойства остаются неопределенными. Но такое заключение приводит к следующему вопросу: как и когда неопределенные свойства становятся определенными? Ответ Уилера гласит, что «ни одно элементарное квантовое явление не существует как явление, пока оно не наблюдается». Другими словами, переход от неопределенности к определенности не завершен до тех пор, пока не произошел «необратимый акт увеличения», например почернение зерен фотоэмульсии. Однако исследователи основ квантовой механики не согласны с ответом Уилера. Следующий эксперимент показывает, почему вопрос все еще остается открытым.
В 1935 г. Э. Шредингер предложил знаменитый мысленный эксперимент. Пусть фотон падает на полуотражающую посеребренную пластинку, так что вероятности его прохождения и отражения равны 1/2. Если фотон проходит через зеркало, он запускает устройство, которое разбивает бутылку с цианистым калием и тем самым убивает кошку, сидящую в закрытой коробке. Пока коробка не будет открыта, невозможно определить, жива кошка или убита.
В таком положении дел не было бы ничего удивительного, если бы прохождение фотона через зеркало имело объективный характер, но оставалось совершенно неизвестным наблюдателю. Однако прохождение фотона принципиально неопределенно. Тогда столь же неопределенно событие с разрушением бутылки и в конечном итоге вопрос о жизни или смерти кошки. Другими словами, кошка находится между жизнью и смертью до тех пор, пока не будет подвергнута прямому наблюдению. Вывод парадоксален, но по крайней мере он касается только мысленного эксперимента.
В наше время уже труднее отвергнуть этот парадокс, поскольку нечто подобное мысленному эксперименту Шредингера было воплощено на практике несколькими группами ученых. Этим занимались Р. Восс и Р. Вебб из Исследовательского центра им. Уотсона фирмы IBM в Йорктаун-Хайтс, Л. Джакель из AT&T Bell Laboratories, M. Деворе из Беркли и Д. Шварц из Университета шт. Нью-Йорк в Стоуни-Брук. В определенной степени их работа основывалась на вычислениях, выполненных А. Леггетом из Иллинойского университета в Эрбана-Шампейн и С. Чакраварти из Стоуни-Брук и другими учеными.
Установка состоит из сверхпроводящего кольца, разомкнутого тонким слоем изолятора (так называемый джозефсоновский контакт). Однако электрический ток может циркулировать по такому кольцу благодаря «туннелированию» электронов через изолятор. Этот ток порождает магнитное поле.
В данной системе интерес представляет магнитный поток через кольцо, который (если поле однородно) равен произведению площади кольца на компоненту магнитного поля вдоль направления, перпендикулярного плоскости кольца. Если бы кольцо не было разомкнуто, то магнитный поток находился бы внутри кольца в «ловушке». Изолятор позволяет магнитному потоку «соскользнуть» с одного значения на другое. С помощью современных магнитометров величину магнитного потока можно измерить с фантастической точностью. Магнитный поток следует рассматривать как макроскопическую величину, поскольку он создается движением огромного числа (около 1023) электронов. Полученные результаты позволяют утверждать, что можно получить такие состояния сверхпроводящего кольца, в которых магнитный поток не имеет определенного значения. Это и есть проявление квантово-механических закономерностей, ранее наблюдавшихся только в микроскопических системах.
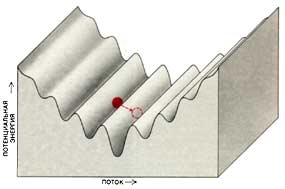
Чтобы понять, каким образом в этом эксперименте устанавливается квантовая неопределенность, необходимо учесть, что при каждом значении потока кольцо обладает некоторой потенциальной энергией. Казалось бы, поток через кольцо не может самопроизвольно измениться, так как потенциальный барьер отделяет два соседних значения потока друг от друга. Согласно классической физике, переходы между двумя значениями потока запрещены, если какой-нибудь внешний источник энергии, как правило тепловой, не помогает перейти через потенциальный барьер. Однако с точки зрения квантовой механики можно без всякого внешнего источника энергии «просочиться» сквозь барьер (туннельный эффект). Упомянутые выше группы экспериментаторов показали, что поток действительно меняется от одного значения к другому и что это изменение не может полностью происходить за счет тепловой энергии. Наблюдаемое туннелирование по крайней мере частично должно быть квантовомеханическим, особенно при очень низких температурах. Но квантовомеханическое туннелирование приводит к принципиальной неопределенности потока, который из-за этого не может быть локализован точно или близко к тому или иному значению.
Экспериментальная демонстрация квантовой неопределенности макроскопической переменной самим фактом своего существования не противоречит цитировавшемуся выше утверждению Уилера. Отсюда, однако, следует, что «увеличение», т. е. переход с микроскопического на макроскопический уровень, еще не избавляет от квантовомеханической неопределенности. Ударение в утверждении Уилера относительно «необратимого акта увеличения» следует поставить на слове «необратимый». Вопрос об условиях, при которых происходит такой необратимый процесс, еще далек от разрешения в современной теоретической физике. Некоторые исследователи (включая меня) считают, что нужны новые физические принципы, чтобы понять особенности той необратимости, которая возникает, когда в процессе измерения неопределенная наблюдаемая становится определенной.
ИССЛЕДОВАНИЯ «странностей» квантового мира продолжаются. Недавно выполнены и другие эксперименты, некоторые из них еще не завершены. Здесь следует упомянуть эксперименты двух типов, хотя у нас нет возможности обсудить их детально. В экспериментах с нейтронными интерферометрами, проведенных Г. Раухом и А. Зайлингером из Атомного института австрийских университетов, С. Вернером из Университета шт. Миссури в Колумбии и К. Шуллом из Массачусетского технологического института и их сотрудниками, волновая функция нейтрона расщепляется кристаллической пластинкой и затем соединяется одной или несколькими другими пластинками. При рекомбинации возникают интерференционные эффекты, которые демонстрируют ряд замечательных свойств, включая неопределенность пути нейтрона через интерферометр. Наконец, Р. Чамберс из Бристольского университета, Г. Мюлленштедт из Университета в Тюбингене и А. Тономура из Hitachi, Ltd. подтвердили с помощью электронных интерферометров знаменитый эффект Ааронова—Бома. Эффект заключается в том, что электрон «чувствует» присутствие магнитного поля в некоторой области, хотя вероятность обнаружения электрона в этой области равна нулю. Это впечатляющая демонстрация некоторого вида нелокальности, отличной от нелокальности, проявляемой при корреляциях пары фотонов, хотя и как-то с ней связанной. Полное понимание связи между нелокальностью двух видов, равно как и многих других озадачивающих результатов, полученных в экспериментах по изучению природы квантового мира, требует дальнейшей работы.
Абнер Шимони Реальность квантового мира // «Академия Тринитаризма», М.,Эл № 77-6567, публ.10950, 21.01.2004
[Обсуждение на форуме «Институт Физики Вакуума»]
Реальность квантового мира
Эйнштейн считал, что квантовая механика дает неполное описание физических систем. Лабораторные эксперименты показывают, что он, по-видимому, ошибался и мы должны смириться со «странностями» квантового мира

|
| Рис.1 |
|
| Рис.2 |
|
| Рис.3 |
|
| Рис.4 |
|
| Рис.5 |
|
| Рис.6 |
|
| Рис.7 |
 |
| Рис.8 |
В Мире науки, №3, 1988, стр.22
Абнер Шимони Реальность квантового мира // «Академия Тринитаризма», М.,
|
|