|
|
|
Г.И. Шипов
Содержание
-
Введение
- 1 Однотактный инерцоид Толчина
- 2 Экспериментальный график движения центра масс
- 3 Силы, действующие на центр масс инерцоида
- 3.2 Демонстрация нарушения третьего механики Ньютона
- 3.2.2 Инерцоид на качелях
- 3.2.3 Инерцоид на подвесе
- 4.2 Мощные инерциоиды
- 4.3 Инерциоид, управляемый компьютером и движущийся только вперед
- 5.2 Инерциоид под действием внешних сил
- 7 Основы механики Декарта
- 7.2 Преобразования Галилея и неголономные угловые координаты
- 7.3 Задание трансляционной скорости через псевдоевклидовы углы
- 7.4 Инерцоид Толчина как четырехмерный гироскоп
- 7.5 Трехмерная ориентируемая точка и вращательная метрика
- 8.2 Связь торсионных полей с полями инерции
- 8.3 Уравнения, описывающие динамику торсионных полей
- 8.4 Теория гравитации в механике Декарта
- 8.4.2 Локально инерциальные системы отсчета первого и второго рода в механике Декарта
- 9.2 Эксперименты, подтверждающие пространственно-временную прецессию свободного 4D гироскопа
- 12 Экспериментальное подтверждение явления механической индукции
- 12.2 Короткий удар, демонстрирующий переход вращательной энергии в энергию центра масс
- 12.3 Многократный короткий удар 4D гироскопа
- 15 Некоторые модели 4D гироскопов, демонстрирующие явление самоиндукции
- 15.2 Модель № 2 с электрическим приводом
- 15.3 Модель № 3 с управлением движением через компьютер
- 16.2 Реактивное движение без отбрасывания массы
- 16.3 Эксперименты Н.В. Филатова, подтверждающие возможность реактивного движения без отбрасывания массы
-
3.1 Исключение действия аэродинамических эффектов и обеспечение движения только вперед без остановки
-
3.2.1 Инерцоид на тележке индикаторе
-
4.1 Демонстрация нарушения закона сохранения момента
-
4.3.1 Компьютерное управление изменением направления тяги
-
5.1 Свободный инерциоид
-
7.1 Вращение и силы инерции
-
8.1 Уравнения движения четырехмерной ориентируемой точки
-
8.4.1 Соответствие с теорией гравитации Эйнштейна
-
9.1 Пространственно-временная прецессия свободного 4D гироскопа
-
10.1 Геометризация внешних сил
-
12.1 Короткий удар, демонстрирующий переход поступательной энергии центра масс во вращательную энергию
-
13.1 Явление механической самоиндукции в механике Декарта
-
15.1 Модель № 1 с пружинным заводом
-
16.1 Инерционная масса как мера поля инерции
-
17.1 Локальное кручение и кривизна пространства, создаваемая угловым ускорением N
Введение
В 1977 году вышла замечательная книга гениального Российского инженера Владимира Николаевича Толчина под названием «Инерцоид, силы инерции как источник движения» [1]. Уже само название книги вызвало бурю эмоций у научной общественности, особенно в стане противников работ В.Н.Толчина. Дело в том, что при теоретических рассуждениях силы инерции рассматриваются некоторыми учеными как «псевдоактивные силы», имеющие математическое происхождение [2].
Другая часть ученых считает силы инерции вполне реальными силами, способными изменять энергию системы в ускоренных системах отсчета [3]. Эти силы обладают оригинальным свойством - они не удовлетворяют третьему закону механики Ньютона, поскольку неизвестно со стороны каких тел они приложены [3].
Реальность сил инерции не подвергали сомнению такие известные механики как О.Хвольсон, Р.Поль, А.Вебстер, а среди физиков Нобелевские лауреаты М.Планк и А. Эйнштейн. Действительно, сильный принцип эквивалентности, которым руководствовался А.Эйнштейн при построении релятивистской теории гравитации, устанавливает эквивалентность не только однородных гравитационных полей c однородными полям инерции, но и эквивалентность сил, порожденных этими полями. М.Планк указывает на принцип Даламбера, когда силы инерции уравновешивают другие вполне реальные силы. Состояние невесомости, которое мы наблюдаем внутри космического корабля на стационарной орбите, было бы невозможным, если бы сила гравитации не была скомпенсирована силой инерции.
Оказывается, что вопрос о правильном понимании сил инерции вызывает не только академический интерес, но и имеет далеко идущие практические следствия. Пренебрежительное отношение к реальному проявлению сил инерции зачастую ведет к поломкам механизмов. Как отмечает Л.Б.Левенсон [4]: «С увеличением мощности и быстроходности участились поломки машин. Стало особенно заметно давнее разногласие по существенному вопросу о силах инерции: на первых двух курсах студентов учили в теоретической механике, что силы инерции вовсе не существуют, что они лишь воображаемые и вводятся в расчет для удобства его, отнюдь не будучи реальными, что силы инерции условный геометрический вектор, математическая фикция и т.д. А через год в курсе тепловых двигателей их заставляли складывать действительные давления пара на поршень с несуществующей силой инерции движущихся частей, чтобы получить истинную результирующую силу. Всякое пренебрежение, всякий недоучет этой «вовсе не существующей»силы неизбежно влечет за собой поломки, крушения и тому подобные реальные последствия».
Итак, если силы инерции реальны, то вполне правомерно поставить вопрос об использовании этих сил (в механике известно четыре типа сил инерции [3]) для передвижения механических систем, что и делает В.И.Толчин.
Особо отметим, что силы инерции не удовлетворяют третьему закону механики Ньютона [3], поэтому на них не распространяются теоремы, которые доказаны с применением третьего закона -закона действия и противодействия. Например, теорема о сохранении импульса центра масс изолированной механической системы, которая доказывается при условии, что внутренние силы системы удовлетворяют третьему закону механики Ньютона. Более того, силы инерции невозможно отнести не к внутренним и не к внешним силам по отношению к некоторой механической системе. В связи с этим М.Планк разделяет силы, действующие на систему, на внутренние, внешние и силы инерции [5].
Мы не будем вступать в противоречие с логикой, если допустим возможность изменять импульс центра масс, изолированной от внешних сил системы, под действием сил инерции, искусственно созданных внутри самой системы. Именно это, в конечном счета, доказывают многочисленные эксперименты В.Н.Толчина, проведенные им с инерцоидами различного типа [1].
Совершенно очевидно, что теоретическое описание этого явления выходит за рамки механики Ньютона и требует использование новой механики, названной автором механикой Декарта. Первоначальный вариант механики Декарта опубликован в работе [6], а ее окончательные принципы и уравнения доложены в 2005 г. на Международной конференции, посвященной столетию специальной теории относительности [7].
Механика Декарта представляет собой четвертое обобщение механики Ньютона: первое обобщение -релятивистская механика ЭйнштейнаЛоренцаПуанкаре (1905 г.), второе -общерелятивистская механика Эйнштейна (1915 г.), третье -квантовая механика БораШредингера (1926 г.). Принципиальные отличия механики Декарта от всех предыдущих это:
- 1) отсутствие понятия инерциальной системы отсчета;
- 2) замена материальной точки ориентируемой материальной точкой;
- 3) геометризация механики;
- 4) относительность всех видов полей и взаимодействий -
Всеобщая относительность [8].
В настоящей работе будет показано, что разумное, согласующееся с экспериментальными данными, объяснение движения инерциоида Толчина возможно только в рамках механики Декарта, а не механики Ньютона. В научной литературе существуют теоретические работы, которые базируются на гипотезе движения инерцоида за счет сил трения [2], [9], однако детальное исследование этих работ показывает, что авторы либо описывают устройство, не совпадающее с конструкцией инрецоида (см.[2]), либо неправильно составляют уравнения движения (см.[9]). Кроме того, создается впечатление, что авторы указанных теоретических работ не знакомы с экспериментами В.И.Толчина или полностью игнорируют их. Всякий понимает, что одно дело теоретическая модель движения инерцоида, предполагающая его движение за счет сил трения [9], и совсем другое экспериментальные данные, полученные на прецизионной установке [10]. Несомненно, силы трения вносят определенный вклад в движение инерцоида, но не объясняют наблюдаемое движение во всех деталях [10].
1 Однотактный инерцоид Толчина
Когда смотришь на однотактный инерцоид Толчина, представленный на рис. 1 и 2, всегда удивляешься простоте и гениальности его устройства.

Рис. 1: Однотактный инерцоид Толчина с пружинным заводом
На металлической платформе 1 с тремя свободно вращающимися колесами 2, установлена пружина 6, которая служит источником внутренней энергии. Запасенная пружиной энергия через систему шестеренок 7 передается на два груза 5, вращающихся синхронно в противоположные стороны.
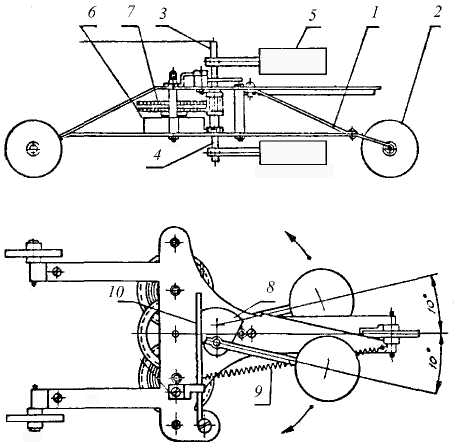
Рис. 2: Схематическое изображение однотактного инерцоида
Во время вращения кулачок 8, жестко закрепленный на оси вращения 3, набегает на планку 10, к которой прикреплена пружина 9. Кулачок 8 и пружина 9 в совокупности представляют собой мотортормоз. Назначение мотортормоза состоит в том, чтобы ускорять вращение грузов в секторе углов 330º − 360º и замедлять в секторе углов 150º − 180º. Этот существенный элемент инерцоида всегда опускался из рассмотрения оппонентами Толчина, поэтому уравнения движения инерцоида, исследованные, например, в статье Е.Л. Тарунина и др. [9] просто неверны.
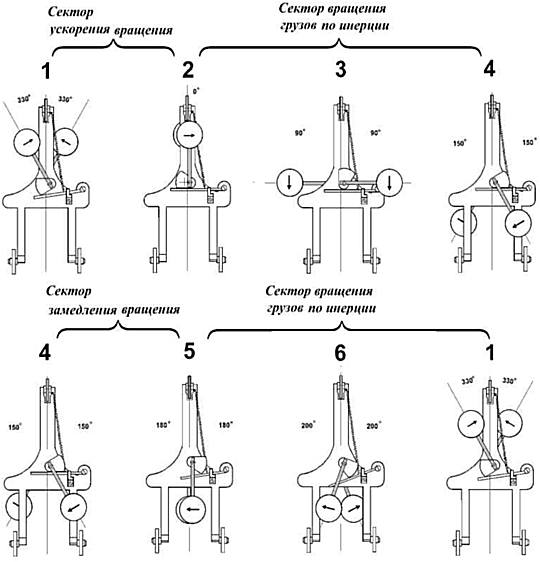
На рис. 3 представлены поэтапные действия мотортормоза за один такт инерцоида. В действительности же на вращение грузов оказывает влияние как пружина 9, так и пружина 6. Разница в их действии состоит в том, что пружина 6 создает момент L6, который почти на два порядка меньше момента L9, создаваемого пружиной 9. Эксперимент показывает, что если убрать пружину 9, то энергии пружины 6 хватает только на поддержание вращения грузов 5, при этом инерцоид превращается в симметричный вибратор, центр масс которого покоится или движется с постоянной скоростью.
|
| |
Рис. 3: Действие мотортормоза приводит к изменению частоты вращения грузов 5. В секторе улов 330º − 360º угловая скорость увеличивается, а в секторе углов 150º − 180º уменьшается
Полный текст можно посмотреть в:
- формате PDF (1025Кб)
 - файл экранного качества (для просмотра);
- файл экранного качества (для просмотра); - формате PDF (10240Кб)
 - файл высокого качества (для печати);
- файл высокого качества (для печати);
Г.И. Шипов, 4D гироскоп в механике Декарта // «Академия Тринитаризма», М.,
|
|