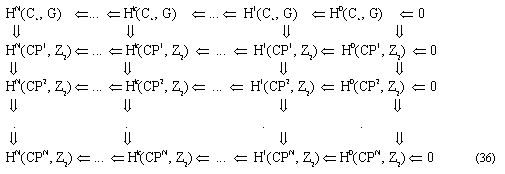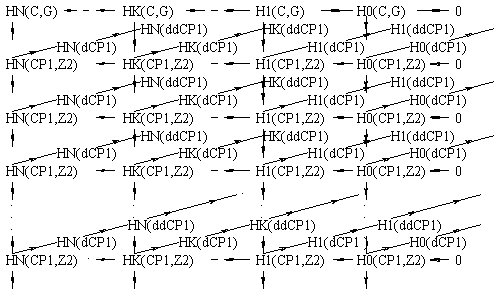|
|
|
Смелов М.В.
Электромагнитные солитоны вакуума. Часть 2. «Топологические характеристики электромагнитных солитонов»
Введение
В современных теориях единого поля структура пространства-времени вакуума физических полей вводится априорно, полагаясь на принцип релятивистской инвариантности, вытекающий из ошибочных «основополагающих» экспериментальных опытов Майкельсона-Морли, доказывающих инвариантность скорости света С. Поэтому в специальной теории относительности (СТО) этот факт просто постулируется. Известно [1], что все подобные эксперименты с противонаправленными электромагнитными лучами не могут дать истинной информации о процессе распространения фотона в силу лоренцевых изменений экспериментальных масштабов квадратично по нормированной скорости (+V)2/C2 . Хуже того в 4-х мерных уравнениях электродинамики (и квантовой релятивистской также) величина C2 – есть априорный скаляр (возможно модуль скорости света), но не скорость как вектор, зависящий от 4-х проекций: C = (C0, C1, C2, C3), а потому не известно куда он направлен согласно этим уравнениям. Кроме того в соответствии с гипотезой фотонов-частиц (в скрытой форме уже содержащейся в СТО), масса которых много меньше массы измерительных зеркал или дифракционных решёток, эксперименты на отражение и преломление таких лёгких частиц (без отдачи) всегда покажут постоянство их скорости относительно любых движущихся систем отсчёта-зеркал, автоматически согласуясь с СТО. Поэтому все теоретические и экспериментальные исследования выше упомянутых полей не позволят в принципе доказать или опровергнуть априорный релятивизм логически, то есть определить (измерить) природу электромагнитных и других полей, в проекции на саму электродинамику или её многочисленные обобщения, находясь в системе аксиом этих теорий, базирующихся на постулате. Например в [1] рассмотрены эксперименты с однонаправленными световыми лучами, которые должны были бы измерить эффекты пропорциональные V/С в рамках той же электродинамики, но не обнаружившие таких эффектов по указанным выше тем же причинам.
Чтобы хоть что-нибудь понять в механизме движения фотона, а следовательно и природу других частиц, необходимо выйти из 4-х мерного пространства-времени (и его электродинамики) и взглянуть как бы со стороны теоретически и экспериментально на это пространство-время.
В данной работе предпринята такая попытка путём поднятия или не тривиального продолжения нелинейно связанной системы уравнений электромагнитного поля Максвелла и фермионных уравнений Дирака в расслоенное гиперкомплексное (мультигексанионное) проективное пространство ~1022 –измерений, топология которого описывается фрактальной геометрией вложенных гиперповерхностей. Причём эта размерность вычисляется в самой теории внутренним образом, а не задаётся априорно.
Вычисленная группа симметрии этих уравнений включает в себя все известные группы симметрий полей, элементарных частиц, атомов, молекул, она описывает их как солитоны этого расслоенного пространства фрактальной геометрии, но в проекции на наблюдаемое 4-х мерное пространство-время.
В работе приведены результаты расчёта скорости света и всех известных констант взаимодействий: гравитационных, электромагнитных, сильных и слабых, а так же дано соотношение их взаимосвязи, с любой наперёд заданной точностью непертурбативным методом алгебраической (комбинаторной) топологии. То есть фактически строится солитонодинамика известных и новых природных сущностей.
В солитонодинамике нет действия полей (причинно-следственного), но существует только их взаимообусловленность (корреляция) в частности нелинейная интерференция солитонов передатчика и приёмника. Именно эти технические устройства [11], базирующиеся на указанной топологии, были созданы и испытаны на предмет их функционирования и исследования процессов распространения электромагнитных солитонов (ЭМ-солитонов), частным случаем которых являются фотоны, нейтрино, гравитоны, электроны, протоны, атомы и молекулы (в частности биомолекулы и биосистемы). В основе принципа деятельности таких измерительных устройств лежит свойства когерентных спиновых систем (ферримагнетиков) обнаруживать движения (метаморфозы) субстанций пропорциональные именно V/C, а не V2/C2, так как спиновые объекты в соответствии с релятивистским уравнением Паули учитывают релятивистские эффекты взаимодействия пропорциональные V/C. Кроме того в приёмнике используется неэлектродинамическое взаимодействие солитонов, в виде корреляции инстантонов передатчика и приёмника, где инстантонами или топологическими солитонами являются нулевые моды или фликкер-шум магнитных солитонов ферримагнитных антенн приёмопередатчиков.
Некоторые топологические характеристики ЭМ-солитонов.
В данной работе описываются результаты топологического исследования солитонного уравнения, которые определяют электромагнитные солитоны вакуума внутренним образом. В работе [2] теоретически обнаружено, что солитонное решение j 0, определённое на подгруппе всей группы G симметрии поля j m(xn) солитонного уравнения, выделяется тем, что группа G становится группой автоморфизмов (т.е. Gj 0 = j 0) более того эта группа является группой автоморфизмов симметрии координатного пространства {xn} этих солитонов (Gx = x). Показано так же, что солитонные функции поля j (x) как преобразования этих координат определяют инвариантную подгруппу всей группы G (т.е. G –1 j G = j). Тогда согласно [3] группа симметрии этих уравнений состоит из диффеоморфизмов пространства джетов (струй), не меняющих самого уравнения и переводящее каждое решение этого уравнения в некоторое другое решение того же гомотопического индекса или топологического сектора вакуума. Причём в башне джетов cогласно [3] координатами 0-джета является m+n =M- мерное пространство XM обобщённых координат {xn, j m} лагранжиана. При этом независимые переменные xn определяют многообразие базы (4-х мерное пространство-время) всего расслоенного пространства Jk(n,m) (J-джетов) в виде дифференциальных продолжений (или фрактализаций в случае конечных разностей см. ниже) по Ли-Овсянникову исходного солитонного уравнения, приведённого к виду системы нелинейных дифференциальных уравнений в частных производных первого порядка :
J1(n,m) = F(XM, PK} = {f i ((xn, j m), d j m/dxn)}=0, где PK — обобщённые скорости (импульсы для гамильтониана). Это уравнение, являясь 1-джетом, определяет гиперповерхность коразмерности i или график 1-джета в пространстве (в многообразии) RA размерности
A = M+K = (n + m) + (n ґ m). Пространство XM рассматривается как новая (вложенная) база в иерархии башни джетов. Действие имеет вид s = т L(XM (t), dXM/ dt) dt, где L — лагранжиан.
Известно [3], что факторобъетом такого инвариантного действия является пространство орбит фазового пространства гамильтоновой динамической системы. Это пространство орбит, являясь факторпространством, имеет симметрию факторгруппы (факторалгебры) группы G по инвариантной подгруппе j m. Тогда в данном факторпространстве существует факторуравнение, получаемое факторизацией исходного уравнения поля, например в виде дифференциальной системы первых форм Картана-Пфаффа, задающих распределение Картана (касательные плоскости) на гиперповерхности, определяемой видом исходных уравнений поля в форме уравнений Эйлера-Лагранжа (ЭЙЛАГ). Уравнения ЭЙЛАГ есть вариационная производная лагранжиана. Причём лагранжиан рассматривается в виде (M- 1)- мерной гиперповерхности индикатрисы [5], вложенной аналогично 1-джету в расслоенное пространство XM-1(XM) — центрально-аффинного пространства E2M -1. Причём двойственная к ней гиперповерхность (в обобщённых координатах импульс-поле), называемая фигуратрисой, является гиперповерхностью гамильтониана с уравнением движения на ней в форме уравнений Гамильтона-Якоби (ГАМЯК). Система уравнений Дирака-Максвелла в [2] для инстантонов (как солитонов с мнимым, повёрнутым на 900, временем) имеет один и тот же вид как в форме ЭЙЛАГ, так и форме ГАМЯК, что является очевидным следствием факторизованной формы этих уравнений, записанных в расслоенном факторпространстве в виде комплексно проективного псевдоевклидова (спинорного) пространства, подпространством которого является пространство-время Минковского. Описанный признак солитонных уравнений: инвариантность их относительно преобразований Лежандра (перехода от формы уравнений ЭЙЛАГ к — ГАМЯК), обусловлен выше упомянутым автоморфизмом, который означает, что солитон, индуцированный в среде (вакууме), описываемой уравнениями приведёнными в [2], не отражается и не рассеивается этой средой, которую к тому же он в себе и вокруг себя создаёт. При этом в системе покоя ЭМ-солитона, когда среда двигается относительно него, этот солитон является безотражательным потенциалом некоторого уравнения Шрёдингера обратной задачи рассеяния [6], решением которой и является этот солитон. Причём согласно [6] введение коммутирующих операторов пары Лакса и преобразований Миуры-Гарднера [24] означает в конечном итоге переход от исходного уравнения движения в фазовом пространстве 2M-измерений к факторуравнению указанной обратной и прямой задачи рассеивания в некотором эффективном факторпространстве в виде проективного пространства RP M-1 (M-1 измерения), гладко вложенного в XM. Дифференциальные условия вложения RPM-1 в XM и есть солитонные уравнения, в частности при вложении гиперболического пространства RPM-1 (с гиперболической метрикой и антисимметричными коэффициентами второй основной формы гиперповерхности) в XM эти условия дают солитонное уравнение типа sin-Гордона, которые определяют инвариантность или постоянство функции распределения угла фазы (угла конуса гиперхарактеристик) между двумя гиперлучами (в виде направлений движения инвариантов Римана) двух противонаправленных волновых движений вакуума. С динамической точки зрения это постоянство фазы означает постоянную синхронизацию между двумя движениями в двух локальных областях гиперлиста Мёбиуса (для RPM-1 чётной размерности) и образование ЭМ-солитона как результата мнимоединичной интерференции (без гашения так как движение происходит на двух разных локальных гиперлистах) в виде спирально-винтового движения солитона, описываемого кватернионами. С геометрической точки зрения указанные характеристики как гиперлинии изофазы определяют локсодромическую сетку координат на гиперсфере RPM-1, вдоль которых тензоры переносятся абсолютно параллельно (в отличии от переноса Леви-Чевита в метрике Римана), то есть эта гиперсфера с крутильной деформацией материализует вычисленное в [2] пространство абсолютного параллелизма с кручением (АПК) ЭМ-солитона, именно это пространство АПК описывается уравнением вложения. Такое спирально-винтовое движение в расслоенном пространстве E2M -1 (собственным для ЭМ-солитона) в проекции на наблюдаемое 4-х мерное пространство порождает в среднегеометрическом от этих двух гиперболических движений, а именно конформного растяжения линейного интервала ds / (1 – v/c) на однополостном гиперболоиде (см. [11]) и конформного сжатия интервала ds / (1 + v/c) на лемнискатном торе Мёбиуса (связанных преобразованием инверсии радиуса), симметрию Лоренца-Пуанкаре полей -частиц в пространстве-времени Минковского, инвариант такого движения известен как среднегеометрический интервал этого пространства равный ds* = ds/(1 – v2/с2)1/2. Важно отметить, что выше упомянутое солитонное уравнение sin-Гордона очевидным образом трасформируется (для малых углов) в солитонное уравнение Клейна-Гордона с кубической нелинейностью, в уравнение НУШ или Гинзбурга-Ландау, а с помощью преобразования Хирото в уравнение Буссинеска и Лоренца-Друде поляризации нелинейной вакуумной цепочки.
Описанные результаты исследования можно рассматривать как частную задачу общей проблемы вложения (M – J) мерных гиперповерхностей-джетов (например лагражианов) в многомерное расслоенное многообразие E2M -1, решённую в основополагающей работе по фрактальной геометрии (фрактальной физике) [5]. В ней обобщается понятие метрики на эквиаральные (сохраняющие гиперплощадь) метрики типа Финслера. Кроме того обобщается понятие геометрических объектов смежных по размерности (J, J+1, J+2) : гиперлиния L, гиперповерхность S и гиперобъём V, которые являются гиперклетками триангуляции, указанных объектов как слоёв расслоенного многообразия. Что позволяет итерационно и наглядно сканировать этими объектами-слоями по всем размерностям слоёв расслоенного пространства, пренебрегая приближённо эффектом зацепленности слоёв, выражающейся в том, что для определение общих коммутационных соотношений (супералгебры) алгебр двух слоёв требуется введение дополнительного третьего слоя, — для супералгебры трёх слоёв требуется уже два дополнительных слоя, — для четырёх слоёв необходимо — три дополнительных слоя и т.д. Тем не менее для размерно-однородных топологиий [ 7 ], в которых i-мерная грань полиэдров триангуляции есть точное ребро приклеенного полиэдра размерности i +1, и с учётом инвариантности численного значения мер m, указанных объектов: m (L) = m (S) = m (V) = const (для всех размерностей слоёв), существует обобщённое понятие линейной гиперсвязности (в форме физического калибровочного поля) согласованной с эквиариальной гиперметрикой, а так же существует понятие параллельного переноса тензоров вдоль гиперлиний, кроме того есть понятие тензора кривизны R гиперповерхности S Римана и тензора кривизны K кручения Картана (или деформации Картана) гиперобъёма V, вмещающего пространства. Справедливы теоремы Стокса и Остроградского-Гаусса, существует аппарат обобщённого дифференциирования и интегрирования. Кроме этого определены аналоги деривационных уравнений Френе движения ориентирующего гипертрёхгранника Дарбу (гиперрепера-тетрады x) в проекции на его собственные гипероси, а следовательно и условия интегрирования этих деривационных уравнений в виде системы уравнений Гаусса-Патерсона-Кодацци [23] вложения гиперповерхности S в пространство V:
R = прS K)+ 2('bb L 'ba) Ы R l c , b a = Kik, pj x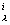 x
x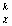 x
x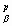 x
x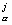 + (bl b bc a - bc b bl a), (1)
+ (bl b bc a - bc b bl a), (1)
пр^ S(K) = С L L ba Ы - Kik, pj x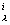 x
x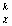 n px
n px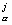 =
= 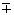 (С l bc b - С c bl b), (2)
(С l bc b - С c bl b), (2)
где верхний знак (+) соответстует единичной, а нижний — мнимоединичной гипернормали n p (гиперболической метрики) к гиперповерхности S, а знак L обозначает внешнии формы;
'bb = bl b — коэффициенты второй основной формы этой гиперповерхности, ассоциируемые с тензором упругих напряжений объёма вакуума как упругой среды,
С L — оператор производной Ли равный ковариантной производной С l в римановой связности на гиперповерхности S.
Тензор кривизны кручения в (1) Kik, pj, индуцирует в гиперповерхности S внешнюю кривизну кручения в виде проекции прS (K) = Kik, pj x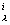 x
x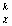 x
x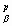 x
x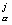 , соответствующую тензору Q l c b a в работе [2]. Система уравнений (1, 2) эквивалентна системе солитонных уравнений в [2], если в (1) провести свёртку по индексам a, c, а затем перейти к тензорам кривизны Риччи R l b = R l c , b c, тогда для гиперболических (волновых) движений в гиперплоскости S с гиперболической метрикой коэффициенты bl b антисимметричны (bb b = 0) и внешняя 2-форма bl b bc c - bc b bl c = bc b bl c. След этой формы имеет вид sp(bc b bl c) = bc a bc a / 4 для 4-х смежных гиперразмерностей слоёв, аналогично 4-х мерному пространству-времени. Тогда бесследовые тензоры внутренней и внешней кривизны (аналоги тензора кривизны Эйнштейна) равны соответственно R l b — gl b R/2 и Kik, pj x
, соответствующую тензору Q l c b a в работе [2]. Система уравнений (1, 2) эквивалентна системе солитонных уравнений в [2], если в (1) провести свёртку по индексам a, c, а затем перейти к тензорам кривизны Риччи R l b = R l c , b c, тогда для гиперболических (волновых) движений в гиперплоскости S с гиперболической метрикой коэффициенты bl b антисимметричны (bb b = 0) и внешняя 2-форма bl b bc c - bc b bl c = bc b bl c. След этой формы имеет вид sp(bc b bl c) = bc a bc a / 4 для 4-х смежных гиперразмерностей слоёв, аналогично 4-х мерному пространству-времени. Тогда бесследовые тензоры внутренней и внешней кривизны (аналоги тензора кривизны Эйнштейна) равны соответственно R l b — gl b R/2 и Kik, pj x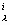 x
x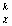 x
x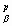 x
x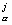 - sp (Kik, pj x
- sp (Kik, pj x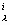 x
x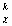 x
x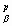 x
x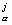 ), а уравнение (1) принимает вид подобный уравнению Эйнштейна, но для полной кривизны гиперпространства с правой частью:
), а уравнение (1) принимает вид подобный уравнению Эйнштейна, но для полной кривизны гиперпространства с правой частью:
(Rlb — gl bR/2) — (Kik, pj x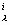 x
x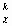 x
x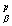 x
x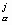 — sp (Kik, pjx
— sp (Kik, pjx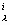 x
x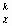 x
x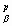 x
x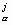 )) =
)) =
= — bc b bl c + gb l bc a bc a/4, (3)
где тензор мультипольной деформации (сжатия, изгиба и крутильного сдвига) гиперповерхности вакуума (как упругой оболочки) в левой части равен в правой части (по дифференциальному закону Гука) тензору натяжений этой упругой среды-вакуума в виде тензора натяжения Максвелла или тензора энергии-импульса электромагнитного поля, причём роль модуля упругости играет обратная гравитационной постоянной Эйштейна-Ньютона 8p G / c4. То есть — bc b bl c + gb l bc a bc a / 4 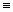 (8p G / c4) Ч (- Fc b Fl c + gb l Fc a Fc a / 4), и тогда гипертензор напряжённости поля Максвелла Fc b естественным образом равен тензору напряжений деформации bc b 8p G / c4 вакуума с тензором деформации гиперповерхности bc b. При этом во втором уравнении системы (1, 2) проекция кривизны вмещающего пространства на нормаль к гиперповерхности в простейшем случае представляется зональными, азимутальными и тессеральными гипершаровыми гармониками поля кривизны кручения гиперповерхности S в виде вложенных гиперсфер. Тогда эту проекцию можно сделать тождественно нулевой:
(8p G / c4) Ч (- Fc b Fl c + gb l Fc a Fc a / 4), и тогда гипертензор напряжённости поля Максвелла Fc b естественным образом равен тензору напряжений деформации bc b 8p G / c4 вакуума с тензором деформации гиперповерхности bc b. При этом во втором уравнении системы (1, 2) проекция кривизны вмещающего пространства на нормаль к гиперповерхности в простейшем случае представляется зональными, азимутальными и тессеральными гипершаровыми гармониками поля кривизны кручения гиперповерхности S в виде вложенных гиперсфер. Тогда эту проекцию можно сделать тождественно нулевой:
- Kik, pj x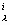 x
x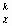 n px
n px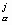
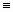 0 путём выбора специальных шарнирных условий сшивки этих сфер. Поэтому это уравнение при c = l становится известным тождеством для напряжённостей именно электромагнитного поля Максвелла (натяжения) вакуума:
0 путём выбора специальных шарнирных условий сшивки этих сфер. Поэтому это уравнение при c = l становится известным тождеством для напряжённостей именно электромагнитного поля Максвелла (натяжения) вакуума:
С l bl b - С l bl b = (8p G / c4) Ч (С l Fl b - С l Fl b) 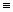 0. (4)
0. (4)
Совпадение геометрических условий вложения (1, 2) и динамических уравнений движения поля ЭМ-солитона в [2] или (3, 4) не случайное, а обусловлено тем, что уравнение движения поля солитона по геодезическим расслоенного пространства в форме ЭЙЛАГ или — ГАМЯК получено варьированием того же самого лагранжиана, который как гиперповерхность индикатрисы вкладывается в расслоеннное пространство большей размерности. Причём реперы-тетрады (они же волновые функции поля), образующие гипертрёхгранник Дарбу двигаются в том же самом расслоенном пространстве (по построению) по тем же самым геодезическим гиперорбитам солитона; этот сопровождающий трёхгранник естественным образом сцеплён с солитоном. Поэтому для поля ЭМ-солитона безразлично, варьировать ли динамическое действие поле или осуществлять вложение геометрии поля, окончательный результат изображений уравнения движения поля или вложения геометрии будет тождественным с точностью до обозначений. Поэтому поле солитона представляет собой совокупность геометрии в виде симметрии деформаций вакуума и напряжений этой деформации, а само солитонное решение определено на группе Ли этой симметрии как решение обыкновенных дифф. уравнений Пфаффа для распределения Картана касательного индикатрисе. Метод обратной задачи рассеяния [6] строит именно такое решение путём факторизации исходного уравнения поля с переходом в факторпространство (проективное пространство) вложимое в расслоенное многообразие большего числа измерений или фрактальное многообразие. При этом «голые» возбуждения вакуума в виде инстантонов или нулевых мод солитона «одеваются» классическим преобразованием Дарбу для потенциала:
V0 + Ln(det|A|), где A — матрицант в паре Лакса, вследствии действия ренорм-группы симметрии [9] в виде процесса фрактализации расслоенного пространства. Этот потенциал и есть ЭМ-солитонное решение, в котором калибровочная фаза Ln(det| A|) задаёт гипервращение поля вдоль векторов Киллинга в операторах группы Ли вокруг всего физического 4-мерного пространства (базы) на бесконечности. Такие же свойства солитонов следуют из общих принципов наименьшего действия в геометрической формулировке [8]. В соответствии с этой концепцией, вытекающей из упомянутой [5] теории вложенных гиперповерхностей, открыта система уравнений Вагнера-Жотикова (ВАГЖОТ) движения по геодезическим в расслоенном пространстве XM-1(XM) любого локально ориентированного линейного элемента-клетки (гиперполиэдра триангуляции), в котором определена (M-1)-мерная индикатриса, то есть внутренним образом. Эта система состоит из уравнения для тензора кривизны этого элемента и уравнение движения барицентра элемента-клетки. Причём уравнение в форме ВАГЖОТ имеет вид как уравнения ЭЙЛАГ касательного расслоения, базис которого определяет гомологию топологического пространства динамической системы, так и вид уравнения ГАМЯК кокасательного расслоения (базис которого определяет когомологию этой системы), то есть уравнение ВАГЖОТ инвариантно относительно преобразования Лежандра — из формы ЭЙЛАГ к — форме ГАМЯК, поэтому базис (функции поля) уравнения ВАГЖОТ автодуален, что означает согласно [10] инстантонный характер решений этого уравнения. Поскольку уравнениям ЭЙЛАГ волновых движений соответствует два характеристичеcких полуконуса, а уравнениям ГАМЯК — один полуконус, то уравнения ВАГЖОТ определяют склейку двух полуконусов ЭЙЛАГ в один полуконус ВАГЖОТ по изотропным гиперплоскостям (касающихся двух полуконусов) через бесконечность в гиперповерхность полнотория [10], изображающего в общем случае комплексное проективное пространство CPM-1 (для нечётного M-1 это полноторие становится неориентированным гипертором Мёбиуса). При этом инстантоны (функции склейки или нулевые моды ЭМ-солитона) двигаются в этих гиперплоскостях склейки. Процесс склейки, сохраняющий конформную симметрию уравнений относительно гиперсферы инверсии радиуса, ведёт к образованию букета торов Мёбиуса в виде замкнутых в нуле координат (лемнискатных) торов Мёбиуса и гиперболических торов Мёбиуса (для гиперболических движений поля) замкнутых на бесконечности (см. [11]). Образование проективного пространства RPM-1 или факторпространства означает, что уравнения ВАГЖОТ являются факторуравнениями движения поля и геометрии в этом факторпространстве. Это факторпространство в простейшем случае можно параметризовать преобразованием Лобачевского например в форме дробно-линейных преобразований гиперкомплексного проективного пространства CPM-1 введением гиперболической метрики для волновых движений полей. В общем случае эти преобразования определяют группу Мёбиуса (Mob), подгруппой которой является группа локсодромической симметрии [12], которая в свою очередь задаёт симметрию (геометрию) абсолютного параллелизма этого факторпространства. Как указывалось выше согласно [6] вложение факторпространства с гиперболической метрикой в виде псевдосферы проективного пространства в расслоенное гиперпространство осуществляется согласно солитонного факторуравнения sin-Гордона (f — Гордона в общем случае) путём решения обратной задачи рассеяния, но таким факторуравнением в рассматриваемом случае и является уравнение ВАГЖОТ, которое таким образом становится уравнением вложения или солитонным уравнением. Причём указанная выше система уравнений в [2] или (3, 4) имеет вид уравнений Янга-Миллса для тензорного потенциала, которые в гиперкватернионах : в гексанионах X(а,в), Y*(а,в), сводятся в солитонной калибровке к квазиодномерному уравнению Клейна-Гордона. Например ¶ 2X/¶ а ¶ в + X + X (Y*)2 = 0,
¶ 2Y*/¶ а¶ в + Y* + Y* X2 = 0 или ¶ 2Z/¶ а¶ в ± Z 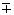 Z3 = 0 для дуальносопряжённого решения
Z3 = 0 для дуальносопряжённого решения
Y* = ± i X, где i — гексанионная мнимоединичная матрица (16 х 16). При этом верхний знак соответствуeт компоненте топологического солитона или инстантону (кинк-функции) в виде тензора кривизны Картана-Риччи кручения вакуума, определяющего сам факт существования топологического заряда (гомотопического сектора или индекса) вакуума как тензорную фазу единого солитонного поля, а нижний знак — компоненте динамического солитона (типа гиперболического секанса с собственным топ. зарядом равном 0) в виде тензора кривизны Римана-Эйнштейна квадрупольного сжатия-изгиба вакуума, но создаю-щего величину топологического заряд связанного ЭМ-солитона в виде гравитационно-инерционной массы Ньютона, электрического заряда Кулона и других фундаментальных констант. Результаты вычислений этих констант приведены в [11], а подробнее они будут опубликовано в следующей статье. Связанное состояние топологического и динамического солитона (пиннинг топ. солитона на неоднородности вакуума в виде дин. солитона) создаёт устойчивое образование в виде бризера в теории солитонов [13, 14, 15] и называется электромагнитным солитоном конформноподобным электрону. Туннельная связь этих двух солитонов в расслоенном фрактальном гиперкомплексном пространстве в проекции на 4-х мерное пространство-время задаётся тензором энергии-импульса (тензором натяжения Максвелла вакуума) в правой части упомянутых уравнений упругости вакуума, причём тензор-потенциал электромагнитного поля входит как блок–матрица в гиперпотенциал X, Y поля Янга-Миллса. В то же время динамический солитон строго детерминированно определён топологическим солитоном как его производная или поворот поля на p /2 в виде умножения на i.
Солитонное решение как особое решение нелинейного дифф. уравнения устойчиво на сепаратрисах фазового пространства динамической системы, кроме того как всякое автомодельное, волновое решение оно удовлетворяет соотношениям на характеристиках (СОНАХАР), поэтому дифференциальное условие особенности (ДУОС) солитонных уравнений на характеристическом конусе совпадает с СОНАХАР. Применительно к уравнению ВАКЖОТ эти ДУОС выполняются тождественно в силу того, что ДУОС имеют вид 1-форм (именно точных и замкнутых форм) Картана, определённых на группе Ли симметрии этих уравнений, а так как присоединённое и коприсоединённое представлении групп Ли симметрии уравнения ВАГЖОТ в автодульном базисе гомологий и когомологий совпадают, то это представление становится неприводимым, поэтому выполняются тождественно и СОНАХАР, то есть их не надо задавать извне искусственно. Следует отметить, что изначальная точечная упорядоченность в накрывающем пространстве XM в процессе образования любого центрально-проективного пространства на сфере CPM-1 или RPM-1 полностью исчезает и наступает состояние детерминированного хаоса [16] характерного для всех солитонных динамических систем, поэтому факторпространство естественным образом становится пространством стохастических функций, а факторуравнение ВАГЖОТ вероятностным уравнением для функций плотности вероятности или квантоволновых функций. Однако в нелинейной системе с нелинейностью типа складки (x3 или sin(x)) в точках бифуркаций существует фазовый переход множества инстантонов в новое упорядоченное состояние называемое солитоном, причём белый шум инстантонов в результате нелинейного выпрямления становится коррелированным фликкер-шумом (или инфракрасной расходимостью в теории элементарных частиц [17]). Эффект стохастизации в проективных пространствах обуславливает существование топологически эквивалентных функторов, означающих тождественность геометрического, стохастического и вариационного описания физической реальности, что подробнее рассмотрено с следующей статье. Описанная общая концепция образования солитонов полностью отражена в частной задаче определения топологии ЭМ-солитонов, представленной в данной работе.
Используя указанные в [2] общие представления о топологии пространства АПК солитонов как геометрии вложений, определены топологические характеристики криволинейных симплексов-полиэдров с кручением по модулю два (mod2). Так степень гладкого отображения Deg2(xi(x)) на поверхности тора Мёбиуса (гиперфункции Морса букета торов) равна согласно [7, 12]
Deg2(xi) =iе16 sgn(det(dxi / dd j)) | mod2, (5)
где i =1 - 16 -- номер невырожденной особой точки.
При переходе через особую точку котензорного поля меняется его гомотопический класс [7], всего существенно различных классов 15 без учёта 1-ого тривиального тождественного класса, т. е. особые точки пересчитывают эти классы при непрерывном изменении параметров группы Ли, вычисленный ранг алгебры которой равен 16 [2]. Для комплексного представления тензорного поля его якобиан или гессиан положителен, поэтому для каждого гомотопического класса в (1) имеем
deg2(xi) =sgn(detc(dxi / dd j)) = (-1)2 = 1. (6)
По определению степень отображения скрученного симплекса есть эндоморфизм гомологии m-мерного пространства базы по mod2: Hm(S1n2, Z2) Ю Hm(S2n2, Z2) | mod2, где обозначено отображение одной части — S1n2 неориентированной гиперсферы типа «скрещенный колпак» локально изоморфной n-мерной поверхности слоя расслоенного пространства АПК на гиперлисте Мёбиуса на другую часть — S2n2 этой же сферы из всего букета торов Мёбиуса, кроме того в качестве коэффициентов инцидентности криволинейного клеточного симплекса-полиэдра берётся группа целых чисел Z2, которые пересчитывают локально два гиперлиста букета торов Мёбиуса. Прямое вычисление m-мерных гомологий Hm(X, W) тензорного поля и когомологий Hm(X, W) котензорного поля проводилось в комплексированном пространстве 2-форм Картана-Киллинга W =(Wc slWscg)c№ 0 и в комплексированной алгебры Ли симметрии солитонов с генераторами алгебры Xi = (Li)c из [2] с использованием производной Ли [18] по направлению векторного поля в связности Картана Di jk в проекцию на слой расслоенного пространства АПК солитона:
(LXD)i jk = dkj Xi + Xr dr Di jk - drXi Dr jk + djXr Di rk + dkXr Di jr. Тогда 2-коцепь алгебры Ли со значенями в W согласно [4] CD(X,Y)i j = (LX D)r ki(Ly D)k rj — (Ly D)r ki (LX D)k rj , применительно к пространству АПК солитона имеет кограницу по трём рёбрам (x,y,z) О X треугольного
гиперсимплекса этой коцепи d2CD(x,y,z) = 0 тождественно, то есть эта коцепь является коциклом-петлёй, поэтому по определению когомологии как фактор-алгебры коцикла по его когранице (идеалу) получается, что для ориентированных вещественных пространств (n-мерных сфер Sn) X = Sn при W = Z в классе целочисленных когомологий имеем
Hm(X, W) = Hm(Sn, W) = Hm(Rn, Z) = CD(X,Y) / dCD = 0 при n < m.
Это означает, что замкнутые в петли физические поля размерности n < m стягиваются в нуль вдоль расслоенного пространства АПК, поэтому все физические объекты состоящие из них неустойчивы и стабильно несуществуют. Для неориентированных вещественных пространств (n-мерных односторонних сфер Sn2 по mod2), когда X = Sn2, имеем
Hm(X, W) = Hm(Sn2, W) = Hm(RPn, Z2) = CD(X,Y) / dCD Ю Z2 при m < = n
в классе целочисленной группы W = Z2 когомологий по mod2. При этом для неориетированных пространств CPn (односторонних сфер комплексной размерности n), когда X = CPn [7]
Hm(X, W) = Hm(CPn, Z2) =CD(X,Y) / dCD Ю Z2, (по mod2) при m < = 2n
в классе целочисленных когомологий с кручением. Это означает, что существуют петли криволинейных клеток-полиэдров размерностей m < = 2n, которые триангулируют (покрывают сетью) всё пространство X = CPn, такие замкнутые петли физических полей (солитона) вещественной размерности m в неориентированном комплексно проективном пространстве нечётной размерности n затягиваются (заузливаются) в топологические узлы многолистников [10, 20] по n-мерному расслоенному пространству (аналогично двуоборотной петле на листе Мёбиуса), поэтому такие физические объекты устойчивы: электрон или ЭМ-солитон, протон, вихревые поля гиротропных ферримагнетиков, сверхпроводников и сверхтекучих сред, кручение жидкокристаллических нематиков, таких как высокомолекулярные полимеры (структуры ДНК) или жидкокристаллические глобулы металлоорганических калий-натриевых комплексов двойных углеводородных полиеновых цепей фосфолипидных мембран живых клеток с их электрон-вибронными колебаниями в виде двойных тороидально-вихревых солитонов-спайков нервных импульсов и др. Такое поведение (ко)гомологий:
(m < = n) е Z2Ь Hm(RPn, Z2) Ь Hm(X, W) Ю Hm(CPn, Z2) ЮZ2 ® (m < = 2n) Ѕ mod2, характерно именно для неориентированных комплексно проективных многообразий CPn нечётной размерности и вещественно проективных пространств RPn чётной размерности n. При этом каждому гомотопическому классу и изоморфной ему степени отображения
deg2(xi) = 1 согласно (5, 6) соответствует одна петля размерности от m до 2n включительно. Степень отображения deg2(xi) есть топологический индекс особой точки ind(d, x), он называется характеристикой c(x, G) векторного поля xi или вращением (наматыванием) векторного поля (слоя) вокруг всего физического пространства (базы) расслоенного пространства АПК на физической бесконечности [19]:
deg2x = ind2(d, x) = c(x, G) = c2(x, CPn) =1, Ѕ (mod2) (7)
где d -- параметры группы Ли. Это вращение в теории калибровочного поля является калибровкой тензорного (кирального) поля типа Янга-Миллса, при этом калибровка в солитонной теории называется инстантонами [19] тензорного поля солитона. Винтовое движение инстантонов в виде квантового туннелирования между сильно вырожденными энергетическими уровнями солитонов определяет их нетривиальное, топологическое взаимодействие, определяющее дополнительное сверхтонкое расщепление указанных уровней энергии солитонов и, как следствие, их взаимное затягивание-синхронизацию в пространстве и времени. Такое взаимодействие обуславливает калибровочно инвариантное, поэтому физически наблюдаемое, фазовое взаимодействие всех солитонных сущностей.
Вращение поля или турбулентный вихрь-петля [20], соответствующий deg2(xi) = 1, топологически устойчив, потому что для групп (ко)гомологий существует изоморфизм между гомотопическим классом, (ко)гомологией и фундаментальной группой петель
p(CPn, Z2) группы Ли: Z2 = Hm(CPn, Z2)Ы p(CPn, Z2) = Z2 (петля заузливается и затягивается). Турбулентный вихрь-петля, соответствующий deg2(xi) = 0, топологически неустойчив, так как 0 = Hm(CPn, Z2) Ы p(CPn, Z2) = 0 (петля стягивается в нуль и исчезает). Топологически устойчивые вихри (ферромагнетизма, сверхпроводимости, сверхтекучести, электрона, ЭМ-солитона) имеют «силу 1 / 2» [7], то есть при прохождении индикатора поля через центр вихря (листа Мёбиуса в дырке сферы Sm) направление или директор поля меняется на 2p / 2 = p в точном соответствии со свойством неориентированных пространств [21].
Благодаря автоморфизму солитонного решения относительно группы Ли симметрии солитонного уравнения: j(x) = G(j(x)) @ L (j(x)) или Ф = L (j(x)) — j(x) @ 0, вблизи нуля алгебры имеем ind(d, x) = ind(L,Ф) = ind(dL (j(x))/dj - 1) = sgndet(dL/dj - 1) = sgndetc(dL/dj - 1)= = (-1)2 = +1 (в комплексном представлении). Тогда полная степень отображения по mod2 в (1) в дополнение к (3) равна числу Лефшеца L2 равному количеству неподвижных точек группы Ли или числу гомотопически различных солитонных решений уравнений поля, это число равно 16-ти гомотопическим классам гомологии :
Deg2(xi) =c2(x, CPn) = L2 = iе16 sgn(det(dxi / dd j)) = iе16sgndetc(dL/dj - 1) = iе16 (+1) = 16. (8)
Ранг 16 алгебры G группы Ли симметрии распределяется следующим образом по рангам алгебр этих гомотопических классов:
rank(G) = rank(T) + rank(L) + rank(C) + rank(P) + rank(D) + rank(S),
-- rank(T) = 1 -- алгебры тождественного преобразования,
-- rank(L) = 1 -- ----»----- собственных вращений Лоренца,
-- rank(C) = 1 -- ----»----- конформного преобразования инверсии радиуса (1 / R),
-- rank(P) = 1 -- ----»----- нечётного количества инверсий знака координат,
-- rank(D) = 1 -- ----»----- преобразования дилатации,
-- rank(S) = 11 -- ----»----- преобразований крутильных сдвигов вакуума от дипольного до додекапольного (поэтому не случайно додекаэдр -- максимальная сингония кристаллов твёрдого тела). Но по определению характеристика Эйлера многообразия в (8) равна
c2(x, CPn) =16 = i=0е n (-1)i rank Ci(CPn, Z2) = i=0е n (-1)i dimHi(CPn, Z2), (9)
где Ci(CPn, Z2) -- коцепи триангуляции размерности i всего пространства CPn. Таким образом соотношение задаёт уравнение (ко)гомологий относительно неизвестной размерности n комплексно проективного пространства CPn солитона:
i=0е n (-1)i dimHi(CPn, Z2) = 16. (10)
Известно [21], что Hi(CPn, Z2) = 0 при i № 2n, но Hi(CPn, Z2) = Z2 при i < = 2n. Как указывалось выше число i пересчитывает все 16 гомотопических класса симметрии солитона в комплексном пространстве представления гомологии. Поэтому для размерно-однородных полиэдров триангуляции, у которых i-мерная грань есть точное ребро приклеенного полиэдра размерности i +1 (которые только и рассматриваются в данной работе), имеем равенства [7]:
dimHi(CPn, Z2) = 1, при i = 0, но для i № 0 dimHi(CPn, Z2) = 1, 3, 5,... -- всего n размерностей для нечётных i, dimHi(CPn, Z2) = 2, 4, 6,... -- всего n размерностей для чётных i, то есть всего различных значений размерностей Hi(CPn, Z2) равно 2n, это — размерность вещественно проективного пространство RP2n вложений CPn. Тогда знакопеременная конечная сумма членов арифметической прогрессии в (9) равна:
i=0е n(-1)i dimHi(CPn, Z2) = (-1)0 1 + (-1)1 1 + (-1)2 2 +... + (-1)2n-1 (n-1) + (-1)2n n = 16 или
i=0е n(-1)i dimHi(CPn, Z2) =1 + n (n + 1) — n2 = 16, откуда n (n + 1) — n2 = 15 или n = 15.
Таким образом проективно комплексное пространство CPn = CP15 должно иметь нечётную размерность 15, тогда в него гладко вкладываются все подпространства триангуляции криволинейными полиэдрами в виде букета торов Мёбиуса, на которых располагаются поля ЭМ-солитона или электрона-солитона, то есть может существовать вообще солитонное решение нелинейных уравнений триединого поля, что и требовалось доказать. В свою очередь пространство CP15 гладко вкладывается в комплексное (псевдоевклидово) пространство C16 Ю CP15, но пространство C16 изомофно бигексанионному пространству H8: C16 Ы H8, поэтому в кватернионное пространство H8 гладко вкладывается кватернионо проективное пространство HP7: H8 Ю HP7. Следовательно существует следующая топологическая схема, используемая для построения (ко)гомологических цепных последовательностей фрактальной геометрии солитонов: CP15 Ь C16 Ы H8 Ю HP7. В свою очередь гиперкватернион H8 размерности 8 расщепляется по редукции на два сопряжённых гексаниона H4 размерности 4: *H4 Я H8 Я H4, в полном соответствии с расщеплением первого неприводимого тензора кручения Картана в [2, 22], локально на каждом гиперлисте Мёбиуса размерности 8. Кватернион H8 или H4 определяет пространство глобального вложения указанного букета 3-мерных четырёхзаходных 4-х торов Мёбиуса, однако локально в физической точке наблюдается лишь один из торов одного из заходов, на одном каком-нибудь 3-мерном листе (правой или левой ориентации) с ортогональном ему осью собственного времени. Такое 4-мерное комплексное пространство каждого захода изоморфно пространству одномерных кватернионов H1, поэтому по количеству заходов H4 имеет редукцию *H1 Я H4 Я H1. То есть кватернион H1 определяет локально (по алгебре) существование физически наблюдаемого именно 4-х мерного пространства-времени, в котором и действует группа Лоренца L4 изоморфная H1. Поэтому существует следующая топологическая схема:
наблюдаемый антимир е L4 Ы*H1 Я *H4 Я H8 Я H4 Я H1Ы L4 ® наблюдаемый мир.
Важно отметить, что существование каждого из двух сопряжённых *H4, H4 кватернионов на соответствующих двух гиперлистах Мёбиуса с противоположной ориентации реперов-тетрад, например при смене направления оси времени, отвечает рождению двух дуально сопряжённых ЭМ-солитонов или пары электрона-солитона и позитрона-солитона с противоположным течением собственного времени. При этом течение абсолютного времени вакуума есть процесс самодвижения (автоморфизма) фазированных солитонных замкнутых вихрей-узлов криволинейных полиэдров триангуляции квантов пространства АПК размером ~ 10 -33 см в виде букета торов Мёбиуса вдоль одного действительного орта кватерниона H1, три мнимых орта определяют сигнатуру наблюдаемого 3-х мерного плоского физического пространства.
В соответствии с общей теорией картановских полалгебр [25, 26] алгебра A(L) солитона имеет следующее разложение в прямую сумму алгебраических подпространств:
A(L) = {Q[(0) Е Ao Е Aa] ОA Ы TGS(L)}, (11)
где Ao — некоторая картановская подалгебра,
A(L) Й Ao = {y ОA(L) : [y, ji ] = 0, $jiО A(L), i = [1, 2,... M] };
при этом корневое подпространство определяется базисом
Aa №(0),
Aa = {y ОA(L) : [y, ja ] = a(y) Ч ja, $ jaО A(L), a(y)О D (a) = [+ (N — M) / 2]};
Q — квантор всеобщности элементов алгебры ЭМ-солитонов,
y - линейная комбинация всех N = 20 генераторов алгебры Ли или всех
компонент тензора Картана-Риччи (4 трасляции по базе не рассматриваются),
a(y) № 0, корень алгебры A(L) относительно Ao,
Ab - вектора корневого подпространства алгебры Картана, причём
b = 0, a, где a = + 1/2, + 1, + 3/2, + 2,... + (N — M) / 2,
M = число независимых элементов алгебры A(L) (её ранг),
D (a) = {a} = [+ (N — M) / 2] — множество ненулевых простых корней алгебры A(L).
Ранг М = 16 с учётом тождественного преобразования, причём в соответствии с теорией Картана-Вейля он равен полной размерности группового подпространства картановской подалгебры, а значит сумме размерности d её тороидальной части, то есть замкнутого тора, и размерности d её векторной части, то есть — расщеплённого тора или гиперболоида в локальном гиперкомплексном пространстве 16 измерений, тогда М = 2 Ч d .
Размерность М не зависит от выбора самой картановской подалгебры. Поэтому локальная размерность d тора Мёбиуса устанавливается по рангу глобальной алгебры L k равному рангу локальной алгебры A(L k). Важно отметить, что ранг 16 совпадает с числом независимых параметров или операторов классической 15-параметрической алгеброй конформной симметрии С(15) плюс тождественное 1-преобразование, которая является накрывающей для алгебры sl (2, C). Последняя — образуется в результате редукции A(L k), как обёртывающей алгебры для фактор-алгебры A(L ) / r(L), на свои линейные подалгебры:
A(L k) Я = red A(L ) = gl (n, C) Я sl (n, C) Я su (n, C) Я u (n, C) и т.д.
Что является не случайным фактом, а обусловлено существованием преобразования проективно кватернионного пространства АПК HP7 на касательное псевдоевклидово пространство Е4, в котором локально действуют указанные линейные подалгебры.
Известно [25], что векторная часть картановской подалгебры имеет автоморфизмы, порождённые группой Вейля в виде перестановок, отражений и инверсий базисных векторов Aa корневого пространства Картана в (11). Этот факт означает такую же симметрию относительно правых-левых систем координат базисных вектор-функций канонических координат в пассивной концепции представления групп преобразований применительно к подпространствам Картана. Указанная симметрия передаётся на всё групповое пространство TGS(L) через его алгебру A(L ) в [2.40], благодаря такой симметрии одностороннего тора правые локальные системы координат могут непрерывно трансформироваться в левые локальные координаты при глобальном движении по поверхности одностороннего тора.
Рассмотрев различные точки зрения на локальную область базы и слоя (топологическое групповое пространство (TGS) солитона), как комплексную гиперповерхность 16 измерений C16 (или 32 вещественных измерений), можно сказать, что тороидальная часть (замкнутый «лемнискатный» тор Мёбиуса) имеет локально комплексную размерность 8 для H8, а векторная часть в виде расщеплённого на бесконечности гиперболического тора Мёбиуса (экстравертивного или конформно преобразованного лемнискатного тора) имеет локально комплексную размерность равную 8. Тогда в точках этих торов существуют как-бы две стороны или два локальных репера сопряжённой комплексной размерности 4 для H4 двух обычных псевдоевклидовых пространства-времени Минковского. Эти реперы имеют противоположную ориентацию (например во времени), соответствующую локально двум сторонам гиперлиста Мёбиуса или частице и античастице.
Более того в малой области гиперболическая геометрия векторной части конформно-подобна плоскому псевдоевклидову пространству (как стереографическая проекция) Е8 двух спаренных реперов или пространству 4 комплексных измерений Е4 для одного репера. По различным нелинейным представлениям группы симметрии пространства Е8 классифицируется структура элементарных частиц в разных современных теориях единого поля.
Поскольку тороидальная и векторная части симметричны относительно конформного интровертирования или экстравертирования торов Мёбиуса, то базой пространства АПК можно считать замкнутый тор (в котором выколот центр), а слоем — векторное пространство (разомкнутый тор на бесконечности), но можно наоборот считать замкнутый тор слоем расслоенного пространства АПК или внутренним групповым пространством частиц-солитонов, тогда векторная часть (разомкнутый тор) это база АПК или обычное внешнее Е4 физическое пространство-время Минковского, в котором действует группа Лоренца и наблюдаются физические явления электродинамическими методами. Выбор базы или слоя зависит от степени микро или макроскопичности задачи, области формулирования задачи в физике, биофизике, биологии или техники, а также от приемственности методов решения её и принятых схем измерения.
Исследование картановской подалгебры в базисе Картана-Вейля позволило определить собственные значения проекций угловых моментов (спинов) триединого поля ЭМ-солитона на физически фиксированное направление в пространстве в виде направления движения центра масс солитона. Движение солитона рассматривается как его групповой автоморфизм в пространстве АПК, пространстве, которое и создаёт солитон вокруг себя.
Алгебра Картана в ортонормированном базисе Картана-Вейля
{ 1, ji, ja} (12)
в соответствии с теоремой Шевале [25] имеет вид :
м {1},
ч [ji, jj] = 0,
ч [ji, ja] = aЧ ja,
ч [ja, j-a] = ji,
ч [ja, jb] = Ngab Ч jg,
о a, b, g, = { + (N — M) / 2} = + 1/2, + 1, + 3/2, + 2, (13)
где
{1}- единичная матрица тождественного элемента группы (для глобальной группы
это трансляционное, инстантонное преобразование симметрии солитона),
i, j = 1, 2,... М,
М = 16 — ранг алгебры,
a, b, g, О D (a) = {a}- система простых корней (подлежит определению),
[ja, j-a] = 1 - нормировка Шевале,
Ngab = + (р -1) — целые числа, константы Картана,
Ngab = — Ngba -- свойство антисимметрии структурных констант Картана.
Величины ja являются операторами рождения-уничтожения ЭМ-солитона из физического сверхплотного вакуума полей натяжения Максвелла, кривизны Римана-Эйнштейна и кручения Картана-Риччи; знаки корней a, b, g определяют систему координат (отсчёта) солитона : (+) правую систему координат и правую поляризацию вакуума, (-) левую систему координат и левую поляризацию вакуума. Коммутационное соотношение [ja, j-a] = ji в (9) определяет непрерывный переход от правой системы координат к левой в односторонней 4-поверхности тора Мёбиуса, а так же от правой поляризации вакуума к левой, от проекции спина (+) к проекции спина (-), от материи (+) к антиматерии (-), то есть это соотношение описывает трансмутацию электрона в позитрон, нейтрино в антинейтрино, солитона в антисолитон самодуальный солитону и т.д. Величины
a = 0, + 1/2, + 1, + 3/2, + 2 (14)
определяют собственные значения проекций спина четырёх возможных видов полей ЭМ-солитона, а именно a = + 1/2 — типа электронного нейтрино, a = + 1 — фотона,
a = + 2 — гравитона, a = + 3/2 — полный спин гравитино или мюонного нейтрино, ориентированный под углом к направлению движения, имеющий фотонную проекцию + 1 на базу и нейтринную проекцию + 1/2 [2] на слой расслоенного пространства АПК (где база и слой понятия относительные). В присоединённом представлении алгебры A(L k) структурные константы Картана Ngab равны стуктурным константам Ли в [2.22] в виде тензоров кручения Картана-Риччи или матричным компонентам j(ga)b Ы jb в (13) для операторов рождения-уничтожения ЭМ-солитонов в собственном спинорном по индексу b представлении:
Ngab = W gab = j(g a)b. (15)
Присоединённое представление в форме соотношений (13) упрощается до замкнутых комбинаций целых чисел и становится жёстким соотношением, не допускающим ни каких априорных констант: все числа определены в нём самом, причём Ngab, W gab, j(g a)b целочисленные функции a данные в (14).
Как указывалось выше алгебра поля ЭМ-солитона изоморфна алгебре Ли симметрии его пространства АПК. Поэтому ЭМ-солитон уникален тем, что является частицей-полем, геометрией и индуктором пространства-времени в совокупности как пространство АПК. При этом движение солитона, являясь автоморфизмом группы Ли его симметрии, описывается присоединённым представлением этой группы, а значит и группой гомологии.
Четырёхмерность пространства АПК ЭМ-солитона объясняется кроме указанной выше глобальной топологической причины, ещё и локальной причиной.
Указанная выше подалгебра Вейля W действует в базисе корневых векторов j(ga)b Ы jb Картана-Вейля [25, 26], которые удовлетворяют соотношениям:
jgg = 1, (ja, jb) m (a, b) = 1, m(a, b) = 2, 3, 4,....
Поэтому подалгебра W изоморфна алгебре симметрии всех подстановок базисных корневых векторов jb, а так же отражений и инверсий правой в левую систему координат с ортами в виде векторов jb.
Характеристический полином алгебры Картана-Вейля (13) имеет степень
N — M + 1 = 4 + 1 = 5, так как кроме 4 спиновых чисел система коммутаций (13) содержит корень a = 0, соответствующий инстантону - тождественному преобразованию {1} группы Ли или {0} её алгебры, неучитываемой по определению в алгебре Картана (см. условие Aa №(0) в системе равенств (11)). Тогда этот полином имеет вид:
a Ч(a — 1 / 2) Ч (a — 1) Ч (a — 3 / 2) Ч (a — 2) = 0, (16)
а так как все вектор-корни простые, этот полином является и минимальным аннулирующим полиномом той же степени 5. Поэтому интерполяционный матричный полином Лагранжа-Сильвестра на множестве корней a подалгебры Картана в базисе Картана-Вейля имеет степень 5 — 1 = 4. В экспоненциальном отображении глобальной группы Ли (в матричном представлении M (A) алгебры A(L)) этот интерполяционый полином даётся формулой:
exp(M(A)) = so Ч{1} + s1Ч M(A) + s2Ч M2(A) + s3Ч M3(A) + s4ЧM4(A), (17)
где si — интерполирующие матричные полиномные множители Лагранжа. Подалгебра Вейля определяет симметрию подстановок корневых векторов ja в корневом пространстве Картана, но эти подстановки идуцируют изоморфные подстановки a — корней в интерполяционном и характеристическом полиноме.
В свою очередь эта симметрия подстановок корней в полиноме изоморфна группе Галуа, которая алгебраически разрешима [27] в поле рациональных операций для полиномов степени < 4. Но интерполяционный полином (17) как раз имеет степень 4, а значит он разрешим на спектре матрицы M (A), то есть на корнях алгебры A изоморфной алгебре Картана при любых интерполяционных матричных коэффициентах si . Таким образом существует изоморфизм подалгебры Вейля W, алгебры перестановок корней в (16, 17) и алгебры Галуа. Но такой изоморфизм, в связи со всем выше сказанным, обнаруживается именно в 4-х мерном пространстве ЭМ-солитона на 4-х мерном торе Мёбиуса. Разрешимость алгебры Галуа с геометрической точки зрения означает возможность построения с помощью линейных мер: циркуля и линейки, любых геометрических объектов, измеряемых электродинамическими методами. Эти геометрические объекты по сути своей являются электродинамическими объектами физики, биофизики, биологии, техники именно в 4-х мерном пространстве. То есть все эти объекты можно вычислить алгебраически (в конечном счёте), как корни интерполяционного полинома (17) четвёртой степени, но с различными коэффициентами интерполяции si в зависимости от природы задачи. Других простых корней, а значит других полей, атомов, молекул, частиц и т.д. сводимых к ЭМ-солитонам именно в 4-х мерном пространстве-времени не существует в принципе. Можно сказать другими словами, что пространство-время потому и 4-х мерно, что только его геометрические характеристики можно выразить алгебраически в поле рациональных операций и извлечения корней из заданных чисел, соответствующих отрезкам прямых. И наоборот, чтобы представлять геометрические и им эквивалентные электродинамические объекты с помощью линейных мер, рациональных операций и извлечений корней, пространство обязательно должно быть 4-х мерным. В пространствах иных измерений, характеристические и интерполяционные полиномы будут высших степеней и корни их, как инварианты подгруппы Вейля, определяются аналитически, но уже не алгебраически, а в виде решения бесконечно-зацепляющихся линейных дифференциальных уравнений в частных производных первого порядка Пфаффа. Эти решения не возможно принципиально представить алгебраически, а значит изобразить геометрически с помощью линейных мер. Физические объекты, описываемые этими высшими симметриями будут ненаблюдаемыми существующими электродинамическими экспериментальными методами.
Решение солитонных уравнений инвариантное относительно только группы (алгебры) Ли строится по генераторам этой группы в экспоненциальном отображении её гиперкомплексной алгебры, заданной в присоединённом представлении на базисе Картан-Вейля. Оно имеет вид следующих матричных элементов смешанных (по индексам b, g) спиноров.
j(g b) = exp[exp(dnm xm + dn) Ng n b]. (18)
Это решение определено на структурных константах Картана (15), а следовательно на корнях подалгебры Картана ЭМ-солитона.
Указанная выше в [2.33] кватернионная гиперкомплексификация означает, что для операторов алгебры в (13) введено представление
dk = Re(d k) + Im(d k) = mod(d k) (cos fk + iksin fk) = Rdk + ikIdk,
dkm = mod(dkm)(cosfkm + iksin fkm) = Rdkm + ikIdkm,
где по индексу k нет суммирования,
ik = i0, i1, i2, i3 = (- 1)1/2 ортогональные мнимые единицы схемы кватернионной комплексификации, а fkm — углы-матрицы фазы симметрии.
В общем схема гиперкомплексирования с помощью кватернионов или пошагового удвоения размерности комплексного числа однотипна как для вектора Zn = (dk, dkm) групповых параметров, так и блочного вектора физических значений полей (слоя расслоенного пространства)
Zn =(Fc s, Rscsl, Wc sl)т Ы Z0, Z1, Z2,...Zn ,
или 4-мерного физического пространства (базы)
Zn =(x0, x1, x2, x3)
Z0 = ao + 0 Ч i1
Z1 = a1 + a2 Ч i2 = А1, 2 = 11 Ч a1 + J1 Ч a2, где
число i1 -- мнимая единица (i12 = -1),
матрицы а n -- блочно-диагональные, n = 0, 1, 2,...N шаг комплексирования, блочные матрицы А1, 2 , 11, J1 равны:
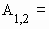
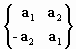 ,
, 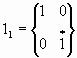 ,
, 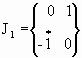 ,
,
11 -- оператор-матрица тождественного преобразования,
J1 -- оператор-матрица мнимой единицы,
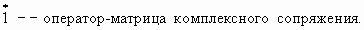
Тогда например
Z2 = (a1 + a2 Ч i2) + (a3 + a4 Ч i2) Ч i3 = a1 + a2 Ч i2 + a3 Ч i3 + a4 Ч i4 =
= 12Ч (a1 + a2 Ч i2) + J2 Ч (a3 + a4 Ч i2) = 12 Д А1, 2 + J2 Д А3, 4 =
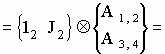
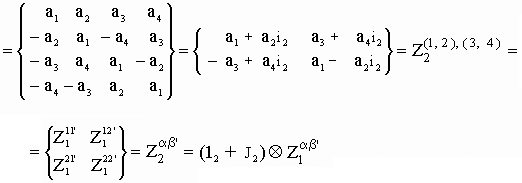
где
знак + тензорной суммы матриц,
знак Д означает кронекеровское произведение матриц,
i22 = -1, i32 = -1, i4 = i2 ґ i3 = -1,
гиперкомплексное число Z2 в спинтензорных компонентах Z2a b’ в виде проекций на две гиперплоскости комплексного пространства имеет составные (как функция размерности n) спинорные штрихованные и нештрихованные индексы a = (1, 2); b’= (3, 4). Следовательно для n-мерного комплексного пространства n-шага комплексирования кватернионы в гиперспинорной форме всего расслоенного пространства (например кватернионно проективного пространства HPn) порождают рекуррентное соотношение:
Zna b’ = (1n + Jn) Д Zn -1a b’, (19)
где пара индексов ab’ -- функция n. То есть согласно [34]
a Ю ((((1,2),(3,4)),((5,6),(7,8))),...,(((n-3),(n-2)),((n-1),(n)))),
b’ Ю ((((n+1),(n+2)),((n+3),(n+4))),...,(((2n-3),(2n-2)),((2n-1),(2n)))).
Любые дифференциальные уравнения, определяющие эволюцию тензора Zn, решаемые итерацией имеют вид:
Zm = Zm-1 + f(Zm-1), (20)
где m -- шаг итерации. На каждым шаге n комплексирования в (19) можно выполнить m итераций согласно (20) и наоборот: на каждом шаге m итерации (20) можно выполнить n шагов гиперкомплексирования, что даёт один и тот же результат по вычислению именно солитонного решения
(Zna b’)mg d’ = (Zmg d’)na b’, (21)
то есть операции по индексам [na b’], [mg d’] коммутируют.
Доказательство этого факта заключается в следующем, подставив (20) в (19) имеем
(Zmg d’)na b’ = (1n + Jn) Д (Zmg d’)n -1a b’ или
(Zm-1g d’ + f(Zm-1g d’))na b’ = (1n + Jn) Д (Zm-1g d’ + f(Zm-1g d’))n -1a b’ (22)
подставив (19) в (20) имеем
(Zna b’)mg d’ = (Zna b’)m-1g d’ + f((Zna b’)m-1g d’) или
((1n + Jn) Д Zn -1a b’)mg d’ = ((1n + Jn) Д Zn -1a b’)m-1g d’ + f(((1n + Jn) Д Zn -1a b’)m-1g d’) (23)
из (22) имеем
(Zm-1g d’)na b’+ (f(Zm-1g d’))na b’ = (1n + Jn) Д (Zm-1g d’)n -1a b’ + (1n + Jn) Д (f(Zm-1g d’))n -1a b’
или с учётом (19) получаем
(1n + Jn) Д (Zm-1g d’)n -1a b’ + (f(Zm-1g d’))na b’ = (1n + Jn) Д (Zm-1g d’)n -1a b’ + (1n + Jn) Д (f(Zm-1g d’))n -1a b’,
где действие индексов [n -1a b’] равно ((1n + Jn))n -1a b’ = 0,
и после сокращений подобных членов имеем
(f(Zm-1g d’))na b’ = (1n + Jn) Д (f(Zm-1g d’))n -1a b’, (24)
что означает автоморфизм оператора уравнения f(Zm-1) (в конечных разностях) относительно группы гипервращений, образующей кватернионно проективное пространство HPn = HP15 солитонов;
из (23) с учётом (20) имеем
(1n + Jn) Д ((Zn-1a b’)m-1g d’ + f((Zn-1a b’)m-1g d’)) = ((1n + Jn) Д Zn -1a b’)m-1g d’ + f(((1n + Jn)Д Zn -1a b’)m-1g d’)
и после сокращений получаем
(1n + Jn) Д f((Zn-1a b’)m-1g d’)) = f((1n + Jn) Д(Zn -1a b’)m-1g d’), (25)
это означает коммутативность оператора f(Zm-1) (операции взятия границы dZm цепи) и гиперкомплексирования, например в кватернионно проективном пространстве HPn = HP15 группы (ко)гомологии солитонов, что завершает доказательство коммутативности в (21).
Поэтому существует коммутативная топологическая диаграмма морфизмов:
dZm
Zm Ь Zm-1
f(f...f(Zn)) = dZm — nЭЭ (1m-1 + Jm-1) Д (1m-2 + Jm-2) Д ...Д (1n-1+Jn-1) = k=n-1Хm-1(1к+Jк)
Zn Ь Zn-1
(1n + Jn) Д (26)
это означает, что (m — n) шагов итераций-дифференцирований эквивалентно (m — n) шагов гиперкомплексирований или поворотов в гиперкомплексных фрактальных пространствах (m ґ n) измерений. В основе образования топологической схемы (26) лежит топологическая коммутативная схема автоморфизма и инвариантности солитонных функций относительно группы Ли симметрии солитона, указанная в [2. 8, 2.10]: расслоенное пространство АПК L-- первое продолжение дифф. оператор солитонного уравнения
G(j(x, Г,Т)) = G(j) Ь G(x) = (x, Г,Т) -- расслоенное геометрическое пространство
G--расслоение поляЭ Э G-- расслоение геометрии, отображение сечения}гомология
слой --j(x) Ь x -- база
L -- дифф. оператор солитонного уравнения (27) Морфизм (26)
{[f(f...f(Zn)) = dZmґ n]Ч[(1n + Jn) Д]} = [(1m-1 + Jm-1) Д (1m-2 + Jm-2) Д... Д(1n-1 + Jn-1) =
= [k = n-1Хm-1(1к + Jк)] Ч dZm О Mor (Zn-1, Zm)
и морфизм (27)
{L ЧG} = GЧL О Mor (x, G(j))
в совокупности определяют существование функтора F фрактализации
F: Mor (x, G(j)) Ю Mor (Zn, Zm),
из категории гомологий (топологического множества) в категорию итераций гиперкомплексного группового пространства или в категорию фрактализации, где существует солитонное решение дифференциального уравнения (т.е. в пространство гомотопических групп). Известно [20], что кронекеровское произведение матриц, когда матрицы являются стохастическими, осреднённое с некоторой плотностью вероятности w, определяет матрицу ковариации стохастического процесса. Применительно к данной нелинейной системе уравнений солитона [2.1, 2.2, 2.27] или (20) в ней неизбежно наступает состояние детерминированной стохастизации [16, 9, 28] поля и геометрии путём перемешивания гармонических и частотных составляющих солитонного пакета волн по причине их нелинейного взаимодействия (по цепи обратной связи) в полосе частот и длин волн солитона.
Процесс детерминированной стохастизации естественным образом порождает фрактальное (хаусдорфово) множество. Тогда математическое ожидание от всех уравнений солитона (19, 20) имеет стандартный вид:
M[Zna b’] = M[(1n + Jn) Д Zn -1a b’] = vт Zn(y) Ч w(y, s) ds,
M[Zmg d’] =M[Zm-1g d’ + f(Zm-1g d’)] = vт Zm(y) Ч c(y, s) ds,
здесь важно отметить, что интегралы по объёму расслоенного пространства солитона однозначно определяются, так как это пространство является пространством абсолютного параллелизма с кручением (по mod2), где правая и левая ивариантная мера Хаара совпадают, хотя алгебра Ли его симметрии не коммутативна. Многомерная (n,m-мерная) плотность вероятности w(y, s) или c(y, s) удовлетворяет стохастическому уравнению Колмогорова-Фоккера-Планка [29] для этих плотностей вероятностей с мат. ожиданиями M[Zna b’], M[Zmg d’] и дисперсиями M[Zna b’]2, M[Zmg d’]2. Стохастизация SG группы Ли понимается как объединение SG = ИGk из N — случайных реализаций всех параметров группы (которые корреляционно независимы) по различным размерностям фрактального множества в каждой точке базы при этом среднее значение группы
M[G] = (1/N) ЧеNk=1(nk Ч Gk),
где N -- максимальная размерность фрактального множества, — подлежит определению (см. ниже),
nk -- число реализаций группы (частота) в размерности k-го фрактального множества (например в размерности 1, т.е. в 1-ой криволинейной клетке-полиэдре триангуляции в виде букета 4 торов Мёбиуса n1=1, в размерности 2, т.е. в 2-х клетках фрактальной триангуляции n2=2 и так далее до размерности N в N клетках триангуляции nN = N),
nk / N -- относительная вероятностная частота. Тогда топологическая диаграмма (27) примет вид
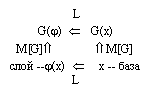 (28)
(28)
с законом коммутации M[G] Ч L1 = L Ч M[G], где оператор L дифференциального солитонного уравнения является детерминированным оператором.
Стохастизация группы индуцирует новую категория случайных пространств, морфизм которых даётся коммутационной диаграммой (28):
L(M[G(x)]) = {M[G] Ч L}(x) О Mor(x, SG). (29)
В свою очередь морфизмы Mor (x, G(j)), Mor (Zn, Zm) в (26, 27) в совокупности определяют новый функтор S-детерминированной стохастизации, существование которого доказывается следующим образом. Используя левую часть коммутации (29) и свойство произведения детерминированного оператора L и ожидания M[G(x)] имеем:
L(M[G]) = M[L(G)], тогда применяя морфизм Mor (Zn, Zm) гиперкомплексирования аналогично (19, 20, 22) получим L(M[G]) = M[L(G)] = M[Lmg d’ Ч Gna b’]. Поскольку гиперкомплексированные операторы солитонного уравнения и его группа симметрии коммутативны, а оператор L автоморфен, что доказано в (24, 25), то имеем:
L(M[G]) = M[L(G)] = M[Lmg d’ Ч Gna b’] = M[Gna b’ Ч Lmg d’] = M[Lmg d’],
но определённый выше оператор осреднения M[…] действует на детерминированный оператор L, фрактализованный гиперкомплексированием Lmg d’, следующим образом:
M[Lmg d’] = еNk=1((nk/N) Ч Lmkg d’),
и, если обозначить (nk/N) = z -k в качестве коэффициентов решётчатого z-преобразования Лапласа импульсных функций, то получим
M[Lmg d’] = еNk=1((nk/N) Ч Lmkg d’) = еNk=1(z -k Ч Lmkg d’) = Lmg d’ (z)
есть конечное z-преобразование гиперкомплексированного солитонного оператора Lmg d’, что означает эквивалентность с точностью до равенства
L(M[G]) = Lmg d’ (z). (30)
То есть действие стохастизации SG на группе симметрии солитонного уравнения эквивалентно z-преобразованному по Лапласу дифференциальному оператору этого же уравнения. Этот более общий вывод соответствует частному результату Гренандера [30]: броуновское блуждание точки на группе дробно-линейных преобразований
y = (ax+b)/(cx +d)
или на круговых орбитах плоскости Лобачевского, являющейся нелинейным представлением унимодулярных линейных групп, в частности симметрии дифференциального оператора Лапласа D, порождает этот же оператор, но уже индуцированный уравнениями Колмогорова-Фоккера-Планка, действующий на пространственноподобной поверхности или оператор Даламбера на времениподобной поверхности пространства-времени Минковского.
Таким образом равенство (30) отождествляет геометрию и вероятность. Это отождествление согласно (30) и доказывает существование функтора S-детерминированной стохастизации, который действует из категории фрактализации (или итераций солитонного уравнения) в категорию случайных пространств:
Mor (Zn, Zm) Ю Mor(x, SG).
Совокупность функтора фрактализации F и функтора стохастизации S, обуславливает наличие короткой точной топологической последовательности
F S
Mor (x, G(j)) ЮMor (Zn, Zm) ЮMor(x, SG),
а значит и ретракции (продолжения) функторов в виде их произведения FЧS:
(F S)
Mor (x, G(j)) Ю Mor(x, SG), так как функторы F и S независимы и следовательно коммутативны. Поэтому существует замкнутый топологический цикл [33] ковариантных функторов [7]:
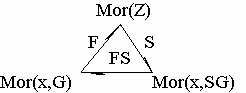 , (31)
, (31)
который позволяет проводить вычисления в любой из этих категорий в зависимости от набора конструктивных методов, формул или приёмов (дифференцирования, интегрирования), но результат будет справедлив сразу для всех многообразий (данного цикла) различного квантора общности (метрические пространства, пространства хаусдорфа, группы, групповые пространства, гомологии групп, топологические последовательности и множества, топологические спектральные последовательности и др.). Более того благодаря циклическому функтору (31) (функтору тавтологии или тождественной истинности) вычисление спектральной последовательности (ко)гомологий n-ранга расслоенного итерированием и гиперкомплексированием пространства АПК редуцируется к спектральным последовательности первого ранга, но в стохастическом групповом пространстве, при этом эйлеровы классы сводятся к классам Чженя, а топологическая спектральная последовательность для этих характеристических классов приводится к тавтологической точной последовательности произведений Уитни [31] (как частный случай изоморфизма Тома) при вычислении вероятностей. Что подробнее описано далее.
Например для вычисления числа N -- размерности фрактального множества используется комбинаторная аппроксимация гомотопий [7] расслоенного пространства АПК различными сочетаниями групп Лоренца-Пуанкаре, причём правильность конечного результата применительно к солитону контролируется конкретными физическими сопоставлениями. Именно такая аппроксимация допустима по причине того, что каждый из указанных морфизмов согласно (31) представляет собой объединение базы и слоя, то есть является частным случаем общего морфизма Mor(Im x n, dIm x n), как категории топологического множества объединения куба IN и некоторой его границы dIN:
Mor (x, G(j)) ~ Mor (Zn, Zm) ~ Mor(x, SG) Н Mor(Im x n, dIm x n).
Причём факторпространство IN / dIN гомеоморфно сфере SN (по mod2 для пространств с кручением). Поэтому существует [31, 32] общий функтор C для функторов F, S, FS такой, что
C: Mor(Im x n, dIm x n) = Mor(IN, dIN) Ю Mor(SN, x0)
то есть отображение Mor(IN, dIN) в сферу SN (можно и по mod2) с отмеченной точкой x0 (единицей группы) на ней. Но на сфере существует группа конформных преобразований C(N) (как стереографическая проекция SN на CPN-1 [31]) изоморфная для случая C(15) группе Лоренца-Пуанкаре по своей алгебре. В группе Лоренца-Пуанкаре как известно содержится подгруппа собственных вращений Лоренца пространства Минковского.
Все фрактальные множества строятся единообразно для цепей или (ко)гомологий путём рекурсии коммутативной диаграммы (27, 28). Например, топологическая последовательность операторов расслоений определяется как
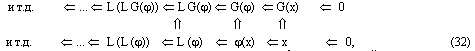
она порождает топологическую последовательность k-мерных цепей симплекс-полиэдров Ск триангуляции расслоенного пространства АПК:
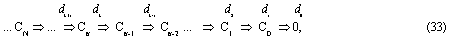
где операторы границы (дифференциирования) dk удовлетворяют условиям dk-1dk= 0 (граница границы равна нулю), группа k-мерных циклов (петель вихрей) определена как ядро гомеоморфизма Ск в Ск-1, образующие подгруппу в Ск: Ker dk = {cОСк: dkc = 0}; группа k-мерных границ (в виде знакопеременной суммы (k-1)-мерных граней k-полиэдра) как образ гомеоморфизма Ск в Ск-1, образующие подгруппу в Ск:
Im dk+1 = {cОСк: c = dk+1Сk}.
Изоморфизм цепного комплекс (33) в факторгруппу Ker dk / Im dk+1, то есть гомологию Hk(C*, G) в (9, 10), образует гомологическую последовательность де Рама (для проекций из расслоений):
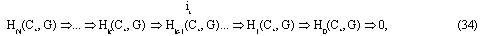
или когомологическую последовательность (для поднятий в расслоения с помощью контрвариантных функторов) при смене направления стрелок:
HN(C*, G) Ь... Ь Hk(C*, G) Ь Hk-1(C*, G)... Ь H1(C*, G) Ь H0(C*, G) Ь 0.
где ik изоморфизм вложений, C* = Xn -- n-мерное пространство группы Ли симметрии солитона, G = Z2 -- абелева группа вычетов по mod2 для полиэдров с кручением. Поэтому существует последовательность гомеоморфизмов:
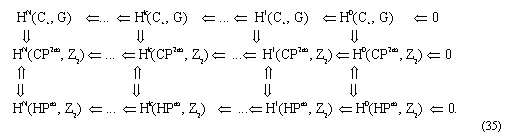
Используя известный факт [7], что на категории пар компактных полиэдров (букете 4-х торов Мёбиуса) сингулярная (с кручением полиэдра) и симплициальная (без кручения) теории (ко)гомологий почти совпадают, из длинных последовательностей (34, 35) извлекается точная подпоследованость Майера-Виеториса:
...ЮHk+1(S4m+1,Z2) ЮHk(S4m+1=CP2mИCP2m,Z2) ЮHk(CP2mЗCP2m,Z2) ЮHk(CP2mЕCP2m,Z2) Ю
ЮHk(CP2m,Z2)ЕHk(CP2m,Z2) Ю Hk(CP2m=S4m+1,Z2) ЮHk-1(CP2mИCP2m,Z2) Ю
ЮHk-1(CP2mЕCP2m,Z2) Ю Hk-1(CP2m,Z2)ЕHk-1(CP2m,Z2) Ю Hk-1(CP2m,Z2) Ю...Ю H0(CP2m,Z2) = Z2
или
...0 Ю 0 Е 0 Ю 0 Ю Z2 Е Z2 Ю Z2 ЮZ2 Е Z2 Ю Z2 Ю... , т. е. Hk(CP2m,Z2) = Z2 при k< = 2m и Hk(CP2m,Z2) = 0 при k > 2m, что было использовано выше в (9, 10).
Фрактализация гиперкомплексацией порождает в соответствии с (19, 35) следующий цепно гомотопный цепной комплекс расслоения гомологий:
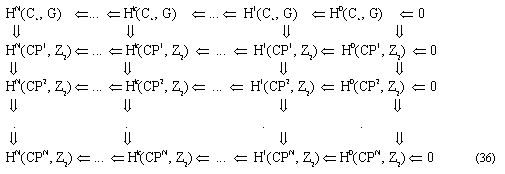
Фрактализация гиперкомплексацией и итерацией индуцирует в соответствии
с (16, 32) сложносоставной цепно гомотопный цепной комплекс:
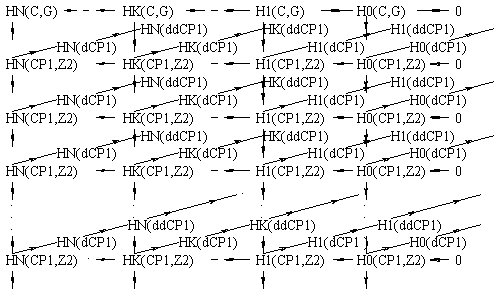
(37)
где в общем случае обозначены ковариантные и контрвариантные функторы гомологий и когомологий базы (по индексу k) и слоя (по индексу m) в виде
Hk(CPm, Z2)
HK(CPM, Z2) Р Hk(CPm, Z2)
HK(CPM, Z2) = б Hk(CPm, Z2)
HK(CPM, Z2) Р Hk(CPm, Z2),
обозначение HK(CPM, Z2) Ю HK(dCPM, Z2) Ю HK(ddCPM, Z2) Ю... вводит в конечных разностях итерации операторов дифференциальных уравнений солитона согласно (20) на каждом шаге гиперкомплексирования. Анализ топологических диаграмм-формул (34 - 37) позволяет построить следующие топологические спектральные последовательности расслоенного поля с когомологией Hk(CPr, Z2) и расслоенной геометрии солитона с когомологией Hm(CPn, Z2), которые в силу теоремы Лере [31] для сингулярных топологий (с кручением) с коэффициенами инцидентности в коммутативном кольце Z2 представляются в виде прямого произведения:
S2k, m = Hk(CPr, Hm(CPn, Z2)) = Hk(CPr, Z2) Д Hm(CPn, Z2),
причём существует изоморфизм симметрии поля и геометрии
H
Электромагнитные солитоны вакуума. Часть 2. «Топологические характеристики электромагнитных солитонов»
R = прS K)+ 2('bb L 'ba) Ы R l c , b a = Kik, pj x
(Rlb — gl bR/2) — (Kik, pj x
i=0е n(-1)i dimHi(CPn, Z2) = (-1)0 1 + (-1)1 1 + (-1)2 2 +... + (-1)2n-1 (n-1) + (-1)2n n = 16 или
i=0е n(-1)i dimHi(CPn, Z2) =1 + n (n + 1) — n2 = 16, откуда n (n + 1) — n2 = 15 или n = 15.
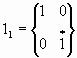 ,
, 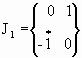 ,
,Z2 = (a1 + a2 Ч i2) + (a3 + a4 Ч i2) Ч i3 = a1 + a2 Ч i2 + a3 Ч i3 + a4 Ч i4 =
= 12Ч (a1 + a2 Ч i2) + J2 Ч (a3 + a4 Ч i2) = 12 Д А1, 2 + J2 Д А3, 4 =
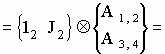
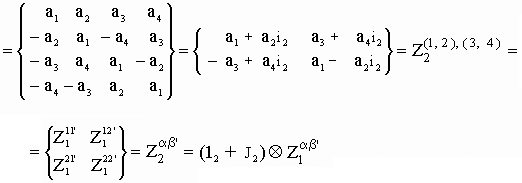
где
dZm
Zm Ь Zm-1
f(f...f(Zn)) = dZm — nЭЭ (1m-1 + Jm-1) Д (1m-2 + Jm-2) Д ...Д (1n-1+Jn-1) = k=n-1Хm-1(1к+Jк)
Zn Ь Zn-1
(1n + Jn) Д (26)
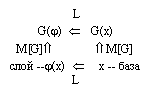 (28)
(28) , (31)
, (31)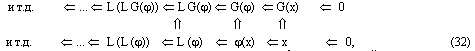
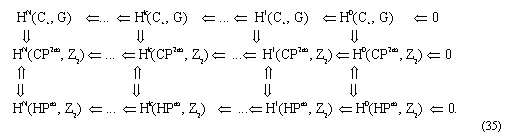
...ЮHk+1(S4m+1,Z2) ЮHk(S4m+1=CP2mИCP2m,Z2) ЮHk(CP2mЗCP2m,Z2) ЮHk(CP2mЕCP2m,Z2) Ю
ЮHk(CP2m,Z2)ЕHk(CP2m,Z2) Ю Hk(CP2m=S4m+1,Z2) ЮHk-1(CP2mИCP2m,Z2) Ю
ЮHk-1(CP2mЕCP2m,Z2) Ю Hk-1(CP2m,Z2)ЕHk-1(CP2m,Z2) Ю Hk-1(CP2m,Z2) Ю...Ю H0(CP2m,Z2) = Z2
или
...0 Ю 0 Е 0 Ю 0 Ю Z2 Е Z2 Ю Z2 ЮZ2 Е Z2 Ю Z2 Ю... , т. е. Hk(CP2m,Z2) = Z2 при k< = 2m и Hk(CP2m,Z2) = 0 при k > 2m, что было использовано выше в (9, 10).