Институт Тринитаризма - Публикации
Брусенцов Н.П.
Логика на шахматной доске
Шахматная доска с математической точки зрения представляет собой дискретную систему декартовых координат. Абсцисса принимает значения a, b, c, d, e, f, g, h, ордината — 1, 2, 3, 4, 5, 6, 7, 8. Каждая пара этих значений, буква—цифра, однозначно указывает одну из 64-х клеток доски. Дискретность обеспечена тем, что фигуры нельзя ставить на границы между клетками.
Эта же по существу конструкция используется в математической логике для представления элементарных логических функций, или операций, также дискретных, отображающих простейшие виды взаимосвязей, посредством которых выражаются всевозможные взаимосвязи вещей и явлений. В отличие от шахматных координат, принимающих количественные, числовые, хотя и не обозначенные в случае абсциссы буквами, значения, логические переменные (термины) и их функции являются качественными характеристиками рассматриваемой ситуации, так что каждая из них либо необходимо (безусловно) удовлетворена, либо необходимо не удовлетворена (антиудовлетворена), либо может удовлетворяться или антиудовлетворяться в зависимости от не фиксируемых определением ситуации условий.
Удовлетворенность обозначают буквами «И» («Истина»), «T» («True») либо цифрой «1», которая в теории вероятностей означает «достоверность», а потому заслуживает предпочтения, по меньшей мере ради унификации. Антиудовлетворенность, обозначаемую буквами «Л» («Ложь»), «F» («False»), ради той же унификации следует представить цифрой «0», символизирующей нулевую вероятность (невозможность). Для промежуточного между «0» и «1» состояния в современной (двухзначной) логике символа нет, поскольку нет и самого этого состояния — оно недопустимо в силу «закона исключенного третьего».
Интерпретируя термины как имена (идентификаторы) качеств, или особенностей, которые могут быть присущи либо антиприсущи характеризуемым посредством них объектам («вещам»), естественно перейти от декартовых координат к декартову произведению совокупностей состояний, принимаемых терминами на различных «вещах». В случае шахматной доски при такой интерпретации имеется два термина — абсцисса и ордината, принимающие состояния, представленные восемью допустимыми для каждого из них значениями. Декартово произведение этих двух множеств значений, т. е. множество попарных сочетаний их, именует 64 клетки доски:
{ a, b,..., h} ? { 1, 2,..., 8} = { a1, a2,...,a8, b1, b2,..., h7, h8}
В логике число независимых (ортогональных) терминов в принципе не ограничено, но число значений, принимаемых термином, в двухзначной логике ограничено двумя: 1 и 0. Поэтому для наглядного представления логической, n-арной в общем случае функции требуется n-мерный куб, а на шахматной доске эффективно представимы только двухместные (двухтерминные) функции, причем достаточно четырехклеточной доски. Например, два термина — x и y, принимающие значения 1 и 0, порождают двухэлементные совокупности состояний { x1, x0}, { y1, y0}, декартовым произведением которых является четырехэлементная совокупность охарактеризованных посредством данных терминов «вещей»:
{ x1, x0} ? { y1, y0} = { x1 y1, x1 y0, x0 y1, x0 y0}
Применительно к конкретному роду «вещей», скажем, к четырехугольникам, термин x может означать прямоугольность, а термин y — равносторонность. В таком случае элементами декартова произведения будут четырехугольники: x1y1 — прямоугольный и равносторонний, т. е. квадрат; x1y0 — прямоугольный, но не равносторонний (неквадратный прямоугольник); x0y1 — непрямоугольный, но равносторонний (неквадратный ромб); x0y0 — непрямоугольный и неравносторонний (не прямоугольник и не ромб).
Пользуясь принятой в современной логике булевой алгеброй, это же декартово произведение можно записать в виде:
{ x, xў } ? { y, yў } = { xy, xyў, xў y, xў yў }
Штрих у термина означает операцию отрицания этого термина — аналог функции, выполняемой в русском языке частицей «не». Например, xў значит не-x. Сочетания терминов xy, xyў,... представляют собой конъюнкции (совмещения) x Щ y, x Щ yў,... символизируемых терминами характеристик.
Заметим, что x1 равносильно x = 1, а x0 равносильно x = 0, или xў = 1, т.е. в отличие от x1 и x0, означающих удовлетворенность и неудовлетворенность критерия x, булевы x и xў означают лишь сами критерии x и не-x. И вообще выражение булевой алгебры, не содержащее знака «= », не представляет определенной взаимосвязи (отношения) входящих в него терминов, а задает только характеристическую функцию, которая служит критерием этой взаимосвязи, принимая при наличии ее значение 1.
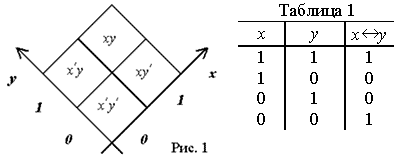Основанное на декартовом принципе координатное (матричное) представление булевых функций ввел Чарлз Пирс в 1885 г. Преимущество такого представления перед обычной таблицей, сопоставляющей значения функции парам значений аргументов, в том, что клетки матрицы как элементы декартова произведения наделены алгебраическими идентификаторами (рис. 1), благодаря чему всякое заполнение их значениями 0 и 1 автоматически порождает булево выражение определяемой данной матрицей функции.
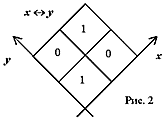Например, функция «эквивалентность» x« y, заданная табл. 1, представляется матрицей (рис. 2), которая отображает подсовокупность { xy, xў yў } рассмотренного выше полного декартова произведения { xy, xyў, xў y, xў yў }. Как видно, подсовокупность { xy, xў yў } получена из полной декартовой совокупности, которой соответствует матрица, содержащая «1» в каждой из четырех клеток, исключением элементов xyў и xў y, т. е. обнулением сопоставленных им клеток матрицы.
В булевой алгебре пирсова матрица трактуется как дизъюнктивная совокупность ее неисключенных элементов, как дизъюнкция их идентификаторов. В случае x« y имеем:
xy Ъ xў yў
где символ дизъюнкции «Ъ » — синоним русского союза «или»: дизъюнкция характеристик удовлетворяется (принимает значение 1), если удовлетворяется хотя бы один из ее членов. Другими словами, дизъюнкция охарактеризованных сочетаниями терминов элементов декартова произведения выражает общую для всех этих элементов особенность, именует составляемый ими класс.
Короче, отображаемые матрицей Пирса совокупности неисключенных элементов декартова произведения интерпретируются в булевой алгебре экстенсионально (объемно), как классы, а не множества представляемых этими элементами вещей. Буль и называл свою алгебру алгеброй классов.
Сами же элементы-вещи охарактеризованы конъюнктивными совокупностями (множествами) терминов, а точнее — подмножествами их полного в данном рассмотрении множества. В булевой алгебре эти подмножества отображаются элементарными конъюнкциями, в которые термины, принадлежащие подмножеству, входят без штрихов, тогда как антипринадлежащие снабжены штрихами. Например, xyў z интерпретируется как { x, z}.
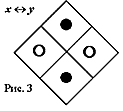Представление булевых функций матрицами Пирса позволяет свести преобразование алгебраических выражений этих функций к элементарным манипуляциям значениями элементов соответствующих матриц, легко перепоручаемым компьютеру. Но сначала адаптируем матрицу к четырехклеточной шахматной доске, заменив цифры 1 и 0 соответственно черной и белой фишками. Теперь представленная на рис. 2 функция x« y отобразится в виде рис. 3. Технически вместо черной и белой фишек удобней черно-белые — с одной из сторон черные, с другой — белые. При этом изменение цвета фишки на противоположный осуществляется ее перевертыванием (инвертированием).
Элементарные операции над представленными посредством доски с черно-белыми фишками булевыми выражениями заключаются (как это нетрудно доказать алгебраически либо перебором существующих возможностей) в следующем.
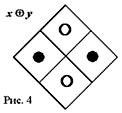Булево отрицание (дополнение) выражения — инвертирование всех представляющих это выражение фишек. Например, инвертирование всех фишек на рис. 3 порождает рис. 4, отображающий функцию xyў Ъ xў y, так называемую исключающую дизъюнкцию: «либо x, либо y, но не оба вместе». В арифметической интерпретации это xЕ y — сложение по модулю два.
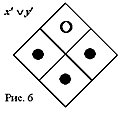
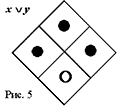Потерминная инверсия выражения (штрихование всех нештрихованных терминов и отмена всех уже имеющихся штрихов) выполняется попарной перестановкой (рокировкой) всех фишек относительно центра матрицы. Например, потерминная инверсия (неисключающей) дизъюнкции x Ъ y (рис. 5) превращает ее в функцию «штрих Шеффера» xў Ъ yў (рис. 6).
Заметим, что функции эквивалентности и исключающей дизъюнкции инвертируются в самих себя, т. е. потерминной инверсией не изменяются.
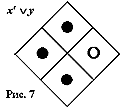
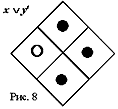
Инверсия всех вхождений одного из терминов осуществляется попарной перестановкой всех фишек вдоль поименованной этим термином оси координат. Так, перестановка на матрице рис. 5 вдоль оси x (либо на рис. 6 вдоль оси y) приводит к положению, изображенному на рис. 7, которым представлена функция материальной импликации x® y, выраженная в совершенной нормальной форме: xy Ъ xў y Ъ xў yў, что равносильно xў Ъ y. Потерминная инверсия ее дает обратную материальную импликацию xе y, т. е. x Ъ yў (рис. 8).
|
|
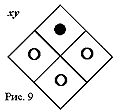
Конъюнкция отображаемых матрицами выражений получается путем теоретико-множественного пересечения представленных этими матрицами совокупностей фишек. Цвет фишки, помещаемой в i-тую клетку матрицы-результата, определяется в зависимости от фишек, находящихся в i-тых клетках пересекаемых матриц. Только если во всех них фишки черные, в i-тую клетку результата помещается черная фишка, а иначе — белая. Короче, i-тая фишка результата будет черной, если она принадлежит каждой из пересекаемых совокупностей. Например, конъюнкция импликаций (x® y)Щ (xе y) формируется пересечением матриц рис. 7 и рис. 8, в результате которого черные фишки сохранятся только в верхней и в нижней клетках, т. е. получится матрица рис. 3, отображающая эквивалентность: x« y. А в результате пересечения трех матриц: рис. 5, рис. 7 и рис. 8, что равносильно пересечению рис. 5 и рис. 3, черная фишка сохранится только в верхней клетке (рис. 9), отображая функцию xy.
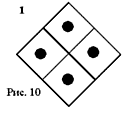
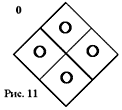
Дизъюнкция булевых выражений реализуется аналогичным образом, но не пересечением, а объединением совокупностей фишек, т. е. для того, чтобы i-тая фишка результата была черной, достаточно даже одной черной i-той фишки в объединяемых совокупностях. Например, дизъюнкция эквивалентности (рис. 3) и импликации (рис. 7) равносильна той же импликации (рис. 7). А дизъюнкция исключающей дизъюнкции (рис. 4) и конъюнкции xy (рис. 9) дает неисключающую дизъюнкцию (рис. 5). Результатом дизъюнкции булевых выражений может быть константа 1, отображаемая матрицей, содержащей во всех клетках черные фишки (рис. 10). Это результат дизъюнкции выражений, например, рис. 3 и рис. 4, или рис. 6 и рис. 9, или любых двух, трех, четырех из рис. 5 — рис. 8. Соответственно конъюнкция выражений рис. 3 и рис. 4 либо рис. 6 и рис. 9 дает в результате константу 0 (рис. 11).
Еще один вид преобразования выражений — «склеивание» смежных различающихся одним термином) конъюнкций. Например:
xy Ъ xyў Ъ xў y є x(y Ъ yў) Ъ (x Ъ xў)y є x Ъ y
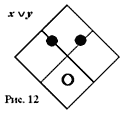
Соответствующая матрица (рис. 5) преобразуется заменой каждой пары расположенных в смежных клетках черных фишек одной черной фишкой, помещаемой на линию, которой эти клетки разделены (рис. 12). Пара xy Ъ xyў превращается в x, пара xy Ъ xў y — в y. Матрица, отображающая выражение в совершенной дизъюнкивной нормальной форме (СДНФ), трансформируется в минимальную ДНФ. Очевидна возможность обратного преобразования путем замены фишек, находящихся на линиях, парами фишек в разделяемых этими линиями клетках.
В сочетании с описанными выше способами матричного отображения булевых функций и фишковой реализации операций инверсии, дополнения, конъюнкции и дизъюнкции над СДНФ-выражениями преобразование СДНФ-матриц в минимализированные и обратно исчерпывающе моделирует булеву алгебру на матрицах Пирса. Подвергаемые алгебраической обработке функции отображаются СДНФ-матрицами, а результаты обработки, получаемые также в СДНФ, могут быть преобразованы в минимальную форму.
Простота алгебры СДНФ-матриц обусловлена тем, что операции дополнения, конъюнкции и дизъюнкции булевых выражений сведены в ней к инверсии, пересечению и объединению совокупностей отмеченных черными фишками клеток. В наибольшей степени простота эта проявляется на примере важнейшей задачи математической логики — решении булевых уравнений.
Джордж Буль (1815—1864) ввел логическое уравнение как аналог числового, в котором значениями чисел могут быть только 1 и 0, причем знак «+» означает неисключающую дизъюнкцию. Таким образом в булевой алгебре, как и в обычной числовой, уравнение — это два выражения, соединенные знаком равенства «= ». Отличие в том, что выражения представляют не числовые, а булевы функции n переменных, называемых терминами и принимающих значения 1, 0. Знак «= » требует равенства значений, принимаемых соединенными им выражениями. Уравнение удовлетворяется на тех наборах значений терминов, на которых значения его левой и правой частей совпадают.
То, что уравнение удовлетворяется не на всех наборах значений терминов (при нетождественности его частей), значит, что оно выражает определенную взаимосвязь терминов — отношение, устанавливающее допустимое значение каждого термина в зависимости от значений других терминов удовлетворяющей уравнению n-ки. Решение булева уравнения относительно одного из входящих в него терминов заключается в определении этого термина как функции всех рассматриваемых терминов.
|
Короче, решаемое уравнение тождественно преобразуется к виду, при котором искомый термин составляет одну из его частей.
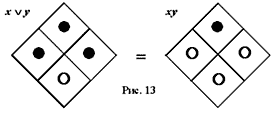
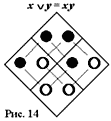
На языке матриц Пирса булево уравнение представляется парой матриц, соединенных знаком «= » (рис. 13), либо двойной матрицей, содержащей в каждой клетке по две фишки: в левом углу относящаяся к левой части уравнения, в правом углу относящаяся к правой части (рис. 14).
Тождественное преобразование отображающей булево уравнение двойной матрицы, т. е. придание уравнению требуемого вида, осуществляется попарной инверсией фишек в отдельных клетках матрицы. Инверсия обеих находящихся в одной и той же клетке фишек не меняет статуса клетки: если фишки одинаковы, то и после инверсии будут одинаковыми, а если различны, то останутся различными — удовлетворенность/неудовлетворенность уравнения n-кой терминов, сопоставленной этой клетке, сохраняется.
На рис. 15 показаны три тождественные разновидности уравнения x Ъ y = xy. Первая представляет собой решение данного уравнения относительно термина y.
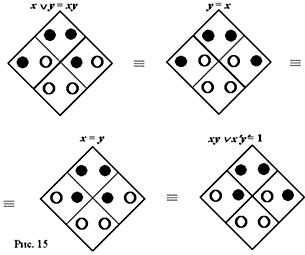Получена она инверсией фишек в правой клетке матрицы, в результате чего левой частью уравнения стал искомый термин y, а правая часть превратилась в термин x. Вторая разновидность - решение относительно термина x, достигнутое инверсией левой клетки. Третья разновидность - так называемая единичная форма данного уравнения: xy Ъ xў yў = 1, при которой правая часть его равна 1, а левая часть представляет собой характеристическую функцию отображаемого уравнением отношения, т. е. функцию, принимающую значение 1, когда это отношение имеет место. Значение 1 в правой части (четверка черных фишек) получено инверсией фишек во всех клетках, кроме верхней.
Другой пример: отношение, характеристическая функция которого — материальная импликация xў Ъ y (рис. 7). Матрица соответствующего уравнения и матрицы его решений относительно консеквента y и антецедента x показаны на рис. 16.
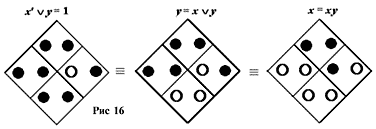Термины взаимосвязаны рекурсивной (нечеткой) зависимостью: y = x Ъ y означает, что если x = 1 (x дано), то y = 1, т. е. с необходимостью дано и y, а если x = 0 (x исключено), то y = y, т. е. значение y не фиксировано, произвольно. С другой стороны, x = xy означает, что если y = 0 (y исключено), то и x исключено, т. е. x = 0, а если y = 1 (y дано), то x = x, т. е. значение x произвольно. Оба термина, как x, так и y, предполагаются необходимо переменными, иначе возникнут так называемые парадоксы материальной импликации: «если x противоречиво, то оно влечет всякое y», «общезначимое y следует из всякого x». Но ясно, что в этих случаях ни импликации, ни какой-либо другой взаимосвязи между терминами нет: один из них оказывается константой, а другой волен принимать значения независимо от него, сам по себе.
Такое же истолкование материальной импликации можно извлечь и непосредственно из матрицы рис. 7, рассматривая ее как график функции y = f(x) в дискретных декартовых координатах (рис. 1) и как график обратной функции x = g(y) в тех же координатах, т. е. глядя на рис. 7 соответственно справа вверх и слева вверх. Функция y = f(x) при x = 1 определена однозначно: y = 1, а при x = 0 неоднозначна: значением y может быть как 1, так и 0. Функция x = g(y) однозначна при y = 0 и неоднозначна при y = 0.
Наиболее содержательное («вещественное») истолкование рассматриваемой матрицы заключается в том, что она представляет собой совокупность отмеченных черными фишками вещей xy, xў y, xў yў, которая содержит по одной x- и y-вещи и по две xў — и y-вещи. Поэтому x-вещь, т. е. xy, непременно есть y, и yў -вещь, т. е. xў yў, не может не быть xў, тогда как xў — и y-вещи неоднозначны: xў — это xў y либо xў yў, а y — это xy либо xў y.
В случае n-терминных функций, n > 2, матрица Пирса трансформируется в n-мерный куб, однако его отображают на 2n-клеточную шахматную доску в форме «карты Карно».
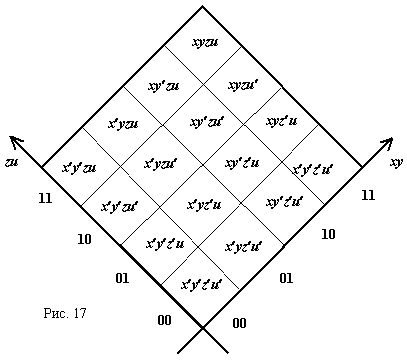На рис. 17 представлена четырехтерминная доска этого рода. Обычная 64-клеточная шахматная доска достаточна для отображения 6-терминных функций, но непосредственное манипулирование ими в таком представлении непосильно человеку. Вместе с тем это наредкость благодатная сфера применения компьютера.
Брусенцов Н.П. Логика на шахматной доске // «Академия Тринитаризма», М., Эл № 77-6567, публ.11484, 07.09.2004
[Обсуждение на форуме «Наука»]
