Всё бесконечное множество натуральных чисел N образовано членами пяти арифметических прогрессий, имеющих следующий вид

N_n= А + В× (n–1) = В× n + А – В ,        (1)

где А – это первое число (первый член) прогрессии; В – шаг (разность) прогрессии; n=1, 2, 3, … – порядковый номер натурального числа внутри данной прогрессии. Каждую из пяти арифметических прогрессий мы будем называть классом чисел и обозначать его как класс АВ (первый член и разность прогрессии). Нетрудно убедиться, что все натуральные числа разделяются на следующие пять классов: 14, 26, 34, 46, 66. В табл. 1 приведено по 24 первых натуральных числа N из каждого класса (в пяти столбцах). Пять чисел N, расположенных в строке табл. 1 (по одному из каждого класса), будем называть n-м слоем натуральных чисел.

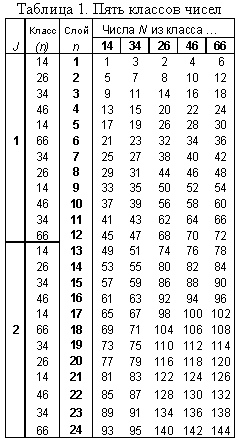
Классы чисел в натуральном ряду чередуются определенным образом – начиная с единицы, бесконечное количество раз повторяется набор из двенадцати классов, которые мы назовем дюжиной классов: 14, 26, 34, 46, 14, 66, 34, 26, 14, 46, 34, 66. Поскольку номера слоев (n) в табл. 1– это суть натуральный ряд (уходящий вниз до бесконечности), то слева от него указан класс (АВ) для каждого числа n, а также порядковые номера дюжин (J=1, 2, …), образованных этими классами. Таким образом, в каждой дюжине по три числа из классов 14 и 34, а доля каждого из этих классов составляет Dº 3/12=1/4, т. е. по 25% (как внутри дюжины, так и среди всех натуральных чисел). Ещё в каждой дюжине по два числа из классов 26, 46 и 66, а доля каждого из них составляет Dº 2/12=1/6, т. е. около 16,67…% (как внутри дюжины, так и среди всех натуральных чисел). Иначе говоря, на любом достаточно большом отрезке натурального ряда вероятность встречи с числами из классов 14 или 34 составляет по 25%, а с числами из классов 26, 46, 66 – примерно по 16,7%.

Чтобы определить, к какому классу принадлежит произвольное натуральное число N достаточно разделить это число на 12 и посмотреть чему равен остаток. Например, у числа N=19 остаток от деления на 12 равен 7, значит наше число N из класса 34, поскольку 7-ому числу в первой дюжине (по порядку от её начала, см. табл.1 ) соответствует именно 34 класс. Если остаток от деления некого числа N на 12 окажется равным 0 (нулю), то число N будет из класса 66 (это единственный класс, в котором числа N³ 12 делятся нацело на 12).

Очевидно, что в классах 26, 46, 66 – только четные числа, а все простые числа содержатся исключительно в классах 14 и 34. Причем в самом начале натурального ряда простых чисел в классе 34 больше, нежели в классе 14, но на бесконечности этот «сдвиг» исчезает. Так, если на некотором отрезке (с началом в единице) количество простых чисел равно Р, а количество простых чисел в классе 14 равно Р₁₄, то имеет место такое соотношение:

Р₁₄/P ³ (2 + F*/P^m) ^-1,           (2)

где F*³ 4 (возможно, F* – это число Фейгенбаума?); m=е^-0.5» 0,6065. С увеличением отрезка отношение Р₁₄/P растет от 0,3 до 0,5. Например, при K=352000 имеем k/K» 0,4996, т. е. в классе 14 будет не менее 49,96% всех простых чисел (уже почти половина всех простых чисел).

Пусть n* – это порядковый номер первого числа из данного класса в J-й дюжине (в каждой дюжине только одному номеру n мы присваиваем «звездочку»). Например, во второй дюжине (J=2, см. табл. 1) для 14 класса имеем n*=4, поскольку в первой дюжине (J=1) уже были три числа из класса 14 (были n*=1; n=2; n=3). Ясно, что в третьей дюжине (J=3) в классе 14 будем иметь n*=7, т. к. во второй дюжине ещё «содержатся» n=5 и n=6. Таким образом, для класса 14 (как и для класса 34) получим арифметическую прогрессию 1, 4, 7, 10, …, иначе говоря, n*=1+3× (J–1)= 3× J–2, где J=1, 2, 3, …. Совершенно аналогично для классов 26, 46 и 66 мы получим арифметическую прогрессию 1, 3, 5, 7, …, или n*=1+2× (J–1)= 2× J–1. Таким образом,

n* = 1+K× (J–1) = K× J–K+1 ,           (3)

где K – это количество чисел данного класса в дюжине (см. табл. 2).

Пусть S* – это сумма всех натуральных чисел N из данного класса внутри J-й дюжины. Например, для 14 класса в первой дюжине (J=1, см. табл. 1) имеем S*=1+5+9=15, а во второй дюжине (J=2) имеем S*=13+17+21=51. Нетрудно также получить формулу, связывающую n* и S*:

S* = g× n* + h , (4)

где значения числовых коэффициентов g и h следует брать из табл.2, причем g=K× B, а h=K× A – для классов 14, 34, и h=K× (A–B)+B – для классов 26, 46, 66. Если формулу (3) подставить в формулу (4), то получим

S* = G× J – H ,                (5)

где значения числовых коэффициентов G и H следует брать из табл.2, причем G=K²× B, а H=K× (B+A)–K²× B – для классов 14, 34, и H=K× A+B–K²× B – для классов 26, 46, 66.

Если в любой J-й дюжине найти общую сумму всех натуральных чисел, суммируя формулы (5) для всех пяти классов, то получим выражение

S S* = 144× J – 66 .             (6)

Поэтому при J® ¥ можно утверждать, что S*/S S* ® G/144=D (см. табл.2), т. е. справедлив следующий довольно интересный и далеко неочевидный вывод: сумма чисел (S*) данного класса (АВ) в любой дюжине составляет такую же долю (D) от суммы всех чисел дюжины (S S*), как и их количество (см. вывод значений для D в начале главы).

Пусть S – это сумма всех натуральных чисел N из данного класса во всех дюжинах (до J-й включительно). Например, для 14 класса во второй дюжине (J=2, см. табл. 1) будем иметь S=15+51=66. Нетрудно получить формулу

S = W× J² + Z× J ,       (7)

где значения числовых коэффициетов W и Z следует брать из табл.2, причем W=1,5× K× B и Z=K× (A–B/2) – для классов 14, 34; W=K× B и Z=K× A–K× B+B – для классов 26, 46, 66.

Если для любого количества дюжин (J) найти общую сумму всех натуральных чисел, суммируя формулы (7) для всех пяти классов, то получим

S S = 72× J ²+ 6× J . (8)

Но этому же равна и сумма 1+2+3+…+12× J, которая выражает сумму всех натуральных чисел от N=1 до N=12× J. Именно равенство двух указанных сумм доказывает, что понятие о пяти классах и дюжине справедливо (“работает”) для всего бесконечного ряда натуральных чисел. Кроме того, при J® ¥ из формулы (8) вытекает, что S/S S® W/72=D (см. табл.2), т. е. справедлив также интересный и совсем уже неочевидный, вывод: сумма чисел (S) данного класса (АВ) во всех дюжинах (до J-й включительно) составляет такую же долю (D) от суммы всех чисел (S S), как и их количество (K, см. вывод значений для D в начале главы). 

Выше мы договорились, что пять натуральных чисел N₁₄,  N₂₆,  N₃₄,  N₄₆,  N₆₆  (по одному из каждого класса) будем называть n-ым слоем. Например, при n=1 имеем 1-й слой чисел: 1, 2, 3, 4, 6; при n=2 имеем 2-й слой: 5, 8, 7, 10, 12 и т. д. Тогда для любого n-го слоя справедливы соотношения:

N₃₄– N₁₄= 2;   N₄₆– N₂₆= 2;   N₆₆– N₂₆= 4;   N₂₆/N₁₄ » 3/2+0,125/n        (9)

Каждый слой (т. е. при n=1, 2, 3, …) можно характеризовать средним значением. Так, среднее арифметическое каждого слоя будет равно

Na º (N₁₄+ N₂₆+ N₃₄+ N₄₆+ N₆₆)/5 = 5,2× n ,            (10)

Ng º (N₁₄× N₂₆× N₃₄× N₄₆× N₆₆)^1/5 = 5,1017× n ,            (11)

где 5,1017 – это среднее геометрическое набора из пяти шагов В.

Среднее гармоническое каждого слоя будет равно

Nh º 5/(1/N₁₄+1/N₂₆+1/N₃₄+1/N₄₆+1/N₆₆) = 5× n ,                            (12)

Ns º [(N₁₄²+N₂₆²+N₃₄²+N₄₆²+N₆₆²)/5] ^½= 5,2 915× n ,         (13)

где 5,2915 – это квадратичное среднее набора из пяти шагов В.

Степенное среднее каждого слоя будет равно

Np º [(N₁₄^p+N₂₆^p+N₃₄^p+N₄₆^p+N₆₆^p)/5]^1/p = Q× n ,                           (14)

где Q – это степенное среднее набора из пяти шагов В; р¹ 0 – любое число, причем как частные случае получаем: при р=1 – среднее арифметическое; при р=2 – квадратичное среднее; при р® 0 степенное среднее стремится к среднему геометрическому. Чем больше показатель степени р, тем ближе степенное среднее Np к числу N₆₆ (в каждом слое). Чем меньше показатель степени р, тем ближе степенное среднее Np к числу N₁₄, а при р=–1 получаем среднее гармоническое, которое расположено посередине между числами N₆₆ и N₁₄ (действительно, самое гармоничное расположение). Для всех средних погрешность можно оценить формулой вида: abs(ОП)» Z× n^-z, например, для среднего гармонического имеем Z=lge» 0,4343; z=1, т. е. в каждом новом слое модуль относительной погрешности быстро убывает.