Утверждается, что главное понятие философии Канта – понятие синтеза. Излагаются основы т.н. Проективно Модальной Онтологии как формальной аксиоматической теории синтеза и делается маленькое приложение этой теории к конструкции синтетических суждений у Канта

Центральным понятием философии Канта является понятие «синтеза». В основании теоретического разума, согласно Канту, лежит фундаментальная способность синтеза – трансцендентальная апперцепция. Развитие разума во всех сферах осуществляется в постоянном восхождении от разного рода сторон и аспектов синтеза к синтетическим целостностям. Таков синтез восприятий на основе априорных схем пространства и времени в чувствительности, синтез понятий на основе категорий, способность априорных синтетических суждений, итоговые синтезы теоретического разума в идеях Мира, Души и Бога, синтезы нравственные и эстетические в априорных формах нетеоретических видов разума, и т.д. В связи с этим логическая реконструкция идей Канта может получить свое выражение только в рамках некоторой «логики синтеза», средствами которой будет выразимо понятие синтеза и разного рода синтетические процедуры. В работах автора (V.Moiseev. Projectively Modal Ontology // Logical Studies, № 9, 2002. – (http://www.logic.ru/LogStud/09/LS9.html); Wiaczeslaw I. Moisiejew. Ontologia Stanisława Leśniewskiego i Logika Wszechejedności // Kwartalnik Filozoficzny. Tom XXXII. Zeszyt 1. Przeł. Paweł Rojek. Krakуw. Polska Akademia Umiejętności, Uniwersytet Jagielloński. 2004. – pp.101-126.; Моисеев В.И. К аксиоматике Модальной Онтологии // Рационализм и культура на пороге 3-го тысячелетия: материалы 3-го Российского Философского конгресса (16 – 20 сентября 2002 г.). В 3-х тт. Том 1. Философия и методология науки, эпистемология, логика, философия природы, философия сознания, философия техники, философия образования. Ростов н/Д; Изд-во СКНЦ ВШ, 2002. – С. 283-284; Моисеев В.И. Теория ментальных многообразий как аксиоматическая система // Логика Добра. – М.: Эдиториал УРСС, 2004. – С. 295-300) развивается версия философской логики, так называемая Проективно Модальная Онтология, средствами которой можно дать конструктуивное определение двойственных операторов анализа и синтеза. Речь идет о логической системе, выстраиваемой в стиле Онтологии и Мереологии Станислава Лесьневского, но использующей в качестве первичного предиката некоторый 7-местный предикат Mod(a,b,c,f,e,h, a) – «в контексте a a есть аспект начала b при условии c и отображении f, и b есть полнота аспекта a при условии e и отображении h». Средствами этой системы можно дать корректное определение операторов анализа и синтеза, начав строить некоторое логическое исчисление, своего рода «логику синтеза», в рамках которой можно надеяться на более адекватное воспроизведение логико-философских идей кантовской системы. Ниже предполагается дать краткий обзор этой логической системы и рассмотреть примеры реконструкции и новых интерпретаций ряда синтетических концептов философии Канта в рамках данной системы.

1. 7a -Онтология

В рамках Проективно Модальной Онтологии Прототетика Лесьневского используется без всяких изменений, затем, за исключением предиката e, принимается синтаксис построения выражений Онтологии в форме различных категориальных типов, правила логического вывода (Slupecki J. S.Lesniewski’s Calculus of Names. Studia Logica, V.3., 1955. – pp.21-27), кроме правила экстенсиональности. Прототетические определения используются без изменений. Онтологические определения также претерпевают существенные изменения (подробнее см. Moiseev V. Projectively Modal Ontology // Logical Studies, № 9, 2002. – http://www.logic.ru/LogStud/09/LS9.html). Как и у Лесьневского, определения добавляются как теоремы системы.

Основная идея построения новой аксиоматики состоит в использовании некоторого семиместного предиката Mod вместо предиката «e » Лесьневского.

Идея такого предиката предполагает следующую онтологию. Определены некоторые источники – генераторы — бытия (модусы), они способны образовывать свои аспекты (моды) в рамках некоторых ограничивающих условий (моделей), которые накладываются на модусы и ограничивают их до мод. Сама процедура ограничения может быть названа проектором. В общем случае проектор — это двуместная операция, определенная на модусе и модели, и образующая в результате моду этого модуса в этой модели. В то же время на отношение моды и модуса можно посмотреть и с другой стороны. Можно представить, что не мода образуется из модуса, но наоборот, модус из моды. В этом случае нужно не начало ограничения, но некоторое начало расширения моды до модуса. Такое начало я буду называть модулем. Процедуру расширения моды до модуса на основе некоторого модуля также можно рассматривать как некоторый двуместный функтор, который я буду называть сюръектором. Определяясь на моде и модуле, сюръектор дает модус этой моды в этом модуле. В целом, получаем симметричную схему такого вида:

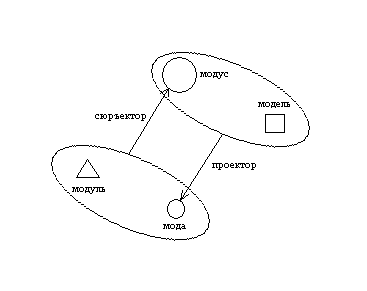
Предикат Mod должен выразить указанную координацию всех шести элементов – модуса, моды, модели, модуля, проектора и сюръектора. Следовательно, он должен быть, как минимум, шестиместным предикатом. Кроме того, следует учесть, что возможны разные контексты определения всех указанных объектов. Например, в одном контексте объекты a и b могут быть таковы, что b – мода a, в другом контексте, наоборот, a может быть модой b. Чтобы выразить такую зависимость всех модальных определений от некоторых контекстов, я введу седьмой элемент, который назову спецификатором. Спецификатор задает конкретный контекст, в рамках которого определены все указанные шесть объектов. Теперь предикат Mod становится семиместным предикатом, и его можно записать в следующем виде:

Mod(a,b,c,f,d,h, a) – «в контексте a a есть мода модуса b в модели c и с проектором f, и b есть модус моды a в модуле d с сюръектором h»

Развиваемую систему я буду называть Проективно-модальной 7a -Онтологией, или просто 7a -Онтологией.

Первая аксиома 7a -Онтологии:

(АО1) Moda(a,b,a) є Modus(a,a) Щ " d(Moda(b,d,a) Й Moda(a,d,a)) Щ Moda(b,b,a)

Здесь:

Modus(a,a) є $ b$ c$ f$ d$ hMod(b,a,c,f,d,h,a) – «а есть a -модус»

Moda(a,b,a) є $ c$ f$ d$ hMod(a,b,c,f,d,h,a) – «а есть a -мода модуса b»

В этой первой аксиоме определяются свойства отношения «быть модой модуса в контексте a » (Modа(…,…,a)). Требуется, чтобы это отношение было транзитивным и рефлексивным, чтобы всякая мода одновременно была и модусом.

Вторая аксиома:

(АО2) Mod(a,b,c,f,d,h,a) є (a =^a1 f(b,c)) Щ (b =^a2 h(a,c)) Щ $ хMod(x,b,c,f,d,h,a) Щ $ yMod(a,y,c,f,d,h,a),

где (x =^a1 y) є " b" с" f" d" h(Mod(x,b,c,f,d,h,a) є Mod(y,b,c,f,d,h,a))Щ Moda(x,a) Щ Moda(y,a) – равенство мод по всем остальным объектам (кроме спецификатора),

Moda(a,a) – это формула $ b$ с$ f$ d$ hMod(a,b,c,f,d,h,a), и читается она как «a есть a -мода».

(x =^a2 y) є " a" с" f" d" h(Mod(a,x,c,f,d,h,a) є Mod(a,y,c,f,d,h,a))Щ Modus(x,a) Щ Modus(y,a) – равенство модусов по всем остальным объектам (кроме спецификатора)

В этой аксиоме выражается связь функторов f и h с предикатом Mod

С использованием указанных аксиом в рамках некоторой подходящей логической системы можно строить аксиоматическую теорию предиката Mod. В работах (Moiseev V. Projectively Modal Ontology // Logical Studies, № 9, 2002. – (http://www.logic.ru/LogStud/09/LS9.html); Моисеев В.И. К аксиоматике Модальной Онтологии // Рационализм и культура на пороге 3-го тысячелетия: материалы 3-го Российского Философского конгресса (16 – 20 сентября 2002 г.). В 3-х тт. Том 1. Философия и методология науки, эпистемология, логика, философия природы, философия сознания, философия техники, философия образования. Ростов н/Д; Изд-во СКНЦ ВШ, 2002. – С. 283-284) я развивал версию Онтологии с использованием в качестве первичного четырехместного предиката Mod(a,b,c,f), который можно было бы определить в терминах 7a -Онтологии через формулу $ d$ hMod(a,b,c,f,d,h,a).

Cимволом Mod^k1…km7(x_k1,…,x_km, a) я буду передавать случай формулы с предикатом Mod, в которой свободными остаются спецификатор a и только переменные x_k1,…,x_km, стоящие на местах под номерами k₁ <…< k_m Ј 6, в то время как остальные переменные связаны кванторами сущестования. Например, Mod¹²³⁷(a,b,c,a) є $ f$ d$ h Mod(a,b,c,f,d,h,a).

Под равенством (a =a b) будет иметься в виду конъюнкция Mod¹²⁷(a,b,a)Щ Mod¹²⁷(b,a,a).

2. Теория множеств в 7a -Онтологии

Пусть P — функтор категориального типа S/а, где а – некоторый категориальный тип. Рассмотрим определение

DSET(D,а)1. x О <P> є D (x) Щ P(x)

Здесь D (x) есть некоторое условие на х, не являющееся теоремой 7a -Онтологии. В определении DSET(D,а)1 вводится некоторый функтор F[P] с параметром Р и категориальным типом S/(а,S/а), т.e. F[P](x) есть xО <P>. Я буду использовать символику «О <P>» для выражения функтора F[P], т.e. О <P>(x) есть xО <P> в данном случае. Символ «О » представляет из себя при этом только лишь часть обозначения указанного функтора без какого-либо самостоятельного смысла, но неформально читать выражение «x О <P>» можно обычным способом: «х принадлежит множеству <P>». Таким образом, определение DSET(D,а)1 представляет из себя прототетическое определение в 7a -Онтологии. Спецификацию (D,а) можно называть сортом «множества». Используя определение DSET(D,а)1, можно развить в 7a -Онтологии свою версию теории множеств. Например, можно использовать определения:

DSET(D,а)2. x О (<P>И <Q>) є D (x) Щ (P(x) Ъ Q(x))

DSET(D,а)3. x О (<P>З <Q>) є D (x) Щ (P(x) Щ Q(x))

DSET(D,а)4. x О <P>ў є D (x) Щ Щ P(x)

DSET(D,а)5. <P> =_z <Q> є " x(x О <P> є xО <Q>)

DSET(D,а)6. x О {a} є D (x) Щ (x =a a)

3. Логика анализа и синтеза

Пусть дана версия 7a -Онтологии с двумя фиксированными функторами – проектором Ї и сюръектором ­. В такой Онтологии в формуле Mod(a,b,c,Ї,d,­,a) будут варьировать только 4 переменных a,b,c и d, так что реально мы имеем дело с некоторой 5a -Онтологией. В силу фиксации проектора и сюръектора, можно эту версию Онтологии обозначать как «5Ї ­ a -Онтология».

В 5Ї ­ a -Онтологии можно использовать следующие онтологические определения:

Dd1. Mod¹²⁴⁶⁷(x,d_c(b),Ї,­,a) є $ y(Mod¹²³⁴⁶⁷(y,b,c,Ї,­,a) Щ Mod¹²⁴⁶⁷(x,y,Ї,­,a)) – модусно-модальное определение дифференциала d_c с параметром с (с-дифференциала)

Dd2. Mod¹²⁴⁶⁷(d_c(b),х,Ї,­,a) є $ y(Mod¹²³⁴⁶⁷(y,b,c,Ї,­,a) Щ Mod¹²⁴⁶⁷(y,х,Ї,­,a)) – модально-модусное определение дифференциала d_c с параметром с (с-дифференциала)

Di1. Mod¹²⁴⁶⁷(i_e(a),х,Ї,­,a) є $ y(Mod¹²⁴⁵⁶⁷(а,y,Ї,e,­,a) Щ Mod¹²⁴⁶⁷(у,х,Ї,­,a)) – модально-модусное определение интеграла i_e с параметром е (е-интеграла)

Di2. Mod¹²⁴⁶⁷(х,i_e(a),Ї,­,a) є $ y(Mod¹²⁴⁵⁶⁷(а,y,Ї,e,­,a) Щ Mod¹²⁴⁶⁷(х,у,Ї,­,a)) – модусно-модальное определение интеграла i_e с параметром е (е-интеграла)

На основе этих определений может быть развито своего рода исчисление (логических) дифференциалов и интегралов. Далее в этом параграфе я буду сокращать формулу Mod(a,b,c,Ї,e,­,a) через формулу Mod(a,b,c,e), оставляя в явной записи только варьирующие элементы. Для формулы Mod(a,b,c,e) также можно использовать нотацию, принятую в 7a -Онтологии, только опуская индексы 4, 6 и 7. Например, выражение Mod¹²⁴⁵⁶⁷(a,b,Ї,e,­,a) будет выглядеть как выражение Mod¹²⁵(a,b,e), и т.д. Под записью b e a будет иметься в виду в этом случае формула Mod¹²⁴⁶⁷(a,b,Ї,­,a). Могут быть доказаны, например, следующие теоремы.

Теорема 1. Mod(a,b,c,e) Й (d_c(b) = а)

Теорема 2. Mod(a,b,c,e) Й (i_e(a) = b)

Теорема 3. Mod(a,b,c,e) Й (i_e(d_c(b)) = b)

Теорема 4. Mod(a,b,c,e) є (d_c(b) = а)Щ (i_e(a) = b)

Аналогично могут быть доказаны следующие теоремы.

Теорема 5. Mod(a,b,c,e) Й (i_e(a) = b)

Теорема 6. Mod(a,b,c,e) Й (i_e(d_c(b)) = b)

Теорема 7. Mod(a,b,c,e) Й (d_c(i_e(а)) = а)

Далее выражения i_e(d_c(b)) и d_c(i_e(а)) я буду обозначать также в форме i_e° d_c(b) и d_c° i_e(а) соотв.

Теорема 8. (d_c(b) = а)Щ (i_e(a) = b) Й Mod(a,b,c,e)

Теорема 9. Mod(a,b,c,e) є (d_c(b) = а)Щ (i_e(a) = b)

Рассмотрим определение новых операторов.

D1D. Mod¹²⁴⁶⁷(x,D _ec(a),Ї,­,a) є $ y$ z(Mod¹²⁴⁵⁶⁷(a,y,Ї,e,­,a) Щ Mod¹²³⁴⁶⁷(z,y,c,Ї,­,a) Щ Mod¹²⁴⁶⁷(x,z,Ї,­,a)) – модусно-модальное определение оператора D _ec

D2D. Mod¹²⁴⁶⁷(D _ec(a),х,Ї,­,a) є $ y$ z(Mod¹²⁴⁵⁶⁷(a,y,Ї,e,­,a) Щ Mod¹²³⁴⁶⁷(z,y,c,Ї,­,a) Щ Mod¹²⁴⁶⁷(z,х,Ї,­,a)) – модально-модусное определение оператора D _ec

D1С. Mod¹²⁴⁶⁷(x,С _cе(a),Ї,­,a) є $ y$ z(Mod¹²³⁴⁶⁷(у,а,с,Ї,­,a) Щ Mod¹²⁴⁵⁶⁷(у,z,Ї,e,­,a) Щ Mod¹²⁴⁶⁷(x,z,Ї,­,a)) – модусно-модальное определение оператора С _cе

D2С. Mod¹²⁴⁶⁷(С _cе(a),х,Ї,­,a) є $ y$ z(Mod¹²³⁴⁶⁷(у,а,с,Ї,­,a) Щ Mod¹²⁴⁵⁶⁷(у,z,Ї,e,­,a) Щ Mod¹²⁴⁶⁷(z,х,Ї,­,a)) – модально-модусное определение оператора С _cе

Теорема 10. Modus(a) Щ Model(c) Щ Modul(e) Й (D _ec(a) = d_c° i_e(а))

Теорема 11. Modus(a) Щ Model(c) Щ Modul(e) Й (С _cе(a) = i_e° d_c(а))

Оператор D _ec можно также называть ес-интегродифференциалом, а оператор С _cе – се-диффероинтегралом. Оба оператора «сдвигают» модус до другого модуса, но интегродифференциал осуществляет этот сдвиг, сначала расширяя модус до его интеграла, затем сужая этот интеграл в каком-то дифференциале. Диффероинтеграл, наоборот, сначала сужает модус до какого-то дифференциала, затем расширяя этот дифференциал до некоторого его интеграла. Модель с и модуль е конкретизируют, до каких именно дифференциалов и интегралов идут сужения и расширения.

Операторы D _ec и С _cе — примеры композиционных операторов, полученных как композиции интегралов и дифференциалов. В общем случае можно предполагать наличие целого семейства подобных композиционных операторов.

Далее могут быть определены операторы анализа и синтеза.

Оператор анализа А должен воздействовать на модус и давать в результате некоторое множество его мод. Для полного определения такого оператора необходимо уточнить, какие используются проекторы и модели. Поскольку результатом оператора анализа будет именно множество, то необходимо будет воспользоваться представленной выше методологией работы с множествами.

DA. a О A[b,c₁,…,c_n,Ї ₁,…,Ї _n] є Mod¹²³⁴⁷(a,b,c₁,Ї ₁,a)Ъ … Ъ Mod¹²³⁴⁷(a,b,c_n,Ї _n,a)

Здесь множество A[b,c₁,…,c_n,Ї ₁,…,Ї _n] может быть прочитано как «множество мод модуса b, полученных в моделях c₁,…,c_n с проекторами Ї ₁,…,Ї _n соотв.». Символ «А» обозначает оператор анализа.

Наоборот, оператор синтеза S должен действовать на множество мод, сопоставляя им некоторый их модус. Чтобы избежать неоднозначности, нужно будет указать, какие именно здесь используются модули и сюръекторы. В итоге получим:

DS1. S[{a₁,…,a_n},e₁,…,e_n, ­ ₁,…,­ _n] a e x є $ y(Mod¹²⁵⁶⁷(a₁,y,e₁, ­ ₁,a)Щ …Щ Mod¹²⁵⁶⁷(a_n,y,e_n,­ _n,a) Щ (y a e x)) – модусно-модальное определение оператора синтеза

DS2. x a e S[{a₁,…,a_n},e₁,…,e_n, ­ ₁,…,­ _n] є $ y(Mod¹²⁵⁶⁷(a₁,y,e₁, ­ ₁,a)Щ …Щ Mod¹²⁵⁶⁷(a_n,y,e_n,­ _n,a) Щ (x a e y)) – модально-модусное определение оператора синтеза

Здесь использовано выражение {a₁,…,a_n}, которое может быть определено следующим образом:

х О {a₁,…,a_n} є (x =a_a1)Ъ …Ъ (x =a _an)

и представляет из себя «множество», до a -точности состоящее из a -модусов a₁,…,a_n.

Хотя такого рода определение не совпадает по форме с определением х О <P> є D (x)Щ P(x), но его можно рассматривать как сокращение для определения

х О <(x =a a₁)Ъ …Ъ (x =a a_n)> є Modus(x,a) Щ ((x =a a₁)Ъ …Ъ (x =a a_n))

Многоточие «…» относится к метаязыку, так что в объектном языке всегда предполагается конкретное конечное число элементов (x =a a₁),…, (x =a a_n).

Пусть элементы a_i, b, c_i, Ї _i, e_i и ­ _i связаны соотношением Mod(a_i,b,c_i,Ї _i,e_i,­ _i,a) для каждого i=1,…,n. Можно доказать следующие теоремы.

AS-Теорема. Mod(a₁,b,c₁,Ї ₁,e₁,­ ₁,a)Щ …Щ Mod(a_n,b,c_n,Ї _n,e_n,­ _n,a) Й A[S[{a₁,…,a_n},e₁,…,e_n, ­ ₁,…,­ _n],c₁,…,c_n,Ї ₁,…,Ї _n] {a₁,…,a_n}

SA-Теорема. Mod(a₁,b,c₁,Ї ₁,e₁,­ ₁,a)Щ …Щ Mod(a_n,b,c_n,Ї _n,e_n,­ _n,a) Й S[A[b,c₁,…,c_n,Ї ₁,…,Ї _n],e₁,…,e_n,­ ₁,…,­ _n] =a ²₁ b

Теорема 12. b =a S[{a₁,…,a_n},e₁,…,e_n, ­ ₁,…,­ _n] є (b =a i_e1(a₁))Щ …Щ (b =a i_en(a_n)),

где интегралы i_e1,…, i_en определены на основе сюръекторов ­ ₁,…,­ _n соотв.

Теорема 13. {a₁,…,a_n} =_z A[b,c₁,…,c_n,Ї ₁,…,Ї _n] є (a₁ =a d_c1(b))Щ …Щ (a_n =a d_cn(b)),

где дифференциалы d_c1,…, d_cn определены на основе проекторов Ї ₁,…,Ї _n соотв.

4. Пример из философии Канта

На основе приведенных выше конструкций – логических дифференциалов, интегралов, интегродифференциалов, операторов анализа и синтеза – можно строить достаточно богатую логическую систему, которую можно пытаться интерпретировать на различных моделях, в том числе и на материале философии Канта. Приведу здесь лишь один пример, предполагая, что систематическая реконструкция философской логики Канта – задача отдельного и основательного исследования.

Синтетические суждения. По мысли Канта, синтетическое суждение расширяет тот смысл, который предполагается определением субъекта. Если S – субъект суждения, Р – предикат суждения, выражающий часть дефиниенса в определении S, то суждение «S есть P» — аналитическое суждение.

Всякое суждение «S есть P» можно интерпретировать средствами подходящей 7a -Онтологии предикатом Mod¹²⁷(P*,S,a), где Р* — представление предиката Р как моды субъекта S. Здесь следует заметить, что в общем случае возможно двоякое понимание свойств. Традиционно свойства понимаются как имена в некотором языке, обозначающие некоторый аспект объекта. Такое понимание свойства можно обозначать термином свойство-имя. Но возможно понимание свойства и как того аспекта объекта, который выражается свойством-именем. Такое понимание свойства можно обозначать термином свойство-проявление. Например, в суждении «мяч — красный» свойство «красный» можно понимать и как одноместный предикат в подходящем логическом языке (это будет «красный» как свойство-имя), но можно понимать и как тот аспект реального мяча, в котором он проявляет себя как красный (это понимание «красного» как свойства-проявления). Свойство-проявление существует в самом объекте как одна из его сторон, один из аспектов его реального бытия, в то время как свойство-имя принадлежит языку. Свойство-проявление можно выражать как моду объекта в подходящей версии Проективно Модальной Онтологии. Так суждению «S есть P», где Р выражает свойство-имя субъекта S, сопоставим проективно-модальное отношение Mod¹²⁷(P*,S,a) – «Р* есть a -мода S», где Р* — свойство-проявление, соответствующее Р. Пусть Р_S – максимальный аналитический предикат субъекта S, т.е. дефиниенс определения S, P*_S выражает свойство-проявление, сопоставленное Р_S. Имеем: Mod¹²⁷(P*_S,S,a), и P*_S есть максимальная a -мода S из всех аналитических мод S. В оценке отношения P*_S и S можно встать на разные точки зрения. Например, можно предполагать, что субъект S исчерпывается своим определением, что будет выражено в равенстве (P*_S =a S). Либо можно посчитать, что субъект S больше только своего определения, включая в себя в том числе и свои синтетические свойства. В какой-то степени примирить эти позиции можно различением в субъекте S его аналитической S_A и полной S составляющих. S_A – это та часть логического субъекта, которая исчерпывается его определением, т.е. (P*_S =a S_А). S – вся полнота логического субъекта, проявляющаяся и в тех его свойствах, которые выходят за границы определения. Полный субъект содержит в себе аналитический субъект как свою моду: Mod¹²⁷(S_A,S,a). Если Q – некоторое синтетическое свойство субъекта S, то синтетическому суждению «S есть Q» можно сопоставить проективно-модальное отношение Mod¹²⁷(Q*,S,a), где Q* — свойство-проявление, соответствующее Q. Синтетичность Q* выражается также в том, что Щ Mod¹²⁷(Q*,S_A,a) – Q* не является a -модой аналитического субъекта S_A. Предицирование синтетическими модами Q* можно представить как результат действия логического интегродифференциала. Пусть

Mod¹²⁵⁶⁷(S_A,S,e,­,a) и Mod¹²³⁴⁷(Q*,S,c,Ї,a).

Тогда можно ввести логический e-интеграл i_e(S_A) =a S, «поднимающий» аналитический субъект до полного субъекта суждения и логический с-дифференциал d_c(S) =a Q*, «снижающий» полный субъект до его синтетического свойства Q*. На основе этих операторов можно ввести логический ес-интегродифференциал D _ec =_Df d_c° i_e, равный композиции е-интеграла и с-дифференциала, который сопоставляет аналитическому субъекту его синтетическое свойство: D _ec(S_A) =a Q*. Через такой интегродифференциал, выводящий за пределы аналитической составляющей логического субъекта, можно выражать акт синтетического предицирования, лежащий в основании синтетических суждений в теоретической философии Канта.