А как устроен мир звуков в восприятии человека, мир музыки? Какой там строй, каков по-рядок? Ведь слова музыка и гармония слились в нашем сознании. Музыка говорит непосредственно с сердцем…

Что же можно вспомнить о мире звуков для человека? Первое. Человек воспринимает силу звука в огромном диапазоне: от порога слышимости до порога боли .

То есть воспринимаемая величина меняется в пределах диапазона в 10¹² раз ¹. И что интересно, критическим для улавливания изменения громкости является не разность между двумя силами звука, а соотношение (множитель) по силе звука. Естественно, что при таком восприятии громкости одинаковое ее изменение будет соответствовать одинаковому соотношению сил звука. Эта особенность восприятия и огромный диапазон восприятия силы звука естественным образом привели к использованию логарифмических единиц для представления силы звука. То есть когда сила звука изменяется в 100 раз, на логарифмической шкале происходит изменение на 2 единицы (lg100=2). Тогда весь диапазон нормально воспринимаемой громкости укладывается в 12 единиц (lg10¹²=12). Интересно, что человек ощущает изменение громкости примерно в 1/10 этой единицы. Естественно, что такую «единицу чувствительности» приняли за основную единицу измерения силы звука. Называется она «деци-бел», как 1/10 бела ². Тогда нормальный динамический диапазон слуха составит 120 дБ ³ (дальше появляется ощущение боли, вплоть до смерти после 180 дБ).

Понятно, что каждый «децибел», являясь одинаковым по интервалу на логарифмической шкале, в переложении на исходную шкалу будет отличаться по длине ступени (количеству исходных единиц) от соседних на множитель . То есть 10 ступеней исходной шкалы, увеличиваясь каждая в ~1,26 раз, дают в итоге увеличение в 10 раз по отношению начала; или же 1 бел — по логарифмической (с основанием 10) шкале. А следующий 1 бел станет на исходной абсолютной шкале уже в 10 раз больше предыдущего бела. То есть каждый «бел» есть 10-кратное соотношение интервала на исходной физической шкале силы звука.

Можно видеть, как в полном соответствии с логарифмическим подходом к измерению силы звука (и воспринимаемой громкости) «высчитывается» особенность восприятия одинакового изменения громкости между 2-мя парами звуков. По известной из математики формуле и при получим (если lgA=a и т.д.) a-b=c-d (единиц). «Как учили…» После всего можно сказать: громкость звука для человека возрастает, по десятичному логарифму от физической силы звука…

Но вообще то громкость воспринимается человеком еще более не однозначно, субъективно. Субъективное ощущение громкости при одном значении силы звука будет разным на разных частотах, то есть при разной высоте звука. С наибольшей чувствительностью слух воспринимает громкость на частоте около 4000 гц (зона 2000 – 5000 гц). Звуки с изменяющейся от этой зоны частотой будут восприниматься «одно-громкими» — при увеличении силы звука. Чувствительность к громкости имеет и более-менее стабильный отрезок (при силе звука 70-100 дБ) на частотах 200 – 2000 гц. То есть на средних частотах, иже попадают на большую часть музыкального диапазона (см. ниже), мы, во-первых, гораздо лучше слышим, а, во-вторых, — стабильнее по частотам. С чего бы это? И за счет чего?...

Указанная зависимость человеческого восприятия громкости от частоты означает, что громкость двух звуков музыкального диапазона ощущается одинаково при большей силе звука на более низкой частоте; а при одинаковом увеличении силы звука громкость нарастает быстрее на более низких частотах.

Но громкость – это не главное в музыке (а тем более – в общении). Музыка — это, прежде всего соотношение высоты звуков (потом их длительность, а потом уж громкость и тембр). То есть, важен сам принцип и особенности восприятия высоты звучания, а потом, для музицирования — система построения соотношений этой высоты.

Так как же воспринимает человек изменение высоты звука?…

А здесь – похожая картина. Человек воспринимает различие по высоте звуков одинаковым не по разности значений частоты, а опять же — по соотношению (множителю) между частотами. Для него разница по высоте в 2-х парах звуков одинакова при одинаковом соотношении частот в них.

Еще Пифагор глубоко заглянул в физику соотношения звуков и гармоничного их восприятия. Он исследовал на монохорде («одноструннике» с возможностью кратного уменьшения длины колеблющейся струны) принципы гармонии созвучий и проектировал адекватный строй музыкальных инструментов. Проводя эксперименты, Пифагор установил 2 основных закона мира звуков. Первый: Человек слышит 2 звука созвучными (воспринимаемыми как один), частота ⁴ которых кратна через 2 (по степени 2). То есть продолжающийся ряд созвучных (консонансных) звуков будет образовывать последовательность соотношений: 1 – 2 – 4 – 8 – 16 — … С таким соотношением периодически возникающие на шкале воспринимаемой частоты звуки слышны, как один, имеют как бы одно периодически возникающее качество, естественным образом задают ритм основного интервала, основную макро-единицу шкалы музыкальных частот. Сейчас такой интервал частоты называют «октавой» (а почему?).

Именно такое степенное возрастание диапазона частоты между звуками одинакового «качества» соответствует тому, что мы слышим изменение высоты звука, как соотношение (множитель). Помните физическую шкалу силы звука и логарифмическую от нее шкалу восприятия громкости? Восприятие изменения частоты (то есть высоты) звука происходит также по логарифмическому закону: высота звука для человека возрастает, как двоичный логарифм. (А можно сказать «пропорционально логарифму», ведь любая пара логарифмов с основаниями X и Y связана множителем log_XY (=1/log_YX), например log₂A=3,322_*lgA.)

На шкале силы звука нет периодически возникающих подобных друг другу качеств, и ее десятичная периодичность («порядковость») задана только нашим «логарифмическим» восприятием. Здесь же внутренний ритм диапазона, пропорциональный степени «2», присущ изначально, как свойство высоты звучания в восприятии человека. А это уже интересно…

Наши предшественники ввели логарифмические белы также из-за огромного диапазона восприятия силы звука. Здесь такого диапазона не будет (а кстати – какой он?). Введение логарифмических ступеней внутри октав, если потребуется, будет связано только с особенностями восприятия. В этом случае , критерий количества ступеней «m» пока не понятен, но значение «k» будет близко к «1».

Основной период силы звука в 1 бел мы разбили на децибелы, как элементарные единицы восприятия. А здесь? Свои элементарные единицы, свои «децибелы»? В чем тогда будет элементарность этих ступеней для всей системы высот звука, в чем может быть их системная важность? Да мы еще и не все знаем о природе гармонии в соотношении высот звуков. Вернемся ка к истории.

Как говорят, Пифагор испытывал звуки, каждый раз оставляя звучащей какую-то часть струны монохорда: 1, Ѕ, ¹/₃, ј и т.д., — и сравнивал их звучание между собой. Он получал различные соотношения частот: ²/₃, ѕ, ⁴/₅. И здесь он услышал новые гармонии. Сейчас мы о них скажем, но прежде, заканчивая раздел экспериментов, интересно – до какой части звучащей струны он дошел? Не знаю. Но уже современные исследования установили другой факт: струна колеблется сразу многими своими частями. Говорят также, что любое колеблющееся тело не может колебаться менее, чем ¹/₁₆-ой своей длины, давая тем самым в пределе 16 обертонов. Так это или не так – нам здесь в принципе то не важно. Хотя и интересно. Ведь, если это – закон природы, то — не зря; в каких то подобиях он проявится…

Давайте сделаем табличку частей некой колеблющейся струны и присвоим частоту колебаний открытой струны в 24 гц (просто потому, что делится и на 2, и на 3, и на 4, и на 6; может пригодиться для «красивости» возможных дробных от нее значений).

Вот он – природный звукоряд. Его так и называют – натуральный (а еще – обертоновый). И что это за части – ступени внутри периода октавы? Это наши «окто-белы»? Н-е-е-т… Эта шкала – шкала абсолютных значений частоты, и изменяются ступени в пределах каждой октавы на одинаковую величину – на 24 гц. То есть не отражают эти ступени «логарифмического восприятия» человека (и не имеют отношения к «белам»). Чтобы отражали и тем самым были адекватными нашему восприятию, количество ступеней в каждом периоде-октаве должно быть одинаковым, а ступени внутри октавы должны отличаться от соседних на определенный множитель. Так что пусть остается этот «натуральный звукоряд» пока в стороне.

Так, и что же еще узнал Пифагор?

Пифагор, конечно же, использовал в своих опытах по определению созвучности несколько одинаковых монохордов. И он установил, что кроме благозвучия 2-х звуков, существует благозвучие 3-х. Второй музыкальный закон Пифагора гласит: Человек слышит трезвучие гармоничным (приятным), частоты звуков в котором находятся в отношении 4: 5: 6. Соотношение крайних частот этого трезвучия равно 1:1,5, и такой интервал сейчас называется «квинтой». Промежуточные внутренние интервалы в этом трезвучии равны 5:4=1,25 и 6:5=1,20; сейчас их называют соответственно большой (или чистой) терцией и малой терцией. Будем и мы их так называть.

И что же дальше сделал Пифагор? Ведь он искал для музыкальных инструментов такую градацию (ступени) по высоте извлекаемых звуков, чтобы:

1. количество ступеней было достаточно для получения мелодии

2. звуки в ступенях образовывали благозвучные сочетания

3. эти сочетания можно было получить для разных звуков (в идеале – для всех ступеней)

Что было дальше – можно реконструировать… Но давайте и мы сформулируем себе задачи. Мы уже знаем о принципиальном интервале-октаве, на границах которого звуки имеют одно качество. Понятно, что мы должны определить оптимальное количество ступеней (m) в пределах октавы, причем отличающиеся друг от друга одинаковыми сомножителями (). (Ведь мы знаем, как мы слышим равные по высоте ступени.) Тем самым эти ступени образуют для нас логарифмическую шкалу высот из неких «m-белов».

Тогда давайте узнаем теперь — что же слышит человек? Человек слышит звуки примерно от 16 гц (16 колебаний в секунду) до 20000 гц. А вот так называемый музыкальный диапазон гораздо меньше: от 16 до 4700 гц. Что вполне естественно: писк комара мы слышим, но исполнение мелодии на уровне «писка» музыкальным не назовешь; изобразить же комара можно и без воспроизведения его голоса.

А какое элементарное изменение высоты ощущает человек? Оказывается оно не одинаково на шкале частоты и возрастает: от 1 гц на низких частотах, примерно 3 гц на средних (возле 1000 гц) и до 5 гц — на высоких (более 3000 гц). То есть на самой низкой октаве (16-32 гц) мы можем услышать не более 16 ступеней. Значит или количество ступеней в октавах, будучи одинаковыми, не может быть более 16, или же в нижних октавах какие-то ступени будут нерабочими (неразличимыми).

Что, тем самым выбор сделан? Нет, делать окончательные выводы пока рано. Мы возможно еще не знаем всех проблем, всех приоритетов. Просто возьмем эти факты на заметку…

Так, теперь попробуем в пределах нескольких октав на каком-то количестве ступеней образовать несколько благозвучных «квинтовых» трезвучий. Кстати, музыкальный диапазон умещается в 9 октав (с запасом) от 2⁴=16 гц до 2¹³=8192 гц., а число квинт в музыкальном диапазоне будет 14: от 16_*1,5⁰=16 гц до 16_*1,5¹⁴≈4671 гц. Еще раз сформулируем задачу: мы должны определить количество ступеней в октаве так, чтобы внутри октав на этих ступенях (в идеале – на всех) можно было строить квинтовые трезвучия (интервалы: 1,5= 1,25^х1,2).

Подступимся к решению – от общего. Решение должно удовлетворять как минимум следующим общим условиям (не будем забывать, что мы ищем равномерное по множителю разбиение на ступени).

Первое условие (необходимое): должно быть хоть одно сочетание, когда некоторое целое количество квинт «m» совпадает по интервалу с целым количеством октав «n».

Второе условие (необходимое и достаточное): должно быть такое решение, когда некий множитель в какой-то целочисленной степени «m» равен «2», а в другой степени «n» – «1,5».

Показатели степени «m» и «n» совпадают по величине для обоих критериев: «m» означает сколько квинт отложено до «совпадения» с октавами и сколько равномерных ступеней-множителей будет тогда в октаве; «n» означает в скольких октавах «точно» отложатся «m» квинт и сколько равномерных ступеней-множителей будет тогда в квинте. Естественная связь 2-х условий.

Ну, что ж, проверим самое общее – первое условие: 2ⁿ = 1,5^m = aили .

Сделав следующее преобразование ,

получим .

Возьмем разность m-n=k, которая должна оказаться целочисленной (!): .

Очевидно, что это невозможно. Значит, нет таких значений «n» и «m», которые бы удовлетворяли первому условию. Значит, задача иметь единый множитель ступеней в квинтах и октавах не имеет решений.

С первого же раза попытка уладить квинты и октавы не приводит к рациональному и однозначному решению. Музыкальная гармония – иррациональна? Человек вынужден только приближаться к ней? Значит, задача стоит — в наиболее удачном приближении. Каков же критерий оптимальности такого приближения?...

Давайте посмотрим пока варианты, посмотрим все поле приближений. И останемся пока в рамках 1-го условия. Итак, из множества вариантов сочетаний квинт в октавах, посмотрим, в каких они сближаются максимально близко? Зачем? – чтобы, во-первых, знать — что и как получается здесь, — а, во-вторых, может быть получится построить октавно-квинтовый лад. В нижней таблице представлены первые шаги ряда квинт и ряда октав.

Чтобы сопоставлять варианты (иметь критерий) введем следующие коэффициенты:

– коэффициент, показывающий, во сколько раз отличаются частоты ступеней, посчитанных по «m» квинт и «n» октав (чем меньше он, тем ближе сошлись окончания рядов квинт и октав; и если он меньше «1», то квинты не доходят до конца октав),

– значение «октавных» коэффициентов для точного попадания в ряд квинт, то есть, какой должна быть величина «октавы» при данных «n» и «m», чтобы совпали ряды квинт и «октав» (если Q<2, то ряд квинт не доходит до конца октав).

Между «k» и «Q» есть взаимосвязь: .

«k» – основной (показательный) коэффициент; «Q» дает дополнительную информацию, но не определяет хорошего варианта.

В следующей двойной таблице сведены наиболее удачные варианты, при которых коэффициенты расходятся: «k» — с «1» в пределах 7%, «Q» — с «2» в пределах 3%.

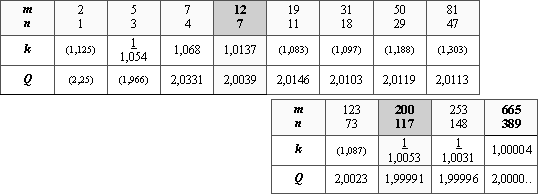
Примечательна вторая (нижняя) таблица. Здесь до значения ^m/_n=³¹²⁵/₁₈₂₈ встречаются 3 замечательных, но таких далеких варианта, находящихся вне «системного» ряда. Каждое из этих значений «ⁿ/_m » все ближе приближается к значению «», например, 117:200=0,585.

Ряд значений «m» и «n» первой таблицы имеет определенную закономерность или «систему»: два ряда Фибоначчи. Но эта закономерность не является абсолютной! Есть множество «^m/_n», при которых значение «Q» близко к «2», но при этом «k» далеко от «1» (интересно, что часто – это пары с простым числом, например, 43/25, 53/31). В то же время за пределами ^m/_n=⁸¹/₄₇ все больше увеличивается коэффициент «k» при том, что «Q» по-прежнему близко к «2» (приближаясь к некоторому значению Q≈2,011463…).

И все же значения «Q» периодически приближаются к «2» при значениях «n» и «m», соответствующим рядам Фибоначчи: 1-3-4-7- и 2-5-7-12-. Если сказать более строго: выражение при соотношении ^m/_n, как значений однопозиционных членов рядов Фибоначчи таких, что и , всегда имеет значение, близкое «2» с расхождением до ~1,2%. Интересно, а что и как тогда связывают отношения других пар рядов Фибоначчи?!

Первые шаги по новой «радиальной» тропке сразу за поворотом показало вот что. Обозначим ряды Фибоначчи по первым их двум членам, например, «1+3», «2+5» или «1+1». Отношения этих обозначений будет означать ниже отношение бесконечно последних соответственных (с одним порядковым индексом) членов этих рядов; а сами результаты отношений – значения, к которым стремятся эти отношения. Вот первые не до конца проверенные находки:

А это еще, что за странность – вглядитесь в 2 числа:

Эх, пройти бы дальше, да проверить? Надо бы, а вдруг – «галлюцинации». Но уж больно далеко будет. И так уж мы в стороне… Ладно нам остановиться, сделаем заметку, да вернемся чуть назад.

Вот еще отношение рядов:.

Ряд «1+1» — особенный, исходный (мы это знаем и еще убедимся дальше); он имеет интересные взаимосвязи с другими рядами в том числе, сдвигая порядок своих членов на некоторые позиции. Обозначим сдвинутый на одну позицию к началу (то есть последующий на место предыдущего) ряд, например, так: (1)-«1+1» или так ₁«1+1».

Тогда: .

И вот лежат еще соотношения:

Через качество этих отношений можно хотя бы почувствовать, что ряды Фибоначчи взаимосвязаны через Золотую пропорцию, а ряд «2+5» действительно имеет отношение к октаве и разбиению ее на множители-ступени…

Пожалуй, достаточно идти в эту сторону. Возвращаемся к развилке, к первой встрече с соотношением пар значений рядов Фибоначчи.

Подведем итог по первой верхней таблице. «Когерентные» пары значений в рядах квинт и октав в начале этих значений «подбираются» рядами Фибоначчи. А значит здесь снова – «Золотая пропорция»…

Информация эта нам пригодится дальше. Но уже сейчас можно видеть: во всей бесконечности вариантов, есть только 2 альтернативных. Но один из них – «обобщенный вариант» второй таблицы, — запределен на шкале частот; ведь, например, даже самый ближний из лучших «2¹¹⁷» > 10³⁵! В таком случае самый близкий наилучший вариант ^m/_n=¹²/₇, являющийся отношением четвертых членов рядов Фибоначчи, выглядит просто подарком. И надеждой, что можно будет найти рациональное и приемлемое приближение иррациональной гармонии звуков.

Имея надежду, попробуем определить «оптимальное» количество ступеней в октаве, следуя 2-му критерию: максимально близкому попаданию в октаву и квинту каких-то (?) количеств одних и тех же ступеней. То есть необходимо определить целое количество «n» и «m», чтобы: x^m=2и x ⁿ =1,5.

Сначала, опять же, проверим возможность (в принципе) точного, рационального решения.

Есть ли целочисленное «k» при каком-то «x», чтобы x^k = 1,[3] ? Однозначно решить — трудновато. Посмотрим вообще, как развивается эта зависимость; посмотрим, какими могут быть соотношения «n» и «m», чтобы получались решения для октав и для квинт при каком-то «x». Искать такие пары будем как раз по их разности – «k». Разность количества ступеней в октаве и квинте может быть равна 1, 2, 3 и т.д…

А какое при этом будет общее количество ступеней?

И как (каким ритмом) ступени будут выстраиваться внутри?

И потом, помните вопрос? – а как эти ступени позволят выстроить квинтовый аккорд 4:5:6 от всех таких ступеней?

Решение последнего вопроса является итогом наших действий и показателем успеха. Это решение – самое сложное в силу многовариантности. Именно через этот вопрос и будем решать всю задачу.

Посмотрим еще раз и подробнее структуру октавы и квинты. Октава имеет внутри два основных интервала (2 = ³/₂: ⁴/₃): квинту и интервал «⁴/₃»; его называют «квартой». Квинтовое трезвучие имеет два интервала, как мы уже знаем: чистую терцию (5/4) и малую терцию (6/5). Разница последних интервалов должна быть обеспечена разницей количества ступеней. Эта разница – самая маленькая среди наших интервалов. Очевидно, это и есть критический параметр для начала подбора вариантов. Начнем с разницы в одну ступень между терциями и выполним «укладку квинт»… Потом возьмем разницу в 2 ступени и т.д.

Каковы наши действия? Фиксируем ступени по интервалам квинтовых трезвучий, строя их от нижней границы (первой ступени) октавы — вверх и от верхней границы (от первой ступени следующей октавы) – вниз (назад). Если подробнее, то (1) строим квинтовое трезвучие, фиксируя тем самым два интервала-ступени; (2) затем от последней ступени – следующее трезвучие (с выходом из одной октавы); (3) затем от первой ступени следующей октавы строим квинтовые трезвучия назад (вниз), пока не выйдем за нижнюю границу октавы. По окончании отметим все «вышедшие» за пределы одной октавы ступени в одной октаве.

Фактически мы строим квинты от границы октавы, как от середины, вверх и вниз; с последующим переносом получившихся ступеней в одну октаву. Такое откладывание квинт в пределах 2-х октав и есть «укладка квинт» по-нашему.

В зависимости от того, каким количеством ступеней в терциях квинты мы зададимся (и соответственно – какой разницей между ними), мы получим разное количество ступеней в октаве, получим разные варианты… Путь – длинный и скучный. Но как часто во множестве вариантов, в бесчисленных пробах вдруг заблестит какая-то находка. Да и вроде бы другого пути у нас нет…

Конечно же, напрашивается — не угадывать и не подбирать, а попробовать сразу определить значения ступеней аналитически; например, для одной ступени разницы между терциями: . И тогда k=1,041[6]. Проверим, сколько таких множителей (то есть ступеней) построят октаву и насколько точно будет попадание. Так, 1,041[6]¹⁷≈2,001. Замечательно. Чуть ли не хочется воскликнуть: все готово! Но лучше не спешить, надо все же посмотреть, как укладываются квинты. Соответственно, когда между терциями квинты будут две ступени, межступенной множитель будет равен где-то около при 34 ступенях в октаве.

Но это все общие рациональные рассуждения. Без конкретного перебора вариантов, где будет видна вся картина, не обойтись. Начнем снизу и зададимся начальными ориентирами:

а). терции квинты должны иметь разницу в 1 или 2 ступени (пока хватит),

б). количество ступеней в кварте должно быть больше, чем в терциях и меньше, чем в квинте.

По этим условиям вариант квинты «2+1» не годится. Вариант «3+2» в квинте с «4» в кварте в принципе «проходит», но тогда в октаве будет всего 9 ступеней, и их едва ли хватит, чтобы между ступенями был более-менее одинаковым множитель; ведь при одной ступени между интервалами квинты требуется около 17 ступеней в октаве. Следующий шаг: квинта «4+3», кварта – от «5» до «6» (при построении будет видно), октава – от «12». С этого варианта и начнем…

Вероятно, первые варианты с двумя ступенями разницы появятся от удвоения вариантов «3+2» и «4+3». Давайте-ка, тогда предварительно рассчитаем следующую табличку. В ней мы сделаем подбор количества равномерно возрастающих (с одним множителем) ступеней в квинте и октаве так, чтобы отношения частот в них были близки к расчетным равномерным. В ее ячейках: в числителе – номер ступени, в знаменателе – значение множителя по отношению к началу.

Повторимся, эти коэффициенты-множители не являются округленными значениями корня n-степени из «2»; они только близки им, а в степени «n» примерно равны «2», но при этом, главное, — наиболее оптимально формируют квинту (то есть значения 1,25 и 1,5).

Множитель ступени		Кол-во ступеней в квинте (k=1,5)				Кол-во ступеней на октаву (k=2,0)
		Кол. ступ. между интерв-ми	1-ый интервал (k=1,2)	2-ой интервал (k=1,25)	Общий интервал (k=1,5)
	1,059	1	3 (1,188)	4 (1,258)	7 (1,494)	12 (1,990)
	1,047	1	4 (1,2017)	5 (1,2582)	9 (1,5119)	15 (1,9916)
	1,041[6] (1,25/1,20)	2	4 (1,177)	6 (1,278)	10 (1,504)	17 (2,001)
	1,038	1	5 (1,2050)	6 (1,2508)	11 (1,5072)	19 (2,0311)
	1,032	1	6 (1,2080)	7 (1,2467)	13 (1,5060)	22 (1,9996)
	1,029 (Ц 1,059)	2	6 (1,188)	8 (1,258)	14 (1,494)	24 (1,990)
	1,026	2	7 (1,1968)	9 (1,260)	16 (1,5078)	27 (1,9998)
	1,023	2	8 (1,1995)	10 (1,2553)	18 (1,5058)	31 (2,0237)
	1,0206	2	9 (1,2017)	11 (1,2517)	20 (1,5041)	34 (2,0017)

Ну что ж, теперь приведем схемы вариантов с тем порядком шагов «укладки» квинт, о котором мы говорили страницей назад (после вопроса «каковы наши действия»). Ход ясен из самих схем. А вот выводы попробуем сделать.

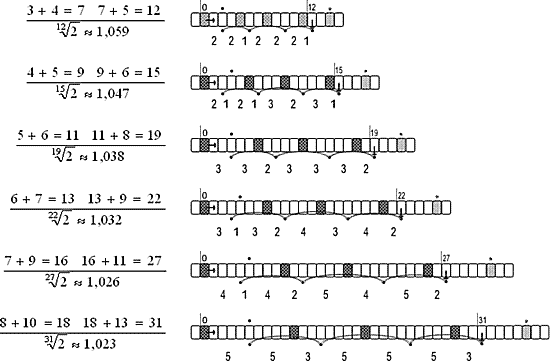
Удачными являются те варианты (1-й, 3-й и 6-й), у которых крайние левые ступени совпали на прямом ходу (верхняя перенесенная точка) и обратном ходу (нижняя точка). Удачными – в том, что между получившимися основными ступенями всего два типа интервалов (две группы промежуточных ступеней) и эти типы близки друг к другу по количеству промежуточных ступеней в них. Давайте по традиции эти две группы будем называть «тон» и «полутон». Итак, в первом удачном варианте (12 ступеней) в «тоне» — 2 ступени, в «полутоне» — 1; во втором (19 ступеней) – 3 и 2; в третьем (31 ступень) – 5 и 3; в четвертом… (прогнозируется) – 8 и 5.

А вот – и находки! Посмотрите – в «удачных вариантах» эти группы промежуточных ступеней (между основными ступенями) образуют последовательность ряда Фибоначчи! Интересно и то, что удачные варианты имеют четное количество ступеней в первом интервале (k=1,25) квинты, то есть здесь из четной степени берется квадратный корень () — известное выражение). Может быть мы еще увидим – в чем знаменательность такого случая…

Остается еще заметить, что во всех «удачных вариантах» получается по 7 основных ступеней с интервалами: 5 тонов и 2 полутона. Тогда, в октаве прогнозируемого следующего удачного варианта будет 5_*8+2_*5=50 ступеней, а в квинте – 3_*8+1_*5=29 ступеней…

Давайте-ка составим такую табличку.

Общая формула количества ступеней в октавах удачных вариантов: m_i = 5_*q_i + 2_*q_i-1.

Интересно то, что понятия «тон» и «полутон» становятся универсальными для всех удачных вариантов; просто количество ступеней в них – свое (и тоже фибоначчиево) для своих вариантов. Для всех вариантов количество «тонов» и «полутонов» в октаве – одно и то же. И это количество: 5 и 2, — совпадает с коэффициентами формулы.

Не таблица – а выставка рядов Фибоначчи в построениях разноступенных звукорядов. Конечно, источником таких последовательностей явилась выбранная схема укладывания квинт: с расположением границы квинт на границе октав. Можно попробовать другую укладку. Но, право, я пока не представляю более рационального (в положительном смысле), более вразумительного. Хотя можно пробовать. Но это – отдельная тропа. А еще и здесь — не все до конца пройдено. Может быть, пройдя до конца, мы сойдемся с другими тропами…

Глядя на эту таблицу, в которой стала наглядна фибоначчиева взаимосвязь всех интервалов октавы, хочется более подробно рассмотреть эти интервалы сами по себе. Сумма «высотных интервалов», образующих новый интервал, физически означает произведение множителей этих интервалов. Октаву составляет квинта и кварта:²/₁ = ³/_{2 *} ⁴/₃. И далее ниже: ³/₂ = ⁴/_{3 *} ⁹/₈. (Появившееся «⁹/₈ » – это интервал, называемый «секунда».) Квинта, составленная произведением двух частей, сама в произведении со своей старшей частью дает новое целое – октаву. А это и есть «принцип Фибоначчи», пусть и реализованный в произведениях (а не суммах) частей. Музыканты же так и говорят: секунда+кварта=квинта, кварта+квинта=октава…

Вы чувствуете, что здесь суммируются степени? Давайте продолжим этот ряд из последовательных произведений соседних членов. В сторону уменьшения следующий член составит ⁴/₃: ⁹/₈ = ³²/₂₇, а это (1,[185]) уже больше ⁹/₈= 1,125… Но следующее значение в эту сторону будет уже меньше 1,125… Если мы пойдем дальше, то увидим, как от исходного значения «⁹/₈»ряд своими членами «разбегается» попеременно к бесконечности и к нулю…

В сторону увеличения следующий член составит ³/_{2 *} ²/₁ = ³/₁, это – «октава + квинта»; далее ²/_{1 *} ³/₁ = ⁶/₁– «2 октавы + квинта». Запишем это так.

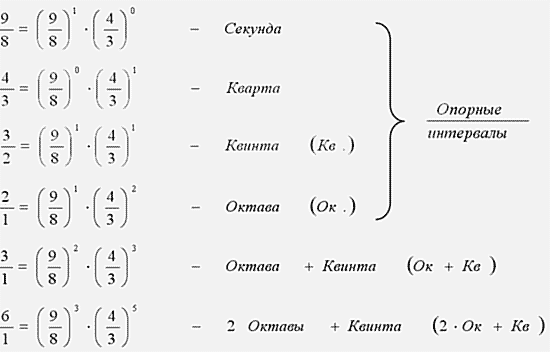
Из этой записи видна фибоначчиева зависимость в построении определенного ряда интервалов, основанных на октаве и квинте ⁵. Сама же октава как бы состоит из основных (опорных) интервалов: секунды, кварты и квинты. Можно сопоставить этот ряд интервалов с распределением «тонов» и «полутонов», как универсальных соотношений для всех удачных вариантов «построения» октав и квинт.

Значение	Формульные степени	Обозначение	Количество
			Тон+п/тон	Сумма
9/8	1 и 0	Секунда	1 + 0	1
4/3	0 и 1	Кварта	2 + 1	3
3/2	1 и 1	Квинта	3 + 1	4
2/1	1 и 2	Октава	5 + 2	7
3/1	2 и 3	Ок + Кв	8 + 3	11
6/1	3 и 5	2*Ок + Кв	13 + 5	18
18/1	5 и 8	3*Ок + 2*Кв	21 + 8	29
108/1	8 и 13	5*Ок + 3*Кв	34 + 13	47

Из таблицы видно, как взаимосвязаны полученные варианты музыкального строя и основные интервалы. Это просто один из «камушков» на весы «удачности», полученных выше вариантов музыкального строя. Ведь что-то не припоминается другой содержательный пример, чтобы ряд степеней в виде ряда Фибоначчи формировал на каком-то основании ряд имеющих смысл величин. А эти зависимости, кстати, обозначают некий класс дискретных функций:

, где F_n и F_m - значения какого-то ряда Фибоначчи…

Причем при сдвиге на любую «D» каждое новое значение «y_n» порождается произведением предыдущего значения и пред-предыдущего (принцип Фибоначчи в произведении»).

Может быть данный случай «примирит» как-то октавы и квинты?.. Посмотрим дальше.

Пифагор и его ученики (Архит), кстати, вывели еще одно правило созвучных интервалов, связанное со «священной Тетрадой» или как еще называют «треугольным числом»: 10=1+2+3+4. Отношения этих цифр и образуют опорные интервалы: 4:3, 3:2, 2:1 !

Мы знаем, что «удачность» эта – условна. Попытка уладить квинты и октавы (то есть уложить в них целое количество ступеней с равномерным темпом множителей) не получилось. Нет рационального решения для точного и равномерного распределения высоты по ступеням для октав и квинт. Музыкальная гармония – иррациональна. Это действительно та сфера, которая единственная способна со всей полнотой выразить человека… Потому и скрипка в руках мастера, точно воспроизводящего гармонию, воздействует сильнее (глубже), чем клавишные инструменты.

Но вопрос выбора музыкального строя требует определенности. К этому исходному вопросу и вернемся. Как же выбрать между удачными вариантами? В чем здесь может быть компромисс? Что является критерием отбора?

1. Количество ступеней, отражающих наше восприятие изменения высоты звука

2. Количество ступеней, удобное для музицирования

3. Количество, минимально искажающее восприятие «высоты звуков»

(из-за «неулаженности» октав и квинт)

По первому требованию ограничения возникают на нижних октавах при большом количестве ступеней, когда разница между соседними ступенями может составить менее 1 гц. Если будет принят вариант с количеством ступеней более 12 или 19, придется для инструментов низкого диапазона или широкого диапазона (фортепиано) учитывать в их конструкции это обстоятельство.

По второму требованию, опять же, при количестве ступеней в октаве, большем 12 или 19, очевидно, будут все настойчивей возникать проблема охвата ступеней пальцами рук. Как решение ее, потребуется какая-то конструкторская изощренность.

Третье требование – «фундаментальное», вокруг него мы кружимся во время всего поиска. Оно имеет 2 стороны, 2 родственные необходимости (потребности), без которых музицирование будет очень осложнено. Первая — необходимость играть мелодии, повышая или понижая их общее звучание, просто переходя в игре на аналогичную группу ступеней выше или ниже. Вторая – необходимость построения квинтовых аккордов от всех ступеней так, чтобы гармоничные звуки попадали на уже существующие ступени. Это общее требование можно сформулировать так: порядок и строй ступеней должен позволять воспроизводить мелодии с любой ступени. При равномерном возрастании ступеней – это получается естественно само собой. А как у нас?

Задаваясь каким-то целым количеством ступеней в разнице двух интервалов квинты, и тем самым – примерным множителем, мы получали разные варианты по общему количеству ступеней в октаве. Если бы мы руководствовались абсолютно «правильными» значениями, например, для 12 ступеней k=1,041[6], сохраняя этот темп для всех ступеней, мы не получали бы лучших интервальных значений квинты. Теперь мы имеем результат заложенной неточности множителя (мириться или нет, с которым будет видно сейчас), который может не позволить переносить мелодии по любым ступеням.

Вообще строй 7-ми ступеней получился, как помнится, «укладкой квинт» в 2-х октавах с расположением на их границе и границы квинт. Эти семь основных ступеней мы получили во всех удачных вариантах; между этими ступенями размещаются 5 тонов и 2 полутона. Кроме 7 основных ступеней варианты имеют промежуточные ступени: 1-й вариант «12» – 5, 2-й вариант «19» — 12, 3-й вариант «31» – 24. Вопрос, видимо, будет сводиться к содержанию этих промежуточных ступеней: помогают или мешают они разрешению 3-го требования.

Напомним, какую общую для всех вариантов картину мы имели при откладывании квинт. (Для экономии места и наглядности мы строили: сначала от нижней границы октавы – вверх, а потом от верхней – вниз.)

Указанные построения можно выразить следующими соотношениями в частотах.

Картина построения по частотам имеет отличия от построения по ступеням: расхождение в частотах 4-го трезвучия, прежде всего, 4,[4] и 9/2=4,5. Эту ситуацию мы увидим дальше. А пока – 4-е трезвучие будет просто сигналом.

Итак, получились заданные три трезвучия и следующие ступени одной октавы…

Перепишем их в ряд,

Мы получили реальные интервалы. Представим их в таблице, начиная от 24^x8=192 гц, как в представлении натурального звукоряда (помните?).

Мы построили трезвучия только от 3-х ступенек-нот (вверх): от «1», «5» и «4» (получив при этом, как результат, еще 4 ноты)... Причем во всех «удачных вариантах» (когда мы строили по количеству ступеней) это происходило подобно и давало 4 ступени в прямом ходе и 3 – в обратном (при разном, но имеющем фибоначчиеву закономерность, количестве промежуточных ступеней между ними). То есть получили общую группу 7-ми интервалов-ступеней.

Мы начали строить от первой ступени. А теперь надо строить и от остальных; и смотреть, как точно новые получающиеся ступени будут попадать на прежние. Сделаем это двумя способами – для проверки возможности обоих «потребностей музицирования».

По первой потребности-необходимости: будем строить 7 ступеней на единых табличных интервалах (как по шаблону) от каждой из этих 7 ступеней, то есть, как бы сдвигая строй по ступеням.

Результат представлен в таблице.

*) — Данные от второго значения — «202,5», — не приведены

**) — Данные от второго значения — «341,3», — не приведены

В этой таблице, кстати, интересным образом в интервале кварты (через 4 столбца на 5-ый) данные в столбцах имеют подобную структуру и подобный разброс (особенно в верхних 4-х строках). И выделяется, как «устойчивая» — средняя кварта на условных частотах «225» и «300». О чем это может говорить?

Для определения возможностивторой потребности музицирования: будем последовательно строить (откладывать) квинты по октавам в одну сторону. Здесь во всех «удачных вариантах» в первых 2-х октавах «зафиксируются» также 7 ступеней: 4 – в первой и 3 – во второй (различие с «граничной укладкой» (по 2-м октавам в обе стороны) будет по значению одной ступени). В дальнейшем по вариантам в каждой следующей октаве количество новых ступеней будет разным. Да и количество октав для «получения» всех ступеней будет меняться: все 12 ступеней 1-го варианта строятся 8-ю квинтами в 5-и октавах; все 19 ступеней 2-го варианта строятся 13-ю квинтами в 8-и октавах; и т.д. И здесь опять присутствует ряд Фибоначчи, то есть своим присутствием он дает оптимальное (гармоничное) решение рационального построения иррациональной действительности.

Итак, откладывание квинт в октавах.

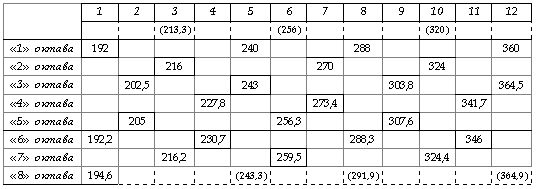
Говорят, еще Пифагор посчитал такую таблицу и обнаружил к своей печали несхождение квинт и октав. Это преткновение было названо «Пифагоровой коммой». Интервал-множитель «пифагоровой коммы» равен, как известно ~1,0137

В «удачных вариантах» (с числом ступеней в октаве 12, 19, 31, 50 и т.д.) при последовательном откладывании квинт всегда будет получаться одно и то же чередование «тонов» (0) и «полутонов» (-): -000-00-000-00-000-. Повторяющийся ритм этой последовательности, состоящий из 5 тонов и 2 п/тонов, и образует октаву (в ступенях). Причем не имеет значения, какой их повторяющейся последовательностью определить период-октаву, где начать ритм, где начать октаву.

В обоих построениях мы получили новые 5 ступеней, промежуточных первым – основным. Но увы – они не совпадают в одном и том же промежутке. И различия могут составлять более 3 гц.

Сведем результаты всех промежуточных ступеней. В нижней таблице заштрихованы частоты ступеней, встречающиеся в построениях «от каждой из 7-ми ступеней» (1) и «откладывании квинт» (2). Подчеркнуты ступени – полученные только по 1-му построению.

Для дальнейшего будем именовать частоты этой таблицы частотами «исходного строя».

Понятно, что не получается возможность легкого перехода из тональности в тональность в отсутствие равномерного темпа в ступенях, то есть одного коэффициента. Мы хотели сохранить точность квинт, кварт и октав, а не получается всё вместе, да еще и легкое музицирование. Добиваясь все же последнего и вводя для этого единый для каждого «удачного варианта» множитель ступеней, придется жертвовать чем-то в опорных интервалах. Тогда мы хотя бы узнаем цену легкого музицирования, чтобы принять решение. Сохраним обязательной точность октав, ее роль – становая, она держит основной ритм ⁶. То есть множители ступеней должны точно (!) приводить к ней, а как получатся при этом остальные интервалы – посмотрим.

Наилучшим будет тот вариант, где меньше расхождение в сопоставляемых ступенях с исходным вариантом. А цена будет оправдана, если разница ни одной пары сопоставляемых ступеней не будет больше элементарно слышимого изменения высоты звука (разумеется, среднего по способностям человека). В представляемом диапазоне частот (192–384 гц.) считаем «нормальным» (позволяющим соотносить ступени) расхождение – не более 3 гц (помните элементарную различимую разницу высот?).

Основания последних выводов надо представить полностью, эх — рановато лениться.

Рассчитаем и представим в таблицах равномерно темперированные строи с разным количеством ступеней и соотнесем получившиеся ступени с близкими из «исходного строя». В строках с «исходным строем», как и в предыдущей таблице, будут затонированы условные частоты, получающиеся в обоих способах проверки промежуточных ступеней (или выделены жирным шрифтом – для основных 7 ступеней), а подчеркнуты – получившиеся по 1-му способу.

Первая таблица – 12-ступенный строй.

Расхождение в соответствующих ступенях двух строев не превышает 3 гц! Все получившиеся ступени (и 7 основных, и 5 промежуточных) соотносятся с частотами исходного строя, «проходящими» в расчетах обоих «потребностей музицирования»! Из 12 ступеней 6 сходятся точно (менее 1 гц).

Следующая таблица.

Здесь целиком затонирована строка равномерно темперированного строя из 19 ступеней с коэффициентом . Выше – строка исходного строя.

Здесь в 2-х ступенях расхождение составляет 4 гц. Только 7 ступеней равномерного строя соотносится в ступенях исходного строя со средним вариантом, получающимся по обоим «потребностям музицирования», да и то — в основных ступенях, да еще с расхождением! И только 4 из 19 ступеней сходятся точно.

Ну и последняя (достаточно!) таблица.

Средние две строки (зигзагом) – расчетный равномерно темперированный строй из 31 ступени с коэффициентом:

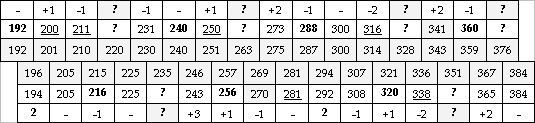
Здесь 6 ступеней вообще неясно с чем соотносить (велико расхождение). Со ступенями обоих «потребностей музицирования» исходного строя соотносятся только 8 ступеней (из них 7 — основные, и с расхождением). Только 6 из 31 ступени сходятся точно.

Динамика такова, что в последнем варианте появляются 6 лишних промежуточных ступеней! Вот и «мешающие», а не помогающие промежуточные ступени ⁷. Вот то, что и должно было проявиться: при худшем, чем у варианта «^m/_n=¹²/₇», совпадении октав и квинт появляются «чужие» ступени, попадающие совсем мимо. В вариантах равнотемповых ступеней только вариант «¹²/₇»дает промежуточные ступени, близкие значениями обоим «потребностям музицирования», причем с отличием не более 2 гц…

Можно называть еще какие-то аргументы в пользу очевидного варианта; перечислять преимущества по тем пунктам, которые были определены ранее. Но бывают случаи, когда не нужны дополнительные слова. Есть ощущение правильности, ощущение «внутренней правды строя», оправданности определенного строя… Не зря с самого начала в разных смыслах мы встречаем это соотношение «¹²/₇».Этот вариант как бы преподносится нам сразу… Мы честно и рационально пробовали найти другое решение… Никто не запрещает попробовать другим в продолжение или по другому. Но мы, кажется, выбор сделали.

В таком музыкальном строе созданы замечательные музыкальные ценности. Будем уважительны и к «букве наследия», которая сама создала уже свой пласт культуры и истории. Будем по хорошему консервативны. От добра — добра не ищут! Рациональное делать рациональнее – только портить…

Вообще, этот ряд «2-5-7-12» — действительно «музыкальный» ряд Фибоначчи ⁸. Он дает интервальную основу: тон-кварта-квинта-октава. Мы встречали эти числа и в других местах поиска…

Есть еще одна странность… Какая «музыкальность» в том, что соотношение средней рождаемости мальчиков и девочек равно коэффициенту (ступени) строя «¹²/₇»: 1,059 ⁹ ?...

А как же все сложилось в музыкальной культуре? Какой сложился стандарт уже практического музыкального строя?

7 основных ступеней получили особое общее название – ноты. И кроме того, как известно, каждая нота получила свое название, по порядку: до – ре – ми – фа – соль – ля – си – до. Говорят, названия эти появились из текста какого-то гимна, в котором каждая строка (и соответствующий слог!) начиналась как раз на основной ноте. Вопрос стоял о единой частоте какой-то ноты, о стандарте для написания музыки и настройки инструментов.

Замечательно, конечно, что фолианты нотных записей не зависят от конкретного значения этой ноты-эталона. Лишь бы все музыканты условились, что какая то нота какой-то октавы имеет такую то частоту. Ну и конечно, теперь, когда композиторы написали столько произведений, слыша определенное звучание, менять сложившийся эталон нельзя. А вообще история вопроса такова. В XVII веке исходным эталоном была «ля» ~420 гц ¹⁰. В XIX веке в музыкальной Европе установился эталон «ля» 435 гц. В начале XX века по предложению Американской федерации музыкантов была принята, как международный стандарт, исходная частота музыкального строя 440 гц — нота «ля» 1-ой октавы.

Почему же эталоном бралась позиция «ля»? Так повелось? Опять же, это – не принципиально. Хотя говорят, что когда-то где-то октава начиналась с этой ноты…

К слову сказать, эти 440 гц составили ¹¹/₈ от 320 гц (40_*2⁴), от «ля» 4-ой октавы мажорного звукоряда, построенного от 24 гц (помните, выше, наш исходный?). В этом звукоряде нотой «до» 5-ой октавы (от начала музыкального диапазона) является срединная нота квинтового «пифагорова строя» «384 гц». В современной музыкальной традиции 5-ую от начала музыкального диапазона октаву считают срединной, основной и называют «первой». Дальше вверх будет — «вторая», «третья» и так далее. А вниз — «малая», «большая», «контроктава» и «субконтроктава».

А каков сейчас конкретно строй музыкального диапазона по частотам?

Что ж посчитаем с нашим коэффициентом (1,0595) от ноты «Ля». Над «первой октавой» приведены частоты, как если бы они ставились по правильным квинтам.

Кстати, диапазон фортепиано распространяется от «Ля субконтроктавы» (27,5 гц) до как раз «Ре 5-й октавы». Фортепиано приобрело свой полный голос, свою общепризнанную популярность и стало «основным инструментом» лишь во второй половине XIX века ¹¹. Не случайно (во всяком случае – оправдано) тогда — такое совпадение диапазона фортепиано и выбранного эталона «Ля» 440 гц.

Кстати, для физиков, считающих от 16 гц, «ля» первой октавы имеет частоту 426,[6] гц (начальное «ля» физической субконтроктавы — 16 ^{х 5}/₃ = 26,[6]).

Ну, а почему октава называется «октавой»? Почему она называется от числа «8», хотя в ней 7 нот и 12 ступеней?

Вы помните натуральный звукоряд? В нем было 8 ступеней, причем одинаковых по абсолютному значению, то есть между ступенями были характерными не множители, а одинаковая разность, например, 24 — 27 — 30 — 33 — 36 — 39 — 42 — 45 — 48. Совместим его в одной таблице с исходным (неравномерным) строем (можно и с равномерно темперированным, у них по 7 соответственных ступеней).

Можно видеть, что, имея задачей размещение мажорных трезвучий, «пришлось» в природной октаве убрать седьмую ноту «¹⁴/₈», как «неиспользующуюся», к ней придвинуть ступень «¹³/₈», увеличив до «⁵/₃», а ступень «¹¹/₈» уменьшить до «⁴/₃». Конечно, никто и не думал об этом и не огорчился от этого. «Природный звукоряд» не является основой для построения музицирования; он лишь отражает физику колебания струны (любого тела). Но именно он содержит в себе 8-ми-ричное деление. Могло ли перейти отсюда понятие октавы? Нет, потому что это знание пришло позднее термина октавы. Можно ли сейчас так обосновать применение термина «октава»? Нет, потому что у них разная природа получения ступеней.

Октавная организация – такая же разрядная организация, как и десятичная система счисления. То есть количество цифр (нот) или интервалов между началами соседних разрядов (октав) и должно давать название системе. В музыке – это «7». Так почему же «октава»?

А квинта, имея интервал в 4 ноты, почему она — «квинта», то есть «пятая»? Потому же, почему «кварта» имеет не 4 ноты, как по названию, а только 3; также и другие далее. Названия их выстроены по общему ранжиру, по примеру октавы, для единообразия. Вплоть до того, что отсутствующий интервал между двумя одинаковыми нотами называется примой, то есть «1» там, где на самом деле «0»! Вот такой «королевский крокет» госпожи октавы.

Что за историческая драма или случай привели к этому? Хотя слово «октава» звучит лучше, чем «септава».

Но это дела давно минувших дней. А ведь с позиций математики в музыкальной октаве на самом деле 12 единиц. И мы уже знаем, что эти 12 ступеней октавы являются «беловой» шкалой. И имеют все основания называться «дуодеци-белами» (пусть здесь звучит проще – «дуобел»). То есть, например, между «до» и «ре» — 2 «дуобела», в октаве -1 «высотный бел» по основанию «2», первая октава ~ от 48-го до 60-го «дуобела», музыкальный диапазон составляет 99 «дуобелов», а весь высотный диапазон человеческого слуха – 124 «дуобела»… Даже похоже по размеру на диапазон громкости. (Эта похожесть еще интереснее, если вспомнить, что в некоторых источниках нормальный диапазон громкости оценивают в 130 децибелов, и тогда средней величиной будет 125 децибел. Точно также иногда предельно слышимую высоту оценивают в 22000 гц, и тогда средним будет примерно 125 дуобелов.)

Так мы прошли музыкальным строем, встречая везде стройные ряды Фибоначчи. Попадались фантики... Встретилось изречение. Великолепный Лейбниц, и он не остался в стороне от нашего путешествия: «Музыка — это бессознательное упражнение души в арифметике».

Поиски музыкальной гармонии попутно подарили и другие интересные соотношения:

Вообще, складывается впечатление (видится мираж), что любые выражения разности или суммы с φ₂/φ ₁могут быть приведены к произведению операторов φ₂/φ ₁, φ₀и t (или с суммой, где слагаемое «1»). Но это уже другая тропа, как бы ни манил мираж…

И посмотрите, сколько в восприятии и воспроизведении музыки собралось особенностей и каких-то исключений из общего правила. Удивительно, как все оказалось «приспособлено» к тому, чтобы человек мог исполнять и слышать музыкальную гармонию, мог насладиться согласным звучанием, а не слышать диссонансы, передавать свои переживания и сопереживать в гармоничном звучании, а не какофонии.

Ведь все было бы иначе, если бы было хоть одно:

1. Восприятие громкости не имело странно ровную зону в основной части музыкального диапазона на уровнях силы звука, соответствующих музицированию;

2. Воспринимаемый элементарный уровень изменения высоты звука не увеличивался бы вместе с повышением частоты, то есть вместе с абсолютной величиной самих ступеней;

3. Выстраивание дискретных ступеней по высоте звука при существующих законах благозвучности в октавах и квинтах не реализовалось бы оптимально в самом первом возможном варианте с минимальным количеством ступеней;

4. Этот вариант не оказался настолько хорош, чтобы на его основе сделать равномерную темперацию ступеней с возможностью после этого очень легкого и экспромтного музицирования.

На каждом этапе – подарки. Ведь восприятие звуков не обязано (с позиций эволюции) сопровождаться возможностью создания и воспроизведения не просто музыки, а огромного выразительного музыкального богатства; немузыкальных возможностей восприятия звука хватило бы только на простое чередование самых простых звуков. Всю свою родовую историю человек имеет аппарат слуха неизменным. Изначальна и приспособленность к музицированию. «Антропный принцип» и означает приспособленность окружающего мира к миру человека, к многообразию проявлений его телесной и духовной природы, к обеспечению этих проявлений… А Лейбниц говорил еще: «Миром правит Предустановленная Гармония»…

Любая шкала – это нарастание (изменение) какого-то параметра. Такое нарастание в природе происходит, видимо, равномерно по отношению к предыдущим значениям, то есть в определенном равномерном отношении, равномерном произведении. Природная шкала – это какая-то показательная функция (экспонента) – для реальных значений какого-то параметра, или какая-то спираль, как образ логарифмической шкалы. Беря логарифм от такой реальной природной шкалы, мы получаем для себя шкалу равномерного суммирования. Так и получается децибеловая шкала громкости звука (с реального отношения между единицами) и дуобеловая шкала высоты звука (с ).

Есть ли в Природе (в Космосе) какой-то процесс, имеющий иррациональную шкалу с (причем n – четное)?.. При, например, n=8 на отрезке 1-го разряда этой шкалы это будут следующие значения: 1 1,062 1,128 1,198 1,272 … до 1,618. И каждый промежуток между ними, как единицу, можно было бы назвать … Хотя названия дают лишь существующему.

Наша натуральная шкала – это арифметическая прогрессия. А природные шкалы устроены, видимо, — по геометрической. Мы для удобства «k» превращаем в «D ». Кстати, также поступает наш организм при восприятии звука. Но оправдано ли это в познании…

«Золотая пропорция» (φ₂или φ₁) в степенном ряду повторяет свойства ряда Фибоначчи; такой степенной ряд и является рядом Фибоначчи. Степени «Золотой пропорции» образуют логарифмическую шкалу. Реальная же физическая шкала как раз разбивается (при основании φ₂или φ₁) на величины, состоящие в отношениях нашего ряда Фибоначчи. Разница в «1» на логарифмической шкале соответствует множителю между соседними величинами на физической шкале; в данном случае это — φ₂(или φ₁). Только при таком множителе (и основании степенного ряда) эти величины образуют ряд Фибоначчи; при большем множителе физические величины «убегают» быстрее суммы предыдущих значений, при меньшем – «обгоняет» уже сумма.

Иллюстрация сказанного выше и уже известных до этого свойств ¹²: j ₂ ^i-1 + j ₂ⁱ = j ₂ⁱ⁺¹, откудаj ₂ⁱ + j ₂ⁱ⁺² = j ₂ⁱ⁺³ — j ₂^i-1. Интересно, что подобными ¹³ зависимостями обладает и «двойка»: 1,5_*(2ⁱ +2ⁱ⁺²) = 2ⁱ⁺³ – 2^i-1, причем2ⁱ + 2ⁱ⁺² = 10_*2^i-1 = 1,25_*2ⁱ⁺² = 5_*2ⁱ и2ⁱ⁺⁴ — 2ⁱ = 15_*2ⁱ = ¹⁵/_16*2ⁱ⁺³. Не правда ли – интересные цифры? Особенно, если вспомнить о сложных отношениях «октавы» и «квинты». Последние два свойства «двойки» имеют следующий вид в степенном ряду «Золотой пропорции»: j ₂ⁱ + j ₂ⁱ⁺² = t ²_{*j 2}ⁱ⁺²= (2j ₀ j ₂²)_{*j 2}^i-1

В нашем случае показатели степени над φ₂/φ ₁(являющиеся логарифмическими единицами) означают номер члена соответствующего ряда Фибоначчи (таких рядов может быть много в зависимости от коэффициентов). В основе же находится «Золотая пропорция».

Мы говорили о некой общей особенности нашего восприятия звуков – о логарифмической шкале над реальным миром. Основанием восприятия громкости является «10», основанием для высоты звука – «2»… Возьмем произвольную физическую шкалу степенных отрезков (aⁿ). Интересно отметить, что такая шкала степенных отрезков (aⁿ) заворачивается в логарифмическую спираль так, что эти отрезки размещаются между ортогональными осями (т.е. в ритме 90°). Эта спираль имеет формулу «aa ^/90° » и отсекает подобную же шкалу (a⁴ⁿ) на любом луче-оси (т.е. на оборотах 360° =4ґ 90°). И удивительно то, что октавная спираль «2a ^/360° » как раз и формирует образ скрипичного ключа…

А можно ли распространить эту закономерность одного типа восприятия на все восприятие ¹⁴ человека? Что тогда получается?..

Основанием гармонии является «j ». «Золотая пропорция» — наша суть, наша основа, наша подсознательная мерка… Мы в основе своей сущности имеем «Золотую пропорцию» как некий бессознательный оператор восприятия гармонии. Являясь воспринимающими субъектами, мы структурируем этим оператором (эталоном) физическую реальность в фибоначчиеву последовательность, но воспринимаем при этом только линейные показатели степени…

Если говорить о нашем общем восприятии, проводя аналогии с восприятием звуков, то натуральный ряд чисел – это ступени нашего восприятия, показатели степени над «Золотой пропорцией», и нашему линейному дискретному восприятию соответствует фибоначчиева структурированность реальности. Или по другому – нам дана в ощущение реальность единства целого и части, мы же остаемся на уровне восприятия отдельных дискретных единиц…

Если мы допускаем состояние единства целого и части, состояние, основанное на единении и согласии, символом (основой) чего является «Золотая пропорция», тогда меняется наше линейное рациональное мышление, мы проникаем в реальность, мы ощущаем многообразие, мы становимся способны радости и творчества. Человек каждый момент воссоздает свои отношения и тем самым – свой мир…

В рациональных решениях (проектах, исследованиях) — всегда противоречия полноты и цельности, «сказанности» и недосказанности (таковы отношения гармонии и алгебры). Лишь в иррациональных сферах обретают гармонию цельность и полнота. Там, действительно, звучит музыка, там царит интонация, проникновение, а не слова.

Чуть выше мы упомянули иррациональный ряд Фибоначчи. Зададимся еще раз вопросом о «природных шкалах».

Давайте представим ряды Фибоначчи и степенных значений j ₂ на числовой оси (или шкале). Шкала – это последовательность чисел, служащая для количественной оценки чего-либо. Привязывая числовой ряд к измерению какого-то параметра, мы создаем тем самым шкалу. Шкала – это числовой ряд, имеющий физическое значение.

На рисунке представлена сверху «природная шкала» с коэффициентом j ₂ между соседними значениями. Штрихами на общей оси «закреплены» также члены ряда Фибоначчи «1-1-2-3».

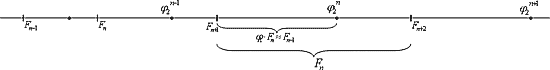
На ней воочию видно, что шкала степенных значений j ₂ сдвинута по отношению шкалы ряда Фибоначчи так, что ее отметки (ее числа) делят целочисленный промежуток между отметками шкалы Фибоначчи по Золотой пропорции.

Мы знаем, что ряд Фибоначчи в пределе стремится к Золотой пропорции. Тогда средняя формула может быть представлена, как сумма соседних по «n» членов ряда Фибоначчи: . Точность этой формулы зависит от «n». Понятно, что точность при отбрасывании дробной части (а суммируются то целые числа) нарастает за счет величины чисел, И тем не менее. Очередная иллюстрация сущностной взаимосвязи: и нарастающий ряд Фибоначчи отношением своих соседних членов колеблется вокруг значений j ₁ и j ₂, и нарастающий ряд степеней Золотой пропорции равен с нарастающей точностью сумме соседних через один членов ряда Фибоначчи.

И можно только еще раз обратить внимание на факт (вроде банальный, но – не здесь), что любые степени j ₂ состоят из целой части (рациональной) и иррациональной.

Вспомним формулу Бине:

Здесь: F_n є q^ф_n — «n-член» ряда «1-1-2-3»,

а L_n — «n-член» ряда «1-3-4-7».

Так называемый ряд Люка является дополнительным для основного ряда «1-1-2-3».

Все ряды Фибоначчи имеют свою пару.

Напомним формулы взаимосвязи таких рядов. Их можно записать следующими выражениями:

дополнительный ряд , основной ряд

Приведем правила, из которых будет видно, как (из каких взаимодействий) определяется начало рядов Фибоначчи. Условимся, что начало – это 1-ый член; и есть еще – «нулевой», далее которого идет «обратный ряд».

Сначала – триединое условие для основных и дополнительных рядов.

1. В основном ряду сумма 2-х членов через один не кратна «5».

2. В дополнительном ряду сумма 2-х членов через один кратна «5».

3. Члены пары основного и дополнительного рядов располагаются по отношению друг друга так, что выполняются 2 приведенных выше соотношения.

Для пары основного и дополнительного рядов имеются следующие свойства-следствия:

1. Основной ряд всегда начинается с меньшего члена (или равного второму).

2. Члены рядов за «нулевым членом» (в обратном ряду) имеют переменные знаки. У соответствующих членов основного и дополнительного рядов они – разные.

3. Сумма основного и дополнительного ряда дает удвоенный основной ряд, сдвинутый к началу на один член.

4. Все ряды, начинающиеся с «1» — основные, кроме рядов «1-3-4-7» и «1-8-9-17» (о последнем — см. ниже). Это единственные исключения, связанные с тем, что им соответствуют более «сильные» (онтологические) ряды: «1-1-2-3» и «2-5-7-12»!...

5. Кратные ряды являются такими же в своей паре, как и исходный им.

По этим правилам ряд «1-8-9-17» начинается на самом деле не с «1», а с «8». Вот где заявило о себе императивно и абсолютно верно «триединое правило начала ряда Фибоначчи».

Вернемся к преобразованию формулы Бине.

Если использовать формульные отношения между парными рядами, то можно получить следующее:

А после преобразований:

Полезные формулы. И красивые…

И можно привести обратную этим отношениям формулу:

Можно вспомнить также из прежних выводов общую формулу для разных степеней над j ₁:

Или так: .

А вот еще одна полезная формула. (Ну что за место… Прямо аптека, да и только – по полезности.)

И – красивая формула.

Мы не раз убеждались, что «1» идет сначала в сторону «j ₁». Если хотеть единообразия, то было бы правильнее, чтобы выражения с «Золотой пропорцией» строить именно через «j ₁», через значение «0,618», которое между «0» и «1». Но все же истина сама выбирает свою форму (единообразие – не однообразие).

•  ¹⁾  Кстати, сила звука пропорциональна квадрату звукового давления.
  
•  ²⁾ Белом называют любую логарифмическую единицу, то есть применительно к единице измерения любой физической сущности.
  
•  ³⁾ Кстати, 20 дБ соответствуют шепоту, 60 дБ – общему разговору или аплодисментам, 70 дБ – тихой игре на гитаре или пианино, 80 дБ – игре на гитаре медиатором; шумной улице, 100 дБ – фортиссимо оркестра 120 дБ – звук реактивного самолета в 5 метрах.
  
•  ⁴⁾ Правда, тогда это выражалось в соотношениях длины струны. Но мы то теперь знаем, что это одно и тоже, что частота колебания струны обратно пропорциональна ее длине.
  
•  ⁵⁾ Кстати, «октава» и «квинта» - это первые два шага приближения к j ₂ через отношения членов ряда Фибоначчи: 2/1, 3/2.
  
•  ⁶⁾ А вот Пифагор взял за основу квинту и построил свой лад в 12 квинт.
  
•  ⁷⁾ Кстати, они идут в интервале тонов (5) и полутонов (3) этого варианта: 3-5-(5+5)-3-3-(3+5).
  
•  ⁸⁾ Так же, как ряд «1-1-2-3» - «онтологический», «1-3-4-7» - структурно-системный». Сумма их (при неучастии первой «1» онтологического ряда!) и дает «музыкальный» ряд
  
•  ⁹⁾ С точностью ~0,044%. И с еще большей точность. ~0.0016% 1,059=j ₂³/4…
  
•  ¹⁰⁾ С такой частотой колебался в 1711 году и первый камертон придворного трубача английской королевы Джона Шора.
  
•  ¹¹⁾ Первым концертирующим пианистом, говорят, был Моцарт. Но лишь мощная музыка Бетховена сделала фортепиано «роялем» - королем инструментов.
  
•  ¹²⁾ Вид выражений с j ₁ понятно, как изменится, если исходить из того, что степенные ряды с j ₂ и j ₁ являются продолжениями друг друга и возрастают значениями в одном направлении, причем значения степени «i» располагаются на одной оси с отрицательными и положительными значениями: то есть в степенях над j ₁ знак перед числом изменится на противоположный, например, j ₁ⁱ⁺¹ + j ₁ⁱ = j ₁^i-1 .
  
•  ¹³⁾ Это подобие – формально, внешне; ряд «2 в степени» не образует фибоначчиевых отношений и не имеет последнего равенства без коэффициента. Подобные, но с большими коэффициентами, зависимости имеют и другие числа.
  
•  ¹⁴⁾ Вы не находите, что восприятие звуков несравненно ближе к психическому восприятию нежели столь «объективные», как зрение, осязание, вкус… Восприятие запахов тоже своеобразно; не зря говорят – «музыка запахов». Очень может быть, что человек воспринимает интенсивность запаха пропорционально логарифму реальной концентрации вещества…