|
|
|
Институт Ноосферного Естествознания - Публикации
Буданов В.Г.
Солнечная система, ближний космос, биосфера, человек и социум подвержены циклическим процессам, обладающим удивительным свойством подобия на разных иерархических уровнях эволюции. Одни и те же ритмы, или кратные им, можно встретить на разных масштабах реальности. Как объяснить это подобие и синхронность с позиций накопленного нелинейной динамикой опыта?
Сегодня развита мощная отрасль математики — фрактальная геометрия, которая все решительнее берется за описание природных объектов, к которым в принципе не могла подступиться обычная «гладкая» геометрия. В первую очередь это объекты имеющие эволюционное происхождение уже на самом примитином уровне, когда их формирование происходит шаг за шагом по некоторой более менее фиксированной программе — итерационной процедуре. Будь то образование береговой линии, кораллового рифа, кроны дерева, облака или делящегося живого организм. Пространственные формы, структуры таких обьектов обладают замечательными свойствами самоподобия на разных масштабах, и если они имеют еще и фоновое движение в структуре, то неизбежны самоподобные временные процессы на таких объектах — фрактальные временные ряды. Их избегают экспериментаторы, зачастую просто не видят их, а природа подбрасывает в эволюционных задачах именно такие негладкие закономерности. Попробуем разобраться в чем ограниченность традиционных подходов к описанию времени в эволюционирующих системах и предложить конструктивную альтернативу.
Дело в том,что при описании системы как части Универсуума мы с неизбежностью вынуждены отнести часть физических факторов, к внешним для нее, а часть к внутренним. Аналогично принято поступать и с ритмами — деление на экзогенные и эндогенные (внешние для системы и внутренние). Но ритм есть свойство целостной системы, и такое разделение, вообще говоря, не всегда правомерно. Хотя именно так возникает идея причинно-следственных влияний планет (возможно опосредованно через Солнце) на биосферу, а в древности родились астрологическая эмпирика и язык (напомним, что А.Л. Чижевский так и называл гелиотараксию, свою науку о солнечно-земных связях, — «новая астрология»). Плодотворность этого подхода безусловна, но далеко не всегда множество корелляций и синхронизмов явлений можно объяснять их причинно-следственной связью. Общая причина может быть совершенно иной (люди засыпают не потому, что влияют друг на друга, а потому, что приходит ночь).
Но возможна и другая, альтернативная, точка зрения, когда на каждом иерархическом, квазизамкнутом, уровне доминирует лишь один, или малое число экзогенных или даже автоколебательных эндогенных ритмов- водителей (говоря синергетическим языком — параметров порядка), которые универсальным образом порождают богатый спектр эндогенных внутренних ритмов системы, в некотором смысле подобных эндогенным ритмам других уровней. Такой универсальный механизм должен существовать, т.к. Универсуум имеет только эндогенные ритмы (всякий экзогенный ритм является эндогенным для объемлющей системы), ритмы самоорганизации сложного. При последнем подходе ожидать причинноследственных корреляций всех подобных ритмов видимо не приходится, хотя синхронизация вполне возможна. Дело в том, что в последние двадцать лет теории динамического хаоса, диссипативных структур и синергетика раскрыли систему и связали ее в точках бифуркаций со всеми уровнями реальности за счет сверхсенситивности динамических структур хаоса (7 — 9, 12), что позволяет оправдать гипотезу синхронизации экзогенных и эндогенных ритмов, сами же эндогенные ритмы — автоколебательные структуры в диссипативных системах (например химические часы) зачастую вообще не требует никаких внешних периодических воздействий (Белоусов—Жаботинский—Пригожин). И все же, вместе не значит вследствии, и многие иллюзии локальной причинности придется оставить, но возникнет глобальная, эволюционная причинность ритмической ткани Вселенной.
Следует сразу уточнить, что речь не идет просто о комбинационных резонансных частотах нелинейной системы (обычно среди них много «лишних»), и что мы понимаем под ритмом не только и не столько синусоидальный бесконечный ритм, но скорее жесткую в своих пропорциях программу развития и функционирования сложной эволюционирующей системы. Именно так можно подходить к развитию не теплокровных животных и растений, образующих большую часть биосферы, особенно стадий эмбриогенеза (программа развития за счет автономных запасов питания), когда внутренние химические часы — период митотического дробления — могут менять свой физический темп хода в разы в зависимости от естественных колебаний температуры среды, совершенно не кореллируя ни с какими внешними ритмами.
Истина как всегда должна быть посередине, но наша цель раскрыть возможности именно второго, почти не исследованного подхода, поскольку для его описания еще недавно не было ни математических методов нелинейной динамики, ни синергетической методологии.
Итак, мы вновь ищем законы холизма, законы самосборки реальности, но теперь понимая, что они нелокальны ни в пространстве ни во времени, но функционально самоподобны на разных масштабах, что на манер полевых теорий бутстрапа, позволяет повторять вечную формулу — «все во всем».Далее мы основываемся на идеях и результатах полученных автором в (3,4).
Структуры в нелинейных развивающихся системах могут возникать (существовать) или напротив исчезать (отсутствовать) в областях нелинейных резонансов, известных еще со времен Пуанкаре, а принципы гармонии отражают простейшие правила приоритета, очередности рождения этих структур. Создавая своего рода правила суперотбора — морфогенетичекую волну, и кардинально сокращая время эволюции Вселенной.
Фактически это означает наличие дополнительных факторов направленного нестихийного отбора, сомосогласованную эволюцию минимум двух иерархических уровней: квазиконсервативного и диссипативного, последний в процессе структурных переходов создает параметры порядка и новые частоты, пополняя моды первого, которые резонируя, инициируют эти структурные переходы. При таком механизме последовательно реализуются не все возможные резонансные структуры, а лишь энергетически ближайшие.
В столь общей формулировке это скорее руководство к действию, метаидея, требующая всякий раз контекстуального воплощения.
Сначала покажем как работает эта идея в нелинейной системе с достаточно богатым спектром частот, порождаемым двумя базовыми частотами 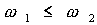 . Это могут быть как эндогенные, так и экзогенные ритмы системы, важно, чтобы система была достаточно сложной, и могла структурно поддерживать в своем развитии высокие комбинационные частоты. Тогда наиболее сильный резонанс и, следовательно, вероятность возникновения структурной перестройки будет происходить на ближайших комбинационных частотах
. Это могут быть как эндогенные, так и экзогенные ритмы системы, важно, чтобы система была достаточно сложной, и могла структурно поддерживать в своем развитии высокие комбинационные частоты. Тогда наиболее сильный резонанс и, следовательно, вероятность возникновения структурной перестройки будет происходить на ближайших комбинационных частотах 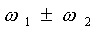 . После такой перестройки возможен структурный резонанс на следующих ближайших комбинационных частотах
. После такой перестройки возможен структурный резонанс на следующих ближайших комбинационных частотах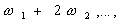 и т.д.. Этот процесс образует волну структурных перестроек в пространстве резонансных частот системы. На каждом шаге существует максимальная частота, которая имеет тот же генезис, что и ряд чисел Фибоначчи, так как она равна сумме двух максимальных частот на предыдущих шагах, а следовательно отношение максимальных частот для двух последовательных шагов структурных перестроек стремится к золотому сечению с увеличением числа шагов, если конечно система поддерживает перестройки на высоких частотах. На n-м шаге максимальная частота дается простой формулой
и т.д.. Этот процесс образует волну структурных перестроек в пространстве резонансных частот системы. На каждом шаге существует максимальная частота, которая имеет тот же генезис, что и ряд чисел Фибоначчи, так как она равна сумме двух максимальных частот на предыдущих шагах, а следовательно отношение максимальных частот для двух последовательных шагов структурных перестроек стремится к золотому сечению с увеличением числа шагов, если конечно система поддерживает перестройки на высоких частотах. На n-м шаге максимальная частота дается простой формулой 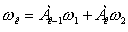 ,где
,где 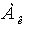 — члены стандартного ряда Фибоначчи.
— члены стандартного ряда Фибоначчи.
В общем случае многих базовых частот все приведенные выводы остаются в силе, а две частоты порождающие волну резонансов ЗС это максимальная частота и ближайшая к ней. Причем огибающая максимальных частот структурных перестроек растет по закону Фибоначчи.
Отметим, что процесс может инициироваться даже одной частотой, но породившей за счет сильной нелинейности структуру на ближайшей второй гармонике, тогда дальнейшее структурирование идет как было описано на суммарных и разностных частотах, и максимальные частоты пропорциональны стандартному ряду Фибоначчи 1,2,3,5,8,...; возможно это и объясняет его особую распространенность.
Легко показать, как достраиваются все меньшие члены ряда Фибоначчи на разностных частотах, а затем порождается ряд для квадрата ЗС, но все эти условия не обязательно граничные для системы с многими базовами частотами.
В отличие от обычных подходов к изучению ЗС мы стартуем с временного спектра, а не пространственной формы, т.к. считаем, что: во-первых, это проще и диктуется самой идеологией исследования нелинейной динамики, а во-вторых единственно правильно, т.к. спектр форм в развивающейся системе будет повторять правило ритма ЗС, но в сжимающейся последовательности, лишь для достаточно материально однородных структур со слабой дисперсией (слабой зависимостью скорости волны от частоты), поскольку характерный размер структур порядка v/w. Если же материя существенно неоднородна, что чаще бывает, то пространственные формы нарушают симметрию ЗС, и временная симметрия ЗС становится скрытой.
Таким образом можно предположить, что золотое сечение встречается много чаще на уровне временных спектров, нежели в пространственных формах (здесь надо оговориться — мы смотрим за эволюцией спектра). Быть может поэтому столь доступен для восприятия язык музыки: консонансы есть отношения первых членов ряда Фибоначчи и их дополнения до октавы.
Прекрасной иллюстрацией нелинейного временного подхода к частной эволюционной задаче ЗС является работа К.П. Бутусова(2), в которой ЗС появляется как резонанс самосогласованного формирования соседних орбит планет. В нашем подходе ЗС — ассимптотическое свойство целостной системы, последовательно проходящей фибоначчивы структуры часть из которых может и исчесзнуть к моменту наблюдения, что, например, справедливо для планетных орбит. (Бутусов)
Может возникнуть вопрос, как столь простой механизм мог остаться незамеченным ранее? Дело в том, что физика овладела идеологией диссипативных структур совсем недавно — лет двадцать (химическая кинетика, турбулентность, плазма и т.д.), в то время, как теория консервативных систем развивалась более ста лет в совершенно других предметных областях (небесная механика, теория колебаний, теория поля и т.д.), их первая встреча возникла при построении резонансных моделей происхождения и эволюции Солнечной системы (А.М. Молчанов (12),А.М. Чечельницкий (5), П.К. Бутусов (2)); к живым системам такой подход просто не применялся. Кроме того, известно расхожее мнение, что ЗС есть признак лишь живых систем, и не встречается в неживой природе, сейчас мы понимаем, что это не так, просто время эволюции целостных, по настоящему сложных «неживых » систем слишком велико для нас, впрочем, как и масштабы. Правильнее говорить, что ЗС есть признак эволюционирующих систем, обладающих достаточно богатым структурным иерархическим потенциалом, а так же механизмами наследования и коммуникации (внешней и внутренней). (как говорил А.М.Молчанов (1966), — «...зрелая эволюционная система неизбежно резонансна»). Фактически такой подход размывает понятие системы, слишком открыта она к обоим, мега и микро-уровням; слишком организмичным становится сам порождающий Универсум, а система — похожей на него. Это свойство эволюционирующих систем обеспечивается в фазах становления за счет креативно-коммуникативного свойства динамического хаоса — непременного условия порождения структуры. Динамический хаос обладает одним замечательным качеством — сверхчувствительностью, он открывает систему внешнему миру. Понятие замкнутой изолированной системы становится недостижимой идеализацией. Система вступает в диалог со Вселен- ной, она причащается Универсуму, ощущает себя его частью и подобием. Именно в хаотических эволюционных фазах возможно восприятие, получение информации из целостного источника, синхронизация и гармонизация системы в согласии с космическими принципами. Подробнее о роли динамического хаоса в эволюционных процессах см.(6).
Наше объяснение носит достаточно универсальный характер и позволяет прогнозировать и целенаправленно искать (создавать) системы эволюционирующие по принципам ЗС.
Вместе с тем, не всегда и не сразу порождающие иерархические уровни столь контрастно отличаются своей консервативностью от порождаемых диссипативных уровней. И здесь можно предложить еще один универсальный механизм эволюции.
Со времен пионерских работ А.Л.Чижевского стало ясно, что искать ключ к единству мира следует в установлении законов подобия эволюции различных частей Вселенной и механизмов синхронизации этих частей.
Одним из основных ритмических принципов пронизывающих реальность является октавный принцип, согласно которому структуры формируются сериями преимущественно на частотах кратных, либо дробных степеням двойки от некоторой частоты характеризующей данную серию(М.А.Марутаев называет это качественной симметрией (1)). Еще недавно основным аргументом в его пользу была неизбежность возникновения в нелинейной системе ближайшей второй гармоники, но помимо нее существуют также и высшие гармоники и комбинационные частоты; кроме того дисперсия масштабов структур порождает дисперсию частот, размывающую обычный процесс удвоения. По нашему мнению, выделенный статус процесса удвоения частоты (или периода) в сложных эволюционирующих системах, и принципах гармонии в частности, связан с универсальным масштабноинвариантным сценарием перехода к хаосу (выхода из хаоса) в нелинейных динамических системах, с так называемым каскадом удвоения Фейгенбаума (12).
В более общей ситуации в системе возникают так называемые структуры А.Н. Шарковского (9) на периодах кратных 3, 5, 7,.... от основного, т.е. октавные серии от нечетных гармоник. Именно этим можно объяснить эффективность полукачественных подходов в ритмологии использующих такие серии, см. (6). Мы же ограничимся чистой октавной серией, но предположим, что она развивается в иерархизирующейся системе, что позволит нам воспроизвести и структуры Шарковского и исследовать более тонкие эффекты. Однако сам по себе октавный принцип не может ухватить всех тонкостей перестроек эволюционирующих структур, и здесь принципиально необходим учет иерархии ритмов, их взаимой синхронизации. Мы предлагаем реализовать это следующим образом (3, 4) —
1. «Принцип максимума темпа роста ритмокаскадов» — сразу по завершении очередного периода происходит бифуркация его удвоения (увеличения или уменьшения вдвое), так последовательно образуется временной (прямой или обратный) ритмокаскад. То есть прямой или обратный каскад Фейгенбаума, в котором точки бифуркации синхронизованы с концами периодов. Это действительно самый быстрый каскад Фейгенбаума, при котором еще имеет смысл говорить об октавном принципе. Обычно же предполагают адиабатическую зависимость внешних параметров от времени, когда между ближайшими точками бифуркации совершается много колебаний с одним периодом.
Отметим также возможность иной, информационно-структурной интерпретации принципа: множество всех подмножеств системы из N элементов содержит подмножеств, тогда постулируя постоянство скорости обработки информации в системе (одно подмножество в единицу времени), получаем принцип максимального роста как закон удвоения периода обработки информации при увеличении объема системы на 1 элемент, последовательное добавление элементов и ассоциируется с чередой структурных перестроек, как скачков информационного объема обработки при расширении системы.
2. «Принцип иерархической синхронизации ритмокаскадов» — в момент бифуркации в некотором ритмокаскаде все параллельно развивающиеся в системе младшие ритмокаскады (т.е. имеющие в данный момент меньший период) обрываются и стартуют- синхронизируются вновь от точки бифуркации по старшинству. Таким образом младшие ритмокаскады «живут» и свободно развиваются в промежутках между моментами бифуркаций старших, «рождаясь» и «умирая» в эти моменты.
3«.Принцип фрактальности — масштабной полноты ритмокаскадов» — в системе одновременно существуют все ритмокаскады, непротиворечащие постулатам 2 и 3. Тогда дерево ритмокаскадов является фракталом, реализующим нелинейную природу времени самоорганизации. В реально проявленной системе реализуются далеко не все ритмокаскады, т.к. могут существовать дополнительные принципы запрета и ограничения — пространстенно-временное окно существования системы, материальные условия, случайные внешние факторы, и т.д.. В таком, наиболее жестком варианте, выполнение этих принципов тем точнее, чем выше организация системы, чем больше число ее иерархических уровней и совершеннее механизмы памяти и наследования. Поэтому в первую очередь речь идет о живых ситемах и организмах.
Приведем общую формулу для дерева ритмокаскадов порождаемых одним ритмом, в случае только прямых ритмокаскадов Фейгенбаума. Здесь аргументы — есть номера соответствующих бифуркаций в различных поколениях ритмокаскадов (иерархических уровнях), а сама левая часть задает моменты бифуркаций.
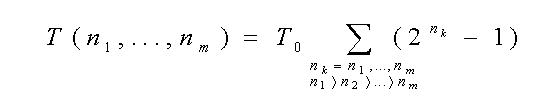
причем существенно правило упорядоченности аргументов согласно правой части, которое и есть правило запрета на нарушение заполнения дерева ритмокакадов. Развернутая на рисунках структура возникающего временного ряда имеет самоподобный фрактальный характер. В работе (14) нами показано, что этот ритмокаскад обладает свойством экстремальности — максимальной скоростью роста, т.е. активизации все новых уровней, по сравнению с другими иерархическими законами фрактального роста.
Этот подход применяется ниже для объяснении некоторых закономерностей эмбриогенеза животных и онтогенеза человека. Для сложных природных мегасистем — биосфера, Земля, Солнечная система мы слабо представляем их эволюцию за пределами нашего квазисинхронного среза. Одако и здесь удается обнаружить октавный принцип организации ритмов Солнечной системы, ритмокаскадные корелляции ритмов ближнего космоса и структурных перестроек процессов развития живых систем, активности Солнца, потоков космических лучей на Земле и активности магнитосферы нашей планеты. Хорошо известна связь этих ритмов с биосферными процессами, но теперь природу этой связи можно искать не в дальнем космосе, за счет влияния планет, а в достоверных эффектах воздействия движений Земли, Луны и Солнца, чей физическо-химический механизм воздействия на живые объекты более менее ясен.
Приведем явный вид дерева ритмокаскадов до девяти бифуркаций в первом поколении.
Кризис старшего «0»-го порядка включает в себя несколько младших кризисов
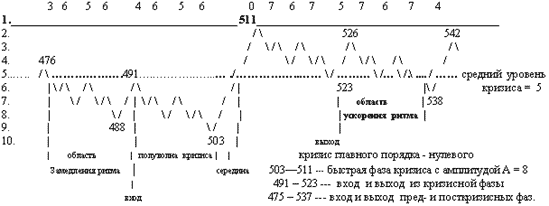
Здесь по горизонтали отложено время в единицах основного периода ритма-водителя, а по вертикали даны номера структурных иерархических уровней системы, последовательно прорабатываемые ритмокаскадами с тем же номером поколения.
Легко заметить, что ни на одном уровне не существует сколь угодно долгого периодического процесса, всегда он рано или поздно обрывается, а затем возрождается вновь, хотя на первом уровне не существует ни одного периода! Например, на втором уровне период 2 непрерывно повторяется не более 4 раз, период 4 не более 5 раз, а на 3 уровне не более 12 раз …, после чего ритм исчезает на некоторое время.
Но система имеет конечное число иерархических уровней, поэтому дерево ритмокаскадов не может расти бесконечно долго и система завершает свое развити вычерпав структурный потенциал — это и есть ее предельно возможное время жизни. По завершении полного цикла жизни, он видимо может повторяться многократно по законам объемлющей системы, например линейный ритм с периодом равным времени жизни системы. Поэтому время жизни системы может быть периодом ритма водителя для большей системы и т.д..
Следующим специфическим свойством дерева ритмокоскадов является наличие зон трансформаций-кризисов, или структурных резонансов — резких структурных перестроек системы от низших к высшим уровням. Максимальные трансформации предшествуют точкам последовательного удвоения основного периода. Этой бурной, быстрой фазе предшествует «полуволна» вхождения в кризис и симметричная «полуволна» выхода из кризиса относительно среднего уровня между минимальным и максмальным уровнями, само вхождение предваряется эффектом замедления (в геометрической прогрессии со знаменателем-2) колебаний касающихся среднего уровня. Предкризисное замедление характерных ритмов перед точкой бифуркации отвечает хорошо известной теореме в теории катастроф Рене Тома. На рисунке это показано на примере кризиса 503-511.
Кризис мы будем характеризовать его средним уровнем, амплитудой А (полным числом трансформируемых уровней) и старшинством — порядком (на сколько единиц его амплитуда меньше амплитуды ближайшего предшествующего главного кризиса), все остальные характеристики (полуширина, время замедления, положение на временной оси, максимум и минимум) однозначно с ними связаны. Главный (нулевой) порядок имеют кризисы удвоения на первом уровне (ритмокаскад старшего поколения), они имеют максимальную амплитуду из всех предшествующих, все остальные кризисы побочные. Будем также говорить о длительности самого кризиса, его быстрой фазы и длительности полного кризиса, т.е. включая пред — и пост- кризисные фазы. Числа в самой верхней строке указывают порядок соответствующих кризисов, Мы видим, что кризисы устроены самоподобно фрактальным образом, и все области кризиса старшего порядка, исключая зону быстрого роста, образованы перекрывающимися кризисами младших порядков.
Приведем еще выражение для продолжительности кризиса, как функции его амплитуды А=2k., тогда: время бурной фазы в периодах ритма водителя равно 2k; время между входом и выходом в кризис (две полуволны); а полное время кризиса включая пред посткризисные фазы. При этом относительная ширина кризиса быстро стремиться к нулю с увеличением k, быстрее чем. Отметим, что начало и конец пред- пост кризисных фаз принадлежат обычно и соседнему кризису с амплитудой вдвое меньшей или вдвое большей, т.е. кризисы близких порядков сильно разнесены, тогда в окрестности главных кризисов будет наблюдаться относительное затишье. Мы привели формулы для четных амплитуд, в случае нечетных амплитуд кризис видимо не симметричен и его левая (правая) половина проходит как кризис на единицу меньшей амплитуды, тогда другая на единицу большую амплитуду (если мы пытаемся сохранить квант времени).
Дадим в взаключении формализованной части значения главных («0»- порядка) максимумов -1, и минимумов -N, а так же побочных максимумов и минимумов«1»-порядк / 2 + / 4 — 2, и / 2 + / 4 — N +1 соответственно.
При больших временах максимумы разных порядков все точнее приближаются к временам, задаваемым структурами А.Н. Шарковского, а их попарные отношения дают гармонические законы целочисленных отношений умноженных на, Что ассимптотически оправдывает гармонический подход развитый в (3,6).
Самоподобие, фрактальность нашего временного ряда объясняется фунциональным самоподобием итерций его построения. Ряд от данного «0» максимума до ближайшего последующего «0» максимума получается из всего ряда предшествующего данному максимуму опусканием его на один уровень.
Дадим теперь ряд иллюстраций метода в применении к сложным эволюционирующим системам Солнечной системы, биосферы и организмов. Мы ограничимся рассмотрением лишь трех основных экзогенных физических факторов: период вращения Солнца, годовое и суточное вращение Земли, период обращения Луны, период 160 минут—пульсаций магнитосферы около солнечного пространства, которые порождают практически все известные на сегодня ритмы в диаппазоне от долей суток, до сотен лет. Но сначала покажем, что метод не связан обязательно с экзогенным ритмом водителем, и может описывать автономную эволюцию систем.
Еще в шестидесятые годы Т.А. Детлаф экспериментально доказала, и сегодня это это общеизвестно, что вся программа эмбриогенеза холоднокровных животных развивающихся из яйца (насекомых, земноводных и рыб) в качестве кванта времени использует период первичных митотических дроблений яйцеклетки, который может на сотни % изменяться при вариациях температуры окружающей среды, т.е. время вылупление головастиков может плавно меняться от двух недель до месяца, и хотя ни о каком экзогенном, космическом ритме и синхронизации говорить не приходится, но фазы эмбриогенеза выражаются в строгих пропорциях митотических часов. Чтобы не входить в споры об условных определениях фаз эмбриогенеза возьмем безусловные времена, связанные с фазой вылупления или выклевывыния из яйца — концом эмбриогенеза.
Были проанализированы данные по всем животным, описанным в классическом энциклопедическом труде по эмбриогенезу (10). Вот эти результаты в единицах митотического цикла соответствующих животных: прудовик (моллюск) –185; дрозофилла — 127; Пчела — 123-129; морской еж — 127-132; осетр — 120; радужная форель — 248; испанский тритон — 255; оксолоть — 191; шпорцевая лягушка — 115—125; травяная лягушка — 83-92.
Итак мы видим, что 70% животных имеют время продолжительности эмбриогенеза завершающееся в пиках кризиса главного — нулевого порядка, остальные 30% в кризисах первого порядка, в кризисах 2-5 порядков программа эмбриогенеза не финиширует.
Сейчас проводится подробный ритмокаскадный анализ промежуточных фаз эмбриогенеза, и можно утверждать, что теперь удается понять более тонкую структуру процесса.
Очень коротко коснемся средних временных антропологических характеристик. Если принять за единицу времени 1 год, то первые 7 периодов жизни 0-1-3-7-15-31-63-127 на первом уровне графиков вполне отвечают социально обусловленным фазам возрастов человека — младенец, малышь, дошкольник, школьник-подросток, юноша-молодой человек, мужчина, пенсионер-старец. Соответствующие кризисные области отвечают годам максимальной перестройки организма психики и ментальной сферы. При этом уровням по-видимому отвечают типы функциональных систем организма: 1- тканевый, 2- эндокринный -энергетический, 3- эмоциональный.4- рационально- логический (операциональный, причинно-следственный), 5- рационально- интуитивный (творчество), 6 и 7—духовные (о которых мы почти ничего не знаем). Тогда легко интерпретировать развитие детской психики, половое созревание, периоды экзистенциальных кризисов, периоды климакса и максимальной смертности. Отметим, что построенный прямой каскад описывает средний онтогенез мужчины, для женского организма необходимо часть ритмокаскадов обратить.
Видимо разумный максимальный срок отмеренный человеку около 120- 127 лет (последний кризис «0» порядка), хотя выход из трансформационного кризиса происходит в 138 лет, а затем относительно спокойный период до 174 лет –вхождение в новый кризис «1»-порядка 185-190 лет — - переспектива долголетия о которой подозревали геронтологи.
Если же взять за единицу времени 1 сутки, то в культуре так же распространен счет по 3 дня, неделе-7, пол месяца-15, месяцу-31.
Обращаясь к эмбриогенезу человека, следует напомнить хорошо известные в гинекологии факты, что роды с жизнеспособным младенцем возможны начиная с 28 недели = 196 дней — выход из кризиса 1 порядка, центр которого отвечает 5 уровню (высший интеллект), отличающему человека от высокоразвитых животных. Аномальный период, требующий интенсивной терапии младенца заканчивается в 38 недель==266 сут — выход из глубокого кризиса нулевого порядка (248-255), со дна которого так сложно выходить восьмимесячного младенца. После чего в течение 28 дней возможны нормальные роды, этот период относительно спокоен, лишь кризисы 4-5 порядков, он завершается в 294 дня входом в кризис 3 порядка, и тут обычно проводят мероприятия по стимулированию родов.
Ритмокаскадный подход можно применять не только к физиологическим процессам, но и при описании интеллектуальной, психической, творческой деятельности человека и социально-культурным феноменам, на чем мы сейчас не имеем возможности останавливаться.
Одним из основных ритмов Солнечной магнитосферы является ритм т=160 минут = 1/9с =0.1111с. Образуем ритмокаскад с данной частотой, тогда большинство известных суточных ритмов солнечной активности попадают в кризисные зоны ритмокакада старших порядков: 3.5с =31.5 т (мах«0»); 5с=45т (43-46 мах «1»); 7с=63т (мах«0»); 13,5с=121.5т (мин«0»); 21с=189т(185-190 мах«1»); 26-30с = 240 – 270т (тонкая структура старшего кризиса «0» порядка 248-255); 114с=1026т (мах«0»); …… Ряд можно продолжить, но чтобы вычерпать суточные моды солнечной активности следует строить и другие ритмокаскады на базе мультиплета минутных мод активности (6), и периода обращения звезды. В частности так удается объяснить колебания показаний состава крови в зависимости и солнечной активности на языке ритмокаскадов, вполне аналогично тому, как это сделано в (11).
Относительно многолетних мод активности можно предложить ритмокаскад связанный с твердотельной частотой обращения Солнца 28.43 сут., в частности так получаются в главных максимумах известные ритмы около 10 и 20 лет.
Кроме того магнитоплазменная частота 160 мин должна заметно влиять на магнитосферу планет земной группы и проявляться в биосферных ритмах. Так «0» порядки кризисов дают ритмы, с тонкой структурой внутри областей: 1.6с; 3.4с; 7с, 14с, 27-29с; 56-58с; 110-114с; 224-228с; и т.д. А так же кризисы первых порядков, которые получаются примерно симметрично между «0» кризисами, например 85-87с; 340-350с; 680-685с и т.д. Все эти ряды очень напоминают серии Волновой модели А.М.Чечельницкого и зачастую попадают просто на периоды обращения планет земной группы, хотя имеют совершенно иную интерпретацию. И последнее — суточный ритм обращения Земли формирует сложный ритмокаскад в магнитосфере планеты и окружающего пространства, межпланетном магнитном поле. Поэтому вариации потоков космических лучей и другие геофизические показатели должны коррелировать с ритмокаскадом приведенном на графиках, где единицей теперь являются сутки. И действительно, такие ритмы, как: 87, 95, 127, 147, 180, 240, 360, 445, 510, 2775 сут, согласно, графикам попадают либо в пики, либо находятся на границах кризисов главных порядков.
Относительно климатических ритмокаскадных моделей можно предположить наличие ритмокаскада с большими периодами ритмов-водителей, типа прецессии земной оси, и для геологических процессов — галактического года.
В соответствии с нашей гипотезой происхождения спектра эндогенных ритмов Солнечная система должна порождаться деревом ритмокаскадов с общей частотой для всех планет. Таким источником периодической энергии может быть только Солнце, точнее все пространство вокруг него. Для Земной группы планет в качестве ритма водителя можно выбрать период вращения Солнца 27.3 с. (или твердотельный 28.4) либо частоту пульсации «дыхания» Солнца –плазменную магнитогидродинамическую частоту 160 мин. Оказывается, что именно они и организуют ритмокаскад планет земной группы, которые оказываются расположенными у входов или выходов из кризисных резонансных зон старших порядков.
В заключении отметим, что не только сама природа эволюционирует в согласии с принципами гармонии (1,2,3,7), но и механизмы восприятия живыми объектами также проводят «гармоническую» обработку информации (3).
Допустим нелинейная система возбуждена на некоторой частоте, и имеет богатый спектр гармоник, в идеале все обертоны (кратные) и унтертоны (долевые). Основная гипотеза заключается в том, что обработка спектра при восприятии также происходит по принципам ритмокаскадов — здесь сжатия (умножения) спектра последовательно по степеням двойки. На этом принципе предложен новый тип неравномерной музыкальной темперации, названный в (3) каскадной темперацией. Оказалось, что каскадный строй практически объединяет в себе достоинства натурального и хорошо темперированного строя, но обладает и рядом новых качеств дающих основания полагать, что восточная и европейская музыкальные традиции могут быть одновременно адекватно представлены в рамках именно каскадно- темперированного строя.
Отметим так же, что октавный принцип, бесспорно известный пифагорейцам, позволяет трансформировать спектр частот произвольной системы в пределы одной октавы и исследовать его на наличие консонансных и диссонансных интервалов. Именно так могли проанализировать гармоничность солнечной система — «музыку сфер» наши далекие предки. В качестве частот солнечной системы могут быть выбраны либо сидерические (гелиосистема), либо синодические (геосистема) частоты. Можно построить 2 матрицы взаимных отношений любых планет, просто взяв попарные отношения их частот. В работе (3) они исследованы на консонансность и диссонансность, и показана преимущественная гармоничность матриц солнечной системы, а кроме того показано, что гелио- и гео- системы гармонии вполне могли порождать космогоническии мифы о небесном и земном проявлении божественных начал, являясь музыкальным культургенным кодом передачи законов ближнего космоса, порождая изоморфизм символических структур мифа и космо- музыкального языка. Там же, построен ритмо-каскадный образ планетарных частот Солнечной системы в звуковом и цветовом диаппазонах восприятия. Таким образом, впервые удалось получить не психофизиологическую, субъективную окраску звуков, но связать высоту звука и цвет сквозным каскадным синхронизмом.
Все эти неслучайные случайности свидетельствую о том, что октавный принцип, ЗС, ритмокаскады соединяют воедино не только локальные доступные нашему наблюдению области, но пронизывают реальность на значительно больших пространственно-временных масштабах. Когда промежуточные эволюционные звенья уже не существуют, они наследуют коммуникационные коды и обеспечивают «узнавание» реальности и конструктивного диалога с ней. Возможно таков нерефлексируемый механизм интуиции, информационный канал работающий по методу гомологических рядов, аналогии, символов. Быть может гармония и есть основной проводник антропного принципа? В экологической проблематике это сулит новый подход к технологиям коэволюции с природой, «технологиям гармонии» не в метафорическом, но буквальном мысле. Сегодня это новая исследовательская программа.
Метод ритмокаскадов, предложенный в (3,4), также имеет более широкий, самостоятельный междисциплинарнй статус. Фактически рассматривается проблема самоорганизации времени в сложных иерархических эволюционирующих системах, как природных, так и человекомерных. На основе современных синергетичесих представлений об универсальных структурно-порождающих механизмах в динамическом хаосе предложен метод ритмокаскадов, дополняющий широко известные идеи линейного ритма нелинейными механизмами его коэволюции в системе. В таком подходе гармонический экзогенный или эндогенный ритм- водитель начинает последовательно «прорабатывать» разные уровни системы, создавая иллюзию лакун — его исчезновения на некоторое время, а затем возрождения на данном уровне системы. Ритм начинает носить прерывистый характер, что и позволяет вводить интерпретацию разных фаз жизни систем, да и самого времени жизни. Кроме того, ритм-водитель по мере развития системы порождает все большее множество других ритмов.
Крайне важно, что ритмокаскадная эволюционная программа развития системы моделируется временным фракталом. Именно в самоорганизующихся сложных системах структуры в присутствии хаоса имеют фрактальную природу (13). Например, временные ряды кардиограмм и энцифолограмм помимо синусоидального ритма и шума несут ярко выраженную фрактальную компоненту свидетельствующую об этих структурах. Таким образом не бесконечные гармонические циклы, которыми так все увлечены, но фрактальные временные ряды станут в ближайшее время основными поставщиками содержательной информации об эволюционирующих и живых системах.
В работе (14) показано, что временная фрактальность процессов является универсальным свойством систем, обладающих структурной иерархией доступа к обобщенному ресурсу, который может иметь любую природу: информация, энергия, вещество и т.д.. При этом максимальная скорость фрактального роста, максимальный темп эволюции системы именно у ритмокаскадного фрактала (*). По-видимому он оптимален для природных развивающихся систем.
Итак, поле приложений метода: закономерности организации Солнечной системы, ритмов ближнего космоса и биосферы; фазы эмбриогенеза животных и развиния биоценозов; онтогенеза человека; исторические и социально- экономические закономерности, генезис принципов музыкальной гармонии, и т.д.
Относительно биосферных задач, сохранения и управления процессами биосферы, отметим, что ритмокаскадная эндогенная идеология более автономна, она указывает вполне конкретный источник широкого спектра биосферных ритмов, что может позволить компенсируя его влияние согласованно менять все дерево ритмокаскадов. Теперь мы можем надеяться на понимание причинноследственных связей, а не просто корреляций, что в конечном счете необходимо для грамотного моделирования и прогноза биосферных процессов.
Буданов В.Г. Метод ритмокаскадов: о фрактальной природе времени эволюционирующих систем // «Академия Тринитаризма», М.,Эл № 77-6567, публ.11356, 20.07.2004
[Обсуждение на форуме «ИНЕ»]
Буданов В.Г.
Метод ритмокаскадов:
о фрактальной природе времени
эволюционирующих систем
о фрактальной природе времени
эволюционирующих систем
В работе рассматривается проблема самоорганизации времени в сложных иерархических эволюционирующих системах, как природных, так и человекомерных. На основе современных синергетичесих представлений об универсальных структурно-порождающих механизмах в динамическом хаосе предложен оригинальный метод ритмокаскадов, дополняющий широко известные идеи линейного ритма нелинейными механизмами его коэволюции в системе. В таком подходе гармонический экзогенный или эндогенный ритм-водитель начинает последовательно «прорабатывать» разные уровни системы, создавая иллюзию лакун — его исчезновения на некоторое время, а затем возрождения на данном уровне системы. Ритм начинает носить прерывистый характер, что и позволяет вводить интерпретацию разных фаз жизни систем, да и самого времени жизни.Кроме того, ритм-водитель по мере развития системы порождает все большее множество других ритмов. В качестве иллюстрации метода рассмотрены закономерности организации Солнечной системы и ритмов ближнего космоса и биосферы; фазы эмбриогенеза животных и онтогенеза человека; а также возможный генезис принципов музыкальной гармонии.
ОСНОВНАЯ ИДЕЯ
ЗОЛОТОЕ СЕЧЕНИЕ — ВОЛНА РЕЗОНАНСОВ
МЕТОД РИТМОКАСКАДОВ
Основные постулаты:
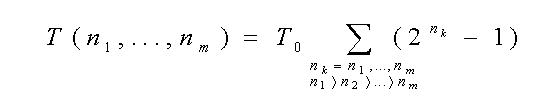
СВОЙСТВА ДЕРЕВА ПРЯМЫХ РИТМОКАСКАДОВ

|
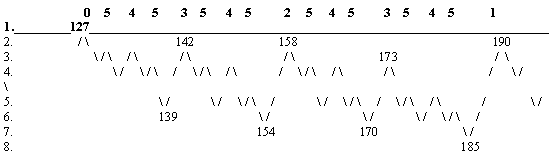
|
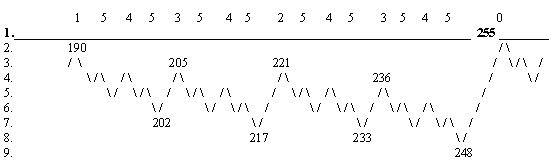
|
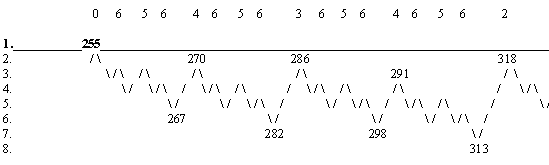
|
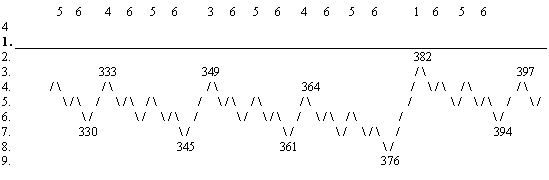
|

|
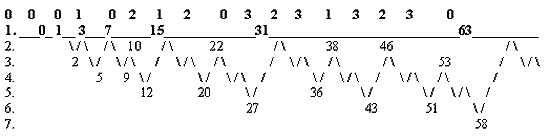
|

ПРИЛОЖЕНИЯ МЕТОДА РИТМОКАСКАДОВ
ВРЕМЯ ЭМБРИОГЕНЕЗА ХОЛОДНОКРОВНЫХ ЖИВОТНЫХ
ОНТОГЕНЕЗ ЧЕЛОВЕКА
РИТМЫ СОЛНЕЧНОЙ АКТИВНОСТИ
РИТМЫ БИОСФЕРЫ
ПЛАНЕТАРНЫЕ ОРБИТЫ
О ПРИРОДЕ ЭВОЛЮЦИОННЫХ СИНХРОНИЗМОВ И ПРИНЦИПОВ ГАРМОНИИ
ФРАКТАЛЬНОСТЬ ЭВОЛЮЦИОННОГО ВРЕМЕНИ
- И.Ш.Шевелев, М.А. Марутаев, И.П. Шмелев. «Золотое сечение. Три взгляда на природу гармонии». Москва. Стройиздат. 1990. 342 с.
- К.П. Бутусов «Золотое сечение в Солнечной системе». АН СССР. Астрометрия и небесная механика. Серия: Проблемы исследования Вселенной. Вып.7, Москва-Ленинград 1978, с.475- 500.
- Буданов В.Г. «Принципы гармонии как эволюционные синхронизмы — начала демистификации». Труды международной конференции «Математика и искусство» Суздаль -- 1996. Москва, изд. «Прогресс -традиция» 1997, с.116-122.
- Буданов В.Г. «Синергетика ритмокаскадов в эволюционирующих системах». Труды юбилейной сессии РАЕН — «Леонардо Да Винчи ХХ века. К 100 — летию А.Л.Чижевского». 27- 28 февраля 1997. Москва 1997.
- Чечельницкий А.М. «Волновая структура Солнечной системы и ритмы биосферы» Современные проблемы сохранения и изучения биосферы, Т.1. Свойства биосферы и ее внешние связи. Санкт-Петербург, Гидрометиздат 1992.
- Васильева Н.И. «Моделирование природных периодических процессов с помощью системы гармонических волн». Материалы IY Международной конференции «Циклы природы и общества». Издательство Ставрапольского университета, г. Ставраполь, 1996. с. 36--59.
- Аршинов В.И., Буданов В.Г.. «Синергетика — эволюционный аспект».В книге «Самоорганизация и наука: опыт философского осмысления» ИФ РАН, Арго, 1994.
- Хакен Г. Синергетика. Динамика иерархических структур
- Шарковский А.Н. Украин. Мат. Журн. 1964-т.16.-с.61.
- Объекты биологии развития. Москва. Наука. !989. с. 580.
- Чиркова Э.Н., Суслов Л.С., Клюева З.П., Нечитайло О.А., Захаренко А.В. «Согласование внутригодовых ритмов изменений концентрации гемоглобина крови человека с космическими ритмами». Современные проблемы изучения и сохранения биосферы. II. Живые системы под внешним воздействием. РАН. Санкт-Петербуг Гидрометеоиздат 1992. С. 440.
- Шустер Э. Детерменированный хаос. Мир. 1987.
- Федер А. Фракталы. М. Мир. 1990.
- Буданов В.Г. Временная фрактальность в задачах с приоритетами. Ритмокаскады иерархических систем. Проблемы теоретической биофизики. Международная школа МГУ. 1998.
Буданов В.Г. Метод ритмокаскадов: о фрактальной природе времени эволюционирующих систем // «Академия Тринитаризма», М.,
|
|