Японская храмовая геометрия (сангаку – математическая дощечка) [1–4] – математические таблички и геометрические головоломки, выгравированные на расписных деревянных дощечках в эпоху Эдо (1603–1868). Обычно размещались в храмах, принося задачу в дар богам и одновременно бросая публичный вызов своим коллегам.

Страна была в полной самоизоляции. О трудах европейских ученых не знали.

Решали сангаку с помощью простой математики, и в настоящее время они больше представляет уникальное культурное достояние-наследие, объединившее в себе науку, искусство и религию, и содержат сильное эстетическое начало.

Если древние греки стремились через геометрию проникнуть во вселенские первоначала и объяснить мироустройство, то японцы больше наблюдали за явлениями этого мира, созерцали, любовались. Необыкновенное чувство формы и восприятие природной красоты нашло отражение в их самобытной геометрии.

Любопытный момент. Японские геометры, получив китайский перевод Начал Евклида, были сильно удивлены чрезмерной скрупулезностью и исключительной строгостью рассуждений, которыми действительно изобилуют древнегреческие трактаты. Зачем, – сказали они, – доказывать такие очевидные факты, когда есть ещё много красивых и сложных геометрических теорем [1].

Плюс к этому несомненное удовольствие от визуального наблюдения и особенной гармонии с повышенным вниманием к окружностям и эллипсам (рис. 1). Вторая задача имеет даже собственное имя – "хвост павлина" (1865): большая желтая окружность, в неё вписаны две оранжевые, которые охвачены дугами радиусом желтой с образованием зеленых фигур, далее вписаны 4 одинаковые красные окружности и 4 синие [5].

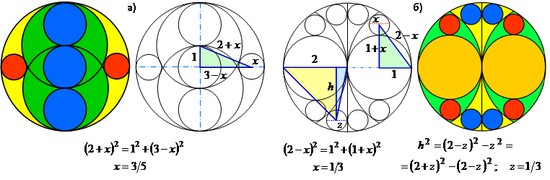
Рис. 1. Примеры сангаку: на дощечках приводились только цветные картинки и условие задачи:

а) найти радиус красного круга; б) доказать равенство красных и синих кругов.

К слову, задача о трех окружностях [6] взята из сангаку [1]. Она решалась с использованием теоремы Пифагора и ряда алгебраических преобразований.

Но можно иначе, методом подобия и последующим составлением математической пропорции. Ближе к евклидовой геометрии. Такой подход выглядит более элегантно, отвечает общему принципу пространственной организации природных объектов и получил развитие в японской математике. Не случайно японская система образования в начальной и средней школе считается одной из лучших в мире – второй после Финляндии.

формате PDF (1216Кб)