Дискуссии - Наука

С.Л. Василенко

Аннотация. Введено новое понятие: комплексная золотая пропорция (ЗП) – решение золотой пропорции на комплексной плоскости с использованием противоположных чисел, адекватных философской категории отрицания. Единая дуальная ЗП воспроизводится корнями квадратичного полинома x² ± x ± 1 и замыкает на себя все правильные тела Платона. Действительная ЗП (1 ± √5)/2 с осевой симметрией пятого порядка, как модель роста и геометрическая прогрессия с дополнительным аддитивным свойством, характеризует живые системы. Комплексная ЗП (1 ± i√3)/2 характерна для неживых (костных) систем с треугольной и гексагональной структурой.

Комплексные числа – это прекрасное и чудесное убежище

божественного духа, почти что амфибия бытия с небытием.

Г.В.Лейбниц

Введение в тему.

Тему золотой пропорции (золотого сечения) не описывал или не упоминал разве что ленивый, невежда или надменный, начиная от школьников средних лет до седовласых академиков. Объект, что называется на виду, с отчетливыми проявлениями.

Математики считают его слишком простым и очевидным. Физики обходят стороной. Биологи довольствуются проявлениями филлотаксиса в строении живых образований. Философы иногда используют, подвергая "экзекуции" понятие целого.

Многие специалисты находят нечто похожее на золотое сечение в разных областях и процессах. Хотя достоверность обнаруживаемого явления всегда остается под большим вопросом, особенно в костных системах, ибо доказательная база очень слабая. Неизвестно что они там находят, проявление именно какой числовой закономерностей. Только догадки, предложения, гипотетические раскладки и подгонки.

Мы практически не встречаем золотого сечения в неживых процессах, явлениях и объектах. Оно им не свойственно по природе.

Ну, с каких таких дел? – Если осевая симметрия пятого порядка определяет один единственный (!) центр, без дальнего порядка. Подобно аморфным телам.

Поэтому напрасны потуги его обнаружения в кристаллических решетках, в которых на пятый порядок наложено табу.

И наоборот, золотая пропорция – это системный признак живых объектов. Основа модели их роста, развития, внутреннего устройства. Генезис пятого порядка с единым центром вращательной симметрии начинается с материнской клетки и генерирует процесс деления, образующий мягкие эластичные формы, не дающие живому закостенеть.

С точки зрения стороннего наблюдателя живые объекты сходны с не живыми: имеют объем, движутся, образуют кластеры (социальные группы городов) и т.п.

Но эта сторона медали, а именно общности живого и неживого, как-то остается в стороне. Мы зациклились на видимой точке золотого сечения геометрического отрезка, и дальше не видим. Либо не хотим видеть или не умеем. Разве что составлять пропорцию «целое – к большему, как большее – к меньшему» на все лады и в любых сферах.

Как геометрия Евклида. Всем она замечательна. Многие задачи решает вполне успешно. Решает гибко, эффектно, элегантно. Но с ней не выйдешь на микро-уровни элементарных частиц или макро-просторы Вселенной с искривленным пространством, где без геометрий Лобачевского, Римана просто не обойтись.

В тематике золотой пропорции сложилась похожая ситуация. Специалисты усердно продолжают выискивать наличие-проявление действительной иррациональной константы золотого сечения Ф = ф^–1 ≈ 1,618 в неживых процессах и явлениях, которой там нет.

Практически по определению, по своей сути, a priori.

Ближе к постановке задачи.

В абсолютной точности величины Ф = (1+√5)/2 одновременно заключена сила и слабость. Слабость вытекает из крайне ограниченного круга задач, где золотая пропорция проявляет себя в явном виде. Остальные исследования в этой области построены исключительно на гипотетических предположениях, чаще никак не обоснованных. Из чистого желания получить вожделенное значение, хоть чем-то напоминающее константу золотого сечения Ф. Ну, хотя бы 2–3 похожие цифры. Не сравнивали разве что нос ежа и хвост ужа, – для изготовления золотой колючей проволоки.

Ларчик открывается просто. Люди, весьма отдаленные от математики, западают на простоту и элегантность "золотой модели". Большого ума и специальной подготовки не надо. Формы просты и наглядны. Бери любую тему с несимметричным отношением. Сиди себе и складывай, или умножай, либо дели. Что делить? – Да, хоть что. Корову, планеты, стихи, картины... Проводят линии квазиЗС или псевдоЗС [1] и безмерно радуются.

Гипертрофированная одержимость идеей о всеобщей гармонизации мира исключительно на основе обычной золотой пропорции наносила и продолжает наносить вред установлению её действительной роли в мироздании.

Не случайно, на протяжении более двух тысячелетий интерес к золотой пропорции не раз менялся на противоположный знак. Наука надолго отворачивалась от числа Ф до следующей сенсации, как правило, броской, эффектно поданной, но в итоге малосодержательной по своей сути.

А что если противоположный знак нужно менять не в субъективном мнении-отношении к уникальной математической константе Ф? – Но изначально его заложить в саму суть формирования золотой пропорции.

Может в этом и состоит то самое главное – "зри в корень", которое совсем рядом.

Мы постоянно через него переступаем, но не замечаем.

Находим проявления пятого порядка в формообразовании живых структур, но не можем вразумительно объяснить их сходство с неживыми системами в контексте физических характеристик движения, объема, внутреннего строения костей и др.

Итак, попытаемся начать с самого сначала, с азов, ab origine…

Вещественная ЗП.

Рассмотрим целостный объект, условно принятый за единицу и состоящий из двух аддитивных частей. Для наглядности можно выбрать единичный геометрический отрезок.

1) Пусть b – <большая> часть целого.

Пропорция, характеристическое уравнение с решением и возвратное уравнение:

(1+b)/1 = 1/b = b/(1–b);

b² = 1 – b = 0, b_1,2 = (–1 ± √5)/2 = (–Ф, ф);

f_n+1 = f_n–1 – f_n.

Итерационный процесс, начиная с (f₀, f₁) = (0, 1), приводит к знакопеременному ряду чисел Фибоначчи с их аттрактором (предельным отношением) A = –Ф, который определяет деление целого внешним образом. Аттрактор является свойством рекурсии, поэтому в общем случае не зависит от выбора начальных условий.

То же самое на языке геометрической прогрессии 1, q, q²:

q² = 1 – q → геометрическая прогрессия, наделенная вычитанием;

q = b₂ = –Ф → возрастающая знакопеременная последовательность;

q = b₁ = ф → убывающая последовательность положительных чисел.

Величина q² в геометрической прогрессии – не просто число, умноженное само на себя. Это геометрическая фигура квадрата, построенного на отрезке, ассоциированном с числом q.

2) Пусть x >1 – отношение частей целого.

Пропорция, характеристическое уравнение с решением и возвратное уравнение:

(1+x)/x = x/1 = 1/(x–1);

x² = 1 + x = 0, x₁₂ = (1 ± √5)/2 = (–ф, Ф);

f_n+1 = f_n–1 + f_n.

Итерационный процесс для (f₀, f₁) = (0, 1) приводит к числам Фибоначчи с аттрактором A = Ф, то есть делению целого внутренним образом.

Альтернативное представление в числах 1, q, q²:

q² = 1 + q – геометрическая прогрессия, наделенная сложением;

q = x₂ = Ф → возрастающая последовательность положительных чисел;

q = x₁ = –ф → убывающая знакопеременная последовательность.

Объединенные уравнения по пунктам 1 и 2 (характеристическое и возвратное):

x² = 1 ± x, f_n+1 = f_n–1 ± f_n, A = ±Ф.

Знак минус и отрицание.

Для дальнейшего изложения напомним некоторые аспекты, связанные с применением знака минус.

В современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом "минус", хотя алгебраически это разные понятия.

Знак минус выступает в двух значениях: как вычитание и как признак числа, противоположного заданному числу.

Два числа называются противоположными, если их арифметическое сложение дает ноль. Такие числа имеют одинаковые модули, но противоположные знаки, то есть они отличаются только знаком. Противоположное число для v обозначается –v.

Если перед переменной стоит знак минус, например –v, это не значит, что данная величина отрицательна. Знак означает, что данная величина противоположна числу v. Какое из них положительное и какое отрицательное, мы заранее не знаем.

Умножение и деление чисел с противоположными знаками дает минус.

Отрицание следует понимать диалектически, отличая обыденного его понимания, как простого уничтожения и/или отбрасывания. В философии Гегеля такое состояние характеризует понятие "снятие" или момент развития, соединяющий как отрицание, так и сохранение, утверждение. Развивающийся объект становится иным и одновременно в определенном смысле остается тем же самым с сохранением преемственности и удержанием существенных составляющих. Что в полной мере воспроизводится математически на комплексной плоскости на языке мнимых величин.

Формальное отрицание характерно для научного дискурсивного мышления, связных логических рассуждений на основе дедукции–индукции с формированием умозаключений.

В математической логике отрицание есть функтор истинности, ибо значение отрицаемого истинного высказывания есть ложь, а значение отрицаемого ложного высказывания есть истина, о каком бы высказывании ни шла речь, и что бы оно ни означало [2, § 25].

Бог – отрицание предиката квантора всеобщности, или «сущий над всем» (Рим. 9:5).

Долгое время отрицательные числа называли ложными, мнимыми, абсурдными.

Даже в XVII веке Паскаль считал, что 0 – 4 = 0, так как ничто не может быть меньше, чем ничто. Приводили также странную пропорцию 1:(–1) = (–1):(1), в которой первый член слева больше второго, а справа – наоборот, и получалось, что большее равно меньшему (парадокс Арно). Гаусс разъяснял (1831), что отрицательные числа принципиально имеют те же права, что и положительные. А то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам, например, неприменимы при счете людей.

Интуиция подсказывает, что вводимую ниже комплексную золотую пропорцию ждет нечто подобное. С возможным развитием ситуации: от недопонимания и/или непризнания до приобретения "прав гражданства". Время покажет и рассудит. – Tempus consilium dabet.

Но всё по порядку…

Постановка задачи о комплексной золотой пропорции.

Определение. Комплексная золотая пропорция: целое так относится к части, выражаемой числом, как её противоположность относится к другой части.

Или в широкой формулировке: целое так относится к числу, выражающему часть целого, как противоположное этому числу относится к числу, выражающему другую часть.

Можно кратко, по сути главного: целое – к части, как её "отрицание" – к другой части.

Эквивалентная форма, вытекающая из свойств любой пропорции: целое – к части, как она – к противоположности (отрицанию) другой части.

Проследим, что из этого получается. И почему именно комплексная пропорция.

Комплексная ЗП.

3) Пусть x – отличная от половины часть целого. Составим пропорцию: целое – к части, как её противоположность (отрицание) – к другой части:

1 / x = –x / (1 – x) = (1 – x) / 1.

Характеристическое уравнение с комплексным решением и возвратное уравнение:

x² = x – 1, x₁₂ = (1 ± i√3)/2;

f_n+1 = f_n – f_n–1.

Величина i – мнимая единица такая, что i ² = –1. Мнимая только потому, что не существует вещественного числа c, для которого c² = –1.

Рекурсия, согласно разностному уравнению, образует циклично-повторяющуюся последовательность D = (f₀, f₁, –f₀+f₁, –f₀, –f₁, f₀–f₁).

Например, D = (1, 1, 0, –1, –1, 0), как прототип шестиугольника.

Движение в рекуррентной последовательности напоминает циклические колебания в 6-угольнике "силовых линий" без четко выраженного аттрактора.

4) Пусть x – отношение частей. Составим пропорцию с отрицанием

(1 + x) / x = –x / 1 = 1 / (1 + x).

Характеристическое уравнение с комплексным решением и возвратное уравнение:

x² = –x – 1, x₁₂ = (–1 ± i√3)/2;

f_n+1 = –f_n – f_n–1.

Рекурсия, согласно разностному уравнению, образует циклическую последовательность T = (f₀, f₁, –f₀–f₁). Например, T = (1, 1, –2), как прототип треугольника.

То есть в рекуррентной последовательности дискретное движение становится циклическим колебанием в структуре треугольной формы без определенного аттрактора.

Комплексация – не порок.

Могут спросить, для чего нужны эти "невозможные" решения – комплексные корни.

Ответим, прежде всего, словами А.Жирара, который отмечал три причины: для незыблемости общих правил, чтобы не было других решений и по причине их полезности.

Тем более что корни «хорошо прописываются и уютно живут» на комплексной плоскости [3] – евклидовой плоскости в системе ортонормированных координат с базисными векторами (1, i ), i ² = –1.

Что может означать противоположная или отрицательная часть в комплексной золотой пропорции? – Прежде всего, взаимодействие с внешней средой относительно целого. Подобно тому, как отрицательные корни-решения для единичного отрезка означают точки золотого деления за пределами самого отрезка.

Здесь похожая ситуация, только отрицательность закладывается априори на уровне исходной пропорции и означает разные ситуации: поступление информации извне и её переработка, обмен энергией с возможным изменением энтропии и т.д.

Как видно, комплексное золотое сечение введено нами аналогично вещественному аналогу, только через "отрицание" или противоположность сравниваемой части целого.

Объединение пунктов 1–4 дает общую формообразующую структуру единого (общего) комплексно-дуального золотого сечения: 2·(ф, Ф, ф', Ф') = ± 1 ± √(1 ± 4).

Объединенные уравнения (характеристическое и возвратное):

x² ± x ± 1, f_n+1 = ± f_n ± f_n–1.

Сопутствующие уравнения и пропорции.

Двучленно-аддитивная рекурсия f_n+1 = f_n + f_n–1, как возвратное уравнение и разностный аналог характеристического уравнения x² – x – 1 = 0 классической золотой пропорции (1 + x)/1 = 1/x или 1/x = x/(1 – x) с равными средними членами, допускает дискретно-временную интерпретацию параметра n и соответствующие условно-символьные представления [4]:

«будущее = настоящее + прошлое»; «завтра = сегодня + вчера».

Составляющие перманентной структуры «вчера – сегодня – завтра» имеют общий масштаб и равносильны, то есть берутся с одинаковыми весами или пропорциональными коэффициентами 1.

Такая модель удобна и полезна для сравнения различных алгебраических триномов x^r – px^s – q без выполнения геометрических построений, сложность которых существенно растет при введении дополнительных коэффициентов p, q и увеличения степеней r, s.

Более того, с ростом степеней r, s становится невозможным не только геометрическое построение, но и аналитическое нахождение корней полиномов.

Остается только графическая визуализация и численное решение на ЭВМ.

1) Характеристическое уравнение x² – x – 1/2 = 0 двучленно-аддитивной рекурсии с ослабленным прошлым f_n+1 = f_n + f_n–1/2 – «будущее = настоящее + (1/2) прошлого».

Пропорция 1/x = x/(x + 1/2) – модель роста относительно середины целого, а не всего целого, как в обычной золотой пропорции.

Решение x_1,2 = (1 ± √3)/2, как отображение комплексной золотой пропорции на действительные числа. Положительный аттрактор равен (1 + √3)/2 ≈ 1,366.

В словесно-описательной форме, это модель, не отягощенная чрезмерно прошлым. Ближе к реформаторскому обновлению. Прошлый опыт учитывается, но ставка больше делается на свежий, более сильный потенциал.

Своего рода концептуальная формула: «молодым – дорога, старикам – почет».

Разложения в бесконечную цепную дробь похожи: √3 = [1; 1, 2], (1+√3)/2 = [1; 2, 1], отличие в перестановке периода.

2) Характеристическое уравнение x² – 2x – 2 = 0 двучленно-аддитивной рекурсии с коэффициентом усиления f_n+1 = 2f_n + 2f_n–1 – «будущее = 2·настоящее + 2·прошлое».

Пропорция 1/x = x/(2x + 2) – модель удвоенного ускоренного роста: a_n = 1, 1, 4, 10, 28, 76, 208, 568, ... Рекурсия не удваивает числа Фибоначчи и приводит к последовательности с аттрактором 1+√3 ≈ 2,732, который перекликается с комплексной ЗП.

Альтернативное получение ряда: a_n/b_n = 1/1, a_n+1/b_n+1 = (a_n + 3b_n) / (a_n + b_n).

3) Характеристическое уравнение x² – 2x + 4 = 0 двучленно-аддитивной рекурсии f_n+1 = 2f_n – 4f_n–1 с комплексными корнями x_1,2 = 1 ± i √3.

Образуется знакопеременная последовательность a_n = 1, 1, –2, –8, 8, 16, 64, 64, –128, –512, –512, 1024, 4096, 4096, – 8192, ... которая состоит из степеней двойки без аттрактора с периодическим изменением отношений соседних членов, равных T = (1, –2, 4) в треугольнике "силовых линий".

Имеет место похожесть на численное удвоение в комплексной ЗП. Но одновременно присутствует явный рост чисел, хотя и с периодическим изменением знаков. Тройственность, выраженная корнем √3, проявляется через три периодических отношения соседних чисел последовательности. Возможно, в этом и состоит специфика масштабирования комплексных корней: (1 ± i √3)/2 → 1 ± i √3.

Кроме того, a_n = –8·a_n–3, а также a_n = 2ⁿcos(n·π/3).

4) Характеристическое уравнение x² – x + 3/2 = 0 двучленно-аддитивной рекурсии f_n+1 = f_n – 3/2·f_n–1 с комплексными корнями x_1,2 = (1 ± i √5)/2.

Весьма любопытная модель. Своего рода "калька" золотого сечения на комплексную плоскость. Формирует знакопеременную бесконечно возрастающую последовательность.

В зависимости от начальных условий образуется 6 троек чисел одного знака, потом 8 троек чисел другого знака. Все эти тройки разделяются последовательными двойками и тройками чисел противоположного знака.

Период составляет 6·3 + 8·3 + (2 + 3)·6 = 2³·3² = 72.

Число 72 имеет особые свойства, такие как:

– сумма четырех последовательных простых чисел 13 + 17 + 19 + 23,

– сумма шести последовательных простых чисел 5 + 7 + 11 + 13 + 17 + 19;

– наименьшее число, пятая степень которого представляет собой сумму пяти меньших пятых степеней: 72⁵ = 19⁵ + 43⁵ + 46⁵ + 47⁵ + 67⁵;

– пятая часть полного угла 360⁰ и внешний угол правильного пятиугольника на плоскости, в градусах;

– сумма значений функции Эйлера φ(x) первых 3·5 = 15 целых чисел;

– высокоточное число, имеет 17 решений уравнения φ(x) = k = 72, больше чем любое предыдущее k;

– максимальное число сфер, касающихся одной сферы в плотной упаковке в 6-мерном пространстве;

– сумма кубов двух натуральных чисел 2³ + 4³.

Создается впечатление, что исходная модель не может до конца определиться и мечется между 3, 5 и 6 порядками, больше всё-таки тяготея к третьему порядку. Что в целом хорошо корреспондируется с комплексной золотой пропорцией.

Кроме того, в подкольце целых алгебраических чисел (комплексных корней многочленов с целыми коэффициентами) вида a + b√(–5) имеют место 2 разложения (Куммер): 6 = 2·3 = [1 + √(–5)]·[1 + √(–5)].

Невозможное становится возможным

Рассмотрим целое 1, состоящее из двух частей 1 = x + (1 – x).

Из трех величин 1, x, 1 – x допустимо составить шесть отношений:

1/x, x/1, 1/(1 – x), (1 – x)/1, x/(1 – x), (1 – x)/x.

Их этих отношений можно скомбинировать C₆² = 6·5/2 = 15 математических пропорций с возможными решениями:

x = 0, x = 1 – целое совпадает с одной частью, второй части нет;

x = 1/2 – деление целого пополам;

x = 2 в пропорции 1/(1 – x) = (1 – x)/1 или 1/(–1) = (–1)/1, что приводит к тождественному равенству двух отрицательных единиц (см. "парадокс" Арно);

x_1,2 = (–Ф, ф) – золотое сечение, где (–Ф) – соответствует делению внешним образом;

x_1,2 = (ф², Ф²) – золотое сечение, где Ф² – соответствует делению внешним образом;

x_1,2 = (1 ± i √3)/2 – комплексные решения пропорции 1/x = (1 – x)/1.

Таким образом, имеем деление целого пополам, два внутренних симметричных золотых сечения x = ф и x = ф² таких, что ф + ф² = 1, дополненных точками внешнего деления, и одно решение в области комплексных чисел.

Последнее решение вытекает из, казалось бы, невозможной пропорции 1/x = (1 – x)/1: <большее единицы> отношение целого к части равно <меньшему единицы> отношению другой части к целому. Но это только в действительных числах. В области комплексных чисел пропорция верна.

Возникает вопрос, к чему "приткнуть-пристегнуть" эту пропорцию? – Для ответа внесем альтернативное построение, заменив часть (1 – x) на её противоположность (x – 1) или 1/x = (x – 1)/1, откуда следует x_1,2 = (–ф, Ф), то есть золотое сечение с отрицательным значением –ф. Оно и понятно, поскольку пропорция составлена с использованием противоположных чисел.

Таким образом, комплексные решения x_1,2 = (1 ± i √3)/2 характеризуют не что иное, как золотое сечение, основанное на пропорциональном сопоставлении противоположных чисел, выражающих одну из частей целого.

Невозможное становится возможным, если выбраться из пут действительных чисел и перейти к более общему понятию комплексных аналогов, а части целого представлять в виде взаимодействующих противоположностей, с присвоением разных знаков.

Итак, имеем: деление пополам, золотое сечение и комплексную пропорцию. Как единый целостный объект, состоящий из двух взаимосвязанных частей.

Отрицание в золотой пропорции.

В формализованном языке логики отрицание – унарная операция, с одним входом – операндом.

Если в модели действительной ЗП применить двойное отрицание 1 / x = –x / (–1 + x), то приходим к обычному золотому сечению 1 / x = x / (1 – x). То есть само по себе отрицание вполне допустима операция. Причем двойное отрицание приводит к положительному утверждению и действительным корням. Что вполне естественно и отвечает диалектическому закону «отрицание отрицания» и общим правилам алгебры логики (алгебры высказываний) согласно принципу снятия двойного отрицания.

Отрицание, формируемое с помощью противоположных чисел, переводит решение золотой пропорции в комплексную плоскость. На генетическом уровне первопричин, точно такое же полноправное решение. К нему нужно только привыкнуть и правильно использовать. Решения находятся на единичной окружности |z| = 1.

Четыре точки комплексной ЗП вместе с точками вещественной оси ±1 образуют вершины правильного шестиугольника.

Физика и лирика комплексной ЗП.

В понятие противоположности мы вкладываем разные смыслы: белое – черное, левое – правое, ин-янь, меньшее – большее и т.п.

В математике противоположные числа равны по модулю и имеют противоположные знаки. Как сказано выше, выражение "–v" не означает, что перед нами обязательно отрицательное число, поскольку значение v может быть меньше нуля.

В обычном золотом сечении на положительной вещественной полуоси мы сравниваем две противоположности «меньшее – большее», которые в сумме дают целое, принятое за единицу 1.

Ничто нам не мешает составить аналогичную пропорцию в системе противоположных чисел на всей координатной оси: целое относится к части, как её числовая противоположность – к другой части: 1 / x = (–x) / (1 – x). Откуда x_1,2 = (1 ± i √3) / 2.

Распространенный способ построения пентагона в заданной окружности предложил Клавдий Птолемей в 10 главе 1 книги своего трактата по небесной механике "Альмагест".

Вначале проводятся две одинаковые окружности для нахождения середины радиуса, что, по сути, представляет построение комплексной ЗП и прообраз правильного шестиугольника. То есть сначала находится решение комплексной ЗП, а уже потом через гипотенузу прямоугольника 1×1/2 воспроизводится вещественное (действительное) золотое сечение.

Отсюда следует простое построение комплексного и действительного золотого сечения (см. рисунок).

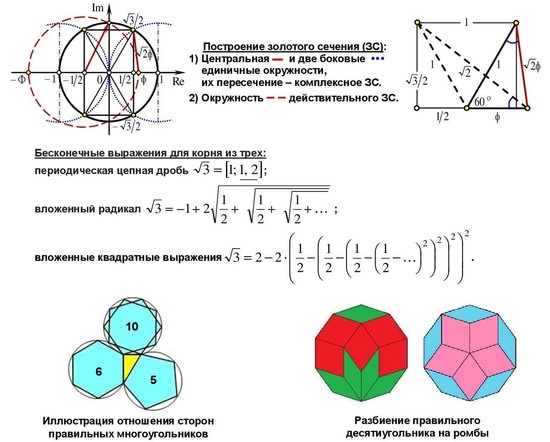
Причем решение комплексной ЗП находится первым, как графическое решение пересечения двух окружностей на комплексной плоскости:

а) x² + y² = 1 и (x – 1)² + y² = 1 → (x, y) = (1/2, ±√3/2);

б) x² + y² = 1 и (x + 1)² + y² = 1 → (x, y) = (–1/2, ±√3/2).

И только после соединения точек с фиксацией середины радиуса единичной окружности проводится окружность действительного золотого сечения. Без предварительного деления единичного отрезка пополам никак не обойтись.

В этом видится своеобразный символизм и специфика организации процесса образования:

– комплексная золотая пропорция (КЗП) с квадратным корнем из трех √3 отражает костные нежизненные формы-структуры и общие объемные характеристики живых образований;

– действительная золотая пропорция (ДЗП) с квадратным корнем из пяти √5 требует дополнительной операции по «вживлению духа» для синтеза фундаментальной матрицы живого биологического объекта, которая характеризует систему пятого порядка с единым центром осевой вращательной симметрии.

Длина окружности, вписанной в прямоугольник, численно равна π. Имея 1 и 1/2, легко находим константы ф, Ф. Перед нами деление пополам, действительное и комплексное золотое сечение, то есть налицо отражение всех золотоносных пропорций.

Уравнения ДЗП x² = 1 ± x, уравнение КЗП x² = –1 ± x . Вместе они составляют единую (общую, совокупную) дуальную золотую пропорцию.

По сути, это составляющие «фундаментального кода природы» (С.Якушко) или архитектурные кирпичики: ДЗП – живых объектов, КЗП – костных объектов.

Комплексные золотые треугольники.

Модуль комплексного корня КЗП равен |z| = 1.

Прямоугольник 1×√3, образованный точками комплексной ЗП, по сути, построен на стороне квадрата 1×1 и его диагонали (√3)² = 1² + (√2)². Диагонали прямоугольника равны 2 и расположены под углом наклона tg β = √3 или β = 60⁰.

В некотором смысле этот обобщение золотого сечения или его расширение на комплексную область. Появляются равновеликие золотые треугольники [5] с соотношением двух сторон 1:ф, в которых третья сторона выступает дополнительной степенью свободы (см. рисунок):

– остроугольный (ф, ф√2, 1) с соотношением сторон (1: √ 2 : Ф) ≈ (1 : 1,414 : 1,618), углом 60⁰ и высотой √3/2;

– тупоугольный (ф, 1, √2) с углом 120⁰, длинная сторона которого =√2, высота =√3/2.

Относительно единичной меры данные золотые треугольники объединяют три размерных, но несоизмеримых ключевых радикала √2, √3 и √5 = ф + Ф, характерных для "великолепной пятерки" платоновых тел. Эти треугольники включают в себя и стороны золотого прямоугольника с соотношением сторон 1:Ф.

Причем это не искусственно подобранные параметры-величины, а обусловленные следствия введения-применения комплексной ЗП по всем правилам логического определения-построения евклидового деления в крайнем и среднем отношении.

Для сравнения: по формуле Эйлера сумма экспонент e^i π/k + e^–i π/k = 2·cos(π/k) принимает при k = 2 ÷ 6 значения 0, 1, √2, Ф, √3.

В то время как золотое сечение на вещественной оси – вырожденный (сложившийся) золотой треугольник, в котором третья сторона равна сумме двух других сторон.

Численные значения параметров золотых треугольников:

остроугольный:

– стороны (a, b, c) = (ф, ф√2, 1) ≈ (0.618, 0.874, 1);

– площадь S = ф√3/4 ≈ 0.268, периметр P = Ф + ф√2 ≈ 2,492...;

– высоты (h_a, h_b, h_c) = √3/2 · (1, 1/√2, ф) ≈ (0.866, 0.612, 0.535);

– медианы (m_a, m_b, m_c) = (√(5–3ф)/2, 1/√2 = cos45⁰, √(5–6ф)/2) ≈ (0.887, 0.707, 0.568);

– углы (α, β, γ) = (√(3/8), 1/2, ф²/√8) ≈ (37.76, 60, 82.24)⁰;

– радиус описанной окружности R = abc/(4S) = ф√(2/3) ≈ 0.505;

– радиус вписанной окружности r = S/p = √3/(2Ф² + √8) ≈ 0.215.

тупоугольный:

– стороны (a, b, c) = (ф, 1, √2) ≈ (0,618, 1, 1.414);

– площадь S = ф√3/4 ≈ 0.268, периметр P = Ф + √2 ≈ 3.032;

– высоты (h_a, h_b, h_c) = √3/2 · (1, ф, ф/√2) ≈ (0.866, 0.535, 0.378);

– медианы (m_a, m_b, m_c) = (√(5+ф)/2, √(5–2ф)/2, ф/√2) ≈ (1.185, 0.970, 0.437);

– углы (α, β, γ) = (22.24, 37.76, 120)⁰;

– радиус описанной окружности R = abc/(4S) = √(2/3) ≈ 0.817;

– радиус вписанной окружности r = S/p = ф√3/(2Ф + √8) ≈ 0.177.

Говоря о взаимосвязи длин сторон правильных многоугольников, особенно пятого и шестого порядков, следует также упомянуть известное соотношение b₅² = b₁₀² +1 между длинами сторон правильных 5-угольника и 10-угольника, вписанных в единичную окружность R = 1, которое можно найти в книгах по геометрии, например [6, с. 149].

С учетом длины шестиугольника b₆ = 1 мы приходим к целочисленной модификации пифагоровой тройки (по количеству вершин): прямоугольный треугольник, образованный сторонами b_k правильных фигур (5-угольника, 10-угольника и 6-угольника), вписанных в единичные окружности [7] (см. рисунок).

Таким образом, дуально-комплексная золотая пропорция проходит красной линией через все пять платоновых тел, собирая их бусинками на одной золотой ниточке в самом лучшем виде. Или словами великого комбинатора: «На блюдечке с золотой каемочкой».

Числовые свойства величин с квадратным корнем из трех.

В комплексном золотом сечении ключевым иррациональным параметром является квадратный корень √3. Он равен диагонали правильного куба с единичным ребром, который символизирует триортогональные оси и выражает наиболее характерный признак объемных тел в трехмерном евклидовом пространстве.

Корень из трех √3 численно определяет такие параметры (для правильных геометрических фигур и тел, если иное не оговорено):

• тангенс угла tg 30^o;
• пространственная диагональ куба со стороной =1; диаметр описанной сферы;
• гипотенуза прямоугольного треугольника со сторонами 1 и √2;
• высота треугольника со стороной =2;
• сторона треугольника, у которого радиус описанной окружности =1;
• диагональ прямоугольника на стороне квадрата 1×1 и его диагонали;
• расстояние между параллельными сторонами 6-угольника со сторонами =1;
• отношение диаметра сферы к длине ребра вписанного куба;
• площадь поверхности тетраэдра с единичным ребром;
• половина площади поверхности октаэдра с единичным ребром;
• пятая часть площади поверхности икосаэдра с единичным ребром;
• из степени квадратной матрицы (1, 2; 1, 3)ⁿ =(a₁₁, a₁₂; a₂₁, a₂₂) следует √3 = 2· lim_n→∞ a₂₂/a₁₂ –1;

половина квадратного корня из трех √3 / 2:

• отношение высоты треугольника к его стороне;
• радиус вписанной окружности в шестиугольник со стороной =1;
• косинус угла cos 30⁰;
• действительная часть i ^1/3 или кубического корня из i ;
• десятая часть площади поверхности икосаэдра с ребром =1;
• радиус описанной сферы куба с единичными ребрами;
• высота (от вершины до противоположной грани) тетраэдра с ребром =1;
• площадь треугольника (30-60-90)⁰ c минимальным катетом = 1;
• высота треугольной грани тетраэдра, октаэдра и икосаэдра с ребром =1; при этом пространственные диагонали икосаэдра равны Ф и √(2+Ф);
• радиус описанной сферы додекаэдра равен Ф·(√3 / 2);
• радиус вписанной сферы икосаэдра равен Ф²/(2√3);

величина (1+√3) / 2 численно означает:

• положительный корень квадратного уравнения x² – x – 1/2 = 0
• max {a, b}, где {a, b} – единственное решение a + b = 1 и a² + b² = 2 (подразумевая также ab = –1/2 и a³ + b³ = 5/2 без решения для a, b);
• величина 1+√3:
• периметр треугольника (30-60-90)⁰ с наибольшим катетом = 1;
• длина второй по длине диагонали 12-угольника со стороной =1;
• бесконечная цепная дробь 2 + 2/(2 + 2/(2 + 2/(2 + ...))).

Куб с его пространственной диагональю √3 – единственный правильный многогранник, которым можно заполнить пространство. Пространственный паркет можно также составить из неправильных тел: произвольного параллелепипеда, правильной треугольной призмы, правильной шестиугольной призмы, ромбододекаэдра, параллелоэдров, сочетания кубооктаэдров и октаэдров (обычных и усеченных) [8] и др.

Куб разбивается на 4 правильные четырехугольные пирамиды, каждая из которых – на две равные треугольные пирамиды, – они также заполняют пространство.

Мир комплексных чисел и комплексного золотого сечения.

Комплексные числа – сверкающая вершина всей системы чисел (С.Строгац).

Они помогают из-за обратной стороны зеркала справиться с недостатками вещественных чисел (Х.Вагенсберг). Их можно складывать и вычитать, умножать и делить.

Они лишены главного недостатка действительных чисел. Из них всегда можно извлечь корень любой степени, получив в результате снова комплексное число.

Комплексный мир удивительный. Он невероятным образом объединяет совершенно разные константы. Английский математик Б.Пирс как-то написал на доске равенство i ^–i = √(e^π) и сказал: «Нет ни малейшего представления, что бы это значило. Но мы можем быть уверены, это значит что-то чрезвычайно важное» [9].

Волшебный мир фракталов начался с группировки-объединения возводимых в квадрат комплексных чисел. Впервые описал 25-летний француз Г.Жюлиа (1918) на примере поведения точки последовательности z_n+1 = z_n² + c на комплексной плоскости в зависимости от комплексного числа-параметра c, порождая целые миры сложных самоподобных структур.

Основная теорема алгебры утверждает, что всякий отличный от константы многочлен одной переменной с комплексными коэффициентами имеет, по крайней мере, один корень в поле комплексных чисел. Утверждение справедливо и для многочленов с вещественными коэффициентами.

К мнимой числовой оси многие относятся с недоверием, предубеждением. Напрасно. Видимо, и в глобальном потеплении они больше всех винят холодильники.

Довольно странная позиция. Ведь чисел в природе нет. Вообще никаких чисел, начиная с натурального ряда. Всё это искусственные образования, как результат деятельности мозговых извилин человека. Школьная таблица умножения не пугает, хотя чистая абстракция, которая помогает в повседневной жизни и не более того. От компьютера никто не бежит, как черт от ладана, хотя его внутренность жонглирует только ноликами и единичками. Отчего же такая предвзятость к комплексному числу? – Если оно – святой Грааль и апогей-венец единого числового братства во главе c математическим богом-троицей в трех ипостасях: нуля и двух единиц: 0, 1, i ² = –1.

Именно поэтому комплексное золотое сечение – что ни на есть настоящий математический объект, стоящий над воспринимаемой реальностью. Вместе с обычным золотым сечением они вместе призваны "замкнуть" на себя многие важные процессы и явления, происходящие в окружающем нас мире, с выходом на просторы Вселенной.

«Если в глобальном проявлении окружающий мир упорядочен пропорциональными структурами, то велика вероятность, что в его основе лежит именно модель золотого сечения. Тогда пропорция с основанием константы золотого сечения становится неким универсальным кодом Вселенной. При этом деление живых клеток пополам синтезирует организмы, а золотая пропорция выступает в роли структурирующей подосновы» [10].

Действительная и комплексная золотые пропорции "замыкают" платоновы тела в единую систему: тетраэдр (треугольная пирамида) – 4▲, октаэдр – 8▲, икосаэдр – 20▲, гексаэдр (куб) – 6■ , додекаэдр – 12 . Это выпуклые многогранники с одинаковыми гранями в виде правильных многоугольников, имеющие пространственную симметрию и форму, пригодную для игральных костей. Теэтет Афинский доказал, что таких тел ровно пять. Причем, количество ребер тетраэдра, куба и икосаэдра равно (n+1)·(n+2) и соответственно составляет 2·3 = 6, 3·4 = 12, 5·6 = 30, где n – размерность: 1 – многообразия вещественных чисел, 2 – комплексных чисел и 4 – кватернионов [11, с. 21].

В нашей работе [12] показано, что наибольшая плотность конусной упаковки пространства соответствует двенадцати направлениям граней додекаэдра и выражается через число золотого сечения ρ = 6(1 – sin arctg Ф) ≈ 89,6 %.

Комплексное золотое сечение – такое же, как и действительное, только построенное через механизм противоположных чисел, выражаемый математическим отрицанием.

Пропорция функционирует через взаимодействие и сравнение противоположностей.

Сопоставление осуществляется использованием знака минус, который идентифицирует противоположности относительно нулевой точки отсчета. Подобно проявлению в моделях: белое – черное, левое – правое, ин-янь и т.п.

Подведение промежуточных итогов.

«Главной целью всех исследований внешнего мира должно быть открытие рационального порядка и гармонии, которые бог ниспослал миру и открыл нам на языке математики» (И.Кеплер). «Природа стремится к максимуму разнообразия через минимум форм» (Д.Менделеев).

В целом проецирование золотой пропорции на комплексную плоскость находится в общем русле развития логических устремлений человеческого разума. Хотя требуются определенные мозговые усилия для объективизации самого понятия, подтверждения его истинности, расширения сферы применимости и т.п. На наш взгляд, появление единого (общего) золотого сечения проливает свет на корни-истоки его присутствия в целостном множестве форм живой и неживой природы.

Вещественная и комплексная ЗП переплетаются, взаимодополняют, конвергируют.

В макроскопической кристаллографии различают три основных вида симметрии: поворотно-осевая, зеркально-плоскостная (отражение) и центрально-точечная. В классических кристаллах существуют только оси симметрии 1–4 и 6 порядка. На осевую симметрию 5 порядка наложено табу. Наоборот, в живых объектах она широко распространена. Причем наиболее ярко проявляется в переходной области между живым и неживым. Переходя к мельчайшим размерам, мы всё ближе переходим от неживой природы – к живой материи.

Происходит процесс конвергенции или сближения-схождения.

Единая дуально-комплексная золотая пропорция – связно-объединенная модель конвергенции пятого и шестого порядка осевой симметрии. Своеобразная матрица устройства и развития мира, основа гармонии природных объектов и явлений.

В прошлом веке были открыты квазикристаллы – необычные материалы с осевой симметрией пятого порядка. По симметрии не кристалл, но имеет дальний порядок трансляционной симметрии, свойственный обычным кристаллам. Куда бы ни сдвинулись от исходной ячейки, везде одинаковая "строительная картина". Такой себе «живой неживой объект».

Приведенное выше построение дуально-комплексного золотого сечения является теоретической основой существования квазикристаллов. Через константу золотого сечения Ф = (1 + √5)/2 и соответствующий центральный угол пентагона 72⁰ = 360/5 осуществляется осевая симметрия пятого порядка, через квадратные корни √2 и √3 – дальний порядок кристалла с паркетным замощением плоскости посредством квадратов и треугольников и/или шестиугольников.

Сам квазикристалл выступает в роли переходной формы между живым и неживым:

1) ещё неживое, но уже не мертвое, – с ростом-развитием согласно двучленно-аддитивной рекурсии золотого сечения;

2) уже неживое, но ещё не мертвое, – сгусток биологической энергии ("душа") теплица, биологический объект остывает, костенеет – ("живой труп").

Единая дуально-комплексная золотая пропорция и разносторонние золотые треугольники объединяют «под одной крышей» три квадратных корня √2, √3, √5 – ключевые иррациональные числа геометрических фигур с осевой симметрии 3–6 порядков. Среди них и легендарный корень √2 – диагональ единичного квадрата, положившие начало теории несоизмеримости и иррациональных чисел.

Вообще диагональ – один из важнейших параметров геометрии. В чем-то "помогают", иногда наоборот "мешают". На плоскости существует два правильных многоугольника, у которых все диагонали равны между собой: квадрат и пятиугольник. В правильном октаэдре все диагонали равны между собой. В кубе все пространственные диагонали равны между собой.

Диагонали пятиугольника равны, но им нельзя замостить плоскость.

Один из крупнейших геометров ХХ века канадец Г.Кокстер доказал, что правильный 2m-угольник с четным количеством сторон (зоногон) может быть разбит на m(m –1)/2 ромбов с разными диагоналями.

В частности, разбивка десятиугольника дает ромбы (см. рисунок), которыми можно замостить паркет на всей плоскости: мозаика Пенроуза, как непериодическое разбиение плоскости.

Вместо заключения.

Нам ещё предстоит более углубленное осмысление единой (общей) дуально-комплексной золотой пропорции (ЗП), объединяющей действительную и комплексную ЗП.

Как необходимый обусловленный этап на тернистом пути приближения к недостижимому полному знанию.

Но уже сейчас видно, что единая золотая пропорция отражает целостный диалектический закон единства и взаимодействия противоположностей, с одинарным и двойным отрицанием и переходом количества в качество.

На наш взгляд, дуально-комплексная золотая пропорция играет доминирующую роль в мироздании. Не как культовый символ, современная байка или раздутый миф гармонии в контексте надуманной эстетики или вымышленной красивости. Но гармонии в виде когерентно-связной согласованности разнородных и даже противоположных элементов.

Как гномон, кирпичик, "математический атом или электрон".

Если мировую гармонию можно как-то выразить в числовых пропорциях, то единая золотая пропорция занимает одну из доминирующих позиций.

По Гераклиту гармония – единство, согласованность, уравновешенность, взаимодействие противоположностей – частей целого. Всё возникает через противопоставление. Он различал явную и скрытую (не проявленную) гармонию. Причем скрытая сильнее явной. – Именно такой нам видится комплексная золотая пропорция.

Действительной ЗП в костных системах нет. Могут проявляться отдельные "проблески" и только. Нет ни одного достоверного факта, свидетельствующего о присутствии констант ф, Ф в неживых объектах, системах и процессах. В то же время дуально-комплексная ЗП на каждом шагу, можно и на улицу не выходить.

Наиболее вероятно, в неживой природе находят число 1 – (√3 –1)/2 ≈ 0,634, которое ошибочно принимают за малую константу действительного золотого сечения ф ≈ 0,618.

В завершении сформулируем три задачи дальнейших исследований:

1) На современном языке, существует единственная гладкая связная правильная кривая в трехмерном пространстве – это спираль. Прямая и окружность – её частные случаи. Правильная кривая в том смысле, что каждая её точка равно окружена остальными точками кривой. Согласно дифференциальной геометрии, кривизна и кручение в каждой точке спирали постоянны.

Задача: построить спирали на основе золотых треугольников общего вида, не только равнобедренного или прямоугольного.

2) Предварительные расчеты показали, что функция v ^x + (–v)^–x, как непрерывный аналог чисел Люка двучленно-аддитивной рекурсии, образует замкнутую алгебраическую кривую наподобие улитки Паскаля только при v = (1 ± i√3)/2.

В остальных случаях формируются спиралевидные формы.

Задача: найти общие функциональные закономерности фазовых портретов комплексной золотой пропорции.

3) Советский академик А.Александров в свое время рассмотрел [13] заполнение многогранниками n-мерного, односвязного, полного пространства R_n постоянной кривизны, то есть евклидова пространства либо пространства Лобачевского.

Чтобы правильным многогранником можно было однозначно заполнить пространство R_n, прикладывая его по целым граням, необходимо и достаточно, чтобы его двугранные углы, то есть углы между (n−1)-мерными гранями, смежными по (n−2)-мерным граням, составляли целую часть 2π.

Задача: заполнить пространство R_n многогранниками, построенными на основе комплексной золотой пропорции.

Benedicite…

Литература:

1. Василенко С.Л. Квазизолотая пропорция в структурированных системах // АТ. – М.: Эл. № 77-6567, публ. 16054, 30.08.2010. – URL: trinitas.ru/rus/doc/0016/001c/00161694.htm.
2. Бохенский Ю.М. Современная европейская философия. Пер. с нем. – М.: Научный мир, 2000. – 256 с.
3. Яглом И.М. Комплексные числа и их применение в геометрии. – М.: Физматгиз, 1963. – 192 с.
4. Василенко С.Л. Новый взгляд на систематику «Фибоначчи – золотое сечение» // АТ. – М.: Эл. № 77-6567, публ. 16189, 01.12.2010. – URL: trinitas.ru/rus/doc/0016/001c/00161734.htm.
5. Василенко С.Л. Семейство золотых треугольников и параллелограммов // АТ. – М.: Эл. № 77-6567, публ. 26931, 23.01.2021. – URL: trinitas.ru/rus/doc/0016/001h/00164608.htm.
6. Адлер А. Теория геометрических построений: пер. с нем., 3-е изд. – Л.: Учпедгиз, 1940. – 232 с. – URL: http://ilib.mirror1.mccme.ru/djvu/geometry/adler.htm.
7. Василенко С.Л. Метаморфозы представлений: от деления в крайнем и среднем отношении – до золотой пропорции // АТ. – М.: Эл. № 77-6567, публ. 22463, 01.09.2016. – URL: trinitas.ru/rus/doc/0016/001e/00163040.htm.
8. Заполнение пространства многогранниками / Математика, 2009, № 5. – URL: mat.1sept.ru/view_article.php?ID=200900503.
9. O'Connor J.J., Robertson E.F. The number e / MacTutor History of Mathematics Archive. – Sept., 2001. – URL: mathshistory.st-andrews.ac.uk/HistTopics/e/.
10. Василенко С.Л. Дуализм модели золотой пропорции // АТ. – М.: Эл. № 77-6567, публ. 23987, 23.11.2017. – URL: trinitas.ru/rus/doc/0016/001f/00163516.htm.
11. Арнольд В.И. Геометрия комплексных чисел, кватернионов и спинов. – М.: МЦМНО, 2002. – 40 с.
12. Василенко С.Л. Золотые купола в задаче конусной упаковки евклидового пространства // Научно-техническая б-ка SciTecLibrary. – 17.07.2011. – URL: sciteclibrary.ru/rus/catalog/pages/11225.html // АТ. – М.: Эл. № 77-6567, публ. 17147, 26.12.2011. – URL: trinitas.ru/rus/doc/0232/013a/02322102.htm.
13. Александров А.Д. О заполнении пространства многогранниками // Вестник ЛГУ, сер. матем., физ., хим., 1954. № 2. – С. 33-43.

[Обсуждение на форуме «Публицистика»]