Дискуссии - Наука

С.Л. Василенко

Введение. Треугольник – первая геометрическая фигура, встречающаяся в древних орнаментах. Его изображения с соответствующими задачами на построение находят в папирусах и старинных индийских книгах.

Треугольник – одна из первых плоских фигур. Отсюда и символ поверхности вообще.

В математике выделен специальный раздел тригонометрии (греч. trigonon треугольник + metro метрия), который своим рождением обязан исследованию зависимостей между сторонами и углами треугольника, а сегодня изучает алгебраические соотношения тригонометрических функций и их приложения в геометрии [1].

Отношения сторон, углов, высот и прочих элементов треугольника образуют около 3600 характерных точек [2] со своей геометрией, симметрией и пропорциями.

Начиная с Нового завета, традиционный христианский Бог троичный в лицах. «Если бы треугольники создали себе бога, он бы был с тремя сторонами» (Ш.Монтескье, 1689–1755).

Золотой параллелограмм. Рассмотрим евклидову плоскость.

В литературе известен золотой прямоугольник 1×Ф. Его отличительная особенность: после удаления квадрата 1×1 оставшаяся часть 1×ф снова являет золотой прямоугольник, с теми же соотношениями геометрических размеров, Ф = (1 + √5) / 2, ф = Ф^–1 – константы золотого сечения (ЗС).

Прямоугольник – частный случай параллелограмма с прямыми углами.

Вполне логично распространить его свойства на параллелограмм общего вида с произвольными внутренними углами.

Определение. Золотой параллелограмм – параллелограмм, у которого две стороны соотносятся как 1:Ф.

После умножения на ф = Ф^–1 соотношение становится равным ф:1. То есть в золотых фигурах отношение сторон составляет 1:Ф или 1:ф. Порядок не имеет значения.

По аналогии с золотым аналогом, если от золотого параллелограмма 1×Ф отрезать ромб 1×1, то снова получим золотой параллелограмм, с теми же соотношениями геометрических размеров сторон и диагоналей. Углы не изменяются.

Золотой параллелограмм – это не блажь, а необходимость упорядочения и развития теории. В частности, он образуется при векторном отображении двучленно-аддитивной рекурсии v_n+1 = v_n + v_n–1 на комплексной плоскости [3], независимо от взаимного расположения двух начальных векторов, длины которых соотносятся как v₀ : v₁ = 1 : Ф.

Построение золотого параллелограмма простое: сначала вычерчиваем золотой прямоугольник и далее обычным вращением боковых сторон переводим их на направляющие стороны параллелограмма (см. рисунок).

Переход к параллелограмму, по сути, сводится к рассмотрению геометрических фигур в декартовой косоугольной системе координат.

Золотые треугольники. Диагонали параллелограмма делят его на два равных треугольника. Каждый из таких треугольников золотого параллелограмма вполне логично назвать золотым треугольником.

Определение. Золотой треугольник – треугольник, у которого две стороны соотносятся как 1:Ф.

Золотой параллелограмм составлен из двух равных золотых треугольников.

Обозначим γ – угол между сторонами 1:ф. Третья сторона вычисляется с помощью теоремы косинусов c = √(1 + ф² – 2ф·cosγ), описанной ещё в предложениях 12-13 "Начал" Евклида [4, с. 76-78].

Золотых треугольников (ЗТ) много. Для их идентификации можно добавлять уточняющие прилагательные: равнобедренные ЗТ (их всего два), прямоугольные ЗТ (их всего два, один из которых треугольник Кеплера) и т.д. (см. рисунок).

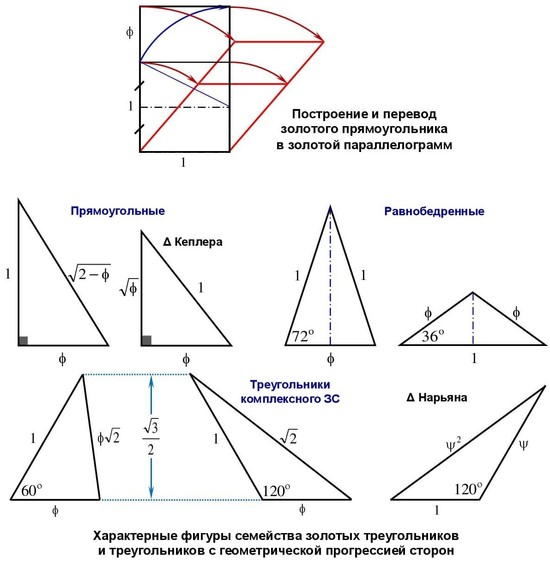
Имеем два прямоугольных треугольника. Один из них – треугольник Кеплера, длины сторон которого относятся как ф:√ф:1 и образуют геометрическую прогрессию.

Имеем два равнобедренных треугольника с острым и тупым углами при вершине.

Построение одного из них описано Евклидом в предложении 10 четвертой книги: построить равнобедренный треугольник, имеющий каждый из углов при основании, вдвое большим остающегося [4, с. 132–133].

Золотые равнобедренные треугольники имеют соотношения углов 1:1:3 и 2:2:1. Суммы частей равны 5. Именно поэтому они присутствуют в звездчатом пятиугольнике (пентаграмме): каждый острый угол 36^о воспроизводит золотой треугольник 1:1:ф, а тупой угол 108^о – золотой треугольник ф:ф:1.

Треугольники с геометрической прогрессией сторон.

Пусть длины сторон треугольника образуют геометрическую прогрессию 1, q, q² c её знаменателем q.

Косинус угла между сторонами 1 и q равен cos γ = (q⁴ – q² – 1) / 2q.

1) Если q = Ф, то cos γ = 1 и угол γ = 0. Если q = ф, то cos γ = –1 и угол γ = π.

То есть для данных значений q треугольник вырождается, превращаясь в отрезок c точкой золотого сечения и длиной 1 = ф + ф² или Ф² = Ф + 1.

Допустимо обратное прочтение: золотое сечение отрезка – это вырожденный треугольник с геометрической прогрессией сторон.

Таким образом, константа золотого сечения Ф является предельным значением для построения треугольника с геометрической прогрессией (1, q, q²) сторон: ф < q < Ф.

2) Если q = √Ф, то cos γ = 0 и угол γ = π/2 – золотой прямоугольный Δ-Кеплера.

Треугольник Кеплера – прямоугольный треугольник, в котором длины двух катетов и гипотенузы образуют геометрическую прогрессию [5, с. 81–85]: гипотенуза / больший катет = больший катет / меньший катет.

На эту тему один известный исследователь носится как с писаной торбой и выстраивает несуществующие мифы относительно некоего мета-треугольника со сторонами (√Ф, Ф, Ф√Ф), который де-факто является обычным треугольником Кеплера [1] с единичной высотой как числовой мерой. Со всеми вытекающими свойствами.

3) Ещё один примечательный случай: cos γ = 0,5 и угол γ = π/3 = 60^о.

Знаменатель прогрессии q находится из уравнения q⁴ – q² – q – 1 = 0 или после деления на (q + 1) – кубического уравнения q³ – q² – 1 = 0.

Действительный корень равен q = ѱ = (c/2 + 2/c + 1)/3 ≈ 1,465571.., c = ³√(116 + 12√93).

Это четвертое наименьшее число Пизо или Писота.

Соответствующую рекурсию f_n = f_n–1 + f_n–3 для тринома q³ – q² – 1 с единичными начальными условиями иногда называют «коровьей последовательностью» [6, с. 47], которую предложил индийский математик Нараян в 14 веке [7].

Некоторые любители экстравагантной терминологии не преминули назвать его «суперзолотым сечением», застолбив место в Википедии. Соответственно употребляются термины: «сверхзолотое число» и «сверхзолотой прямоугольник» [6, с. 51]. На наш взгляд, ничего супер-пупер-золотого здесь нет. Оценка больше носит эмоциональный характер и подчеркивает, что числа Фибоначчи с их золотым аттрактором не единственны и допускают расширение в похожем подмножестве, в частности, триномов старших степеней [7].

4) На рисунке также представлены треугольники комплексного золотого сечения, в которых сторона единичного квадрата и его диагональ "замыкаются" через константу ЗС.

В составленном параллелограме углы сооносятся как 1:2.

Это особые треугольники, объединяющие в себе действительное и мнимое золотое сечение, как предмет дальнейших углубленных исследований.

Всё сбудется, стоит только расхотеть (Ф.Раневская)...

Литература:

1. Василенко С.Л. Треугольник Кеплера как объединитель теоремы Пифагора, золотого сечения и современных мифов // АТ. – М.: Эл. № 77-6567, публ.22385, 05.08.2016. – URL: trinitas.ru/rus/doc/0016/001e/00163016.htm.
2. Kimberling C. Triangle Centers and Central Triangles // Congr. Numer, 1998, 129, 1-295.
3. Василенко С.Л. Золотое сечение в векторном представлении линейной двучленно-аддитивной рекурсии // АТ. – М.: Эл. № 77-6567, публ. 26763, 03.11.2020. – URL: trinitas.ru/rus/doc/0016/001h/00164538.htm.
4. Начала Евклида. Книги I–VI: пер. с греч. и комментарии Д.Д. Мордухай-Болтовского. – М. –Л.: ГИТТЛ, 1948. – 448 с.
5. Roger Herz-Fischler. The shape of the Great Pyramid. – Wilfrid Laurier University Press, 2000. – 294 p.
6. Крилли Т. Математика. 50 идей, о которых нужно знать. – Пер. с англ. – М.: Фантом Пресс, 2014. – 208 с.
7. Василенко С.Л. Триномы старших степеней: от деления пополам и золотого сечения – до модели единичного абсолюта // Научно-техническая б-ка SciTecLibrary. – 07.06.2015. – URL: sciteclibrary.ru/rus/catalog/pages/15014.html // АТ. – М.: Эл. № 77-6567, публ. 21966, 09.04.2016. – URL: trinitas.ru/rus/doc/0016/001e/00162924.htm.

[Обсуждение на форуме «Публицистика»]