|
|
|
В.Ю. Татур
Содержание
Введение
Физическая точка
Ментальные пространства
Р-адические числа и фрактальность человека
Итак будьте совершенны,
как совершенен Отец ваш Небесный
(Мф. 5:48)
Введение
Удивительно устроено познание человека. Даже когда набирается множество фактов, противоречащих или изменяющих выбранную человеком картину мира, он продолжает упорно следовать отжившей модели, не замечая того, что его усилия напрасны. Вместо того, чтобы повернуть, вернуться назад, осмыслить новые данные, изменить вектор движения, он начинает биться в гносеологическую стену в надежде ее проломить. А для оправдания этого безсмысленного действа он придумывает разные причины, модели, которые превращают эту гносеологическую стену либо в непреодолимое препятствие, либо в ничто, тем самым порождая надежду на осмысленность усилий. Человек либо успокаивается, и познание умирает, либо он превращается в пророка, свет истины которого не понимают окружающие.
Наглядный пример тому понимание и применение модели точки. А, по сути, это вопрос о правомерности используемых геометрических моделей, правил их преобразований, о границах применимости моделей действительности.
Если не понимать границ применимости моделей, то мы получаем такие абстракции, которые не только не ведут к истине, но уводят от нее.
Эквилибристика ума при решении тех или иных задач математики должна восприниматься только как эквилибристика ума, если в условиях задачи не оговорены граничные условия применения метода.
Например, представление о точке, как нульмерном объекте, сопряжено с противоречием непрерывности линии, которая состоит из множества точек. Это противоречие, например, приводит к тому, что отрезки разной длины по количеству точек равны между собой.
Поясню на примере.
Для этого нарисуем угол и две параллельные секущие. А, В, С, D – точки пересечения секущих со сторонами угла.
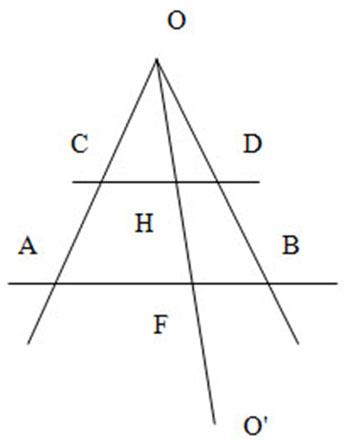
Через точки F и H на этих секущих проведем линию ОО’.
Тогда имеем следующую проблему.
Для любой точки на отрезке AF и на отрезке CH всегда найдется такая точка, что через них и точку О можно будет провести прямую. Иначе говоря, как бы, количество точек на AF и CH одинаково. Множества их равномощны, т.е. между точками этих двух отрезков можно установить взаимно однозначное соответствие. Но это будет справедливо для любого отрезка на любой секущей проведенной как угодно близко к точке О. С точки зрения счетных множеств длина AF равна CH. Этот наглядный парадокс, конечно, проистекает из противоречия в аксиоматике, когда из нульмерных непротяженных объектов, каким является математическая точка, строят не нульмерный протяженный объект или просто утверждают, что это – два разных математических объекта, как в геометрии Эвклида точка и прямая. Но о нем забывают, когда применяют геометрические построения и преобразования к реальному пространству и движению. Все дело в том, что мощность непрерывного множества больше, чем дискретного. Иначе говоря, сколько математических точек не ставь, никогда не получишь непрерывную линию. Это противоречие свойственно для всех хаусдорфовых пространств, к которым относятся все метрические и метризуемые пространства, в том числе евклидовое.
Противоречия математической модели реальности наиболее ярко были сформулированы в апориях Зенона, например, касающихся бесконечной делимости пространства. Мы до сих пор пользуемся математическими моделями движения, основанными на геометрии, созданной еще в V веке до н. э. Эта геометрия опиралась на такие понятия, как тело, поверхность, фигура, линия — и на понятие точки пространства, не имеющей никаких собственных измеримых характеристик. То есть мы до сих пор пользуемся моделью классической кривой, которая считается одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие решается либо через монадологию Лейбница, получившую второе рождение в нестандартном анализе, разработанном Абрахам Робинсон в XX веке, либо через подход, предложенный Коши в XIX веке с использованием понятия предела. Но к реальному движению второй подход не имеет отношения. Это – чисто математический приём. Он не разрешает апории Зенона, который как раз ставит под сомнение не логику математической модели, а применимость ее к реальному движению.
То, что проблема математической модели реальности не решена, понимали все ведущие математики и физики
XX века.Так Гильберт и Бернайс высказывали мнение о неадекватности непрерывной, бесконечно делимой математической модели физически дискретной материи. Они отмечали: «мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени».[1]
Николя Бурбаки писал: «Вопрос о бесконечной делимости пространства (бесспорно, поставленный ещё ранними пифагорейцами) привёл, как известно, к значительным затруднениям в философии: от Элеатов до Больцано и Кантора математики и философы не в силах были разрешить парадокса — как конечная величина может состоять из бесконечного числа точек, не имеющих размера.» [2]
А Ричард Фейнман даже заявил: «Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что [в квантовой механике] она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны.» [3]
Наличие этих противоречий означает, что не верна и аксиома Архимеда, которая гласит, что если есть прямая и на ней обозначены два отрезка а и b с началом в одной точке, причем а <b, то, прикладывая меньший отрезок а вдоль прямой ограниченное число раз, мы, в конце концов, превзойдем больший отрезок b. То есть для данного отрезка B длины b и другого (меньшего) отрезка A длины a, a < b, можно указать такое натуральное число n, что n • a > b.
Это также означает, что дифференциальное исчисление, в котором приращение аргумента стремится к нулю (ньютоновская версия), содержит в себе неразрешимое противоречие. Мы это противоречие просто не хотим видеть, поскольку при определенных размерах исследуемых областей вычисления дают результаты близкие к экспериментальным. Мы перескакиваем через проблему путем различных математических манипуляций, как, например, процесс перенормировки в квантовой электродинамике. В результате укореняется модель, которая дает результаты, но у которой нет объяснений. Это как птолемеевская модель солнечной системы: вычисления дают правильные результат, но к реальной солнечной системе эта модель не имеет отношения.
Сейчас модель точки переживает кризис, когда очевидно, что предыдущая модель работает, но реальность иная и требует кардинально иной модели. Впереди всеобщая «коперниканская» революция модели пространства.
Но кому это интересно, если можно продолжать заниматься эквилибристикой ума, рассуждать об иррациональных числах, которые не имеют никакого отношения к физическому миру. Разве человек (физик, математик и т.д.) может согласиться, что все его труды напрасны? Что все его модели, диссертации, звания и должности основаны на ложном фундаменте? Конечно, нет. Он будет продолжать следовать привычной модели, убеждая себя и других, что в его результатах есть польза, что можно и нужно именно так представлять модель точки, как он привык. А поскольку точка – фундаментальное понятие, то у развития науки появляется огромные тормоз в виде сотен тысяч ученых, наученных и приверженных определенной картине мира, которые будут всячески противиться новому взгляду. Им так проще, им так комфортнее, более хлебно.
Но что же идет на смену математической точки? Физическая. А вместе с ней иная модель пространства, объектов в нем, связей между ними и, конечно, иное представление о человеке и его мышлении.
Физическая точка
Наш образ мира сформирован на итерациях от эмпирического факта к модели, от неё к эксперименту и обратно к модели. Именно эксперимент, практика дает нам основания для оценки существующей модели, но в силу ограниченности возможностей человека результаты любого эксперимента предстают в виде конечных чисел, которые относятся к множеству рациональных чисел, т.е. таких, которые можно представить в виде дроби m/n, где числитель m — целое число, а знаменатель n — натуральное число (1,2,3 …). В научных экспериментах мы никогда не имеем дела, например, с бесконечными десятичными дробями, т.е. с иррациональными вещественными числами. При этом трудно себе представить, что когда-то будет такая точность измерений, которая позволит получить бесконечное количество знаком после запятой, т.е. интерпретировать результат, как вещественное число.
Реальным физическим ограничением применимости аксиомы Архимеда являются основания квантовой механики, согласно которой невозможно измерить расстояния меньше планковского, которое задается формулой lpl = √(ħG/c3) ≈1,616 229(38)·10−35 м, где ħ ( h/2π) - постоянная Планка, с – скорость света и G - гравитационная постоянная.
Иначе говоря, согласно принятым геометрическим представлениям, мы должны иметь возможность измерить сколь угодно малые расстояния, но в виду физического ограничения в виде планковской длины в реальном физическом пространстве такое измерение невозможно. Таким образом, мы приходим к выводу, что геометрия риманова пространства неадекватно описывает свойства реального физического пространства на очень малых расстояниях.
Впервые на то, что лишь рациональные числа являются физическими числами, обратили внимание И.В. Волович и В.С. Владимиров.
Но если для описания физического мира отправной точкой следует брать поле рациональных чисел Q, т.е. алгебру, для элементов которой определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), которому соответствует неполное метрическое пространство, то как перейти к математическим моделям таких полей чисел, которым соответствует полное метрическое пространство, т.е. такое, в котором каждая фундаментальная последовательность сходится?
Известно, что геометрическому понятию расстояния между двумя рациональными числами соответствует аналитическое понятие нормы на Q.
Какие же нормы есть на поле рациональных чисел Q?
Удивительно, но согласно теореме Островского их всего две: ||x|| и ||x||р , р =2,3,…, где ||x|| - вещественная норма рационального числа x, а ||x||р - р –адическая норма, которая измеряет, на какую степень p делится рациональное число.
Этими нормами исчерпывают все нетривиальные неэквивалентные нормы поля рациональных чисел Q. Иначе говоря, любая норма на поле рациональных чисел Q эквивалентна либо вещественной норме (обычному абсолютному значению), либо одной из p–адических норм, где р - простое число.
Вещественной нормой рационального числа x называется его модуль |x|, т.е. ||x||=|x|. Полем вещественных (действительных) чисел называется пополнение поля рациональных чисел по вещественной норме, которая удовлетворяет условиям
(1) ||х||≥0, причем ||х||=0 при х=0
(2) ||х•y|| = ||х||•||y||
(3) ||х+y||≤||х|| + ||y||
для любых рациональных чисел х, у.
Р – адической нормой рационального числа х, представленного единственным образом в виде несократимой дроби x =p γ(m/n), где p есть простое число, γ есть целое число, m целое, n натуральное, а p, m, n взаимно просты, называется число
||x||p=p− γ, если x≠0, и 0, если x=0.
Р-адическая норма удовлетворяет следующим условиям
(1) ||х||≥0, причем ||х||=0 при х=0
(2) ||х•y|| = ||х||•||y||
(3') ||х+y||≤ max(||х||p, ||y||p) - усиленное неравенство треугольника
Норма, которая удовлетворяет неравенству (3'), называется неархимедовой.
Пополнение поля рациональных чисел Q по обычной, вещественной норме приводит к полю вещественных чисел R, а пополнение по р-адической норме – к полю р-адических чисел Qp для любого простого р. При этом р-адическое нормирование рациональных чисел является дискретным, т.е. норма может принимать лишь дискретное множество значений, в то время как вещественная норма дает непрерывное множество действительных чисел.
Поля p –адических чисел Qp – единственный примеры неархимедовых числовых полей, получаемых пополнением поля рациональных чисел Q по p–адической норме. После задания метрики dp(x,y)= |x-y|p, x,y ∈ Qр, индуцированной р-адической нормой, Qр становится полным метрическим пространством. Поскольку p–адическая норма неархимедова, то соответствующая ей метрика dp удовлетворяет сильному неравенству треугольника
dp(x,y) ≤ max[dp(x,z)p, dp(z,y)], x,y,z ∈ Qр
Метрика такого типа называется ультраметрикой, а – Qр ультраметрическим пространством для любого р.
Таким образом, модельный мир смотрит на рациональные числа с помощью двух кардинально различных не изоморфных друг другу состояний: поля действительных чисел R и поля р-адических чисел Qр, с уровня непрерывности и уровня дискретности, с точки зрения упорядоченного множества и неупорядоченного, связного и вполне несвязного пространства, пространства с размерностью и имеющего нулевую топологическую размерность,
c числовой прямой и c однородного дерева с ветвлением на р частей в каждой вершине.[4]Важно, что, с одной стороны, метрическое пространство может быть представлено в виде древовидной решетки, а с другой, - подпространство, натянутое на точки, для которых расстояние между ними удовлетворяет усиленному неравенству треугольника, является эвклидовым.
Идея применения р-адических чисел для описания пространства на расстояниях меньше планковского принадлежит В.С. Владимирову и И.В. Воловичу [5- 7].
Эта идея о том, что граница физической точки (если можно говорить о границе) есть граница двух расширений: до множества действительных чисел и до множества р-адических чисел. Если во вне физической точки мы получаем архимедов анализ, то внутри её царствует неархимедов. И что самое важное, согласно теореме Островского, есть только эти два нетривиальных способа расширения множества рациональных чисел.
Таким образом, пространство физической точки – это ультраметрическое пространство, топологическая размерность которого равно нулю.
Но какое отношение все эти построения имеют к человеку?
Для того чтобы ответить на этот вопрос, нужно сначала понять, что из себя представляет ультраметрическое пространство, подобием чего являются его объекты.
Ментальные пространства
Чему же соответствуют ультраметрические пространства Qp?
Очень чётко об этом написал А.Ю. Хренников в работе «Моделирование процессов мышления в р-адических системах координат»:
«В наших моделях р-адическая метрика имеет ясную когнитивную интерпретацию. Если две идеи имеют обширную общую ассоциацию, то они близки в р-адической метрике. … наши р-адические модели описывают ассоциативное мышление» [8, с.21]
Таким образом, ультраметрические пространства Qp есть форма описания ментальных пространств.
В своей работе «Р-адические числа, ультраметрика и ментально-вещественный мир» [4], я приводил размышления А.Ю. Хренникова [8] к описанию ментального пространств на основе р-адического анализа.
Оно, во-первых, не непрерывно, поскольку мысли нельзя делить до бесконечности, или это означает, что пространство не является связным. «Любое p-адическое дерево можно разбить на две части, не имеющие общей границы или, что эквивалентно, на две непересекающиеся части, являющиеся одновременно и открытыми, и замкнутыми» .[8, с. 11]
Во-вторых, оно дискретно и обладает иерархической структурой, т.е. для двух ментальных объектов всегда существует некоторый ментальный объект, который стоит в иерархической системе выше указанных двух.
В-третьих, оно не является однородным, т.е. существует жесткая иерархия: корень, ствол, ветви, ответвления, листья.
В-четвертых, это пространство ультраметрическое, т.е. два ментальных состояния являются близкими, если у них достаточно длинная общая часть дерева.
В-пятых, оно не является упорядоченным, т.е. нельзя сравнить два произвольных ментальных объекта.
Кроме того, р-адической модели присуща нелокальность, только не в физическом пространстве Rm, а в пространстве Qp.
Поскольку всякий объект в физическом пространстве Rm связан с физическими точками этого пространства, то он обязательно связан с некоторым р-адическим деревом пространства Qp. Каждое такое дерево – это смысловое поле этого объекта, сопряженность в общей иерархии объектов со смыслами, находящимися выше него.
В своей работе «И Слово стало плотию» [9] я привел для физической точки, например, пять иерархически связанных уровней, начиная с клетки. Их может быть и больше.
Человек, являясь физическим объектом, связан со всеми этими смысловыми уровнями. Он, можно сказать, слово, идея, в общем тексте Вселенной. Своими действиями он может отражать свой р-адический смысл, а может искажать. Такое своеволие связано с тем, что человек, управляя инверсией внешнего во внутреннее, а также саморекурсией, использует свойства субстанции Отображения, которая является основой объектов р-адического пространства. Человек, с одной стороны, есть определенная идея, слово и потому определен в своей деятельности и намерениях, а с другой, - он может управлять субстанцией, которая является основой этих смыслов. Он может действовать не только в рамках пространства своего общественного тела, не только на уровне смыслов Биосферы, но и Вселенной, как всей проявленной материи, Космоса, как всей оформленной материи, и М
iра, как Космоса и субстанции Отображения. Человек не просто космическое существо, связанное со всеми смысловыми уровнями физической точки, человек – деятельный космический субъект, влияющий на все уровни космической иерархии, а потому несущий космическую ответственность. Если человек осознанно мыслит, например, на уровне Биосферы, т.е. в иерархии смыслов и организации физической точки поднимается на уровень выше организации отдельного живого существа или рода, то действия его часто идут в разрез с действиями его соплеменников, а его деятельность в р-адическом пространстве влияет на смыслы существования Биосферы и всех на ней живущих. Степень этого влияния зависит от многих факторов, в том числе от степени слияния индивидуального смысла и смысла, отвечающего бытию Биосферы, от характера механизмов сопряжения изменений в р-адических структурах и физических процессов в Биосфере, клетках, атомах и т.д.Но если р-адический мир и мир физических процессов существует как единое целое, то должно же существовать соответствие между р-адическими структурами и свойствами объектов и процессов евклидового пространства.
Если же объекты природы, в том числе и тело человека так непосредственно связаны с р-адическим пространством – пространством физической точки, то как, в чем эта связь проявляется?
Р-адические числа и фрактальность человека
Связь р-адического пространства и физического мира проявляется в процессах и объектах, имеющие фрактальные свойства.
Например, процесс образование канторовской пыли есть однозначное отображение операций с бинарным лексографическим деревом.
Впервые на связь р-адических чисел с фрактальными множествами и физическими проблемами указал ученик Банаха Станислав Мартин Улам в середине XX века.[10] По его представлениям р-адические числа являются инвариантами процессов бесконечного деления вещества и общей топологией различных областей Вселенной, включая объекты с противоположными свойствами, такими как, например, протон и электрон. Именно он констатировал, что р-адическая топология совпадает с топологией канторова совершенного множества C и может рассматриваться как альтернатива континуальным теориям физики и возможности выражения физически осмысленных величин.
Вывод из его работ состоит в том, что «дальнейшая геометризация физики не может быть осуществлена простым обобщением понятий евклидовой геометрии, так как дифференциальная метрика никогда не отразит существенных свойств непрекращающихся процессов деления, но должна основываться на радикальных изменениях локальной топологии (так как в канторовом множестве).». [11, с.1781-1785].
Как было описано в статье «И Слово стало плотию» [9] каждый из уровней р-адической иерархии физической точки связан с определенным пространством согласования физических процессов в евклидовом пространстве. Поэтому каждый из этих уровней будет связан с фрактальными структурами разных пространственных масштабов. У этих пространственных структур будет разная структура смыслов, как правило отличная от смысла соседней пространственной структуры. Эти, казалось бы, разные смыслы объединяет только смысл иерархически высшей структуры, в которую вписаны эти разные пространственные объекты или образования. И они согласуются этим высшим смыслом и физическими процессами, отвечающими этому смыслу. Понять смысл какой-либо структуры вне вписанности и вплетенности ее в иерархически высшую целостность — это как понять смысл многозначного слова вне контекста предложения или произведения. Можно только угадать.
Итак, существование р-адического и евклидового миров, как единого целого, предполагает существование однозначного соответствия между р-адическими иерархическими структурами физической точки и фрактальными структурами метрического пространства. Поэтому, если мы видим где-то фрактальные структуры, то это означает, что в р-адическом пространстве им соответствуют некие иерархические структуры, смыслы, идеи. И это непосредственно касается и человека, и любого живого существа.
Большую работу по систематизации данных о фрактальных свойствах живых организмов сделали Симонян Г.С., Симонян А.Г.[12-14]
В свое работе «Фрактальность биологических систем», состоящей из 3 частей, они показали фрактальность биополимеров, клеток и клеточных ансамблей, органов и организмов.
Так в работе [12] было показано, что белковая поверхность проявляет двухуровневую организацию. Фрактальная размерность микроуровня колеблется около 2,1, а макроуровня для разных белковых семейств – от 2,2 до 2,8. Было установлено, что ДНК образует складчатую фрактальную глобулу, в которой цепь ни разу не завязывается в узел. Многие выводы этой работы имели основания в исследованиях М.В. Авдеева [15], который изучал классы мономеров (моносахариды, аминокислоты и нуклеотиды), играющие особую роль при образовании живых организмов. Именно М.В. Авдеевым было показано, что белковая поверхность проявляет двухуровневую организацию. Такой вывод им был сделан на основе анализа фрактальных свойств поверхности различных белковых семейств, включая глобулярные белки, ДНК-связывающие белки, однодоменные и двудоменные тРНК-связывающие белки.
В следующей их статье [13] рассматривается пространственная организация клеток и клеточных ансамблей. В частности, указывается, что стадия агрегации гемоцитов двустворчатых моллюсков, морских звезд, морского ежа, клетки эпителия гонады и водных лёгких, а также эмбриональные клетки in vitro проходит как хаотическая фрактальная самоорганизация. При этом, значение фрактальной размерности ансамблей клеток варьирует в пределах 1,7 – 1,8. Показано, что фрактальная размерность нейронов мозга костистых рыб и тихоокеанской кеты варьирует у разных типов нейронов в пределах значений от 1.22 до 1.72. Изучение раковых клеток у человека показало, что их фрактальная размерность однозначно выше, чем для нормальных клеток.
Изучение фрактальности органов и организмов [14] показало, что фрактальная размерность бронхиального дерева у млекопитающих не зависит от размера тела и варьирует в пределах 1,57 –1,59. Фрактальная размерность сосудов сетчатки глаза составляет 1,7 и снижается при старении человека и при осложнениях сахарного диабета. Значение фрактальной размерности кровеносной системы человека находится в пределах значений от 2.5 до 2.6. Также установлено, что мочевыделительная система и желчные протоки в печени имеют фрактальную геометрию.
В последние лет 20 получены доказательства фракталоподобной структуры первичной последовательности ДНК, фрактальные свойства которой зависят не только от видоспецифических и эволюционных особенностей всей молекулы в целом, но и морфофункциональных характеристик отдельных ее элементов.
Уже стали классическими исследования на цитологическом уровне фрактальной морфологии нейронов [16, 17], на молекулярном уровне - динамики активности ионных каналов, фрактальных характеристик биомолекул, в том числе молекул белка [18] и последовательности ДНК. Так в работах [19, 20] показано существование определенного типа фрактального поведения в распределении нуклеотидов ДНК.
Исследование фрактальных структур и процессов не обошли и эпигенетику. Именно с использованием фрактального формализма описывается динамика процессов регуляции генной активности, связанное с цитозиновым метилированием. [21].
Квазифрактальность, которую связывают с процессами самоорганизации, исследовалась на всех уровнях организации живых систем [22, 23]. В последнее время исследуется фрактальная организация ядер мозга животного и человека [24,25]. В статье [24] был представлен фрактальный анализ кластеров вентромедиального и латерального гипоталамического ядер гипоталамуса мозга кошки и человека и показано, что кластеры этих ядер у животного и у человека являются монофракталами, но с разной фрактальной размерностью. При этом оказалось, что сами ядра – мультифракталы. Видовые различия геометрической структуры ядер гипоталамуса проявились: во-первых, в более высокой степени неоднородности структуры обоих ядер у человека по сравнению с животным, а, во-вторых, в более низких значениях средних показателей фрактальной размерности кластеров этих ядер у человека, что, по мнению С.Л. Молчатского, свидетельствует о большей упорядоченности их структуры и меньшей энтропии. Им также было показано [25], что нейронные ансамбли мозга можно представить, как перколирующие фрактальные множества, причем полученные им результаты позволяют причислить рассматриваемые нейронные ансамбли к особому классу фрактальных объектов, называемых асимптотически линейно связными, которые сочетают в себе свойства связности и несвязности, т.е. их можно представить как несвязный набор линейно связных подмножеств. Как здесь не вспомнить о единстве р-адического и евклидового пространства, которое предстает единством вполне несвязного и связного пространства.
Кроме фрактальных структур биополимеров, клеток, органов и организма, т.е. кроме существования их смысла и идеи, существует смысл работы, например, центральной нервной системы. Поэтому ничего нет удивительного в том, что появляются работы по фрактальной теории деятельности центральной нервной системы [26, 27] и ее влиянии на морфогенез внутренних органов [27]
Вот как, по мнению Росмана С.В. и Волкова В.П., происходит деятельность ЦНС: «Итак, сложнейшая цитоархитектоника мозговой ткани обеспечивает взаимодействие, взаимовлияние и взаиморегуляцию клеточных элементов, относящихся к различным популяциям. Клетки глии создают сложную структуру, морфофункционально тесно связанную с нейронами, в результате чего имеют возможность повышать и понижать порог потенциала действия нейрона в зависимости от собственного функционального состояния. Можно предположить, что активизация деятельности глии способствует снижению порога потенциала действия. Уровень этой активизации зависит от прохождения возбуждения по итерационным связям нейронной сети.
В результате этого взаимодействия вокруг нейронов появляются мозаичные структуры нейрофизиологических условий — это и есть фрактальная модель кодирования афферентного сигнала. В результате одни группы нейронов остаются в состоянии покоя, а другие генерируют потенциал действия, передающийся по эфферентным путям. Форма фрактала чётко зависит от вида и свойств поступающей информации, поскольку нейронная сеть условиями онтогенеза и филогенетическими свойствами цитоархитектоники головного мозга «настроена» на создание этих бесконечно разнообразных структур…. Следует особенно подчеркнуть бесконечную сложность создаваемой структуры, конфигурация которой воспроизводит свойства афферентного сигнала как в макро, так и в микромасштабе… афферентная информация создаёт базовый фрактал, в котором заключается вся информация о свойствах внешней среды и внутренних средах организма, контролируемых миллиардами рецепторов, разбросанных по всему телу и содержащихся в органах чувств. Малейшие изменения состояния этих рецепторов в каком-либо органе вызывает изменение формы фрактала, в результате чего возбуждаются уже другие нейронные ассоциации в ЦНС, в результате чего на периферию передаётся изменённый эфферентный сигнал.
Организм начинает только тогда нормально функционировать, когда сложится этот базовый фрактал. В этой связи становится понятным тот факт, почему в эмбриогенезе повторяется филогенез — постепенно совершенствующиеся управленческие структуры воспроизводят, как ступени, базовые фракталы филогенеза вида. Однако как функционирует фрактал? Посылаемый из постепенно усложняющихся управленческих структур, он создаёт «нейрофизиологическую строму», по которой, как по направляющим, начинают выстраиваться дифференцирующиеся клетки органа. Именно фрактал определяет, в каком порядке и как должны располагаться основные функциональные образования. Он может так изменять нейрофизиологические условия, что часть клеток в силу изменений в клеточных мембранах могут попадать либо в особо благоприятные условия, либо в совершенно неприемлемые, в результате чего одни клетки начинают бурно разрастаться, а другие, наоборот, лизироваться (явление апоптоза).» [27]
Но, если у деятельности ЦНС есть особый смысл, который проявляется в виде фрактальности ее деятельности, то и у феномена сознания должен быть свой смысл, а значит ему должна отвечать его фрактальная структура. Это уже начинают осмысливать. Так в работе Г.В. Паршиковой «Фрактальный подход к феномену сознания» [28] сознание человека предстает в виде сосуществования «информационной компоненты субъекта и квалитативной составляющей, как феноменологического основания ментальной репрезентации реальности, т.е. сводится к знаменателю фрактала». В статье показано, что самоподобие, как основной принцип фрактальности, заложено в основе языка и любых ментальных конструкций, а квалитативные, т.е. качественные, состояния с разнообразными субстанциональными смыслами, выступая связующим звеном между вещью и ее представлением, проявляют фрактальные особенности.
Если мышление – это способность субстанции к инверсии системных свойств, то сознание - способность отображения системной инверсии, а самосознание – ее фиксации [29]. Дискретное сознание человека – это отображение инверсии с помощью категорий, создание категориального инверсионного зеркала, с помощью которого происходит рекурсия, т.е. обратная ссылка на самого себя. Сознание – не уникальное, но космическое явление. Достаточно, чтобы где-то возник субстрат, с помощью которого возможно было бы отобразить системную инверсию, а затем и зафиксировать её. Сейчас мы пока знаем, что это мозг не только человека, но и других живых существ. Но уже квантовая запутанность трех частиц, которую экспериментально продемонстрировали в 2014 г.[30], позволяет говорить об отображении инверсии двух в третьей, когда воздействие на одну из частиц оказывает влияние на параметры двух других. В этом случае абсолютно неважно, какая из двух частиц, на которые не было оказано внешнее воздействие, является субстратом отображения.
Если человек – его тело, сознание – есть определенная идея, смысл в р-адическом пространстве, то и Вселенная, в которую вписан человек, также должна иметь свою идею, а значит, фрактальные структуры. Сейчас существует целая научная школа, которая занимается фрактальными структурами Вселенной. В частности, интересна обзорная работа
J.K. Yadav [31], в которой показано, что значительная часть статистического анализа указывает на наличие фрактальной природы в небольших масштабах с переходом к однородному распределению галактик. Идет изучение фрактальной структуры всех объектов Вселенной и самой Вселенной, которую на любом уровне можно представить как чередование кластеров и пустот. В обширной монографии «Фрактальная структура Вселенной» [32] петербургского космолога Юрия Барышева и Пекка Теерикорпи из Финляндии утверждается, что в обзорах красных смещений фрактальность распределения галактик уверенно выявляется до масштаба 100 мегапарсек, а неоднородность прослеживается до 500 мегапарсек и более. В этой же монографии приводятся примеры фрактальной размерности периметров межзвездных облаков и т.д.Таким образом, человек, являясь всеми своими органами, системами, клетками, биомолекулами и процессами фракталоподобным движущимся телом, а значит иерархической системой смыслов, в то же время является частью глобального смысла, Идеи, которой живет вся Вселенная, частью которой является солнечная система и наша планета Гея с биосферой.
Любой объект Вселенной, хотим мы того или нет, является одномоментно и пространственно-временным телом, и сложной иерархической р-адической структурой, несущей в себе не только смысл, идею объекта, но и логику вплетения его в процессы, частью которых он является.
Человек – это не просто социальное существо, действующее в пространстве и во времени, человек – это космический актор, имеющий смысловую связь через р-адическое пространство со всеми процессами во Вселенной и могущий влиять и влияющий на них. Человек, как человек духовный и мыслящий, это, прежде всего, свободное р-адическое существо, имеющее возможность выбирать смыслы своего существования, логику своего смыслового развертывания.
Человек – это не просто осознающий себя смысл, а идея, которая в своем саморазвитии может подняться по р-адической иерархии на уровень общего Замысла. Это - путь обожения, путь избавления от частности, разделенности и противопоставления, путь, который человек может пройти, только устремившись всем своим естеством к общему Замыслу, к Богу. Обожение есть непрестанное действие, не только в ментальном, р-адическом пространстве, устремление человека к Богу, нравственное уподобление Ему, но и непрестанное подтверждение этого устремления в поступках:
«Будьте святы, потому что Я свят». (1Пет. 1:16)
1. История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 88—93.
2. Николя Бурбаки. Архитектура математики. Очерки по истории математики. — М.: Иностранная литература, 1963. — С. 38.
3. Фейнман Р. Характер физических законов. — Изд. 2-е. — М.: Наука, 1987. — С. 152—153. — 160 с. — (Библ. Квант, выпуск 62).
4. Татур В.Ю., Р-адические числа, ультраметрика и ментально-вещественный мир //«Академия Тринитаризма», М., Эл № 77-6567, публ.23820, 12.10.2017
URL: http://www.trinitas.ru/rus/doc/0001/005c/00012019.htm
5. Владимирова В.С., Волович И.В., Суперанализ, Дифференциальное исчисление// ТМФ, 1984, т.59, №1, с.3-27
6. Владимирова В.С., Волович И.В., Суперанализ, Интегральное исчисление// ТМФ, 1984, т.60, №2, с.169-198
7. Владимирова В.С., Волович И.В., Р-адическая квантовая механика// Доклады АН СССР, Физика, 1988, т.302, №2, с.320-322.
8. Хренников А.Ю., Моделирование процессов мышления в р-адических системах координат, М.,2013
9. Татур В.Ю., И Слово стало плотию // «Академия Тринитаризма», М., Эл № 77-6567, публ.17813, 27.12.2012
URL: http://www.trinitas.ru/rus/doc/0001/005a/00011245.htm
10. Улам С. Нерешённые математические задачи. – М.: Наука, 1964.
11. Augenstein B. Links Between Set Theory and Physics// Chaos, Solitons and Fractals. V.7. N 11, 1996. P.1761-1798.
12. Симонян Г.С., Симонян А.Г. Фрактальность биологических систем. I Фрактальность Биополимеров
// Успехи современного естествознания, №11, 2015 с. 93-9713. Симонян Г.С., Симонян А.Г. Фрактальность биологических систем.
II Фрактальность клеток и клеточных ансамблей// International journal of applied and fundamental research, № 3, 2016, с268-27114. Симонян Г.С., Симонян А.Г. Фрактальность биологических систем.
III Фрактальность органов и организмов// International journal of applied and fundamental research, № 3, 2016, с.272-27615. Авдеев М.В. Изучение фрактальных свойств поверхности белков : диссертация ... канд. Физ.-мат. Наук. – Дубна,2002. – 102 с.
DOI:10.1016/j.gde.2012.01.006
16. Jelinek H. F., Fernandez E. Neurons and fractals: how reliable and useful are calculations of fractal dimensions?// J. of Neurosci. Methods, 1998, vol. 81, pp. 9–18.
URL: https://www.sciencedirect.com/science/article/pii/S0165027098000211
https://doi.org/10.1016/S0165-0270(98)00021-1
17. Schierwagen A. Neuronal morphology: Shape characteristics and models// Neirofi ziologiya/Neurophysiology, 2008, vol. 40, pp. 310-315.
DOI: 10.1007/s11062-009-9054-7
18. Banerji A., Ghosh I. Fractal symmetry of protein interior: what have we learned? // Cell. Mol. Life Sci.,2011, vol. 68, pp. 2711–2737,
doi: 10.1007/s00018-011-0722-6.
19. Codling E. A., Plank M. J., Benhamou S., Random walk models in biology // Journal of The Royal Society Interface. 2008. Vol. 5(25). P. 813–834.
https://doi.org/10.1098/rsif.2008.0014
URL: https://royalsocietypublishing.org/doi/10.1098/rsif.2008.0014
20. Fudenberg G., Mirny L. A., Higher-order chromatin structure: bridging physics and biology // Current opinion in genetics & development. 2012. Vol. 22. P
. 115–124.21. Тюнин А.П., Каретин Ю.А., Киселев К.В., Анализ изменения автокорелляционной функции цитозинового метилирования ДНК в составе генов стильбен синтаз в культуре клеток винограда амурского Vitis amurensis Rupr. // Вестник КрасГАУ. 2013. № 12. С. 108–113.
22. Goldberger A. L., Amaral L. A., Glass L. et al. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals.// Circulation, 2000, vol. 101, no. 23, pp. 215–220.
URL: https://www.ahajournals.org/doi/full/10.1161/01.cir.101.23.e215
https://doi.org/10.1161/01.CIR.101.23.e215
23. Thistle M. E., Schneider D. C., Gregory R. S. et al. Fractal measures of habitat fragmentation: maximum densities of juvenile cod occur at intermediate eelgrass complexity.// Mar. Ecol. Prog. Ser., 2010, vol. 405,
pp. 39–56.https://www.jstor.org/stable/24873878
DOI
: 10.3354/meps0851124. Молчатский С.Л., Фрактальная организация ядер мозга животного и человека// Самарский научный вестник, 2014. № 2(7), с.77-79
25. Молчатский С.Л., Топологическая и динамическая характеристики нейронных ансамблей мозга как перколирующих фрактальных множеств//
Siberian Journal of Life Sciences and Agriculture, Vol 9, №4, 2017, с.96-105DOI: 10.12731/wsd-2017-4-96-105
26. Иванов Л.Б. Прикладная компьютерная электроэнцефалография. — М.: Антидор, 2000. — 256 с.
27. Росман С.В., Волков В.П. Фрактальная теория деятельности центральной нервной системы и морфогенез внутренних органов// Universum: Медицина и фармакология: электрон. научн. журн. 2015. № 1 (14).
URL: http://7universum.com/ru/med/archive/item/1866
28. Паршикова Г.В., Фрактальный подход к феномену сознания // Философия и культура 4(88), 2015, с. 505-512, DOI: 10.7256/1999-2793.2015.4.14642
29. Татур В.Ю., Отображение как Субстанция единства Космоса и Человека // «Академия Тринитаризма», М., Эл № 77-6567, публ.17797, 21.12.2012
URL: http://www.trinitas.ru/rus/doc/0001/005a/00011244.htm
30. C. Erven, E. Meyer-Scott, K. Fisher, J. Lavoie, B. L. Higgins, Z. Yan, C. J. Pugh, J.-P. Bourgoin, R. Prevedel, L. K. Shalm, L. Richards, N. Gigov, R. Laflamme, G. Weihs, T. Jennewein & K. J. Resch, Experimental three-photon quantum nonlocality under strict locality conditions// Nature Photonics, 2014, volume 8, pages292–296
URL: https://www.nature.com/articles/nphoton.2014.50
31. Jaswant K. Yadav, Reviewing the multifractal nature of clustering of galaxies in the Universe// International Journal of Advanced Research in Computer Science, Volume 8, No. 7, July-August 2017,943-947
DOI: http://dx.doi.org/10.26483/ijarcs.v8i7.4461
32. Ю.В. Барышев и П. Теерикорпи, Фрактальная структура вселенной. Очерк развития космологии, САО РАН, Нижний Архыз, 2005
В.Ю. Татур, Р-адический человек // «Академия Тринитаризма», М.,
|
|