Аннотация¹. В статье сделана попытка понять сущность кривизны пространства-времени в ОТО. Для выяснения физического смысла используется метод отображения, опирающийся на аналогию с философскими категориями «явление-сущность-наблюдатель». Показано, что криволинейное пространство-время не существует самостоятельно без Евклидова пространства. Показано также, что интерпретация явления, называемого «Большой Взрыв», некорректна. Опираясь на метод отображения, доказан пятый постулат Евклида.

Введение

Пространство, как и время, для нас не является материальным. К классическим свойствам пространства мы всегда относим непрерывность, безграничность, однородность и изотропию пространства. Мы всегда отождествляем пространство с геометрией трехмерного пространства, в которой материальные тела не влияют на свойства пространства. С появлением ОТО наше понимание о пространстве изменилось.

Уже не первый год идет обсуждение следствий ОТО. Некоторые аспекты теории «Большого взрыва», «черные дыры», «темная материя» и т.д. не всегда отвечают здравому смыслу, логике наших суждений и обыденным представлениям. Этому есть свои причины. Трудно поверить, что маленькая неточность в геометрии, возникшая еще в начале 19 века, так сильно отразится на физике. Источник ошибки кроется в содержании понятия «кривизна пространства». Что это такое «кривизна пространства» и как ее измерить методом «циркуля и линейки»? Попробуем разобраться.

Мы будем рассматривать только вопросы геометрии пространства, и практически не будем обсуждать содержание физических гипотез, которые привели к возникновению новых понятий и представлений в физике. В частности мы не будем обсуждать очень сомнительную гипотезу об эквивалентности гравитационной и инерциальной масс.

1.Трехмерное пространство

1.1 Введение кривизны

Мы рассмотрим ради наглядности кривизну в трехмерном пространстве. Современные физики и математики строят криволинейное пространство простым способом. Пусть, например, имеется некоторое трехмерное пространство. Ученые задают метрический тензор второго ранга, g_ik который описывает криволинейные свойства исходного трехмерного пространства. Кажется, что здесь нет никаких «подводных камней».

Однако если посмотреть внимательно, то можно увидеть скрытую проблему. Введенный нами метрический тензор g_ik зависит от x, y, z, т.е. g_ik(x; y; z). Независимые переменные x, y, z принадлежат трехмерному Евклидову пространству, которое существовало до введения метрического тензора. Итак, метрический тензор вводится не в «пустое» пространство. Тензор вводится в Евклидово пространство.

Дальше имеет место следующее обстоятельство. Как только физики начинают изучать и описывать свойства криволинейного пространства с метрикой g_ik, они «забывают» о существовании Евклидова пространства. Эта принципиальная ошибка появилась более 200 лет тому назад и превратилась в предрассудок, в догму.

1.2. Философия геометрии

В математике формальная логика есть метод доказательства и критерий его проверки. Если в рассуждениях «выпадают» логические звенья, если вместо аргументов мы опираемся на интуицию, тогда доказательство превращается в обычное субъективное мнение.

Вот и в предыдущем параграфе при введении g_ik(x; y; z) отсутствуют звенья, которые лишают процедуру введения метрического тензора (и криволинейного пространства, соответственно) доказательной силы. Мы начнем все по порядку.

Шаг 1. Начнем с вопроса: в какое пространство мы намерены ввести метрический тензор g_ik(x; y; z)? Мы задали для определенности трехмерное пространство.

Шаг 2. Откуда появились переменные (x; y; z). Мы пока не вводили метрический тензор, и мы понятия не имеем о самом 3-мерном пространстве. Оно может быть криволинейным или Евклидовым. Здесь имеет место неопределенность, которую мы должны разрешить.

Шаг 3. Итак, мы имеем независимые переменные (x; y; z). Будем для простоты считать масштаб вдоль этих линий одинаковым. Это «прямые линии» или нет? Образуют ли они ортогональную «сетку» Евклидова пространства? Пока мы вынуждены предложить гипотезу. Других вариантов мы не усматриваем. Трехмерное пространство является Евклидовым, а не каким-либо произвольным криволинейным пространством.

Шаг 4². Теперь в это пространство мы вводим метрический тензор g_ik(x; y; z). Как это понять? Евклидово пространство после введения метрического тензора вдруг искривилось? Оси (x, y, z), введенные ранее, утратили свою прямолинейность и ортогональность? Если утратили, то по какой причине? Это произошло благодаря нашему субъективному желанию и выбору нужного метрического тензора g_ik(x, y, z)?

Конечно, трехмерное Евклидово пространство сохранилось. Но теперь внутри этого Евклидова пространства «вольготно расположилось» криволинейное пространство, описываемое метрическим тензором g_ik(x, y, z). Компоненты этого тензора выражены через переменные (x, y, z) Евклидова пространства. Такой результат существенно влияет на интерпретацию физических явлений, например, в ОТО.

1.3. В поисках философской аналогии

В философии физики есть такие категории: «явление-сущность-наблюдатель³». В физике наблюдатель познает сущность, исследуя набор явлений. Он воспринимает явления с помощью органов чувств или приборов. Информацию о явлениях он получает благодаря «переносчику информации». Таким переносчиком могут служить, например, световые или акустические волны. Эти волны, доставляя информацию к наблюдателю, могут искажать ее содержание из-за условий распространения.

Можно ли в геометрии пространства использовать аналогичные философские категории? Можно, если с определенными ограничениями осторожно применять аналогию для анализа связей и отношений в геометрии. Здесь философия, оперирующая общими понятиями, подобна в определенном смысле топологии, которая тоже опирается па идеализированные, обобщенные понятия.

Аналогия. Пусть мы имеем два независимых друг от друга трехмерных Евклидовых пространства: E_A(x,y.z) и E_B(u,v.w). Допустим, что с помощью некоторого оператора преобразования пространства с его координатами мы можем отобразить трехмерное пространство E_B(u,v.w) на внутренность пространства E_A(x,y,z). Аналогия показана на рис.1. Обозначим оператор преобразования, как H* на Рис. 1.

Роль переносчика информации играет оператор Н* , который отображает пространство ЕВ внутрь пространства ЕА. Роль явления выполняет отображение. Роль «наблюдателя», который регистрирует явление, играет гипотетический наблюдатель в пространстве E_A(x,y.z). Для нас важно, чтобы пространство E_B(u,v.w) отображалось в E_A(x,y.z) как криволинейное пространство

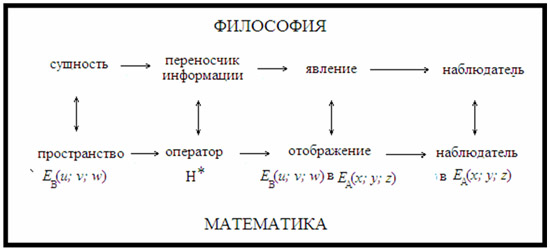
Рис 1

Здесь роль отображаемого объекта (аналог «сущности») играет пространство E_B(u,v.w)..

Раскроем оператор H*:

u = H_u(x, y,z); v = H_v(x, y,z); w = H_w(x, y,z)

Пусть u = const; v=const и w = const внутри пространства E_В. В пространстве E_В эти поверхности образуют три семейства ортогональных плоскостей. В пространстве E_A мы получаем семейство «криволинейных» поверхностей, которые в общем случае могут быть не ортогональными. У нас сейчас нет необходимости вводить какие-либо специальные требования⁴ для оператора H*. Оператор реализует отображение в одном направлении и требование «взаимной однозначности» преобразования не нужно. Нам важно, чтобы отображение было гладким и дважды дифференцируемым. Обозначим отображение пространства E_B(u,v.w) внутрь пространства E_A(x,y,z) как

E_BA(x,y,z) = H*E_B(u,v.w)

Итак, мы видим, что внутри Евклидова пространства E_A появилось криволинейное отображение пространства E_B(u,v.w), т.е. E_BA(x,y,z) = H*E_B(u,v.w).

Пусть метрический тензор этого криволинейного пространства есть g_mn(x,y.z). Если метрический тензор g_ik, введенный ранее в параграфе 1, равен метрическому тензору g_mn (g_ik = g_mn), тогда мы можем считать оба криволинейных пространства эквивалентными. Они могут отличаться только линейными членами, вторые частные производные которых равны нулю. Эти члены не имеют для нас принципиального характера, поскольку кривизна пространства от них не зависит.

Таким образом, нашу гипотезу об исходном трехмерном Евклидовом пространстве, в которое мы описали криволинейное пространство, описываемое метрическим тензором g_ik(x; y; z), можно считать справедливой.

1.4. Первые выводы

Первые выводы противоречат сложившимся представлениям.

Любое трехмерное пространство изначально является Евклидовым. В нем всегда можно ввести Декартову систему координат с ортогональными осями.

Обобщение. Любое N мерное пространство изначально является Евклидовым. Оно не может быть криволинейным.

Криволинейное пространство не может существовать самостоятельно. Оно может существовать только внутри Евклидова пространства. Уберите экран в кинотеатре, и вы не увидите фильм. Уберите Евклидово пространство, тогда криволинейное пространство исчезнет!

Кривизна пространства не является абсолютной величиной. Кривизна есть относительное понятие. Величина кривизны пространства определяется по отношению к Евклидову пространству, внутри которого существует данное криволинейное пространство.

Эти выводы можно распространить на пространства с разным числом измерений N = 2, 3, 4 …

***

2. Псевдоевклидово пространство

Проведенные выше рассуждения и выводы легко обобщаются на случай Евклидовых пространств N измерений. Мы рассмотрим пространство четырех измерений (N = 4), распространив на него полученные выводы. Если мы представим четвертую переменную как мнимую координату (x₄ = ict), то получим псевдоевклидово пространство. Формально оно мало отличается от четырехмерного Евклидова пространства Е(r; t). Пространство Минковского можно рассмотреть аналогичным образом.

Мы не ставим перед собой цель дать новую интерпретацию ОТО. Это сложный вопрос. Мы хотим выявить некоторые проблемы, которые возникают из-за «соседства» Евклидова пространства-времени рядом с криволинейным пространством-временем.

Итак, пусть мы имеем псевдоевклидово пространство Е_А(r; t), в котором существует криволинейное отображение некоторого псевдоевклидова пространства E_B(u, τ), которое мы обозначили как E_ВA(r;t) = Н* E_B(u, τ).

Отображение может иметь нестационарный характер и зависеть от времени.

Мы покажем, например, к каким выводам приводит метод отображения при анализе «Большого Взрыва». Допустим, что криволинейное отображение находится внутри сферы бесконечного 4-радиуса, которая расположена в E_ВA(r;t).

Пусть оператор отображения Н* позволяет уменьшать радиус этой сферы во времени до нуля. Криволинейное отображение E_ВA(r;t), будет «сжиматься» в точку перед «неизбежным Большим Взрывом». В рамках ОТО имеет место следующее утверждение. Пространство, время и материя «слипаются» вместе в бесконечно малую точку. Вокруг странная «пустота», не имеющая материи, пространственных размеров и времени.

С позиции отображения пространства подобное утверждение не является корректным. «Точка» находится не в «пустоте». Она всегда находится в исходном пространственно - временном континууме Е_А(r; t), поскольку пространство-время Е_А(r; t) не «деформируется» оператором отображения Н*.

Теперь мы поговорим о материальных объектах, имеющих массу и инерцию. Допустим, что материальные объекты принадлежат Е_А(r; t). С одной стороны, согласно ОТО кривизна пространства и материальные гравитационные объекты имеют взаимную связь. С другой стороны 4-пространство Е_А(r; t) и материальные объекты в нем не зависят от оператора. Следовательно, в случае «сжатия» криволинейного 4-пространства взаимная связь между кривизной и гравитирующими массами теряется.

Пространство-время в отображении «сжимаются» вместе со своей кривизной, а материальные объекты в Е_А(r; t) остаются неизменными. Отсюда следует, что материальных объектов, принадлежащих Е_А(r; t) в Е_B(r; t) не должно существовать принципиально. Они существуют в Е_B(r; t) и должны «транспортироваться» в Е_А(r; t) из Е_B(r; t) вместе с «кривизной»!

Напомним, что отображенные объекты и отображенное криволинейное 4-пространство есть явления. Оператор H* деформирует материальные объекты и «одевает» их в «криволинейную пространственно-временную оболочку» только при отображении E_B(u,τ) в Е_А(r; t).

Таким образом, все «депортированные» из E_B(u,τ) в Е_А(r; t) инерциальные материальные тела.представляют собой «отображения» каких-то реальных «прототипов», существующих в E_B(u,τ). Мы - люди не являемся исключением и имеем своих «прототипов-двойников». Это не «загробный мир»!

Вы можете представить себе, что вы есть «искаженное отображение» вашего «неискаженного прототипа-двойника», который бродит где-то далеко-далеко от вас в E_B(u,τ)? В отличие от вас, его нельзя «сжать в точку», т.е. он не подвержен действию оператора и, соответственно, воздействию «Большого Взрыва»!

Мы видим, что даже на первом этапе переосмысления явлений физики встретят много трудностей при интерпретации явлений ОТО. Мы не будем больше выходить за пределы геометрии и обсуждать эти вопросы. Здесь много странного и неясного, выходящего за пределы здравого смысла. Такие проблемы должны обсуждать физики-теоретики, философы, теологи и писатели-фантасты.

***

Допущение, сделанное в Части 1.2, является корректным. Мы можем выводы распространить и на двумерное пространство (плоскость). Воспроизведем эти выводы для плоскости:

Любое двумерное пространство всегда изначально является Евклидовым. Не существует геометрических методов («циркуль-линейка-карандаш») для измерения внутренней относительной кривизны различных участков плоскости.

Криволинейное двумерное пространство на плоскости не может существовать самостоятельно. Криволинейное пространство на плоскости может быть только как нелинейное отображение некоторого другого Евклидова пространства на исходное Евклидово пространство.

По этой причине мы не можем рассматривать 5-й постулат Евклида, как гипотезу, которую Лобачевский или Гаусс могли заменить другой гипотезой. Пятый постулат Евклида, формулировка которого в разных источниках приводится по-разному, с самого начала вызвала спорт и желание перевести его в разряд теорем путем построения обоснованного доказательства. Кстати, нередко его подменяют другим выражением, на самом деле придуманным Проклом и известным, как аксиома Плейфера.

Оно гласит: на плоскости через точку, не принадлежащей данной прямой, возможно провести одну и только одну прямую, параллельную данной. Эта аксиома теперь не является гипотезой и её не нужно доказывать!

Заключение

Итак, анализируя способ построения криволинейного пространства, мы обнаружили «застарелую» ошибку геометров. Эта ошибка существует порядка 200 лет. У ученых при построении криволинейных пространств в исходном Евклидовом пространстве после построения «забывают» о том, что Евклидово пространство не исчезло!

Это обстоятельство не позволяет дать правильную и логически строгую интерпретацию явлений в рамках ОТО. Объяснения явлений в рамках ОТО похожи на фантазии или схоластику, оторванную от реальности. Уже сейчас мы можем сказать, что большинство объяснений явлений в рамках современной ОТО, Космологии, Астрофизики не являются корректными и нуждаются в кардинальном пересмотре. Ученые должны приводить доказательные объяснения явлениям, а не пугать обывателя фантазиями и «страшилками», опирающимися на застарелые неверные представления («Большой Взрыв», «Темная материя», «Черные дыры» и т.д.).

Добавление. (В.А. Кулигин).

Здесь я хочу высказать пессимистическую мысль. Все возможные попытки «реанимации» ОТО бессмысленны. ОТО, как и СТО, изначально были «недоношенным ребенком» и противоречили классическому материалистическому мировоззрению. Подобные «теории» могут рождаться только в период «философского (мировоззренческого) кризиса». Относительно недавно вышла книга Б.Штерна «Прорыв за край света⁵».

Аннотация. В книге рассказывается о том, как возникла наша Вселенная — о первых мгновениях существования, определивших ее дальнейшую судьбу. Теперь мы в общих чертах знаем об этом благодаря двум революциям в космологии, произошедшим за последние сто лет, — созданию Общей теории относительности, появлению теории космологической инфляции, блестяще подтвержденной недавними наблюдениями. Книга содержит интервью с соотечественниками, внесшими решающий вклад в становление этой теории. В книге есть дополнительная веселая научно-фантастическая сюжетная линия: развитие космологии разумных существ подледного океана спутника Юпитера Европы. Она иллюстрирует процесс познания мира на более простом материале и позволяет читателю развеяться. Книга рассчитана на широкий круг читателей, хотя уровень сложности материала сильно отличается от главы к главе. Автор исходил из принципа: «Любой читатель — от школьника до профессионального физика — сможет найти в книге то, что ему понятно и интересно». Книга написана живым языком, без чрезмерной серьезности и изобилует «лирическими отступлениями» о смысле и роли науки.

Награды за книгу:

Диплом финалиста премии «Просветитель» (2014)

Премия имени Александра Беляева (2015)

После публикации этой книги я писал в газету ТРОИЦКИЙ ВАРИАНТ проф. Б.Штерну и изложил результаты наших исследований [5]. Я прекрасно понимал, что Б.Штерну и В. Рубакову будет не очень приятно узнать об ошибке. К сожалению, ответа на моё обращение не последовало. С истиной можно не церемониться! Со своей стороны я могу сказать, что книга Б. Штерна хорошая фантастика (или схоластика), но к науке не имеет никакого отношения.

Сколько подобных статей книг написано! Сколько защищено диссертаций! Мне не жаль тех, кто ошибается, но упрямо и догматически «увяз» в своем самомнении. Мне жаль лесные угодья. Сколько хороших деревьев вырублено только для того, чтобы публиковать подобную околонаучную схоластику!

Конечно, это мизер по сравнению с хищнической вырубкой лесов России Китаем! Я неоднократно писал в РАН и в организации РАН об ошибке геометров. К сожалению, ни одного ответа на обращения я не получил. Сторонники ОТО в РАН оказались «короедами-догматиками».

Ссылки:

1 A.Chubikalo, A Espinosa, V.Kuligin Spatial curvature as a distorted mapping of Euclidean space, Boson Journal of Modern Physics (BJMP) Vol. 4, Issue 2, ISSN 2454-8413 , October, 13, 2018.

2 М.В. Сажин. Теория относительности для астрономов.

http://www.astronet.ru/db/msg/1170927/index.html

3 В.А. Кулигин. Материализм и теория относительности.

http://www.sciteclibrary.ru/texsts/rus/stat/st6933.pdf

4. Б. Штерн Прорыв за край света. Издательство «Троицкий вариант», 2014 год. 2014 год, ISBN 987−5-89 513−345−3.

5. В.F. Кулигин Черные дыры в тёмной материи.

http://www.trinitas.ru/rus/doc/0016/001d/00162448.htm

Примечания

¹ Данная статья есть свободный перевод с сокращениями работы, опубликованной в американском журнале [1].

² См., например, [2]

³ Связь философских категорий «сущность-явление-наблюдатель» изложено в [3].

⁴ Мы рассматриваем одностороннее отображение из Е_В в Е_А. Обратное отображение, т.е. отображение E_A(x,y.z) внутрь пространства E_B(u,v.w) мы не рассматриваем. Такое отображение было бы необходимо при анализе взаимодействия материальных объектов этих пространств между собой.

⁵ Борис Штерн, докт. физ.-мат. наук, ведущий научный сотрудник ИЯИ РАН, Научный редактор: Валерий Рубаков, академик РАН, главный научный сотрудник ИЯИ РАН.