Область науки, использующая такие понятия, как нелинейная динамика, хаос, фракталы, в последние годы обострила интерес к основам и самым животрепещущим проблемам естествознания¹. Здесь — и структура мироздания; пространство и время; место и роль детерминизма и случайности в описании явлений природы; предсказуемость и смысл законов физики; синергия и процессы эволюции материи; соотношение между живым и косным веществом; физическое и психическое; язык и мышление. Каждая из этих тем необъятна и интригующа. По мере продвижения в исследовании материала по любому направлению быстро улавливаются различные взаимосвязи, рождающие ассоциации, и, начиная с некоторого этапа, уже трудно различить верх и глубину, основания и выводы исследования — возникает ощущение симфонии, целостной картины мира.

В настоящей работе мы сосредоточим внимание на новых представлениях, связанных с фрактальными (дробными) множествами². Наша цель — понять, что поддерживает в тысячелетнем опыте человечества саму идею фрактальной геометрии природы и как она отражена во взглядах на структуру мироздания. Иными словами, насколько естественна, органична эта область, или же фракталы всё ещё представляют собой своего рода патологию в системе понятий науки?

Для начала обратимся к самому понятию фрактальное множество. Существуют его различные определения, которые до сих пор не сведены в общепринятую краткую формулировку. Наиболее устойчивым и интуитивно содержательным является описание, включающее все или большинство из следующих свойств:

1) Вплоть до произвольно малых масштабов прослеживается тонкая, запутанная структура, как бы составленная из деталей. Непрерывное увеличение разрешающей способности наблюдения позволяет постоянно обнаруживать детали строения, никогда не сводимые к одной-единственной точке.

2) Организация слишком нерегулярна, чтобы быть описанной традиционным аналитическим или геометрическим языком, и не удовлетворяет каким-либо простым соотношениям, уравнениям или неравенствам.

3) Часто прослеживается тот или иной вид самоподобия (скейлинг), то есть схожесть картин, которые возникают в поле зрения при увеличении разрешающей способности наблюдения; независимость их от масштаба. Самоподобие может быть геометрическим, статистическим, а также — по идентичности способов описания структуры множества.

4) Вблизи каждого элемента множества имеется большое число других, разделённых промежутками разной длины. В ограниченной области фрактал содержит их бесконечное число.

5) Обычно фрактальная размерность множества (d) больше его топологической размерности³ и является дробным числом, заключённым между 1, 2 или 3. Фрактал, как говорят, «странно устроен».

6) Множество определяется алгоритмически просто и может быть получено как предельное множество (аттрактор) простых нелинейных зависимостей, описывающих динамические системы и процессы.

7) Множество имеет естественное «происхождение», и его природа, субстанция фрактального объекта, может быть самой разнообразной — косное или живое вещество, материальные, смысловые, языковые формы. Такие объекты встречаются часто «вдали от равновесия» — в неравновесных, нестационарных явлениях, в сфере действия нелинейных, циклических, так называемых автореферентных процессов (англ. self-reference — самоприменимый), в которых области проявления причин и следствий совпадают (в них исчезают различия между аргументами и функциями преобразований — в этом суть понятия нелинейности).

Наиболее известными представителями фрактальных множеств являются графики непрерывных, но всюду не- дифференцируемых функций ( то есть «всюду ломаных» непрерывных линий, не имеющих касательных ни в одной своей точке), а также фигуры, границы которых и даже их внутренность образованы такими же «ломаными» кривыми.

Вообще вездесущесть, «универсальность бытия» фракталов имеет прямое соответствие в математике. Из математического анализа известно, что «всюду ломаные», иррегулярные функции составляют подавляющее большинство по сравнению с непрерывными гладкими кривыми — идеальным вариантом, то есть дифференцируемость есть нетипичное, частное свойство функций и траекторий (рис. 1). Далее, из раздела математики— топологии известна универсальная кривая Серпинского (рис. 2а), называемая во фрактальной теории ковром Серпинского, которая содержит эталоны форм всех плоских кривых. Тем же свойством обладает континуум Менгера (рис. 26) — обобщение на пространственный случай кривой Серпинского.

Из математического анализа опять же известно, что любое компактное метрическое пространство («наука начинается тогда, когда начинаются измерения!» — возможно введение метрики) есть непрерывный образ канонического фрактала — Канторова триадного совершенного множества (рис. 2в). С теоретико-числовой точки зрения, единственной ближайшей альтернативой полю действительных чисел является поле так называемых р-адических чисел, которое как раз и имеет фрактальную структуру⁴. Этот факт особенно важен. Дело в том, что множества, имеющие структуру полей, отличаются от множеств, являющихся просто набором различных объектов, тем, что на полях возможно построение и применение измерительных процедур, развитие математических теорий и методов. Это значит, что p/адические поля могут послужить построению метрических пространств нового типа и, соответственно, развитию теорий. Поэтому фракталы — далеко не просто коллекция или «зоопарк» красивых фигур, а именно поле взаимосвязанных элементов, поддающихся сравнительным измерениям, как мы увидим далее, — вполне специфическим.

Возникают вопросы. Неужели перечисленные универсальные свойства фракталов, которые первоначально появились как мысленные конструкции, бесполезны для понимания мироустройства и общих закономерностей движения материи, таких как синергия и эволюция? Неужели в общих свой - этим и «пользуется» лишь традиционными математическими структурами, то есть, существует ли в природе, по выражению автора теории самоорганизованной критичности П.Бэка, исключительно «тонкая настройка параметров», соответствующая идеологии дифференциальных уравнений? Может быть указанные универсалии являются ключом к познанию неких общих черт, характеризующих единство мира?

На вездесущесть фрактальной геометрии природы впервые обратил внимание в 70-х годах XX века специалист по теории вероятностей, ныне работающий в корпорации IBM (США), математик Б.Мандельброт. По сей день он является главой наиболее многочисленного направления работ по фрактальным множествам и процессам. Основа этих работ — вероятностно-статистический формализм, который давно и хорошо известен, концентрация внимания вокруг устойчивых распределений — вызывает стойкий скептицизм у учёных физико-математического профиля. Создаётся впечатление, что нарушается известный принцип Оккама: «не умножать сущностей без надобности». Однако, хотя и в методологическом плане данные работы не безупречны, они весьма основательно проработали тему, дав широкий спектр иллюстраций фрактальных объектов и процессов и тесно связав их существование с повсеместно обнаруживаемыми степенными зависимостями частоты встречаемости данного объекта от его размера (N=l^-d — законы Ципфа в лингвистике, Гутенберга-Рихтера в геофизике, Парето в экономике, фликкер-шум и другие; где N — частота, l — линейный размер, d — фрактальная размерность множества).

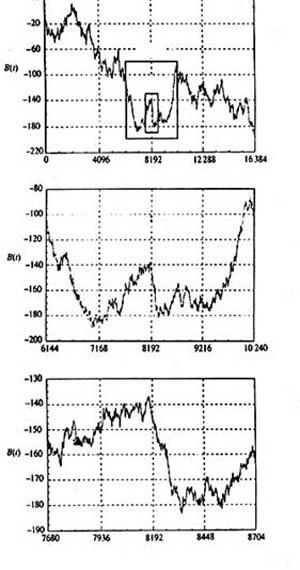
Рис.1. Типичные в природе «всюду ломаные» (недифференцируемые) кривые

Наличие таких зависимостей сейчас можно считать наблюдаемым и экспериментальным фактом, сигнализирующим о преобладании вокруг нас нерегулярной геометрии — фрактальной. Серьёзной заслугой указанных работ следует считать то, что они высветили роль и значение тех известных математических фактов (в частности, отмеченных выше универсалий), которые раньше считались патологическими и использовались лишь для построения контрпримеров. Эти обстоятельства позволили автору данной статьи выстроить классические математические положения, связанные с фрактальной теорией, в систему понятий со своей теорией множеств и логикой, теорией чисел, анализом и физической феноменологией. Все новейшие идеи и выводы теории фракталов так или иначе оказались задействованы и сосредоточены в р-адической, или неархимедовой, математике и в физических представлениях о неархимедовом пространстве-времени. Поясним, что неархимедов мир отличается от привычного прежде всего тем, что там становятся бессодержательными измерения при помощи линейных мер, которые обычно используются в знакомом нам физическом мире, а понятие измерения величин приобретает иное содержание. Математически это означает, что не выполняется так называемая аксиома Архимеда (аксиома измеримости) — одна из основных аксиом классического математического описания явлений. Ощутить естественность необычного неархимедова мира легче, если понять, какие физические процессы составляют его «ткань». Так что перейдём к изложению этой феноменологии.

По-видимому, впервые на множества, которые позже стали называться фракталами, обратил внимание американский математик польского происхождения С.Улам в первой половине XX века. К 1964 году развитие его взглядов, предвосхитивших сегодняшние идеи во фрактальном естествознании, можно суммировать следующим образом. С.Улам задался вопросом о неисчерпаемой сложности микромира и нескончаемом разнообразии макромира, о существовании и роли бесконечностей в физике и о том, почему в таких условиях возможна физика как единая наука. Такое чудо, следует его вывод, не состоялось, если бы, образно говоря, электроны и протоны как противоположности не были бы во многом едины! Это единство суть делимость материи и существование в природе различных процессов деления — ветвящихся процессов. Никакими физическими законами не запрещается их бесконечность. По этой причине возникает подобие самых различных подмножеств универсума физики, которое и является основой построения теории множеств, отражающей единство науки. Но тогда, как совместить противоположности — непрерывность и дискретность, предопределённость и случайность? С.Улам замечает, что процессам деления соответствует топология (строение) пространства-времени p-адического типа, или, что то же, типа Канторова совершенного множества — несчётная совокупность отдельных элементов (точек). На таком множестве сочетание противоположных свойств становится уже возможным: эти множества (дисконтинуумы — дискретные континуумы) не образуют ни непрерывного континуума в обычном смысле, ни множества дискретных неделимых точек. На них любой физический объект, обладающий, например, массой, автоматически оказывается делимым, значит структурированным. В таком мире, построенном на идеях единства материи, не имеет места аксиома фундирования в классической теории множеств (англ. foundation — основание, фундамент), которая устанавливает существование праэлементов, «атомов простоты», «дна элементарности» в каждом множестве. Пространство-время такого бесконечно сложного мира, не только дискретного, но и непрерывного, должно иметь иерархическую структуру, и не существует единственного пути определения однородного пространства-времени, традиционного для физики.

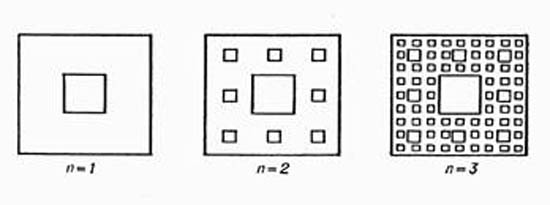
Рис.2а. Ковёр Серпинского

Здесь мы подошли к ещё одной универсалии, присущей фракталам. В рассуждениях С.Улама фрактальные множества предстают как основа единства «многопредметной», разнородной субстанции, «чуда» междисциплинарной науки. Это типично для экономической, экологической, психологической и глобальной проблематик. Ведь природа в своём движении не знает деления на научные дисциплины.

Независимо от С.Улама, но в другой мотивировке, в наши дни идеи p-адического (неархимедова) пространства-времени возникли и стали развиваться в физике микромира, в теории струн. Работа российских математиков подводит итог примерно десятилетнему латентному периоду развития новой физики и сулит дальнейшие перспективы построения физических теорий в мире с новой геометрией. Именно И.В.Воловичем, одним из авторов пионерской монографии[4], был выдвинут и обоснован принцип инвариантности (независимости) физических теорий относительно способа описания числового поля, в данном случае — поля действительных чисел на более широком поле p-адических чисел. Примерно в это же время было показано, что все известные фракталы могут быть получены как различные модельные отображения полей p-адических чисел в привычное физическое пространство[2][4]. Задачи математического описания процессов во фрактальном мире, таким образом, стало возможным решать в p-адическом мире на прочной теоретико-множественной и числовой основе. Это обогатило математику фракталов широким спектром связей с различными разделами классической математики — алгеброй, теорией чисел, логикой, анализом, топологией и теорией множеств.

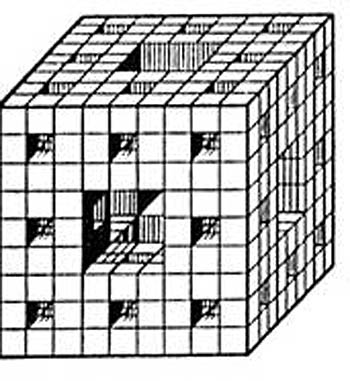
Рис.2б. Континуум Менгера

В качестве теории множеств для фрактальной геометрии следует признать теорию так называемых плохообусловленных множеств (англ. non-well-founded sets). Это как раз те множества, которые появлялись в рассуждениях С.Улама и для которых не выполнена классическая аксиома фундирования — физически отсутствуют «атомы простоты». Математически это означает, что все части любого исходного множества являются по смыслу просто его подмножествами (… ∈ a_n+1 ∈ a_n ∈…. ∈ a₁ ∈ a₀ ∈ A, где ∈ — знак принадлежности), а не неделимыми элементами. Значит каждый фрагмент множества признаётся бесконечно делимым, а понятие материальной точки более не является приемлемым при описании. Именно это и обеспечивает полноценное самоподобие для соответствующих фрактальных объектов, то есть возможность постоянно наблюдать похожие неэлементарные картины, «заглядывая вглубь» объекта. (Отсутствие же достаточно глубокого самоподобия для статических физических фракталов является на сегодняшний день одним из серьёзнейших аргументов критики фрактальной теории.) Теоретически показано, что именно плохообусловленные множества (или гипермножества) имеют самоподобную структуру (это легко уяснить, если записать произвольное нелинейное соотношение в виде: X ∈ {1,X}, где X— множество; или в привычном виде: у =f(x,y) =f(x, f(x, у)) =f(x, f(x, f(x, у))) = ..., где равенство бесконечно разворачивается вправо). Оказывается, что в мире гипермножеств любое нелинейное уравнение имеет решение — в этом математическая суть аксиомы антифундирования (англ. antifoundation — отрицание, неприятие существования какого-либо фундамента). Нетривиальными решениями нелинейных уравнений как раз и объявляются плохообусловленные множества.

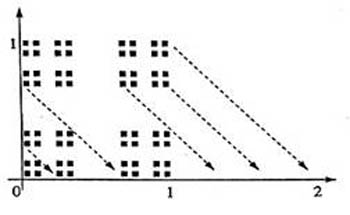
Рис.2в. Отрезок [0, 2] как образ Канторова триадного множества

Мир бесконечных по делимости множеств намного богаче мира традиционно используемых. Можно показать, что в общем случае подмножества плохообусловленного универсума переплетаются и вложены друг в друга, порождая тесную взаимосвязь (или бутстрап; англ. bootstrap — шнуровка) на всём универсуме. Представить себе бутстрап можно, если поставить два зеркала одно напротив другого. Тогда в каждом из них можно увидеть их взаимную, попеременную вложенность. Усложнив эту конструкцию большим количеством зеркал, чтобы любое из них отражалось в каждом, можно попытаться в полноте ощутить подобное явление. О гипермножествах стоило упомянуть по той причине, что их теория развивалась параллельно с p-адической теорией, но независимо от неё, имея свою, существенно нефизическую область порождающих идей, которые пришли из компьютерных наук, проектирования сложных вычислительных систем, анализа известных логических парадоксов, теории игр, социальной сферы, философии и других «мягких» наук. Было замечено, что в этих областях при анализе проблем постоянно появляются запутанные иерархические схемы и причинно-следственные и семантические цепочки, циклически и нелинейно действующие автореферентные операторы и соотношения, которые невозможно моделировать нелинейными дифференциальными уравнениями, как это принято в физике. Поэтому и был применён обычный для математики приём изменение аксиоматической базы. Так, в сферу приложения идей фрактальной геометрии попал очень богатый, ранее скрытый от её внимания, класс явлений и систем существенно языковой природы.

Кратко расскажем об основах p-адической математики и том мире, который она рисует. Как следует из изложенного, фрактальный и p-адический миры можно считать синонимами. В математику p-адические числа были введены в конце XIX века немецким математиком К.Гензелем по аналогии с полиномами в комплексной области⁵. Оказалось, что числа и функции комплексного переменного во многом ведут себя сходным образом. Подобно тому, как комплексные числа аналогичны векторам на плоскости, p-адические числа представляют аналогию разложения в так называемый ряд Лорана произвольной функции и записываются в виде либо бесконечного ряда по степеням какого-либо простого числа⁶

 

либо в записи, подобной десятичной записи числа, но только с бесконечной «целой» частью, соответствующей положительным степеням  p (x = a_—ma_—m+1...a_—1a₀a₁a₂...a_n..., где a_i ∈{0, 1, 2,...p—1}— цифры, p = 2, 3, 5, ...41, ...137, ... — одно из простых чисел натурального ряда). Поскольку, как видно, р- адические числа бесконечно велики в обычной метрике, то величина такого числа определяется по первому ненулевому члену ряда по формуле:

|x|_p = p^–αm, α>0

Смысл в том, что эта величина обратно пропорциональна степени делимости данного числа на фиксированное простое число р. Чем «большее количество раз» данное число делится на р, то есть чем больше параметр т, тем меньше его p-адическая величина (например: |36|₂ =1/4, |7|₂=1, |137|₂ = 1, |1/64|₂ = 64). Главное отличие так вводимой величины числа заключается в её неархимедовости — в отличие от обычных линейных мер, в невыполнении условия простого сложения (|x₁ + х₂|_р ≤ max{|x₁|_p, |х₂|_p} ≠ |х₁|_p + |x₂|_p). Такое определение величины числа — не просто отвлечённая теоретическая конструкция. Оказывается, что если мы хотим что-либо мерить, строить и развивать количественные оценки и методы, то выбор у нас невелик: либо обычные рациональные числа с обычным модулем (длиной), либо p-адические числа с указанной p-адической величиной (частотой). Это — фундаментальные факты из курса общей алгебры. Нетрудно показать, что упомянутые выше знаменитые «фрактальные» степенные законы есть просто связь его обычной и p-адической мер для каждого физического и языкового объектов (так называемая «формула произведения» в p-адическом анализе). Величина параметра α^-1 в этом случае совпадает с фрактальной размерностью d изучаемого объекта.

Работы последних лет показали, что особенности строения p-адических чисел придают их совокупностям, то есть полям Z_p (m=0) и Q_p (m>0), кластерную⁷, фрактальную структуру. Всё множество натуральных чисел в p-адической норме сжимается до кластера (0 ≤ х ≤ 1). В общем случае поле Z_p (или Q_p) состоит из своих копий

(здесь умножение на степень р означает увеличение степени разрешения наблюдения кластера в р раз). Общее строение легко уяснить из рис. 3. В зависимости от значения параметра а (в определении p-адической величины) могут получаться фракталы самых разных форм. С кластерной структурой корреспондирует представление полей р-адических чисел в виде плохообусловленных множеств. Аналогию можно понять, если записать это множество в «нелинейном», уже знакомом нам виде:

Рис.3. Строение поля Z₇ и его фрактальные образы

Всё, что говорилось о гипермножествах выше, оказывается верным и для р-адических чисел. В частности, взаимосвязь всех его частей обеспечивается взаимным вложением кластеров (см. рис. 3). Такие множества реализуют идею микрокосма, принципа «каждое в каждом». Как видно из определения, множество р-адических чисел представимо в виде дерева с ветвлением на р частей в каждой вершине. Такое дерево иногда называют иерархическим или лексикографическим. Конкретное число получается, если следовать вдоль некоторого выделенного пути по его ветвям, последовательно выписывая цифры в вершинах; каждому пути соответствует определённое число и наоборот (рис. 4). Эти деревья могут мыслиться как эталоны делимости материи, а также как схемы причинно-следственных связей взаимодействия объектов в различных процессах в соответствии с заданным простым числом р, которое играет роль физического параметра. Номер уровня иерархии равен степени увеличения разрешения, с которым наблюдается структура кластеров. Если придать ветвям дерева «равноправный» вид, то получится так называемое дерево Брюа-Титса, которое наблюдается на «поверхности», определяемой концами ветвей исходного дерева р-адических чисел. Это дерево представляет собой наглядный образ фрактальной, или p-адической, «ткани» мира (рис.5). Конечно, рисунок не может передать всей иерархической полноты картины. Видны лишь кластеры, которые при увеличении разрешения, в свою очередь, предстают в виде деревьев. Дерево Брюа-Титса самоподобно в том смысле, что центром мира может служить любая его вершина — нет выделенного масштаба, из любой точки этого дерева мир выглядит одинаково⁸. Простые арифметические действия над р-адическими числами придают законченность р-адическому миру в виде сети, в которой каждая вершина связана с любой другой. Взаимосвязь фракталов и сетей, как оказалось, не просто теоретическое совпадение⁹. Исследование функционирования самой большой на сегодняшний день искусственной сети — Интернет показало фрактальный характер динамики потока заявок.

Итак, мы приходим к ещё одному — сетевому представлению о мироустройстве. Этот мир уже существенно отличается от традиционного Декарта-Ньютонова. Сетевой мир является взаимообусловленным, населённым: любой его объект существует только в связи и за счёт других объектов. В этом мире нет надобности вводить обратные связи — они изначально существуют на всех масштабах. Известно много различных теорий, концепций и гипотез в системных науках и в так называемых «науках о жизни», эмпирически основанных и группирующихся вокруг сетевой картины Мира[6]. В р-адической математике показано, что такой мир в целом имеет форму соленоида, то есть «бублика».

Наконец у р-адической математики есть ещё одна сторона, неразрывно связанная с вышеизложенным. Устройство р-адических числовых полей, или их топология, позволяет рассматривать набор цифр разложения чисел как буквы некоторого алфавита А = {0, 1, 2, ... р—1}. Тогда числа предстают в виде слов — кодов Гензеля, которые группируются в предложения, тексты, формальные языки и теории. Весь мир тогда являет собой гипермножество Z_p = [0, 1, 2, ...p—1]^N. Поэтому р-адические числа пригодны для кодирования информации, описания какой-либо области алгоритмического или языкового характера. Это значит, что в р-адических фракталах, возможно впервые, соединяются материальное, физическое и символьное (языковое) представления о мире. Тема эта слишком сложна и с точки зрения математического описания, по-видимому, ещё не сформирована, поэтому мы обратимся к двум другим сферам — психологии и философии, где аналогии могут быть прослежены. Отметим лишь, что сетевая структура мира объясняет существование и взаимосвязь разнородных по природе объектов — материальных, языковых и связана со «считающей» р-адической наукой. Поэтому становится возможным введение количественных методов изучения взаимодействия общества и внешней среды — ландшафта, экономики, а значит и исследований в русле идей коэволюции — совместной эволюции человека и природы.

Сетевая модель фрактального мира побуждает взглянуть в сторону математического моделирования в психологии. Нелинейность, цикличность мыслительных процессов и сетевая структура мозга были замечены давно, а в последние годы установлена связь динамики этих процессов с явлениями хаоса и фракталами. Одна из отечественных и зарубежных работ близка теме настоящей статьи, так как посвящена анализу основ применения математики в психологии[7]. Эта монография может рассматриваться как прекрасное мотивированное введение в круг вышеописанных понятий, формирующая полноценное р-адическое «плохообусловленное» мироощущение.

Наметим существующие соответствия между, казалось бы, разными областями. Для понимания системности как основы моделирования достаточно обратиться к феноменологии С.Улама. Междисциплинарный характер процесса мышления очевиден, ибо именно оно породило всё многообразие научных дисциплин, представления о дискретности и непрерывности, детерминизме и случайности. Взаимопроникновение, ничем не устранимая связность, а это считается основной трудностью при описании мышления, прямо усматривается из структуры р-адического плохообусловленного мира, где «каждое в каждом». Неаддитивность, то есть не простое, а системное сложение мыслительных актов, также следует из неархимедовости. Основным признаётся то, что мышление есть процесс, но и мир фракталов существует в полной мере лишь вдали от равновесия, иначе говоря — в движении. В монографии особое внимание уделено гипотетической математике, пригодной для моделирования процесса мышления. Считается необходимым, чтобы числовая система несла в себе идею «нестатистической, невероятностной неопределённости» и принципиальной размытости — диффузности. В качестве первой части требования общим местом в литературе видится то, что фрактально-хаотические явления порождаются детерминированными алгоритмами, например, сетевой динамикой, и часто называются «детерминированной случайностью». Обоснованность второй части требования можно видеть из того, что р-адическое число всегда будет наблюдаться с нечётким окончанием (х = а₀ + а₁p + ... + a_k-1p^k-1+ p^kZ_p ). Первые слагаемые есть «чёткая», рациональная составляющая, последнее слагаемое — диффузное «пятнышко», остающееся за пределами разрешающей способности, копия исходного числового поля, представляющая искомую неопределённость. В плохообусловленном мире, где нет изолированных «атомов простоты», приобретает смысл необычное увеличение информации в процессе познания путём «исчерпывания» объекта и его связей с внешней средой.

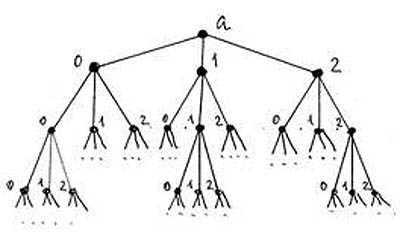
Рис.4. Схема множества р-адических чисел и их дерево (р=3)

 Изложение и исследование параллелей можно в значительной степени продолжить и расширить, если исследовать движения во фрактальном р-адическом мире. Но здесь мы прервём наше рассмотрение замечанием онтологического характера. В отличие от случая с классической теорией множеств (в которой внешний мир является классом чётко разграниченных объектов, а мышление как процесс из неё выпадает), в р-адическом мире внешние объекты имеют ту же «геометрию», что и объекты психического свойства. Последние, таким образом, уже на формальном уровне становятся отражением (или частью?) внешнего мира. И мы вплотную подходим к архетипам сознания К. Г. Юнга и априорным категориям И.Канта.

Как теперь стало понятным, фракталы — это просто результат изменения аксиоматики, постулатов теории множеств. Но существует ли мир, строение которого можно принять в качестве аксиом? Знаком ли он людям? Оказывается, знаком и очень давно. Ответ мы находим в восточной философии. Восточная философия вообще в последние годы часто упоминается в связи с физикой, синергетикой и системными представлениями. Отмечено много поразительных аналогий между нею и новыми научными идеями[9][11]. Впервые параллели между физикой и восточными учениями были исследованы в знаменитой книге физика Ф.Капры «Дао Физики», вышедшей четвёртым изданием в 2000 году. Для полноты картины процитируем один из его главных выводов: «..."бутстрапная" философия не только отказывается от фундаментальных "кирпичиков" материи, но вообще не принимает фундаментальных сущностей — констант, законов или уравнений. Материальная Вселенная рассматривается как сеть взаимосвязанных событий Ни одно свойство какой-либо части этой сети не является фундаментальным: все свойства одной части вытекают из свойств других частей, и общая связанность взаимоотношений определяет структуру всей сети»[6]. Как видно, в изучаемом нами фрактальном мире эти аналогии обретают дальнейшее продолжение, но уже со стороны математики.

Поскольку понятия философии и математики сформированы в разных интеллектуальных сферах и детальное выявление параллелей — тема самостоятельной работы (см., например,[11][12]), то здесь мы ограничимся перечислением лишь наиболее очевидных аналогий, и изложение будет в основном опираться на статьи географа А.Д.Арманда, востоковеда Т.П.Григорьевой, на монографии востоковеда А.И.Кобзева, философа Е.Н.Князевой и математика С.П.Курдюмова.

I. Фрактальное, р-адическое пространство-время, имитируемое соленоидом, структурно есть иерархия вложенных циклов и поэтому вполне допускает наличие таких атрибутов мира, как «Дыхание Брахмы», ритмы инь-ян, то есть циклическую смену периодов свёртывания и развёртывания Вселенной. В таком замкнутом мире формой закона сохранения энергии можно считать закон Кармы, согласно которому за каждое своё действие с неотвратимостью мы получаем наказание или поощрение в строгом соответствии с размерами совершённых вреда или пользы[8]

Объединение языка и физики в р-адической математике можно трактовать как то, что р-адический фрактальный мир представляет собой Единое — Духоматерию. Связь Духа и Материи в этом единстве аналогична принципу дополнительности Н.Бора, который сделал символ инь- ян своей эмблемой.

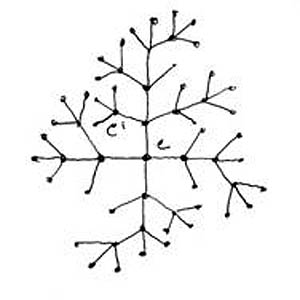
Рис.5. Дерево Брюа-Титса (Р=3)

Теперь о семёрке. Правило «7±2» хорошо известно в психологии и во многих других системных науках. В р-адической математике простое число р=2 занимает особое положение. Ему соответствует Канторово триадное множество. Специалистам- топологам известно, что оно совершенно исключительно по своим свойствам в классе самоподобных множеств. Существует точно девять полностью или равномерно самоподобных множеств (экспоненциально полных)¹⁰; первые два — патологичны («пустое» и состоящее из одной изолированной точки); остальные семь получаются простыми операциями композиции из Канторова триадного множества. Явление нетривиального самоподобия имеет точно семь компонентов, которые определяют структурное различие между типами объектов, «населяющих» мир. Тогда процессы, в которых участвуют такие объекты, сохраняют фрактальную структуру мира (точнее, 2-адическую, бинарную или дихотомическую).

II. «Срединный Путь» в науке состоит в том, что «наука перестаёт быть антропоморфной, противопоставляющей человека остальному миру»[9]. Во фрактальном мире, как уже говорилось, сходятся язык и физика, едиными становятся человек и окружающая среда.

«Точка есть сжатая Вселенная», «бесконечное в конечном», «Восток не знает анализа»[9] — эти представления в нашем изложении значат, что любой, сколь угодно малый кластер фрактального, плохообусловленного мира есть микрокосм, сохраняющий исходную р-адическую структуру, поэтому он бесконечно сложен и мироподобен.

«Мир полицентричен», «мир напоминает бескрайнюю сеть Изиды, украшенную драгоценными камнями и кусочками хрусталя, <...> каждая драгоценность отражает все остальные»[9] — эти идеи просматриваются в дереве Брюа-Титса, в р-адической сети кластеров-микрокосмов, в их взаимопроникновении.

«Теория познания неотделима от переживания» — гласит учение Востока[9]. Соответственно, так как р-адическая сеть строго объединяет объекты и их связи, то невозможно произвольное введение наблюдателя или какой-либо другой причины извне мира. Наблюдатель должен быть частью мира и переживать изменения вместе с ним¹¹. Движения и процессы в подобном мире носят характер лишь самоорганизации или синергии[11]. Такое положение наблюдателя отвечает закону ЕСТЕСТВЕННОСТИ.

«Истина вне слов»[9] — это ещё одна, малознакомая, форма широко известного логического «парадокса лжеца». Как отмечалось выше, плохообусловленный мир даёт права на существование логических парадоксов в силу присущей ему глубины. Поэтому любой конечный текст всегда остаётся лишь приближением к Истине. Математически этот факт соответствует недавно доказанному свойству неразрешимости фрактальных множеств. Проще говоря, истинному р-адическому числу присуща бесконечность, в то время как любое слово, любой текст всегда конечны по форме.

«Одно рождает два, два рождает три, три рождает всё остальное»[9] — этот философский тезис трактует организацию мира из первооснов. Здесь двойка снова занимает исключительное положение. Приведённый выше 2-адический соленоид можно получить, «измерив» натуральный ряд чисел р-адическим образом, то есть степенями двойки (октавами! — Ред.). Легко видеть, что получим так называемый «порядок Шарковского», известный из теории хаоса. Этот порядок формируют степени двойки и его можно рассматривать как иерархическую структуру 2-адического соленоида, где тройки «открывают» линейную последовательность чисел на каждом уровне иерархии. Именно двойка ставит в специфическое положение тройку в конструкции мира. Поэтому теорема «порядок три рождает хаос» приобретает некоторое общее звучание. Ведь согласно космогониям всех народов[12], Хаос есть первоначало всех вещей.

III. В китайской натурфилософии геометрические и числовые построения образуют неразрывное единство[10]. Очевидно и р-адические числа могут служить примером пространственно-числовой системы. Рассмотренные выше свойства чисел также вполне соответствуют отсутствию доминирования на Востоке представлений об атомизме и дискретности как пределе деления. Для китайцев характерно разграничение не индивидов и множеств, а множеств и подмножеств. Именно поэтому в китайской философии вопрос о существовании иррациональных чисел не стоит — ведь нет предела делимости материи. Этому соответствует конструкция плохообусловленных множеств и полей р-адических чисел.

Создаётся впечатление, что фрактальный мир и есть та своего рода «прасреда», связывающая все объекты и явления[11], а р-адическая математика намечает, пусть формально, прорыв в инобытие, «дающий возможность понять Природу, исходя из неё самой, законов Бытия, а не наших представлений о нём». Человек есть вещь среди вещей, часть природы и должен следовать закону ЕСТЕСТВЕННОСТИ. Или, по словам Тейяр де Шардена, «истинная физика та, которая сумеет включить всестороннего человека в цельное представление о мире». Не случайно анализ многовековых исканий человечеством законов социального устройства приводит философа В.В.Василькову[12] к выводу, в котором слышатся основные моменты нашего изложения: «Структурно-эволюционным основанием социального упорядочения выступает единая для всех народов универсальная мифологическая модель космообразования... Такой порядок, согласно мифологическим представлениям, выстраивается по законам универсального подобия. Используя современные аналогии, можно сказать, что мировой порядок разворачивается, структурируется подобно глобальному фракталу, воспроизводя в каждом участке (фрагменте) картины мира, первоначальный структурный рисунок, описанный в мифах как образование Космоса из Хаоса».

Примечание

¹ Публикацию о фракталах можно найти в № 11(3/1997): Ф.А.Цицин «Фрактальная Вселенная».

² Под термином множество в математике понимается совокупность по ряду признаков однородных элементов; fractio (лат.) — доля, часть.

³ Фрактальная размерность интуитивно может быть понята как степень заполнения пространства нерегулярно распределённой субстанцией. Топологическая размерность — это хорошо известные из элементарной геометрии числа степеней свободы, присущие точке при движении (по линии — 1, по поверхности — 2, в пространстве — 3).

⁴ О свойствах р-адических чисел смотрите далее. Напомним, что действительными числами называются числа целые, дробные (рациональные и иррациональные),положительные и отрицательные.

⁵ Комплексные числа включают в себя, помимо действительных, мнимые числа (мнимая единица i = √-1 ). — Прим. ред.

⁶ Простые числа делятся лишь на единицу и самих себя. — Прим. ред.

⁷ Кластерная структура — картина строения объекта в виде скоплений элементов, расстояние между которыми меньше расстояний между их скоплениями. При «близоруком» взгляде кластер видится целостным объектом.

⁸ Это напоминает эффект, теоретически описываемый как расширение пространства Вселенной из начальной сингулярности. — Прим. ред.

⁹ Во Вселенной на её максимально наблюдаемых ныне масштабах фиксируется сетчатая структура скоплений и сверхскоплений галактик, подразумевающая фрактальные её свойства. Прим. ред.

¹⁰ Такие множества пространственно однородны. В них нет больших «дырок», как в приведённых выше рисунках фракталов. Любые их подмножества в произвольных комбинациях, взятые в любом месте, сохраняют структуру и однородность исходного множества.

¹¹ Эта мысль по существу сродни знаменитому антропному принципу. — Прим. ред.

Список литературы

[1] W.Beyer et.al. S. Ulam: Sets, Numbers and Universes. MIT Press, 1974.

[2] Robert A. Eucledean Models of p-Adic Spaces. In W.Schikhoff et.al. p-Adic Functional Analysis. Nijmegen, 1995.

[3] Barwise J., Moss L. Hypersets. Mathematical Intelligencer, v,13(4), 1991.

[4] Владимиров B.C., Волович И.В., Зеленое Е.И. Р-адический анализ и математическая физика. М., Наука, 1994.

[5] Merzenich W., Stiger L. Fractals, Dimension and Formal Languages. In G. Rosenberg, A.Salomaa Developmets in Language Theory. World Scientific Publ. Co., 1994.

[6] Capra F. The Web of Life. Flamingo, 1997.

[7] Брушлинский A.B. Мышление и прогнозирование. M.: Мысль, 1979.

[8] Арманд А.Д. Время в учениях Востока. «Дельфис» №№ 14(1/1998), 15(2/1998).

[9] Григорьева Т.П. Синергетика и Восток. Вопросы философии, № 3, 1997.

[10] Кобзев А.И. Учение о символах и числах в китайской классической философии. Ин-т философии РАН, 1994.

[11] Князева Е.Н., Курдюмов С. П. Законы эволюции и самоорганизации сложных систем. М.: Наука, 1994.

[12] Василькова В.В. Порядок и Хаос в развитии социальных систем// Синергетика и теория социальной самоорганизации. СПб.: Лань, 1999.

"Дельфис" №23(3/2000)