Геометрия – это вам не физика,
где можно химичить.
Студенческий фольклор.

Понятийные особенности.

Понятие геометрической пропорции восходит к античной математике [1, ч. 7, гл. 6, § 1] и для величин c > b > a подразумевает равенство отношений c : b = (c – b) : (b – a) или с учетом свойств пропорции c : b = b : a. С данным равенством непосредственно связано среднее геометрическое двух чисел c и a – это такое третье число b, квадрат которого равен произведению исходных чисел. То есть среднее геометрическое двух чисел равно квадратному корню из произведения этих чисел. Так формируется полная терминологическая сопоставимость и преемственность.

Если ввести дополнительное условие c = a + b, то из геометрической пропорции образуется её частный случай – золотая пропорция (a + b) : b = b : a.

Иногда золотую пропорцию называют гармонической, что терминологически неправильно [2]. Ещё древние греки (Никомах, Папп, Архит) учили, что три числа образуют гармоническую пропорцию, если отношение двух из них равно отношению разностей между каждым из них и третьим числом: c : a = (c – b) : (b – a).

Отсюда непосредственно следует такое современное понятие как среднее гармоническое – это обратная величина среднего арифметического обратных величин

b^–1 = (a^–1 + c^–1)/2 → b = 2ac / (a + c).

Так, применительно к делению единичного целого 1 = b + a, гармоническая пропорция сводится к квадратному уравнению a² + 2a – 1 = 0 и дает решение: a = √2 – 1, b = 2 – √2.

Поэтому, если мы и хотим как-то подчеркнуть особую гармонию, присущую золотой пропорции, то, по крайней мере, её следует называть гармоничной, но не гармонической.

Анализ геометрических пропорций Ф. Германа.

Современные электронные коммуникации позволяют быстро знакомиться с новинками науки и технологий, отслеживать последние результаты исследований и что называется "по горячим следам" обмениваться мнениями.

Так, в своей недавней статье [3] педагог-математик Франц Герман порадовал читателей «планарными пропорциями», которые он связывает с делением единичного квадрата. Работа в целом нам понравилась. Особенно в её устремленности к поиску новых подходов и решений в области пропорций.

Вместе с тем, на наш взгляд, она содержит отдельные неточности, а также чрезмерное нагромождение необязательных преобразований, на что хотим обратить внимание и высказать некоторые собственные соображения.

1. Так, автор отмечает, что «понятие "золотая пропорция" связано с делением единичного отрезка на части...». В некоторой степени это верно. Хотя данное понятие намного шире и соотносится с пропорциональными зависимостями в разных областях знаний независимо от природы исходных параметров. Будь-то километры, килограммы, градусы, объемы тел и т.д. Ещё «в IV веке до н.э. древнегреческий математик Евдокс дал определение пропорции, составленной из величин любой природы» [4, с. 261].

Часто золотую пропорцию представляют в виде деления целого на две части, что методологически также неправильно. Вполне допустимо рассматривать пропорцию соразмерных величин вне понятия "целого". Например, сравнивать геометрические параметры двух объектов, расположенных в разных странах, и так далее.

2. Вводится некорректный термин "алгебраические пропорции", противопоставляя их делению единичного квадрата 1×1. – Так или иначе, практически все математические пропорции [2] разрешаются алгебраическими методами. Собственно говоря, и сам автор, пытаясь как-то отделить "алгебраические пропорции" от "планарных", свой анализ осуществляет с помощью решения систем алгебраических уравнений. То есть, де-факто нет особого различия, кроме необязательных терминологических наслоений и путаницы.

3. Выполняются красивые и наглядные геометрические построения с точки зрения золотой пропорции в единицах площади. Хотя многое здесь достаточно хорошо известно и сводится к построению прямоугольного треугольника Кеплера со сторонами (ф, √ф, 1). Последние дополняются квадратами, площади которых (ф², ф, 1) соотносятся в золотой пропорции, ф = (√5 – 1)/2 ≈ 0,618 – малая константа золотого сечения.

При этом стороны полученных трех квадратов он ошибочно называет пифагоровой тройкой. В действительности они таковыми не являются, поскольку пифагоровы тройки – это упорядоченный набор из трех натуральных (!) чисел, которые удовлетворяют квадратному уравнению x² + y² = z².

4. Далее автор переходит к ортогональному сечению квадрата 1×1 на четыре части двумя прямыми линиями: горизонтальной и вертикальной S₁ + S₂ + S₃ + S₄ = S = 1.

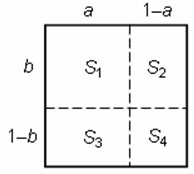
Составляет пары геометрических пропорций (с равными средними членами)

1 / S_r = S_r / S_t, 1 / S_u = S_u / S_v.

Затем производит вычисления и соответствующий анализ, перебирая двенадцать разных вариантов в порядке сочетания (следования) четырех числовых индексов r – t, u – v или в цифровом виде (r t, u v), со сменой величин площадей в записи пропорций по горизонтали, вертикали или диагонали.

Выполненная работа, безусловно, самоотверженная, но одновременно утомительная.

Решение задачи можно существенно упростить, обратив внимание на то, группа симметрии квадрата имеет восьмой порядок и включает все движения-преобразования, отображающие квадрат на себя: осевая симметрия с четырьмя осями (две по диагоналям и две через центры противолежащих сторон), а также центральная симметрия с четырьмя поворотами вокруг центра на 90⁰.

Поэтому достаточно рассмотреть лишь один вариант: горизонтальный однонаправленный (r t, u v) = (1 2, 3 4) или диагональный (r t, u v) = (1 4, 3 2).

Горизонтальный разнонаправленный или круговой вариант (r t, u v) = (1 2, 4 3) решений не имеет, ибо из пропорций следует S₁>S₂ или a > a – 1 и одновременно S₄>S₃ или a < a – 1, что невозможно.

К слову, рассматривая данный случай (движение в противоположных направлениях в разных вариациях), автор приходит к уравнению четвертой степени a⁴ – 2a³ – 2a² + 3a – 1 = 0 и пишет, что «точного значения решений данного уравнения вычислить не удается».

На самом деле точные значения четырех корней существуют a = [1 ± √(7 ± 2√13)] / 2. Однако все они действительно не подходят, ибо два из них мнимые, третий отрицательный, а четвертый больше единицы, что противоречит исходному условию a, b ≤ 1.

В случае (r t, u v) = (1 2, 3 4) имеем две пропорции 1/S₁ = S₁/S₂ и 1/S₃ = S₃/S₄. При этом S₁/S₂ = a / (1 – a) = S₃/S₄, следовательно, 1/S₁ = 1/S₃ или S₁ = S₃, откуда следует b = 1 – b или b = 0,5. Подставляя значение b = 0,5 в равенство S₁² = S₂ первой пропорции, получаем квадратное уравнение a² + 2a – 2 = 0 с положительным решением a = √3 – 1.

Остальные варианты пропорций равнозначны: либо значения величин a, b меняются местами, либо решение √3 – 1 дополняется своим симметричным аналогом относительно горизонтальной или вертикальной осей симметрии 1 – (√3 – 1) = 2 – √3.

Таким образом, учитывая осевую и центральную симметрии, для величин a и b фактически имеем одно решение: 0,5 и 2 – √3 = tg15⁰ = tg π/12 ≈ 0,268.

Однонаправленный порядок следования величин площадей, включая их "диагональные" движения в записи пропорций, слева или справа дает значение b = 0,5 (горизонтальная ось симметрии), а сверху или снизу – a = 0,5 (вертикальная ось симметрии).

Собственно и всё решение.

Говорить о какой-либо теории планарных пропорций пока также не приходится...

Об одном "квадратичном" свойстве рекуррентных последовательностей.

Ф. Герман приводит [3] любопытное свойство чисел Фибоначчи, однако, с чрезмерно усложненным доказательством. Между тем, описанная им закономерность имеет несложное обоснование. Более того, она характерна для широкого класса линейных рекуррентно-аддитивных моделей.

Напомним, в математике [5, гл. 5; 2–4] формула вида x_m+n = a₁x_m+n–1 + a₂x_m+n–2 + ... + a_mx_n называется линейным однородным разностным (возвратным) уравнением m-го порядка с постоянными коэффициентами a_j, m – числа натурального ряда.

При заданных начальных условиях X₀ = (x₀, x₁, … x_m) данное уравнение определяет линейную рекуррентную (возвратную) последовательность: начиная с исходной точки n = 0, каждый ее элемент x_m+n вычисляется через m предшествующих.

Выражение P(x) = x^m – a₁x^m–1 – a₂x^m–2 –…– a_m является характеристическим полиномом исходного разностного уравнения.

Согласно теореме Бернулли [6], если λ – единственный наибольший по модулю корень уравнения P(x) = 0, то для практически любого набора начальных данных линейная возвратная последовательность при n →∞ обладает свойством: lim x_n+1/x_n = λ.

В частности, для m = 2, a₁ = a₂ = 1, (x₀, x₁) = (0, 1) образуются числа Фибоначчи, Отношение соседних чисел стремится к золотой константе Ф = (1+√5)/2 – максимальному по модулю корню квадратного уравнения x² – x – 1 = 0.

Теперь перейдем непосредственно к обоснованию одного замечательного свойства.

Примем в качестве начальных условий X₀ целые неотрицательные числа, не равные одновременно нулю. Коэффициенты a_j – тоже целые (включая 0 и отрицательные значения), но с единственным условием: по мере увеличения индекса n обеспечить рост чисел x_n.

Тогда, начиная с некоторого номера, элементы возрастающей последовательности x_n – числа натурального ряда.

Сумма натуральных чисел, заключенных между двумя соседними элементами x_n и x_n+1, равняется полусумме первого и последнего чисел, умноженной на их количество:

S_n = (x_n + 1 + x_n+1 –1)·(x_n+1 – x_n – 1) / 2 = (x_n+1 + x_n)·(x_n+1 – x_n – 1) / 2.

Пусть n → ∞. Тогда разность x_n+1 – x_n несоизмеримо больше единицы, и сумма S_n становится равной половине разности квадратов S_n = (x_n+1² – x_n ²) / 2.

При этом отношения x_n+1 / x_n и x_n / x_n–1 неразличимы с точностью до бесконечно малой величины и согласно теореме Бернулли равны максимальному по модулю корню λ алгебраического характеристического уравнения.

Определим отношение сумм:

μ_n = S_n / S_n–1 = (x_n+1² – x_n²) / (x_n² – x_n–1²) = [(x_n+1 / x_n)² – 1] / [1 – (x_n / x_n–1)^–2] =
(x_n+1 / x_n)² = λ².

Итак, отношение смежных величин рекуррентного ряда стремится к корню λ, а отношение сумм натуральных чисел, заключенных между двумя соседними элементами, стремится к λ². Например, для чисел Фибоначчи предельное отношение сумм μ_n равно Ф².

Последовательность сумм {S_n} для чисел Фибоначчи, в частности, представлена в энциклопедии целочисленных последовательностей (Нил Слоун, http://oeis.org/A109454).

Ещё один анализ.

Продолжая разбор терминологических наслоений, уместно также упомянуть другую работу Франца [7]. Представленная в ней красивая и наглядная графика, к сожалению, перебивается необязательным введением новых терминов в области теории чисел.

Так, автор вводит термин «производная числа» ∂n от числа n – сумма всех делителей числа n, которые меньше n. Хотя в математике давно прижился термин "аликвотная сумма", равная s(n) = σ(n) − n, где σ(n) – сигма-функция или суммирующая функция делителей.

Вводит некое название "цепочки производных чисел", в то время как это известная аликвотная последовательность [8] – рекурсивный ряд, в котором каждый член является суммой собственных делителей предыдущего члена, то есть s₀ = n, s_k = σ(s_k–1) − s_k–1.

Каждое натуральное число на числовой оси автор дополняет по вертикали аликвотной последовательностью и в зависимости от величины s(n) разделяет числа на собственные и несобственные. Звучит не очень убедительно, ибо в теории чисел всё давно определено:

• недостаточные (deficient) числа s(n) < n – A005100;
• совершенные (perfect) числа s(n) = n – A000396;
• избыточные (abundant) числа s(n) > n – A005101.

Если автор что-то и выигрывает, то исключительно одну клеточку в отдельных местах, что на фоне «изучения Вселенной чисел» не имеет принципиального значения.

Аликвотные последовательности чаще всего бывают конечными или бесконечными с повторяющимся периодом.

Существуют также числа, для которых на сегодня не известно, являются ли их аликвотные последовательности конечными или периодическими: 276, 306, 396, 552, 564, 660, 696, 780, 828, 888, 966, 996, 1074, 1086, 1098, 1104, 1134, 1218, 1302, 1314, 1320, 1338, 1350, 1356, 1392, 1398, 1410, 1464, 1476, 1488, ... А131884.

Одним из подобных чисел, с которыми столкнулся Франц, стало число 138.

Действительно, судьба этого числа долгое время была неизвестной. Однако американский математик Д. Леммер (1867–1938) всё-таки установил, причем без компьютера (!), что начинающаяся с 138 аликвотная последовательность достигает величины 179931895322 после 117 шагов, а затем заканчивается единицей с общим количеством 177 шагов-итераций.

Любопытно, что среди чисел А131884 (условно говоря, с неустановленной судьбой) нет числа 138, зато наличествуют числа, кратные ему, в частности: 138·2 = 276, 138·4 = 552, 138·6 = 828, 138·8 = 1104.

Золотое окно.

В заключение предложим собственную простую интерпретацию золотого сечения, связанного с квадратами.

Геометрическая пропорция c / b = b / a, дополненная аддитивным соотношением c = a + b, дает золотую пропорцию x = (a + b) / b = b / a = a / (b – a) = Ф или b² – a² = ab.

Как видно, разность двух квадратов со сторонами b и a равна прямоугольнику a×b. То есть квадраты двух чисел уравновешиваются их произведением.

Так мы приходим к картинке, которую назовем "золотым окном".

Другими словами, из квадрата b×b вырезается квадрат a×a так, чтобы оставшаяся часть равнялась a×b.

Говоря языком художника, на голубом квадратном холсте b×b рисуется желтый «золотой квадрат» a×a. При этом площадь свободного поля равна разности этих квадратов.

Рассмотрим другие возможные варианты с разностью квадратов:

b² – a² = b / a, решения в области положительных чисел нет;

b² – a² = b – a, b + a = 1, множество решений;

b² – a² = b + a, b – a = 1, множество решений.

Таким образом, золотая пропорция – исключительное решение, способное единственным образом уравновесить два квадрата относительно простых арифметических операций с числами: сложения и вычитания, умножения и деления. Другими словами, квадраты двух неравных чисел можно уравновесить только их произведением. Либо третьим квадратом по теореме Пифагора.

Учитывая алгебраическую форму разности квадратов b² – a² = (b – a)·(b + a), получаем, что в золотой модели произведение суммы и разности положительных чисел равно их произведению.

Литература:

1. Лосев А.Ф. История античной эстетики / Т. 8. Итоги тысячелетнего развития. Книга 2. – М.: Фолио; АСТ, 2000. – 688 с. – URL: http://psylib.org.ua/books/lose008/index.htm.
2. Василенко С.Л. Средние значения и математические пропорции: от Античности до наших дней // АТ. – М.: Эл. № 77-6567, публ. 22763, 28.11.2016. – URL: trinitas.ru/rus/doc/0016/001e/00163146.htm.
3. Франц Герман. Теория планарных пропорций // АТ. – М.: Эл. № 77-6567, публ.24945, 18.11.2018. – URL: trinitas.ru/rus/doc/0016/001g/00163845.htm.
4. Савин А.П. Энциклопедический словарь юного математика. 2-е изд, испр. и доп. – М.: Педагогика, 1989. – 352 с.
5. Гельфонд А.О. Исчисление конечных разностей: Учеб. пособие. – 4-е изд., стер. – М.: КомКнига, 2006. – 376 с.
6. Василенко С.Л. Гармоническая пропорция в линейных разностных уравнениях // АТ. – М.: Эл. № 77-6567, публ.15330, 09.06.2009. – URL: trinitas.ru/rus/doc/0232/009a/02321111.htm.
7. Франц Герман. Вселенная чисел // АТ. – М.: Эл. № 77-6567, публ.24229, 30.01.2018. – URL: trinitas.ru/rus/doc/0016/001f/00163603.htm.
8. https://ru.wikipedia.org/wiki/Аликвотная_последовательность.