В статье описываются результаты теоретических исследований по распространению заузленной электромагнитной волны.

Цель теоретического исследования состоит в том, чтобы, используя топологические свойства расслоения Хопфа сферы S² в сферу S³ [1], вычислить в явном виде функцию, которая описывает движение импульса заузленной электромагнитной волны (ЭМВ) в форме торического узла в стереографической проекции поля (в виде электромагнитного солитона) из S³ локально на трёхмерное евклидово пространство R³. Эти исследования необходимы для создания технических передающих и приёмных антенн, существующих именно в пространстве R³.

Теоретический аспект существования заузленного электромагнитного поля состоит новых нетривиальных топологических решениях уравнений Максвелла, записанных во-вторых внешних дифференциальных формах. Именно существование электромагнитного поля, описываемого этими уравнениями, обусловлено явлением расслоения Хопфа [1] в гиперсферу S³ физического пространства (вакуума), где стереографическая проекция параллелей S³ в каждой её точке на наше наблюдаемое 3-мерное евклидово пространство имеет форму заузленных 3-х мерных торов. Линии меридианов (окружностей Вилларсо) этих торов задают орбиты группы U(1) внутренней симметрии электромагнитного поля (т.е. слои главного расслоения). Эти линии в физических размерностях и определяют силовые линии магнитного и ортогонального электрического поля, а связность этого главного расслоения определяет напряжённость физических полей. По сути, эти заузленные торы (или узлы торического многолистника) силовых линий электромагнитного поля и являются указанным выше топологическим решение уравнений Максвелла.

Для того, чтобы вычислить в явном виде функцию, которая описывает движение импульса заузленной электромагнитной волны (ЭМВ), расслоение Хопфа 2-мерной сферы S² в 3-х мерную сферу (гиперсферу) S³ рассматривается в 4-хмерном евклидовом пространстве-времени R⁴ с картой (координатами)

h=(ϕ, θ)= (ϕ(x₁, x₂, x₃. x₄= с•t), θ(x₁, x₂, x₃, x₄= с•t)) S³→ S² ,

где с - скорость света, t – время; ϕ, θ - комплексные ортогональные скалярные функции.

В этом 4-мерном евклидовом пространстве уравнение сферы

S³ : x₁²+ x₂²+ x₃²+ x₄²=1,

а (стерео)проективное 3-х мерное пространство R³={y₁, y₂, y₃},

где y_i= x_i /(1- x₄), где x₄ - ось времени с•t в R⁴.

Обратное преобразование в R⁴ из R³ равно x_i= 2y_i /(ρ + 1), x₄= (ρ ‒1) /( ρ + 1), ρ=∑ y_i^2.. Комплексная плоскость скаляров (φ, θ) отображается этой картой Хопфа в сферу S² и другой стереографической проекцией в комплексную плоскость С: S²=R² U{∞}= С U{∞}.

В результате таких двух компактификаций комплексные скаляры ϕ и θ могут быть интерпретированы, в любой момент время, как отображение карт Хопфа S³→ S², которые могут быть классифицированы в гомотопических классах, охарактеризованных значением индекса Хопфа n. Это расслоение Хопфа глобальное. Линии уровня скаляров по построению совпадают с магнитными и электрическими силовыми линиями (в физической размерности), каждая из этих линий помечена постоянной величиной соответствующего скаляра ϕ= ϕ₀ , θ= θ₀. Оба скаляра принимают одно и тоже значение на бесконечности, которое эквивалентно компактификации (замыканию) физического 3-пространства R³U{∞} в сферу S³.

Рассматриваются электромагнитные волны, для которых справедливо скалярное равенство B•E =0, где B=μ•H - вектор магнитной индукции, μ=1 - магнитная проницаемость вакуума, E- вектор напряжённости электрического поля.

Скалярное равенство B•E нулю означает ортогональность векторов B и E, а значит ортогональность (дуальность) их линий уровня. При этом по построению линия уровня скалярного поля ϕ касательна вектор-фунции B(ϕ), а линия уровня скалярного поля θ касательна вектору E(θ) для начального момента времени t=0 (аналитическое вычисление этих векторов описано ниже). Таким образом, имеем следующие выражения для векторов:
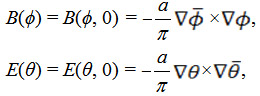       (1)

где величина a используется для получения правильных размерностей физических величин индукции магнитного поля B и напряжённости электрического поля E. Точкам на сфере S² Римана или Блоха, или гомологической сфере Пуанкаре соответствуют в гиперсфере S³ после стереографической проекции на R³ замкнутые в окружности Вилларсо линии уровня в виде зацепленных силовых линий (для кручёной ЭМВ), образующие геодезические меридианы 2-х мерного тора слоя в S³ , а самозацепленные силовые линии образуют заузленный тор в виде торических трилистников, пятилистников, … , многолистников заузленной ЭМВ. Свойство геометрических линий уровня определять именно силовые линии электромагнитного поле (с точностью до физических размерностей векторов касательных к ним) обусловлено тем важным фактом, что поскольку внешний дифференциал от 2-форм элемента поверхности S² равен нулю, т.е.

dω_ϕ=0, dω_θ=0, (2)

то эти формы замкнуты [2]. Локальное расслоение Хопфа F*: S³→ S² по сути становится для внешних форм операцией оттягивания (“pullback”) или в российской нотации – перенесения 2-формы элемента поверхности S² и внешнего дифференциала от формы в гиперсферу S³.

формате PDF (230Кб)

1. A. F. Ranada, J. L. Trueba Topological electromagnetism with hidden nonlinearity. Сборник: Modern nonlinear optics Part 3. Second Edition Advances in chemical physics. Volume 119. 2001 John Wiley & Sons, Inc. ISBNs: 0-471-38932-3 (Hardback); 0-471-23149-5 (Electronic), р 197.

2. A.F.Ranada. Knotted solutions of the Maxwell equation in vacuum. Journal of Physics A 23, I.815-L.820, 1990.

опубликовано в журнале "Успехи современной радиоэлектроники", 2017, №5, с.45