|
|
|
Никитин А.В.
Оглавление
Время собирать
Эталон, это – Я
Долой эталон
Но, проблема … осталась
Сложности понимания
Идеи и модели
И снова поиски
Блуждание в логиках.
Что есть логика?
Нечеткая логика
Логическая система…на случайностях
Локализация случайностей
Наложение случайностей
Перед выбором
Случайность в действии
Основы логики
Единицы системы.
Математика конкретных образов
Для чего все это?
Подведем итоги
Литература
Нет, напрасно мы решили.
Прокатить кота в машине.
Кот кататься не привык.
Опрокинул грузовик.
Агния Барто.
Время собирать…
Зачем так уж необходимо знать, как мы думали когда-то, как думает весь живой мир нашей планеты, если мы давно уже думаем совсем иначе?
Видимо надо понять, как мы стали такими, как прошли этот путь от клетки до себя, до нашего мозга, который вдруг понял что-то и стал работать чуть иначе. Чуть логичнее, чуть аналитичнее, чуть абстрактнее…
Эти «чуть» сделали человека. Но, человек находится на самом верху лестницы эволюции. А вот те, что ниже, они и есть настоящие создатели той логической машины, которая называется – мозг.
Мозг, это почти компьютер, подключенный к телу..., для контроля состояния и управления. Сложная, но - машина.
Хорошая машина, на уровне среднего телецентра и правительства среднего государства. Если бы они работали в автоматическом режиме. А под контролем - Земля, если оценивать по количеству клеток, как жителей этого государства. Всех надо кормить, лечить, защищать, следить за здоровьем, ... - это нормальные функции государственного управления...
Даже не одна машина, а комплекс из нескольких машин. И все охвачены мощными каналами связи. Сложная иерархическая многоуровневая система управления, с автоматическими каналами обмена данными, с огромными функциональными возможностями.
Вот это наш мозг. Так к нему и надо относиться.
С уважением и пониманием.
Видимо есть какие-то основополагающие принципы, которые объективно создали условия для формирования единого принципа формирования логического аппарата независимо от уровня развития того или иного живого существа.
Я давно размышляю на тему логических основ заложенных в основу формирования автономных логических систем, тех самых живых существ, что есть вокруг нас.
Понятно, что все началось с наложения случайностей. И неважно пока, из чего, на уровне клетки образовалась логическая схема, простейшая, но … работающая. На самом низком уровне. Замкнулась цепь обратной связи между ХОЧУ и МОГУ.
Система началась с действия. Достижения цели. Всеми возможными средствами. И даже невозможными.
Находить главное, отсеивая второстепенное. Пусть на уровне случайного, дважды случайного, трижды,… но однажды находить. Этот путь постепенно стал основным в логике Живого. Случайность стала обязательной составляющей логических решений и выбора. С поправками на ситуацию.
В клетке заработали механизмы логики. На самом низком, но, автоматическом уровне. На уровне 0 и 1. Там сформировались основы той логики, которая работает и в нашем мозге.
Мне всегда было интересно понять вот эту, автоматическую логику. Потому, что она определяет все остальные уровни развития. Там начало нашей логики. Нашего Я...
Если все это есть в реальности, то, как это применить в существующих условиях? В моих поисках это присутствует всегда. И потому понимаемая сложность реальности почти автоматически переходит в моделирование желаемого. В допустимое упрощение. В простые схемы для возможности применения прямо сейчас, на том уровне электроники, какой есть вокруг.
Да, по сути, и всё написанное мною, это те же попытки моделировать найденные мною крупицы знаний, как простейшие системы и задачи.
Знания добываются медленно, а желание применить найденное прямо сейчас, это присутствует всегда.
Круговерть калейдоскопа изложения разных, не связанных между собой тем, это лишь желание охватить суть проблемы со всех возможных сторон. Написано много разного, а порой и противоречивого.
Ну что же, пришло время хоть как-то систематизировать по разным кучкам то, что оказалось в этом большом клубке, называемом - Логика Автономных Систем или Логика Само...
Какой-то странный путь получился. С вершин Разума вглубь очевидных истин. К полному упрощению и деградации понятий. От сложного к простому. От Разума к Интеллекту, от Интеллекта к Автомату, от Автомата к … простейшим логическим действиям и понятиям. На тот уровень, где и ДНК – сложная логическая система. Вот где-то там и запрятаны основы нашей логики.
Но, оказывается, я только повторил уже пройденный путь. По нему шла наука. Это началось почти век назад.
Эталон, это – Я.
Начиналось всё, естественно, с Разума. А как же,…мы же такие умные…
Потом, постепенно, но приходит понимание, что Разум, это уж слишком… высоко. Он же имеется только у человека. А мы обо всех думаем.
Нет, пока – только Интеллект.
Но и тут сложности возникают, те же самые. Все стремятся охватить сразу всю проблему, целиком. И опять начинают с самого сложного – с себя. Почему я такой? Почему мы, …
И всё. На этом можно заканчивать. Тут написано столько, что жизни не хватит, чтобы прочитать все философские труды на эту тему.
То же самое происходит и с пониманием проблемы технического моделирования логической системы мозга.
Всё начинается и заканчивается … философией. Сравнением, оценкой, возможными вариантами последствий, но всегда … по отношению к человеку. Мы почему-то всегда нацелены на … себя.
С этого начиналось осмысление проблемы создания Искусственного Мозга в начале прошлого века. В этом причина неудачи с Логической Машиной. Цель ставилась недостижимая, даже в принципе. Но, понятная – Я.
Если Искусственный Мозг, то – Мое подобие.
Только так, а иначе, … зачем начинать?
Человек – венец Природы. Её лучшее творение. В нем собрано всё самое, самое... И если уж повторять, то вот этот Идеал. А на меньшее мы не согласны.
Кибернетика, возникшая на основе Логической Машины, сразу сменила вектор развития. Но, не Цель. Мы создадим Искусственный Мозг на основе машинной логики, надо только подождать…
Подождать. Развитие машинных методов обработки информации на основе математической логики, развитие математических методов решения логических задач, все это должно было привести к расцвету счетных машин.
И привело. Сложность исходной цели, наконец-то, была осознанна в полном объеме. А потому, не решаемая целиком, задача была разбита на технические составные части. По Декарту. Если нельзя всё и сразу, будем постепенно и по частям. Вполне закономерное решение.
Главной составной частью этой программы стал Искусственный Интеллект. Система логических правил развития. С нуля. С самого начала…
Не тут-то было…, техническая, в начале, задача сразу была приведена в состояние … философской проблемы.
И опять возник тот же эталон сравнения – Я.
Возможности симбиоза и конфликта Человека и Машины не обсуждал только ленивый. Изменился только технический уровень сравнения.
При таком подходе к проблеме Искусственный Интеллект был обречен…
И опять последовало то же решение. Проблема слишком сложна, надо решать её по частям. По степени сложности системы. Взаимодействие в колонии простейших автоматов - в одну кучку, возможное развитие обособленной программы – в другую, а глобальные системы управляемых взаимодействий – в третью. Последняя группа, как и предполагалось, только в порядке изучения проблемы.
Витиеватость и многополярность развития вычислительной техники, многообразие технических решений окончательно раздробили общую задачу на составные части. Теперь нейропроекты и элементы ИИ в программах, это уже разные вещи.
Проблема есть, а решения проблемы – нет.
Главная причина этого – эталон.
Долой эталон…
Это стало понятно не сегодня, и даже не вчера.
Зачем сравнивать заранее несравнимые величины? Найдем что-нибудь попроще. Интеллект, он же – разный. У бабочки один, у лягушки – другой, а у мышки – третий…, и интеллектов этих… много. А раз так, то задачу можно разложить на составляющие, по классам интеллекта.
Но можно и еще глубже копнуть. До нейронов. И до остальных клеток.
Копнули…
И запутались в бесконечных спорах. О свойствах и аналогах нейронов, о классификации интеллектов, о логике клетки. Потом все же определились несколько больших групп: За нейронные аналоги, против, примитивный ИИ, высокоразвитый, можно создать простейший интеллект электронными средствами, невозможно его создать на этом уровне техники…
Повоевали, … и все вместе ушли в программирование.
Причины. Их несколько. Но, главная – нет предмета спора. ИИ нет - никакого. До сих пор. Ни на какой основе. Различия подходов оказались непринципиальными - разными сторонами одного процесса. На том этапе – программирования. Цифровая техника другого пути и не оставила.
Интеллектуальные системы управления. Есть сегодня такие. Системы управления с использованием некоторых интеллектуальных приемов отбора и обработки информации. Техника развивается в эту сторону очень стремительно. И кажется, завтра мы снова заговорим и об Искусственном Интеллекте, и об Искусственном Разуме, и о Машинном Мозге…
Да, наверное …, но это будет уже другой разговор.
Похоже, что главный выбор в этом направлении уже сделан. Машине интеллект не нужен. Как бы она не улучшала свои возможности, она должна быть полностью управляемым объектом. Так это, по крайней мере, предполагается…
А вот элементы интеллекта в системе управления очень даже приветствуются. Для сближения оценок машины с нашими оценками и действиями. Для упрощения перевода и улучшения восприятия. Для интуитивного понимания своих действий оператором, принимающим решения. Сложность машины растворяется в элементах интеллекта, понятных оператору интуитивно, привычных с детства. Так и должно быть. Хороший слуга должен быть только тенью своего господина.
Но, проблема … осталась.
Она никуда и не исчезала. Ею почти перестала заниматься большая математическая наука. Этой проблемой занимается психиатрия, психология, но каждая решает свою задачу. Практическую. Занимаются вольные исследователи. Тут направлений … не перечтешь. И думается, найдут решение когда-нибудь.
Наконец-то, к изучению принципов деятельности мозга подключилась современная вычислительная техника и программирование. Возможно, уже скоро мы будем управлять машиной только силой мысли. Тут прогресс весьма ощутим. Значит, начали мы понимать, как работает наш мозг? Да, отчасти.
Что мы поняли за последнюю сотню лет в техническом аспекте? Известно внутреннее строение. Мозг состоит из нейронов, которые объединены в большие сети, содержащие сотни тысяч и миллионов нейронов. Принципы объединения примерно известны. Обмен информацией – импульсный. Известны ритмы мозга. Добавочная сложность – химическое управление, например, гормонами. Тут тоже немного разобрались. Обработка информации имеет параллельный характер. Известны зоны мозга, отвечающие за работу тех или иных систем организма и самого мозга.
Это очень много. И все же…
Мы не знаем технического определения мысли. Мы не знаем принципов логической системы. Мы не знаем логических единиц системы. Мы не знаем принципов и способов, как хранения информации, так и её извлечения. Нам неизвестна система кодирования информации. Мы не знаем, как формируются и как удерживаются логические связи между блоками информации. Нам совершенно неизвестны способы логической обработки информации на микроуровне, на уровне групп нейронов.
Так есть проблема, или – нет? Конечно, есть. И сложности – огромные.
Сложности понимания.
Они в нас самих, в наших знаниях, в стереотипах. Мы находимся под огромным давлением наших собственных знаний. Мы попали в плен нашей техники. Теперь уже развитие техники диктует направления развития наших знаний. И, конечно, деньги. Потраченные на достижение существующего уровня. Это и определяет принцип преемственности. Для техники это стало основным требованием. Для всей техники, и для вычислительной – в частности. Любые изменения должны носить постепенный характер. Через серию не очень больших изменений. От одного уровня, к другому.
Да, это техническая эволюция.
Эволюционный принцип развития выгоден во многих случаях. Он имеет массу достоинств. И потому, принят во всем мире, как основной. Он не отменяет открытий, но производит их отбор. По своим критериям. Прежде всего – эффективности. Что мы получим, если применим вот это новое? В чем мы выиграем? Если осязаемого эффекта нет, то зачем нам это открытие?
Вопросы совершенно справедливые и очевидные. Они диктуются эволюционным принципом развития. Кажется, иначе рассуждать мы уже и не умеем…
Но, пришлось же, поступаться эффективностью, когда наш прогресс привел нас к экологическим катастрофам. Оказывается, сиюминутная эффективность не всегда лучший вариант…
Оказывается, что эволюционный путь развития техники имеет и существенные недостатки. Он вынужден отбрасывать принципиально новые технические решения по требованиям преемственности, и тем … тормозит свое движение вперед.
Потому, что, даже самые перспективные технические идеи когда-то устаревают. Даже, в принципе. А все новые идеи уже отброшены и забыты. Но, развитие должно продолжаться. Надо, надо что-то … новое.
И тогда эти уже изрядно забытые идеи снова вынимают из небытия, оценивают, теперь уже в новых условиях, но опять, … со старым подходом. Начинается бесконечный компромисс между новыми идеями и уже привычными вариантами технического исполнения и применения. Когда такой компромисс невозможен, идея, даже самая блестящая – умирает. Теперь уже навсегда…
Эволюционный прогресс консервирует базовые принципы развития того или иного направления техники. Они необходимы для сохранения преемственности. Для вычислительной техники это: двоичная система счета, булева логика, система кодирования информации. Конечно, сегодняшний компьютер очень отличается от первых ЭВМ, но базовые принципы – неизменны.
Этот же принцип преемственности закреплен и в системе наших знаний. Радикальные преобразования тут имели место, но всегда были связаны с огромными трудностями преодоления сложившихся стереотипов. Мы привыкаем к определенному пониманию и радикально изменить наши взгляды на то или иное очень сложно.
Но приходится ломать устоявшееся, и уже устаревшее представление на новое…, куда ж деваться, если факты напирают. Меняем, но, с трудом, … и все время оглядываемся назад. Привычное живуче, новое не принимается сразу.
Вот так и живем, на перепутье. Направо – болота, налево – болота, вперед – страшновато, назад – неохота.
Идеи и модели …
Когда-то давно, может быть лет двадцать назад, мне вдруг представилось, что мозг, пока темный и непонятный объект, соединен с управляемыми им органами какими-то каналами связи. Каналов таких много, они ведут куда-то, образуя густую сеть с массой пересечений. И по этим каналам светящимися точками бегут импульсы. В разные стороны.
Вот же, что такое мозг – коммутатор. Он соединяет каналы связи, переключает их, формирует импульсы, направляет их куда нужно, и принимает … со всех сторон. И все это – нейроны. Универсальные ячейки огромной сети. Универсальные, одинаковые…, да и работают они все … одинаково. Из них состоит и логика, и каналы, и приемники, и передатчики импульсов. Из одинаковых узлов, как детский конструктор. Собрал в одном порядке – канал связи, собрал иначе – логическая схема. Еще раз иначе – получил генератор импульсов. Разобрал всё – и опять чистое поле, можно снова создавать из этих же элементов новый вариант логической системы. И всё всегда под рукой…
Кирпичики, из которых можно строить модели, разрушать, и снова строить. Пока не получится то, что нужно. Самый оптимальный вариант.
Из чего сегодня делаются логические схемы? Из электронных схем. Чтобы менять назначение этих схем надо менять назначение подводящих проводов. Вход, выход, обратная связь, …, нет, провода явно мешаются. Их в автоматическом режиме не перебросишь. Какие-то куски проволоки, а мешаются больше всего…
Так это же и есть … каналы связи. Те самые. По которым импульсы бегут…
Вот оно что …
Провода и надо заменять универсальными ячейками[31]. Да, электронными, да – сложными, но тогда не будет проблем с созданием новых связей.
Проводов-то … нет. Есть каналы связи, которые можно быстро собрать от одного пункта к другому, и так же быстро разобрать. И собрать в другом месте. Без проводов, жгутов, кабелей…
Ну, конечно, мозг – «черный ящик». Закрытый объем, самостоятельно формирующий связи, изменяющий их, каждый раз, под каждую новую задачу…
И мы туда забираться, чтобы поуправлять - не имеем права. И не должны. Потому, что в общем случае, он должен решать эти задачи оперативного изменения собственной структуры только самостоятельно. Как решит, так и будет.
Но, для этого мы должны заложить в него эти возможности.
Я не знаю, что такое наш мозг в реальности. Но, эта функция в него заложена. И если есть необходимость создания его модели, то начинать надо, …. в том числе и с этой функции. Возможности самостоятельной перестройки внутренней структуры. Не знаю как, но … надо. Значит, должна структура меняться … сама. Без постороннего вмешательства [31].
Сказка какая-то…
Ну, а если – нет? Если все же есть такие возможности?
В конце концов, я же просто моделирую возможность перестройки объема электронной логической схемы в динамическом режиме. Сложность пока значения не имеет. Мы просто проверяем такую возможность. Можно или – нет. В принципе. Теоретически.
Ну, если только теоретически, в принципе, то …
Электронная логическая схема работает с импульсами. Импульс … , а что такое импульс? Бросок напряжения. Счетный импульс, это логическая единичка, бегающая по схеме, что-то включает, выключает. Она, то - считывается, то -записывается, то - считается…, стоп…, число, количество…, надо поискать…
Количество, это единицы, находящиеся в пространстве. Эти единицы образуют объем счета. Они как-то взаимодействуют…
Вернулся к числу. Число, это …
Нет, не так. Позиционная система счисления предполагает установку единиц в числе по их статусу, в зависимости от того, что понимается под единицей, стоящей в том или ином разряде числа. Единицы, десятки, сотни…
Если все разряды числа уже полны, а мы все же добавим еще одну…
Происходит переполнение. Единицы этого разряда автоматически складываются в единицу следующего, старшего разряда … и уходят отсюда в тот разряд, как новая разрядная единица. Но и там все занято. Значит там возникнет тот же процесс … сложения и перехода в следующий…, понятно. Число преобразуется. Было 999, а добавили еще одну единичку, и стало … 1000. Это уже движение. Пока по числу в позиционном написании, но…
Если число очень длинное, то … это и не число уже, а цепь из разрядов [31]. А по ним бегут единички. И нам все равно, какой тут разряд, много это, или - мало. Всё равно. Есть цепочка разрядов, есть счетные единички, которые как-то там суммируются, перескакивают из одного разряда в другой, двигаются по этой разрядной цепи, которая когда-то была … числом. И приходят к концу этой цепи. Пришли, … а дальше хода нет. Тут и стоит … приемник этих единиц. Принял единицу, что-то отработал. И снова ждет. А на другом конце этой разрядной цепочки – генератор. Он генерирует единички и сбрасывает их в разрядную цепь. Одну за другой. Там генератор сбросил, тут приемник поймал…
Цепочка, вроде считает, передвигает единички, доводит их до приемника.
Так считает она или нет? Считает, и … двигает.
Вот он – канал связи. Число[31].
А есть ли такие системы счисления, в которых число все время готово к полному преобразованию, и оно происходит, но к стабилизации, как 1000, число не приближается? И число все время находится в состоянии готовности.
Посмотрел и покрутил несколько систем счисления [31]:
Единичная система счисления
Система Бергмана
Коды Фибоначчи
Двоичная система счсления
Система А.П.Стахова (квадраты четных степеней Ф)
Квадраты нечетных степеней Ф
Есть. Это система Бергмана, с основанием Ф. Нормальное состояние числа: 10101010…
Очень подходящий вариант. Емкость разряда мала, значит, движение единиц будет достаточно быстрым. Но, импульс, это все же – единица. А не её кусочек, часть…
Есть система без дробных чисел с такими же свойствами. Коды Фибоначчи [31]. Тут все только в единицах. Но, первый разряд какой-то непонятный. Он должен быть, похоже, сразу двухразрядным. И как 1 и как 10…
Где тут что? Куда подавать единицы с генератора?
А мы разряд построим и посмотрим. Так как он есть – двухразрядный. И уберем лишнее.
Не убирается.
Тогда разнесем разряды подальше и будем экспериментировать.
Вот как. Только при треугольной структуре разрядов число в системе кодов Фибоначчи начинает работать, как положено. Передавать единицы в следующие разряды.
Вернемся к системе Бергмана. Тут, оказывается, то же самое. Работает.
И даже больше, единички теперь бегут не в одну сторону, а в две [31]. Поразительно. В обе стороны от точки генерации разбегаются счетные единицы. В сторону увеличения числа, как и задумывалось. И в сторону его … дробной части.
Есть двухсторонняя передача импульсов в канале связи. Мы же помним, что нам не число нужно было, а канал связи на его базе. Число, это только модель.
Да, модель. Для технической реализации. Это же электронный счетчик бесконечной длины. То, с чего когда-то начинались ЭВМ. Триггеры со счетным входом, согласующие обратные связи, шины управления…, классика цифровой техники. Вот такой счетчик и можно использовать, как канал передачи информации.
Счетчик вместо … провода. Дорого? Это, как сказать. Когда-то мы не понимали, почему в японских транзисторных радиоприемниках количество применяемых транзисторов измерялось десятками, когда у нас - единицами. Вместо резистора - транзистор, это же дорого…, так мы тогда думали. Оказалось, плохо думали. Так что, давайте не торопиться с выводами…
Технический подход к каналу передачи на базе электронного счетчика позволил усмотреть новые проблемы. И новые возможности.
Да, можно собирать линию передачи импульсов из стандартных элементов. Да, возможно встраивать эти линии в общую схему логики, которая состоит из тех же элементов. Да, возможно получить автоматически реализуемую стратегию самосборки. Да, да, да…
Но, как и где должны появляться каналы связи, логические схемы, что должно быть толчком к началу процесса, пусть пока и спонтанного роста электронной схемы, реализуемого пока какими-то сказочными силами?
Ну, хорошо, плавают эти кусочки схем в каком-то замкнутом пространстве. И в какой-то момент, вдруг, сами, начинают организовываться в логическую структуру. Миллионы кусочков. Собрались, поработали, а потом … разобрались, и снова собрались, но … в другую схему. Все вместе или по частям, пока даже не важно. Как это можно организовать? Где и чем?
Понятно, что речь идет о микроразмерах и количествах в миллионах. Только тогда всё это имеет смысл. Трудно, но возможно. Для этого каждый кусочек электронной логики должен обладать сложностью, гораздо большей, чем та, для которой он предназначался вначале. Какими-то двигательными возможностями, какими-то средствами координации своего положения в пространстве, какими-то универсальными средствами контроля.
Сложность оказалась весьма приличная. [8] Это же электронная клетка. Автономный робот. На микроуровне.
И всё это только для того, чтобы реализовать самосборку логической структуры, сопоставимой с мозгом. Чтобы собрать миллиарды ячеек в одно целое, пригодное для логической обработки информации на среднем уровне.
А с другой стороны, самосборка в замкнутом объеме, по каким-то логическим законам, с возможностью постоянной перестройки и развития…
Да, заманчиво…
Хотя, не знаю. Нет у меня определенного ответа.
Но, такое свободное моделирование позволило выделить несколько счетных систем, наиболее подходящих для этой цели. Единичная, система Бергмана, коды Фибоначчи, … и только в отдельных случаях двоичная. Троичная система счета в этот перечень вообще не попала. А как же реализовывать многозначную, ну, хотя бы, троичную логику?
Может быть, пространственно. Один и тот же электрический потенциал в разных местах схемы может и обязан иметь разные логические оценки. Вот тут, это – ДА, там – НЕ ЗНАЮ, а вот там это уже – НЕТ.
И схема, как – никак, строится … в пространстве. Трехмерном.
Мы уже когда-то строили схемы взаимодействий разрядов в числе. Надо вернуться, и проверить. Ну конечно, опять те же системы. Единичная, Бергмана, коды Фибоначчи. У них пространство числа – объем. А вот двоичная система счисления объема не имеет. Просто линия разрядов.
И снова моделирование. Пространственные структуры числа в разных системах счисления. Число, это – единицы в пространстве. Единицы двигаются по осям, перепрыгивают с одной точки на другую, разбегаются и снова собираются в кучку…, и это все – числа. Где тут разряды, уже не очень понимается, осей в разные стороны – множество. Числа - объемные [31]. Как тут простейшие вычисления производить, непонятно. Но, всё в рамках правил, по законам математики.
Только, какой математики?
Так мы же сами создали эту математику. Абстрактную.
Ей должно быть всё равно, с какими единицами и в каком счетном пространстве работать. Все операции – разрядные. То есть, в пределах одного счетного разряда. Так мы сегодня и считаем. А вот где этот разряд находится, ей должно быть всё равно.
Только вот, немного диковато выглядят числа с несколькими разрядами одного уровня. Три разряда единиц, пять – десятков, еще пара – сотен…, и все они составляют одно число. А если количества одинаковых разрядов измеряются десятками и сотнями, или тысячами? Что-то крыша поехала….
Но, раз такие числа реализуются на бумаге, значит, они реализуются и в реальности. Объемные числа. А может это уже и не числа вовсе? Тогда, что это?
Считать человек начал именно с этого. С лунок, в которые он помещал камушки. Вот в этой столько, в этой - столько…, тогда число будет…, так рождалась когда-то разрядная система числа. Каждая лунка – разряд. И в ней должно быть меньше десятка. Если больше – перекладываем один камушек из десятка в следующую лунку, то, что больше десятка – обратно в эту, а остальные - в сторону. Вот она разрядная система организации счета. И «десяток» мог быть любым. Сколько определим. 2, 3, 5, …10, 12,…, всё это десяток, соответствующий основанию системы счета. Мы же это знаем.
Количество лунок для одного разряда, в принципе, ничем не ограничено. Сколько захотим - столько и накопаем. Сколько будет удобно для счета. Сегодня мы считаем, что удобно – одна лунка. А вчера? На заре математики. Тысячи лет назад?
Объемные числовые построения для разных систем счисления позволили реализовать геометрический принцип построения числа. И движение разрядных единиц стало происходить не только по одной разрядной оси, а по нескольким. В разные стороны. [31]
Что реализует это движение? Многозначную логику в одном объеме счетного пространства. Выход единицы в нужную точку определяет наличие того или иного логического ответа системы.
А само движение единиц в объеме, это – решение логической задачи. Направо – ДА, налево – НЕТ, прямо – НЕ ЗНАЮ…
Вполне реалистично.
На множество входов в этот объем мы подаем единичные импульсы, и в логическом объеме начинается движение. С одного триггера к другому через логические схемы…, в соответствии с правилами счета. Тут реализован двоичный счет, тут Ф-счет, там снова …
Технически все реализуемо, вполне. И задача, действительно, как-то там решается. Перестроили схему, и … можно решать другую задачу.
Вот, опять … перестроили. Кто и чем? В автономной системе это делать некому. Только сам.
И круг технической реализации логической системы на базе математической логики замкнулся.
В это же время была реализована модель счетной логики на базе двухразрядных ответов.[8] Как выяснилось позже, обобщение направления «dual rail». Есть такое вынужденное направление двухпроводного управления, в котором необходимость есть, а однозначной стандартизации нет. Ну, пусть будет такая…
Счетная логика – математическая. Реализует все логические действия в расширенном объеме. И, ИЛИ, НЕ… Как и двоичная логика, но лучше. Один минус – ответ двухразрядный: 00, 01, 10, 11.
Четыре разных логических состояния: ДА, НЕТ, НЕ ЗНАЮ, НЕТ ОТВЕТА. Для любой логической оценки хватит.
Логика рабочая, неопределенности состояний нет, всё считается. На эту логику вполне можно опереться, принять за основу. Но, … чем она лучше Булевой логики? Такая же математическая. Это и хорошо, и – плохо. Требует полноты исходной информации, не работает с неопределенностями. Стремится к однозначному логическому ответу. Для вычислительных машин пригодна, а для автономных логических систем? Да, большой вопрос…
Мы, сплошь и рядом сталкиваемся с неопределенностью, случайностью, с недостатком информации. Но наша логическая система вполне работоспособна в такой логической неразберихе. Как-то справляется со всем этим, и неплохо, очень неплохо. В этих неуловимо изменчивых условиях нашей реальности любая математическая логика медным тазом накроется, а наша, ничего, держится.
Как же она устроена? Будем искать…
И снова поиски…
Любая логика сначала должна реализовываться в автоматических операциях, проводимых на базовом уровне нулей и единиц. Значит, снова математическая логика. С дополнениями и отступлениями.
С одной стороны, да, автоматическая операция предполагает однозначные математические правила, независящие от условий и времени. Только так. Значит, математика обязана присутствовать в логических операциях.
Но, если отойти от общепринятых правил абстрактной математики, то математика может быть … разной.
Математика, такая, как она есть сейчас, это, по большей части, одна из логических систем. В этой системе приняты определенные правила и соглашения. Они нам кажутся очевидными постулатами, не требующими доказательства. Но это далеко не так.
Именно по этой причине существует и развивается философия математики, которая до сих пор ищет аргументы в пользу того или иного постулата, и контраргументы для их разрушения. Это помогает лучше сформулировать и уточнить самые основы математики. Почему на 0 делить нельзя? Что есть бесконечно малая и бесконечно большая величины? Что такое бесконечность, и можно ли к ней подходить как любому абстрактному множеству, т.е. например, возводить в степень или проводить счетные операции с бесконечностями?
Эти вопросы четкого ответа не имеют, хотя мы знаем множество правил, вроде бы, обязательного исполнения. Споры по этим и другим вопросам не утихают.
И ответ тут простой. Правила математики подчиняются правилам принятой системы логики. Они должны быть логичны. Для кого? Для нас, людей, в первую очередь. А будут ли они логичны для кошек, собак, обезьян и крокодилов, жучков и рыб? Вряд ли …
Не потому, что они математики не знают, а потому, что у них другая логика и другие правила. И математика, которая будет понятна им, должна быть построена на их логике. Но, другая логика рождает и другую математику. Какую? Спросить бы, да, не у кого…
Вот, та самая, другая математика и работает в логике автономных систем. Во всех живых системах. От клетки до человека.
И пока мы не поймем основ и правил этой всеобщей математики Живого, нам не построить реальной логики для понимания работы нашего мозга. А, значит, и не создать его работоспособной модели. Создаваемый нами искусственный мозг, построенный на принципах нашей математики, никогда не будет дружественным к нам, людям. Так что, перспективы тут не очень оптимистичные…
Надо искать и формулировать хотя бы начальные правила той, общей математики. Попробовал сформулировать [7]. Получилось интересно, но совершенно невообразимо, если подходить с нашими представлениями об основах математики. Но, когда попробовал эти правила обосновать, то вдруг понял – есть тут зерно истины. Обосновываются правила. И логически, и математически.
И все же, не хватает тут многого. Не ухватываю чего-то главного. Надо с другого конца попробовать. С основы жизни – ДНК.
К структуре ДНК и принципам её работы я возвращался много раз. [8] К основаниям, триплетам считывания, аминокислотам…
Почему основания парные? Почему считывание идет триплетами? Почему аминокислот только 20? Почему все говорят об избыточности триплетного кодирования, в чем она? Если избыточность кодирования есть, то почему 21-ая аминокислота (селеновая) с таким трудом умещается в ДНК? Для этого пришлось пожертвовать и старт-стоповым триплетом, и поменять немного систему считывания. Почему?
Потому, что нет никакой избыточности кодирования, а есть жесткая недостаточность. Не может клетка оперировать принятым в нашей математике понятием, что 43 = 64. Для клетки такая математика недоступна. У неё свои правила счета и свои возможности кодирования. По этим правилам 20 аминокислот с триплетным кодированием, это предел [8]. Вполне объективный.
При рассмотрении этого вопроса впервые были использованы основы новой математики. И как мне кажется, они вполне себя оправдали.
И снова возврат к основаниям ДНК. Почему оснований – четыре? Почему они парные? В тот раз я не смог разобраться. Но попытка не была совсем бесполезной. Кое-что я тогда понял. Но, к этому мы вернемся позже…
Блуждание в логиках.
Автоматические операции, выполняемые системой на самом нижнем, базовом уровне не давали мне покою. Ну сколько раз можно возвращаться к этим И, ИЛИ, НЕ… и не находить ответа. Единственная операция, которая никогда не вызывала сомнений в её необходимости – И. С остальными что-то всегда не получалось.
Больше всего вопросов возникло по поводу НЕ. В том виде, как она присутствует в сегодняшней двоичной логике, это не операция, и даже не функция. Если в первичной Булевой логике она имела смысл – получение противоположности для логического объекта, то сейчас и этот смысл утерян. Простой переворот фазы сигнала, и всё. Даже для двоичных чисел. Легким движением руки … брюки превращаются … в свою полную противоположность. Где тут логика?
Операция ИЛИ, так это же просто - все в кучу, кто первый - тот и вышел. А где же подразумеваемый выбор «или-или»? И где вообще, выбор, в базовых операциях?
Для организации выбора в автоматическом режиме нужно поменять направление движения. Нужен коммутатор или разветвитель. Это, чтобы вход был один, а выходов – не менее двух. Вот тогда – выбор. Или направо, или – налево…
Но, такой схемы в логических элементах нет.
Потому, что эта логика создавалась под математику. А вроде бы, должно было быть наоборот. Вот потому и не сходится эта математическая логика с нашей. Но, как сделано, так сделано, чего уж теперь…
Понятно, что эти критические замечания могут вызвать только ухмылку. Под эту математическую логику такой математический аппарат отгрохан - закачаешься, на этом всё программирование держится, да и все вычисления построены на этой логике. Тут поздно что-то менять.
Конечно. Тут – поздно. Тогда нужна другая логика.
И новый набор базовых операций. Вот уж тут-то можно всё учесть…
Но, для этого надо понять - что было, и что – надо. Это оказалось совсем не просто. Снова, математические логики:
Булева логика.
Троичная логика Н.Брусенцова
Счетная логика (симметричный и несимметричный варианты dual rail).
n- мерная логика.
Логика высказываний
Логика предикатов
Логика событий
Система базовых операций или функций, одна и та же. Выбирать не из чего. А подумать – есть. И пофилософствовать…
Что есть логика?
Без экскурса в историю. Без подглядывания в словари. Там всё понятно, умно и правильно. А вот если своими словами, жутко неправильно, но, все же, сформулировать свое ощущение. Логика, это …
Возможно, это способ в известных условиях найти обоснованный ответ на поставленный вопрос и принять решение? Возможно.
Или метод, как найти причину из условий имеющегося набора следствий? И это возможно.
Мы что-то сопоставляем, как-то выбираем наиболее обоснованные варианты, сравниваем, снова выбираем, и, наконец, принимаем решение. Да, это так.
Или не так? Мы крутим аргументы и факты, и так, и эдак, а ответ всё никак не находится. Почему-то ответов у нас всегда много, но нужен-то только один. Какой?
И мы снова идем по уже знакомому кругу. Нет однозначного ответа. И так можно сказать, и так, да и вот так – тоже. И все ответы будут правильными, не совсем, но …, вполне логичными. Все они чем-то подтверждаются, как-то обосновываются. Выбрать один очень непросто. А почему нам нужен только один ответ?
Или так. Задан простенький вопросик, например, почему небо - голубое?
И начинается…. Потому, потому и потому… и нет конца этому логическому ответу. Откуда берутся эти многочисленные «потому»? В вопросе их не было. Из чего они появились? Из простой связки: небо – голубое…
Мы, из двух слов построили целую цепочку связей, уходящую в бесконечность. Оценили связи, выбрали что-то, сравнили с чем-то, нашли наиболее важные, по ним задали себе вопросы, нашли ответы, и опять выбрали, сложили все результаты в одно изложение, сделали оценку уровня собеседника, скорректировали свои ответы на него и … наконец-то, начали излагать… логический ответ.
Да, ни одна принятая учеными система логики не справится с такой задачей самостоятельно…, ни одна. Почему?
Потому, что все системы логики одностороннего принципа действия. Они нацелены на … ответ. На систему разрешенных ответов.
В этом просматривается результат. И логичность принятых систем оценивается по степени адекватности получения именно такого результата. Ответ должен быть адекватен поставленному вопросу. И он должен быть обоснованным. Тогда он признается … логичным.
Конечно, если логика идет к результату через простые операции, то надо учитывать хотя бы вес того или иного ответа при отборе. Естественно, в ход идут вероятностные оценки. Да, с вероятностью 54% ..., вполне обоснованно, а нам что с этим ответом делать? Но, все экспертные системы работают так. Они выдают результат, а решать – нам.
И автоматические системы управления оценивают ситуацию точно так же, принимают решения, и действуют. Но наблюдатель-то им все равно нужен…, вот и сидим, контролируем действия, вмешиваемся…, помочь чаще всего уже не успеваем, но важный вид делаем. А потом исправляем последствия.
Что поделаешь, автоматика дала сбой.
Нет, это система логики дала сбой. Автоматика его только реализовала.
Так, что же такое – логика? Система правил, система мышления, система поиска ответа? Наверное…
Если есть система логик, сжимающих все возможные варианты ответов до набора разрешенных, то должна существовать и обратная ей.
Расширяющаяся логика [31], создающая из простой связки «небо – голубое» весь набор вариационных логических связей. Тот самый, уходящий в бесконечность…
Где эта часть логики? Может быть, забыли об этой, второй стороне, одной и той же логики…, логики, о которой мы говорим уже несколько тысяч лет?
Нет, не забыли. Скорее, спрятали.
Человек – венец Природы. Он – эталон. Его логика непогрешима, и оценкам не подлежит. Мы создаем системы логики для … слуг. А управление оставляем для себя. Мы принимаем решение. Они пусть работают по нашим системам, а мы их будем контролировать. Полная самостоятельность слуг никому не нужна и опасна. Компьютер, он, конечно, умный, но - слуга, и обязан делать то, что я от него требую. И не более.
Но вот требуем мы все больше. И стараемся навесить на наших слуг всё больше обязанностей, связанных с принятием решения, для последующих действий. Их действий, между прочим. Мы уже точно не успеваем, скорости уже давно не те, не наши…
Вот тут и вмешивается система логики. Основы, заложенные в неё, нами же.
Мы начинаем получать результаты наших действий.
Автоматика не учитывает нас, как хозяев. Она не дружественна нам. Она рациональна до абсурда. И мы вынуждены к ней, такой, приспосабливаться. И даже пытаться думать так же, однозначно. Парадокс.
Есть, о чем порассуждать.
Чем более адекватна логическая система в связке вопрос – ответ, тем более она дружественна нам, и более достоверна в отборе возможных ответов.
И совершенно прав Н. Брусенцов в оценке троичной логики. Она намного совершеннее булевой логики, более логична и более пригодна для основы автоматических систем. С другой стороны, она такая же, математическая, основана на тех же базовых операциях, и создана для вычислений. В общем, неплохая, со всех сторон. Но и тут прогресс прошел мимо. Почему?
Потому, что на этапе выбора троичная логика не сумела показать все свои достоинства, недостатки оказались более видимыми. Тогда. А сейчас?
Поздно. Снявши голову, по волосам не плачут. Выбор сделан.
Такая же участь постигла множество разработанных математических логик. Красивые решения предлагал, например, Льюис Керолл, но …
Логик математических, самых разных, много, а теория цифровых автоматов построена всё на той же, булевой логике…
Да что мы только о математических логиках, других, что ли, мало?
Хватает. На все случаи жизни. Одно перечисление займет страницу. Классические и неклассические. В основном - Модальные логики. Они все построены по одному образцу, вне зависимости от направления логики. Потому и рассматривались сразу все. В одном наборе [9].
Вот этот момент и есть основной. Общая схема решения.
Шаблонные схемы. Стандартные. Пригодны для любых логик и их вариантов. Они не учитывают конкретику, но образуют систему стандартных ситуаций при решении задач. Оказалось, что система ответов создает шаблонные схемы задач. И в нашей логике применены все основные системы ответов разных логических систем. В том числе и двоичной, и троичной, и многомерной логики. Как абсолютного, так и относительного определения. Вот тут и приложились к системам ответов модальные логики. Как тут и были всегда.
Да, к этим схемам нужно достойное приложение. Получается, что нет применения только для одной математической логики, а сразу и - все.
Потому и не получаются простые математические подходы к логическим операциям автоматического исполнения. И самое главное - любая логическая операция должна иметь и ответ, и результат.
Это означает, что каждое логическое действие должно быть закончено.
В этом коренное отличие от имеющихся математических логик с их функциями, выполняемыми мгновенно и одновременно. За один рабочий такт.
Открою Вам маленькую тайну: все наши математические логики никаких логических задач никогда не решали, и решать не будут. Потому, что это не логики, а системы одновременной коммутации импульсов. Потому, что все эти логические ответы ДА, НЕТ, НЕ ЗНАЮ, это только мимолетные рабочие состояния на контролируемых выводах нашей же электронной схемы. В начале и конце рабочего такта. Все это так.
Грустно?
Нет, не очень. Потому, что и человек на уровне ДНК устроен точно так же. Работает автоматическая программа, работает машинная логика автоматических операций внутри клетки. Нет там никакого интеллекта и разума. А вот отдаленный аналог компьютерной системы управления есть. Очень сложной системы. И безотказной, почти. Работает без перерывов всю жизнь, контролируется только иногда. Там работает почти такая же машинная логика неизвестной нам системы. И работает отлично.
Вот её и надо попытаться понять. Там те же машинные ДА, НЕТ, ..., что-то чему-то соответствует, но... та логика - автономная. Она сама определяет задачу, сама её решает, сама исполняет. В этом её коренное отличие от наших математических логик. И та же система логики работает на всех уровнях управления. Только задачи меняются, а принципы те же.
Логика должна работать в реальном времени. От результата к результату. Идти последовательными шагами. Использование параллельных решений, это уже расширение возможностей, а вначале мелкими шажками, чтобы было время на решение и остановку. На «подумать».
Нужна другая логика…
Начал с создания противоположности. Вместо имеющейся НЕ.
Это стержень решения всех логических задач. Создание противоположности во всех вариантах, это очень сложная и длительная задача. Потому и внимания ей отводилось много.
Потом была операция создания копии. Конечно, через противоположность. Также очень многоплановая составляющая всех решений. Копирование, это основа получения опыта, это продолжение Я, это повтор…. Классическая логика это не учитывает.
Далее были сравнение и выбор. Почему-то в математической логике этих операций нет. В программировании есть, а в логике – нет. Странно.
Уровень автоматических операций с объектами и ответами пройден. Теперь уровень простейших логических действий. Вот теперь события и условия. К нему я подбирался давно. С кучек и штучек. [8] Теперь, кажется, получилось…
Далее сделан переход на новый уровень. От объектов и ответов, к образам и эмоциям. Как мне показалось, это вполне закономерно.[9]
Система уровней оказалась вполне связной и взаимодополняющей. Какая получилась логическая система, это решать не мне. Но могу сказать, да, система получилась медленной, с массой промежуточных ответов и результатов. Решение идет через остановки, согласование одних результатов с другими в реальном времени. Это мне показалось самым важным для системы, решающей задачу без ориентиров, втемную. Тут надо три раза подумать, что бы сделать очередной шаг вперед. Но это только мое мнение …
Задачи и их решение в автономном режиме. С этим я кувыркаюсь уже давно. Что тут самое важное?
Способ представления задачи. Получаемый в конце решения ответ. Путь решения, который привел к правильному ответу. Приемы разворачивания задачи для понимания сути логической проблемы. Что?
Всё, кроме … ответа. Вот он оказался самым не важным. Система логических ответов нам известна изначально, до начала решения. Правильным может оказаться любой из разрешенных, и … что с того? Важно пройти весь путь и доказать обоснованность одного из ответов.
Вот это наличие пути и определило геометрический подход к формированию отображения хода решения. Он начал вырисовываться еще на этапе экспериментов со счетными системами. Понятно, что это графы [36], но есть несколько сложностей…
И тут случайность мешает. Как простыми методами учитывать случайные процессы при решении задачи? Снова и снова просматривал известные мне логики в надежде найти решение проблемы…
Но ничего не получалось. И вопрос не в том, что логики не подходят, а в том, что они слишком логичны для автономных логических систем самостоятельного развития.
Пришлось снова начинать с начала…
Нечеткая логика.
Лотфи Заде разрабатывал нечеткую логику для разрешения противоречия, известного давно:
«Наш основной тезис заключается в том, что по своей сути обычные количественные методы анализа систем непригодны для гуманистических систем и вообще любых систем, сравнимых по сложности с гуманистическими системами. В основе этого тезиса лежит то, что можно было бы назвать принципом несовместимости. Суть этого принципа можно выразить примерно так: чем сложнее система, тем менее мы способны дать точные и в то же время имеющие практическое значение суждения о её поведении. Для систем, сложность которых превосходит некоторый пороговый уровень, точность и практический смысл становятся почти исключающими друг друга характеристиками. Именно в этом смысле точный количественный анализ поведения гуманистических систем не имеет, по-видимому, большого практического значения в реальных социальных, экономических и других задачах, связанных с участием одного человека или группы людей.» [3]
Разрешить противоречие предлагается следующим образом: «Иной подход, развиваемый в этой работе, опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от «принадлежности к классу» и «непринадлежности» не скачкообразен, а непрерывен. И в самом деле, нечеткость, присущая процессу мышления человека, наводит на мысль о том, что в основе этого процесса лежит не традиционная двухзначная или даже многозначная логика, а логика с нечеткой истинностью, нечеткими связями и нечеткими правилами вывода. С нашей точки зрения именно такая нечеткая, еще недостаточно изученная логика играет основную роль в том, что может оказаться одной из наиболее важных сторон человеческого мышления – способности оценивать информацию, т.е. выбирать из давящего мозг разнообразия сведений те и только те, которые имеют отношение к анализируемой проблеме. По своей природе оценка является приближением. Во многих случаях достаточна весьма приближенная характеризация набора данных, поскольку в большинстве основных задач, решаемых человеком, не требуется высокая точность. Человеческий мозг использует допустимость такой неточности, кодируя информацию, «достаточную для задачи» (или «достаточную для решения») элементами нечетких множеств, которые лишь приближенно описывают исходные данные. Поток информации, поступающий в мозг через органы зрения, слуха, осязания и др., суживается, таким образом, в тонкую струйку информации, необходимой для решения поставленной задачи с минимальной степенью точности. Способность оперировать нечеткими множествами и вытекающая из неё способность оценивать информацию является одним из наиболее ценных качеств человеческого разума, которое фундаментальным образом отличает человеческий разум от так называемого машинного разума, приписываемого существующим вычислительным машинам.»[3].
Но, формулируя нечеткую логическую задачу в виде математических формул, Л.Заде подчеркивает: «Из последующих разделов будет видно, что теоретические основания нашего подхода на самом деле вполне точны и математичны по духу. Дело в том, что источником неопределенности в нашем подходе является не лежащая в его основе теория, а способы использования лингвистических переменных и нечетких алгоритмов в формулировании и решении реальных задач. В действительности, в каждом случае степень точности решения может быть согласована с требованиями задачи и точностью имеющихся данных. Подобная гибкость составляет одну из важных черт рассматриваемого метода.»[3].
Если говорить о формальной стороне, то нечеткая логика позволила получить математическое решение задач, например, модальных логик.
Лотфи Заде ввел в логику нечеткое множество, размытое множество [5] , тени [1] и грани [1], и т.д., а также множество новых математических символов и знаков.
Понятно удивление, с которым была встречена нечеткая логика. Неопределенность лингвистических оценок была уложена в математические каноны, вполне четко, несмотря на название предложенной логики. Последовала бурная реакция, попытки применения и … долгая тишина. Реальное применение принципов нечеткой логики было предложено только через много лет. И в весьма урезанном виде.
И только сейчас нечеткая логика начала новый виток развития. Сейчас уже широко применяются процессоры, реализующие принципы нечеткой логики в составе различных образцов бытовой техники. Это уже можно считать широким применением нечеткой логики, правда, с некоторой натяжкой. И все же, … применяем.
По этому пути и пошло применение его логики. И нечеткая логика превратилась в один из алгоритмов решений типовых задач. На основе экспертных оценок. Все остальные заявленные возможности потихоньку уходят в небытие. Возможно, что ненадолго. Время покажет.
С другой стороны, Лотфи Заде постарался решить задачи логики высокого уровня на уровне автоматических решений, видимо, противоречие, стоявшее перед ним в начале пути, показалось ему вполне решаемым на этом уровне.
И все же он так и не определил, каким образом происходит выбор и формирование исходного нечеткого множества, необходимого для решения задачи. Предполагается, что машина «знает» это, или критерии отбора известны изначально.
И потому, это пока делаем … мы, а задачу уже решает машина.
А мы как это делаем? Каким образом выбирается нужное множество, как мы подбираем фактики для начала, даже формулирования задачи, непонятно…
В своих последних работах [6] Л.Заде уже не возвращается к этому, ограничившись только математическим аппаратом решения. Но задача-то осталась…
Наверное, математически, нечеткая логика безупречна. Она позволяет сформулировать задачу в формуле, обосновать критерии оценки, провести вычисление и получить ответ в виде исполнительной команды. С другой стороны, весь аналитический материал подготовки задачи … формулируется и собирается вне логической системы проводящей решение задачи. Так, во всяком случае, было на стадии формирования нечеткой логики. Возможно, сейчас ситуация изменилась, но не очень сильно. Слишком большой объем информации и сложное математическое обеспечение надо иметь для проведения самостоятельных решений. Даже сейчас это проблематично.
Но задача поставлена и сформулирована правильно. Нечеткая логика находит достоверные решения. Видимо, принципы справедливы для всех типов логических систем, как отрытых, так и закрытых. Вопрос только в способности их применения…
Никакая автономная саморазвивающаяся логическая система не может, даже в принципе, освоить математический аппарат, предложенный для решения задач нечеткой логики. Если, правда, он не будет загружен в её память на стадии начального развития.
Но, это возможно только для машин, сооружаемых человеком, а что делать остальным … живым логическим системам. От клетки до … человека?
Да принципы есть, но … возможно есть и какой-то способ решения задач с другой основой принятия обоснованного решения. Без сложной многоуровневой математики, но не менее точный.
Хотя, мы всегда несколько предубежденно относимся к формулам математики. Интегралы и дифференциальное исчисление использовалось и тогда, когда они еще так не назывались. Многие вещи только понимаются сложно, а применяются везде и всюду, без осознания их истинной сложности. Мы очень часто проводим сложнейшие логические вычисления автоматически, не вдаваясь в подробности, как, собственно, мы это делаем…
При этом, математическое обоснование простейшего логического хода может занимать не одну страницу сложнейших формул. Это так.
С другой стороны, нечеткость исходной информации, неопределенность ситуации и жесткая необходимость поиска решения простейшими методами должна была отразиться на механизме поиска решения. В сторону его математической деградации, с сохранением точности конечного результата, пригодной для принятия конечного решения. Не имеет смысла математическая виртуозность, если результат нужен сразу и только на этот момент, иначе … он не нужен совсем.
Это, то самое противоречие в поиске эффективных решений, с которого начинал Лотфи Заде. С предложенным математическим аппаратом нечеткой логики оно сохраняется в полной мере.
Логическая система…на случайностях.
А почему бы и - нет? Очень даже может. И даже очень вероятно.
В конце концов, вся наша жизнь, это непрерывная цепь событий, в которых случайность играет далеко не последнюю роль. И более того, наложение случайностей, одна на другую, дает то неповторимое явление, которое мы называем своей жизнью. Она только моя, повторить её невозможно.
И уж если случайность так важна для нас, почему мы не можем положить её в основу всей логики Живого? Как одну из составных частей.
Для понимания случайности можно заглянуть, например, в [30]. Как оказалось, определение случайности всегда конкретно привязано к той науке, где она в данный момент изучается. В математике одно определение, в философии – другое…, с понятием неопределенности происходит примерно то же самое.
Тогда и я попробую дать свое понимание случайности и неопределенности.
Случайность, это когда мы не можем указать, что может произойти, когда и где…
Неопределенность знает, что должно произойти, но не знает когда и где…
Но, это, так, к слову…
Локализация случайностей.
Мы говорим, что беда не приходит одна, или, что надо ловить удачу за хвост…
Откуда это? Из народного опыта жизни…
А вот пример, технический. У вас вдруг пропал сигнал телеканала, а телевизор продолжает работать на этом канале. И на экране появляется характерная рябь случайных точек. Случайных, это мы точно можем сказать. Но вот что интересно, если внимательно приглядеться к этой случайной ряби, то вдруг оказывается, что она не совсем случайная. Ровной и пестрой картинки не получается. Точки группируются какими-то маленькими группами, постепенно двигаются по экрану в разных направлениях, как быстро движущиеся гусеницы, и все примерно равного размера…, изображение динамично изменяется… и при этом сохраняет общую картинку. Одинаковую на всех каналах…
По этой причине она очень хорошо запоминается.
Объясняется она просто. Вероятность образования, как полного хаоса, так и полного порядка, исчезающе мала. В этом противоположности сходятся. Почему?
Идеально ровное равнораспределенное поле из черных и белых точек на экране возможно только в случае появления … определенного порядка их чередования. Что маловероятно. Примерно такую же вероятность имеет появление на экране четких прямых линий из случайного шумового сигнала.
Наиболее вероятно появление вроде бы случайных небольших скоплений хаотичного расположения, наиболее вероятной плотности. Кучки черных и белых точек с нечеткими границами, и нечеткой локализации в поле экрана. Но случайность локализации, так же не может быть идеально равнораспределенной, и идет по критериям средней вероятности. Это означает только то, что каждый раз при смене кадра почти половина групп точек останется на месте. Как черных, так и белых. Они и создают примерный порядок на экране. Мы четко видим белые и черные, примерно одинаковые области, их «движение» по экрану. Остальное достраивает воображение. Но, в любом случае мы видим какой-то порядок там, где его вроде бы не должно быть.
Примерно, то же самое происходит и в жизни.
И действительно, как беды и несчастья, так и удачные периоды, обычно не заканчиваются на одном событии, а имеют групповой характер.
Так что, беда и счастье в одиночку, действительно, ходят редко…
Я вспомнил о локализации случайных величин неслучайно.
Понятно, что такой опыт не проводился, но все же …
Если сложить в каком-то объеме новенькие нервные клетки, еще не имеющие окончаний, и запустить процесс образования этих связей между клетками, то, что мы получим?
Мы получим совсем не случайную сеть из нервных связей, из аксонов и синапсов, идущих от нейронов в разных направлениях. Вполне локализованную, примерно равномерную структуру групп клеток, охваченных сильными связями внутри групп, и относительно редкими связями между группами…
Принцип тот же самый, что и локализация групп на экране телевизора, только скорости образования, конечно, меньшие, но результат предсказуем.
В случайном соединении логических связей мы увидим вполне логичный порядок.
Мелкие и крупные логические структуры, охваченные перекрестными, но относительно редкими длинными каналами связи. Полученная сеть вполне сопоставима с логическими схемами классических цифровых автоматов, хотя никто их заранее не планировал получить…
Наложение случайностей…
Странная это штука – случайность.
Несколько одновременных случайных процессов, происходящих вокруг нас, создают наложение их результатов в виде областей событий, как благоприятных, так и не очень, … для нас, проходящих через эту цепь случайностей.
Ю.В.Чайковский как-то констатировал: «Мы живем в мире случайностей, и они все время накладываются одна на другую» [28].
Есть одна неочевидность, о которой редко вспоминают. Теория вероятностей начинается с опыта. Например, бросание монетки. Какая вероятность, что выпадет «орел» или «решка»? Конечно, 0,5.
Можно ли сказать, что вероятность выпадения каждой из сторон монеты в каждый момент времени и при любом очередном броске одинакова? Нет.
Хотя, теоретически это должно быть так.
Оказывается, выпадение двух «орлов» или «решек» подряд более вероятно, чем их равномерное чередование. Проверить на опыте это очень просто. Надо провести серию бросков. Например, будем отмечать выпадение «решки» как (+1), а выпадение «орла», как (-1) . На графике серии будем отмечать результат последовательного суммирования всех проведенных бросков, вычитая или прибавляя по единице.
И окажется, что нулевой результат, т.е. совпадение теоретической вероятности с фактом, это явление чрезвычайно редкое. Итоговая линия результата будет выписывать сложную кривую, то и дело, уходя далеко, то в положительную, то в отрицательную область.
Конечно, такая явная несогласованность расчетной статистической вероятности и её реального исполнения, как в данном примере, давно привлекли внимание ученых. По этой теме проведено немало исследований…
Вот, что пишет об этом, например, Ю.В.Чайковский:
«Если само блуждание устойчивым распределением не описывается, встает вопрос – как его описывать. Основную информацию дает исследование «точек возврата» (точек, в которых траектория блуждания пересекает ось абсцисс, т.е., иными словами, моментов, когда доля гербов в точности равна 1/2). Точки возврата являют собой случайную величину, дискретное распределение которой задается формулой из которой видно – вероятность z того, что за время 2n траектория ровно r раз вернется к оси абсцисс, максимальна при r=o, r=1 и монотонно убывает при r>1 [Феллер, 1964, с. 97; Колмогоров и др., 1982, с. 89]. Тем самым, самые вероятные исходы блужданий – с одним пересечением или без единого пересечения, так что случайная величина, описывающая число возвратов неограниченно долгого блуждания, имеет монотонно падающую однохвостую плотность. Характер убывания весьма различен по r и по n, что видно из асимптотической формулы: Как видим, при данной длительности блуждания n вероятность иметь число возвратов r очень быстро убывает с ростом r, что и было отмечено в начале Введения: начавший проигрывать проигрывает с большой вероятностью и дальше. Казалось бы, вероятность z должна расти хотя бы с ростом длительности блуждания n, однако она при этом тоже убывает, пусть и очень медленно. И вот итог: «Чем продолжительнее серия бросаний, тем реже возвращения в нуль» [Феллер, 1964, c. 98].
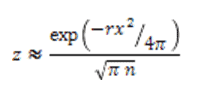
Эта цитата взята из [30].
Вроде мы говорим только об одной случайности. Какой стороной упадет подброшенная монета…, а разговор начинался о наложении случайностей.
Как же так? А вот так…
В простом опыте с бросанием монеты, мы, сами того не замечая, ввели второй случайный процесс. Суммирование результатов.
Теперь уже работают две связанные случайные величины: сторона монеты и… изменение суммы. И если сторона монеты имеет только два равновозможных варианта, то сумма результатов в своем распоряжении имеет … всю числовую ось. И точка 0, как совпадение расчетной вероятности с фактической, с каждым новым броском становится все менее вероятным исходом…
Парадокс, статистическое отклонение фактического значения от расчетной вероятности с каждым новым броском будет уменьшаться, а суммарное отклонение – нет.
Влияет ли каждый новый бросок на конечную сумму? Влияет, но чем больше бросков, тем меньше влияние. Когда бросков уже много, то весьма незначительно. И тем не менее, результат суммирования этих мелких случайностей может оказаться ошеломительным. А когда таких процессов суммирования несколько, и они идут одновременно, работая на общий результат, то какой он будет?
Непредсказуемый? Давайте, не будем торопиться с выводами…
Полный текст доступен в формате PDF (764Кб)
Никитин А.В., Логика автономных систем // «Академия Тринитаризма», М.,
|
|