|
|
|
Sokol-Kutylovskij O.L.
In the beginning of twentieth century classical natural philosophy ( classical physics ) was destroyed and replaced by so called non classic mathematical physics consisting of theor y of relativ ity and quantum mechanics. New non classic physics is based on postulates and faith, so it is more religion , than a scienc e. This article is a fragment of a new book in which development of natural ideas classical physics is presented.
1. The well-known thesis
There are two different types of mechanical motion in our infinite space: rectilinear motion and rotary motion or a turn. A change of mechanical motion of material bodies may be caused by means of physical forces. The gravitational forces differ from mechanical forces by distance of interaction: mechanical forces arise if contact interaction of bodies takes place and gravitational forces arise at remote gravitational interaction of bodies.
1.1. It is known, that the force arising between bodies in gravitational interaction, is directly proportional to mass of these bodies and in inverse proportion to a square of distance between them (law of universal gravitation or law of Newton):
| (1) |
where G– gravitational constant, m and M - masses of interacting bodies and r - shortest distance between centers of masses of bodies. If to s uppose , that the body of mass М on distance r creates a gravitational field of acceleration, directed to its center of gravity,
![]() ,
,
the force (1), acting on a body with mass m, may be presented as:
| (2) |
The force of Newton acts always both in a static s and in dynamics. T he forces of dynamic gravitational interaction are appearing a t change of movement of material bodies only .
1.2. We shall consider gravitational forces which act on a body, as a point, in which mass of a body or particle is concentrated. According to the modern theoretical mechanics, the complete force acting on the center of mass of a material body has the following kind:
| (3) |
where w - angular velocity of rotation of a body around of an axis which not crosses the center of mass of a bodies, v - velocity of linear movement of a body and r - radial vector connecting an axis of rotation of a particle or a body with the center of mass of a rotate body. The f irst force in equation (3) is gravitational force of Newton (2), second force in equation (3) is Coriolis force, and third force is centrifugal force. Coriolis force and centrifugal force are considered as fictitious force s which depend on frame . T hat not corresponds to all experience and elementary common sense. How possibl y to consider this physical force s as fictitious, if they can make real work? O bvious ly , that our knowledge about these forces are fictitious.
1.3. Angular velocity is an axial vector characterize d by some size and directed along the alone axis. The sign of direction of angular velocity is determined by right-handed screw. Angular velocity of rotation is a change of angle of turn in a unit time, ω (t)=¶ φ /¶ t . In this definition φ (t) - periodic function of time with the period 2 π . At the same time angular velocity is inverse function of time. T ime derivative of angular velocity: ¶ ω /¶ t=- ω 2 . Time derivative of angular velocity corresponds to the vector of angular acceleration. The axial vector of angular acceleration is directed along an axis of rotation, and to the same party, as angular velocity, if rotation accelerated, and against angular velocity, if rotation slowed down.
2. Gravitational forces, working on the center of mass of a body
2.1. Let us d etermine all gravitational forces act ing on the center of mass of material body. A s is well known f rom general principles of mechanics, the force arises at change of an instantaneous pulse of a body. B oth forces of linear movement of a body and forces of rotation mo tion of a body may be definit e by a similar way .
| (4) |
where v - instantaneous velocity of linear movement of a body, v ω – instantaneous velocity of a rotating of a body. As v ω =- rґ ω (Fig. 1), the equation (4) may be present ed as follows :
| (5) |
or:
| (6) |
In third member of the equation (6) the axial vector of angular velocity, ω , can be directed only along an axis of rotation and changes only by absolute value, therefore d ω /dt=¶ ω /¶ t , and in second member of the equation (6) the radial vector r can change both along the length and direction:
| (7) |
where r=r·[cos( ω t)·x + sin( ω t)·y ], x и y - unit vectors in a direction of the appropriate axes of coordinates, r - absolute value of a radial vector r, r1=r/r - unit vector in a direction of radial vector r, t - time, and the axis of coordinates z coincides with an axis of rotation. Time derivative of unit vector r1 is: ¶ r 1/¶ t= ω ·r 1^ , where r 1^ - unit vector situated in a plane of rotation and orthogonal to the radial vector r (Fig. 1).
Considering possible changes of a radial vector, according to the equation (7), the formula (6) has a view [1, 2]:
| (8) |
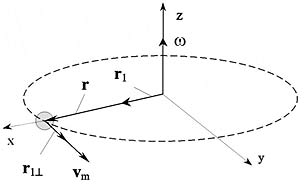
Fig. 1. Radial vector r, angular speed ω and instantaneous speed vm of a body of mass m in system of coordinates (x, y, z) with an axis of rotation directed along the axis z. Unit vector r1=r/r is orthogonal to unit vector r 1^ .
2.2. All forces which are included in the equation (8) are equal in rights. In short view the vector sum of forces (8) can be presented as four forces:
FG=Fa+ F ω1 + F ω2 + F ω3 .
The force Fа arises at the linear accelerated movement of a body or at gravitational static interaction of a body with other body. The force F ω1 corresponds to Coriolis force for a case, when the body move within the rotating system in radial direction ( along radius of rotation). This force is directed along instantaneous velocity of a body or against it. F orce F ω2 is acted on every point of rotating body. It is centrifugal force, but the same force is name d as Coriolis force, if the body in rotating system moves on a direction of instantaneous velocity, not changing absolute value of radius of rotation. The force F ω2 always is directed along radius. Taking into account equality ¶ r 1/¶ t= ω ·r 1^ , and direction of vector in vector product, we receive, that the force F ω2 = m· ω 2 ·r acts o n each point of a rotation body, so this force coincides with centrifugal force in the formula (3).
The force F ω3 is a force of inertia of rotary movement [1, 2].
| (9) |
The force of inertia of rotary movement arises at change of angular velocity of rotating system and it is directed along vector of instantaneous velocity of a body at dw /dt <0 and against vector of instantaneous velocity of a body at dw /dt >0. Th is force arises only at transients, but at uniform rotation of a body this force is absent. A direction of gravitational force of inertia of rotary movement is shown o n Fig. 2. Here r - radial vector connecting on the shortest way an axis of rotation with the center of mass of a rotating body, ω - axial vector of angular velocity.
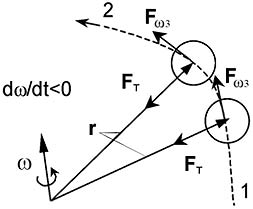
Fig. 2. A direction of gravitational force of inertia of rotary movement, F ω3 , at moving a body from a point 1 to a point 2 at dw /dt<0; r – radial vector connecting an axis of rotation with the centre of mass of a moving body; FT – attractive force or force of a tension of a rope. The centrifugal force is not shown.
The sum of forces F ω1 and F ω2 creates resultant force ( Coriolis force FK) at movement of a body in any direction in rotating system:
| (10) |
where v - vector of velocity of a body moving in side rotating system. From the equation (10) follows, that numerical factor «2» is not present in Coriolis force.
The sum of gravitational forces act ing on the center of mass of a firm body has a view [1, 2]:
| (11) |
3. Gravitational and mechanical forces, arising at turn of an axis of rotation of a body
To determine all gravitational forces act ing on any point of a material body (not only on the center of mass) it is necessary to return to the formula (5).
The formula (5) which was receiv ed from general principles of the mechanics contains all forces act ing on any point of a rotating body, including forces arising at spatial turn of an own axis of rotation of this body. Therefore from the formula (5 ) it is possible to find the equation for force act ing on any point of a rotating material body at a turn of its own axis of rotation. For this purpose we must present the equation (5) as follows:
| (12) |
where Ѕ rґwЅ - the absolute value of a vector rґw , and (rґw )1 - unit vector directed along vector rґw . As indicated above , time derivative o f vector rґw gives gravitational and mechanical forces of rotary movement: centrifugal force, Coriolis force and force of inertia of rotary movement:
| (13) |
where m - mass of a body, r1 - the unit vector conterminous with vector r by direction.
From the formula (12), in view of the formula (13), follows, that the complete sum of all gravitational forces consists of five components [1, 2]:
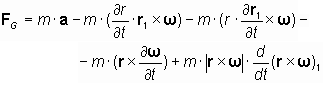 , , |
(14) |
where fifth component is a force, more precisely, a set of forces arising at spatial turn of an axis of rotation of a body in all points of this body. In brief view the complete sum of all gravitational forces may be written as:
| (15) |
where Fa - force of Newton with a gravitational vector of acceleration a, Fw 1 - Fw 3 - forces of rotary movement with a gravitational vector of angular velocity w and е FwW i - the forces arising at a turn of an axis of rotation of a body in all n points, on which a body by regular intervals is divided .
Fifth component can be presented in detailed kind. Radial vector r is orthogonal to the vector of angular velocity w , therefore absolute value of a vector rґw is equal to product of absolute values of these vectors:
![]() .
.
Time derivative of unit vector (rґw )1 at change on direction gives other unit vector, r 1 , located parallel to plane of turn S (x, z) and orthogonal to the vector rґw (Fig. 3). A t this case the coefficient , which numerically is equal to time derivative of angle j , W =¶j /¶ t , is appear s :
| (16) |
As a movement of points of a body at a turn of an axis of rotation is three-dimensional, and the turn of an axis occurs in some plane S (x, z), the absolute value of an unit vector concerning a plane of turn is not constant, and changes from zero to 1. Length of an unit vector (rґw )1 concerning a plane of a turn S (x, z) is the projection of this unit vector o n a plane of turn. Derivative of unit vector (rґw )1 in plane of turn S (x, z) can be submitted as:
| (17) |
where a - angle between a vector rґ w and plane of turn S (x, z).
The force act ing on any point of a rotating body at turn of its axis of rotation is enclosed not to the center of mass of this body, but to each given point. Therefore body necessary to divide on set of points, and to consider, that each such point has mass mi. Mass of the given point of a body, mi, is meant as mass concentrated in small on the relation to all body volume Vi so, that:
![]() .
.
When density of a body r is uniform , mass mi=r ∙Vi , and point of the appendix of force is the center of mass of given part of volume Vi of material body, occupied by a part of mass mi. The force act ing on each a point of a rotating body at a turn of its axis of rotation has a view:
| (18) |
where mi - weight of the given point of a body, ri - shortest distance from the given point (in which force is defined) up to an axis of rotation of a body, w - angular velocity of rotation of a body, W - absolute value of angular velocity of turn of an axis of rotation, a - angle between a vector rґw and plane of turn S (x, z), and r 1 - unit vector parallel to a plane of turn and orthogonal to the vector of instantaneous velocity rґw .
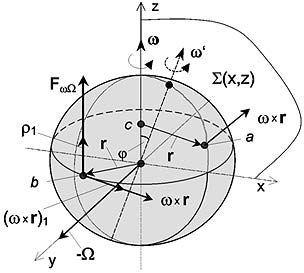
Fig. 3. Direction of force Fw W arising at turn of rotation of axis of a body in a plane S (x, z) with angular velocity of turn, W . In a point a the force Fw W =0; in a point b the force Fw W has maximal value.
The sum of all forces (18), acting on all n points, on which a body in is divided through regular intervals,
| (19) |
creates the moment of forces turning a body in the plane Y (y, z), orthogonal to plane of turn S (x, z).
Existence of forces (19) is known, but they were not precisely determined. In particular, in the theory of gyroscope these forces are named as «gyroscopic forces», but the origin of these physical forces is not opened.
From property of symmetry follows, for each point of a body corresponds to other point which is located symmetrical to axis of rotation, where force s (18) have same value , but opposite direction. The joint action of such symmetric pairs of forces at turn of an axis of a rotating body creates the moment of forces turning this body in the third plane Y (y, z), which orthogonal to a plane of turn S (x, z) and planes L (x, y) , in which occurs rotation of points of a body:
| (20) |
Thus for unit vectors of angular velocity in any of points of a body which not co incide with center of symmetry (by the center of mass ), the next vector equality is carried out:
| (21) |
where Q 1 – unit vector of angular velocity arising at the moment of action of force (18), w 1 – unit vector of angular velocity of rotation of a body and W 1 – unit vector of angular velocity of turn of an axis of rotation (Fig. 2). Because of axis of turn conterminous to a vector of angular velocity of the turn W , always ортогональна of an axis of rotation conterminous to a vector of angular velocity of rotation of a body, w , a vector of angular velocity Q always ортогонален to vectors w and W : ![]() .
.
The interrelation of angular velocities at free rotation of a body on the three mutually orthogonal axes can be found, by applying the law of preservation of energy of rotary movement. In the elementary case for a homogeneous body of weight m in the form of a sphere with radius r we have:
![]() ,
,
or ![]() .
.
4. Complete sum of primary gravitational and mechanical forces acting on a body
4.1. The complete equation o f the sum of all gravitational forces act ing on any point of a material body, participating in linear and rotary movement, including spatial turn of an own axis of rotation, has the following view [1, 2]:
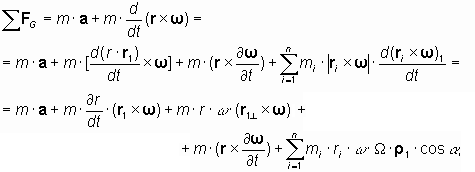 |
(22) |
where a - vector of linear acceleration of a body with mass m, r - radial vector connecting an axis of rotation of a body with a point of the appendix of force, r - absolute value of a radial vector r, r1 - unit vector direct ed along radi al vector r, w - angular velocity of rotation of a body, Ѕ rґwЅ - absolute value of vector of instantaneous velocity rґw , (rґw )1 - unit vector direct ed along vector rґw , r1^ -unit vector located in a plane of rotation and orthogonal to vectorr1, W - the absolute value of angular velocity of turn of an axis of rotation, r 1 - unit vector directed parallel to a plane of turn and orthogonal to the vector of instantaneous velocity rґw , a - angle between a vector rґw and plane of turn, mi - mass of «i» -point of a body concentrated in small volume of a body, Vi, which is a center of application of force, and n - the numbers of points, on which a body is divided. In the formula (22) the sign of forces can be taken positive, as these forces in the general formula are under the sign of absolute value. The sign of forces may be defined by direction of each concrete force. With the help of forces which are included in the formula (22), it is possible to describe mechanical movement of any point of a material body at its movement on any trajectory, including spatial turn of its axis of rotation.
4.2. So, in gravitational interaction there are only five various physical forces act ing on the center of mass and on each of points of a material body at rectilinear and rotary mo tion of this body and only one of these forces can act on a motionless body. T aking into account of all forces of gravitational interaction allows understanding stability of mechanical dynamic systems, and with adding of electromagnetic forces - stability of atoms.
Literature
- Sokol-Kutylovskij O.L. Gravitational and electromagnetic forces. Ekaterinburg, 2005 (On Russian).
- Sokol-Kutylovskij O.L. Russian physics. Ekaterinburg, 2006 (On Russian).
Sokol-Kutylovskij O.L., Gravitational forces // «Академия Тринитаризма», М.,
|
|