Институт Золотого сечения - Философия Гармонии

Сергиенко П.Я.

Всё существующее имеет меру

Математические начала – это знания о том, как, посредством мер геометрии и числа, Единое (континуум пространства-времени Вселенной) обретает континуумно-дискретное ¹ множество объектов и как эти множества сохраняют содержание и форму целостности континуума. ¹

Современная математика, пользующаяся огромным доверием других наук, в действительности не заслуживает такого доверия. «В самом деле, рассуждает В.А.Успенский ², считается общепризнанным, что математика имеет, по крайней мере, следующие три присущие только ей черты. Во-первых, в математике, в отличие от других наук, все понятия строго определяются. Во-вторых, в математике — опять-таки в отличие от других наук — все строго доказывается из аксиом. В-третьих, математика непонятна в такой вызывающей уважительный трепет степени, какая недоступна ни одной другой науке». Современная математика выстроена на довольно зыбком фундаменте понятий. Мы обнаруживаем, что одно понятие определяется через другое, другое через третье и т. д. Подлинно глубокое математическое понятие или математическое утверждение, по мнению Успенского, должно быть в своей сути просто. То есть математические понятия должны выражать собой простоту принципов, присущих вечному сохранению и развитию Природы и принцип наименьшего действия, обеспечивающий единство сохранения и развития. Суть этой простоты выражается в общих понятиях: сколько прибавится, столько и отнимется; сколько умножится, столько и разделится. Данная простота приоритета принципа сохранения над принципом развития, принцип их гармоничного синтеза и наименьшего действия были заложены уже в началах математики пифагорейцев. Напомним, исследуя НАЧАЛА математики, пифагорейцы пришли к следующему заключению:

- арифметика не может служить основой для геометрии;

- геометрические величины имеют более общую природу, чем числа и их отношения;

- в основу математики следует положить геометрию. Так родилась в античные времена геометрическая алгебра, посредством которой исчислялись длины, площади и объемы.

Евклид обобщил семивековые наработки математических знаний пифагорейцев и платоников. Он в III в. построил геометрию пустого бесконечного пространства и дал математическое описание его свойств. Свои результаты Евклид изложил в знаменитой книге «Начала», которая без каких-либо изменений использовалась в качестве основного учебного пособия по геометрии вплоть до XX столетия.

Пространство, по Евклиду (позже оно так и было названо «евклидовым»), безграничное, однородное, изотропное (от греч. «изос» — «равный», «одинаковый» и «тропос» — «направление»), имеет три измерения. Бесконечность такого пространства характеризуется тремя постулатами:

1) «от всякой точки до всякой точки можно провести прямую линию»;

2) «ограниченную прямую можно непрерывно продолжать по прямой»;

3) «из всякого центра и всяким раствором можно описать круг».

Несколько позже Архимед выделил еще одно свойство евклидова пространства, в котором «из всех линий, имеющих одни и те же концы, прямая будет наикратчайшей».

Таким образом, в евклидовой геометрии прямая линия представляет собой геодезическую линию, т. е. линию с наименьшей длиной. Пространство, характеризующееся этим свойством, является по современной терминологии плоским пространством, т. е. обладает нулевой кривизной. Его метрика (квадрат расстояния между двумя близкими точками) в декартовой системе координат имеет вид: ds² = dx² + dy² + dz², где dx, dy, dz — бесконечно малые приращения координат х, у, z.

Построенная Евклидом геометрическая теория пространства имела огромное значение не только для развития математики и физики, но и для культуры в целом. Знание основ евклидовой геометрии стало необходимым элементом современного общего образования во всём мире. Почти через 2 тыс. лет после создания, теория евклидова пространства без каких-либо изменений была взята Ньютоном в качестве математической модели абсолютного пространства в его механической картине мира. Евклидово пространство является ареной всех физических явлений классической физики, основы которой заложили Галилей и Ньютон.

В заключение краткого исторического обзора резюмируем: геометрия Евклида – геометрия пространства пустоты, геометрия идеально прямых линий и идеального кругового движения, которые в Природе проявляются, как частные случаи всеобщего бытия.

ИЗНАЧАЛЬНЫЕ МЕРЫ САКРАЛЬНОЙ ГЕОМЕТРИИ

Является ли точка изначальной мерой всего? Проблема понимания и пространственного представления точки – возможно, самая сложная. Сложная потому, что точка выступает неким началом и мерой отсчета ступени познания той или иной материальной или идеальной системы бытия действительности. В согласии с пифагорейским учением, Всё есть число…, а онтологическим основанием числа является некая геометрическая величина, как изначальная (элементарная) мера бытия ВСЕГО. Какая же геометрическая величина является истинно элементарной мерой бытия ВСЕГО, или – «порождающей моделью» ВСЕГО, по Платону? Данная проблема не имеет решения до настоящего времени.

Традиционно принято полагать, что движение нулевой точки порождает одномерную линию, движение линии порождает двумерную поверхность, а движение поверхности, порождает трехмерное тело. Таким образом, в согласии с данной логикой, изначальной (элементарной) мерой всего математического бытия является геометрическая точка. Исключительное свойство геометрии точечного пространства, согласно изначальному постулату, оно «не имеет меры». Данное понятие геометрической точки противоречит аксиоме «Всё существующее имеет меру». Известно, что любые понятия и вкладываемый в них смысл с течением времени меняются и, к сожалению, не упрощаются, а усложняются. Например, философское решение понятийного противоречия точки, по принципу определения одних понятий через другие привело, к очень усложненному понятию точки вообще. Образцом такого усложнения может служить, например, нижеследующее диалектическое обобщение философски-математических представлений о точке профессора М.Р.Шарипова.

«Крайним представлением об элементе является точка − абсолютная актуальность, т.е. явный (явленный) носитель отношений реализовавшегося противоречия предыдущей структуры и результат оконечивания последующего процессуального или потенциального процесса, искусственно устраняющего последующую структуру системы в результате устранения её потенциальной (процессуальной) акциденции, структурно-смежно (диалектически) соединённой с необходимой действительностью. В этом смысле, точка как форма нового качества предыдущих структур, является бесформенным носителем этого качества в абстракции последующих структур. С другой стороны, в силу относительности формы и содержания, точка – бессодержательная форма, если её качество обратить в форму относительно последующих структур, т.е. точка – пустая идея относительно последующей структуры искусственно лишённая той потенциальной акциденции её последующего развития, которая и осуществляет актуализацию целостной возможности пустой идеи в элемент этой структуры. Сказанное относится также к математическим представлениям о прямой, плоскости и многообразии с неустранимым процессуальным или диалектическим противоречием формы и содержания, актуального и потенциального. Ясно, появление противоречий в этом случае обусловлено тем, что несчётные совокупности точек, минуя процессуальность или диалектичность потенциальной бесконечности, могут явить абстракцию пространства этих точек как абстракцию актуального объекта, наделённого искусственно введёнными конечными структурно-смежными отношениями как проявлением свойств их несчётных совокупностей и не имеющих отношения к истинному процессуальному или диалектическому развитию развёртывающихся конкретных структурных звеньев Мироздания, представляющих процесс синтеза возможного – случайного – виртуального – необходимого, т.е. единство многообразного. Такая реальность совокупностей точечных элементов и форм встречается лишь в структурах математических моделей. Поэтому, пространство как математический образ – это объединение несчётного множества актуальных объектов в абстрактный образ ещё неявленной (по сути, виртуальной) и оконеченной процессуальной или потенциальной структуры необходимой действительности с устранённой процессуальной или потенциальной акциденцией. (Развитие этого представления о пространстве проливает свет на сущность и осознанную противоречивость континуум -гипотезы)» ³.

А проливает ли, данное понимание «точки», свет на ее сущность и сущность «континуума» – это еще большой вопрос. Давайте вернемся к объекту нашего исследования, т.е. – к геометрической точке.

Геометрия изучает пространственные свойства предметов, оставляя в стороне все остальные их признаки. Например, резиновый мяч диаметром в 25 см и чугунное ядро того же диаметра отличаются друг от друга по химическому составу, по плотности, по упругости, по весу, по цвету, по твердости и т. д. Однако, все отличительные признаки мяча и ядра в геометрии оставляются без внимания. Пространственные же их свойства (форма и размеры) одинаковы. С точки зрения геометрии, каждый из этих предметов представляет собой только шар диаметром 25 см.

Предмет, от которого мысленно отняты все его свойства, кроме пространственных, называется геометрическим телом. Шар есть одно из геометрических тел. Идя дальше по пути отвлечения, мы получаем понятия геометрической поверхности, геометрической линии и геометрической точки. Поверхность мы мысленно отделяем от тела, которому она принадлежит, и лишаем ее толщины. Линию мы лишаем толщины и ширины, а точку вовсе лишаем измерений. Мы мыслим, что точка может служить границей линии (или ее части), линия — границей поверхности и поверхность — границей тела. Мы мыслим также, что точка может двигаться и своим движением порождать линию, линия может движением порождать поверхность, а поверхность — порождать тело.

В природе нет точек, лишенных измерений, но есть предметы столь малых размеров, что их в некоторых условиях можно принять за геометрические точки. В природе нет также ни геометрических линий, ни геометрических поверхностей, но все свойства линий и поверхностей, найденные в геометрии, находят многообразные применения в науке и технике. Это происходит потому, что геометрические понятия порождены пространственными свойствами действительного мира. Отвлеченная форма геометрических понятий для того и служит, чтобы эти свойства изучать в чистом их виде. А то, что мы вовсе лишая измерений точку вступаем в противоречие с Истиной геометрического бытия точки, как-то ранее никому не приходило в голову.

Бытие геометрической точки по определению, как не имеющей меры, самостоятельно не проявляется и не существует. Геометрическая точка, как не имеющая меры, то есть, как «нулевая точка», проявляется и существует исключительно, как пересечение двух перпендикулярных (ортогональных) линий, не имеющих ширины. Она может служить началом отсчета меры для длины любого отрезка, как будучи неподвижной, так и, находясь в движении.

Таким образом, Геометрическая точка, не имеющая меры – частный случай из бесконечного многообразия точек, порождаемых пересечениями линий под другими углами. Поскольку линия имеет меру длины, то все точки, образуемые пересечением линий под любым углом, кроме пересечения их под прямым углом, имеют меру длины отрезков линий. В триалектике такие геометрические объекты, имеют синтетические понятия «точка-линия» и «линия-точка». Первое понятие говорит о том, что точка пересечения линий обретает форму линии, а второе – форму точки.

Следовательно, изначальной мерой и «порождающей моделью» ВСЕГО бесконечного многообразия геометрических объектов, порождаемых круговым движением, является отрезок прямой линии, приравненный единице.

Математика гармонии– это математика, изучающая и моделирующая гармонию бытияпространственно-временных форм Жизни и их количественные отношения, проявляющиеся в эволюции природы, общества и мышления ⁴.

Синтез научных и сакральных математических знаний Запада и Востока о мироустройстве и их современное переосмысление позволяют заложить НАЧАЛА «синтетической» и «сакральной» геометрий, которые в свою очередь закладывают основание математики гармонии.

Сакральная геометрия принципиально отличается от алгебраической геометрии тем, что метрика ее объектов обозначается и выражается не абстрактными символами (буквами), а конкретными рационально-иррациональными числами (точки пересечения так же обозначаются цифрами). В сакральной геометрии отсутствует такое понятие, как произвольная точка, поскольку в геометрической действительности, как самостоятельный объект, точка не существует. Следует отметить, что с введением в геометрию понятия «произвольная точка», был как бы узаконен «произвол» геометрических фантазий человека, которые не соответствуют природной действительности. Такой фантазией, например, является учение о параллельных прямых, порожденное знаменитым пятым постулатом Евклида. В настоящее время он формулируется так: через любую точку, не лежащую на прямой, можно провести одну и только одну прямую, параллельную данной прямой. Еще раз повторимся: точка, не имеющая меры, вне линии существовать в действительности не может, а существующая на линии, имеет меру отрезка линии, сколь угодно большого и сколь угодно малого.

Из всех известных геометрий, только сакральная геометрия позволяет нам осуществлять конкретные гармонические построения геометрических фигур, выражать их в непосредственных и относительно масштабных числовых мерах.

Таким образом, суть начал сакральной геометрии сводится к решению конкретных задач построения рационально-ирациональных чисел как геометрических объектов. При этом нужно учесть, что НАЧАПА «сакральной геометрии» синтезируют в себе понимание мира бытия чисел Пифагором (пифагорейцами) и Платоном (неоплатониками). У Платона роль сакрального начала принадлежит «круговому движению» (Рис.1), а у Пифагора – равностороннему треугольнику, так называемому «тетрактису» (Рис.2).

Все математические операции «доказуемости» равенства геометрических объектов осуществляются посредством арифметических операций с числами. Выше были указаны изначальные числовые меры гармоничного деления, сложения, вычитания, умножения и извлечения квадратного корня: 0,5, 1,1180339…, 0,6180339…, 1,6180339…, 0,1180339… 1,2360678… и другие. Следовательно, наша задача – геометрическое построение на прямой линии указанных чисел.

ИЗНАЧАЛЬНЫЕ ИНСТРУМЕНТЫ ГЕОМЕТРИЧЕСКОГО ПОСТРОЕНИЯ
РАЦИОНАЛЬНО-ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ

Природа, по мнению Платона, в построении форм тех или иных движущихся тел, пользуется мерой линии кругового движения. Что это за мера, Платон не уточнил. По мнению Евклида, мерой построения круга является «раствор», которым «из всякого центра» можно его построить. Под всяким центром Евклид подразумевает произвольную, «нулевую» точку. В сакральной геометрии «нулевая» точка, обозначаемая «0» («не число») – безмерное начало концов отрезка. Любой отрезок в нулевой степени есть «1».

Для геометрического построения рационально-иррациональных мер гармонии, в согласии с принципом наименьшего действия, Природа пользуется минимумом присущих ей законов, их свойств и осуществляет любое построение так же минимумом математических (геометрических) действий. Человек, следуя примеру Природы, для геометрического построения рационально-иррациональных чисел так же должен стремиться к минимальному набору соответствующих механических инструментов, позволяющих строить множество прямых линий и их пересечений, множество окружностей, множество эллипсов и делить с их помощью пополам отрезки линий.

Самыми древними инструментами, с помощью которых строились такие огромные и строго гармоничные сооружения как, например, Египетские пирамиды, являлись: не обладающий растягиванием канат с сочлененными концами и три палки (колышка). Это были первые будущие линейка и циркуль.

Натянутый, сочлененный канат между двумя, зафиксированными колышками, образует две параллельных, условно равных и прямых линии.

Натянутый канат между тремя, зафиксированными колышками, образует линии треугольника. Число разных треугольников (острых, прямых и тупых) может быть неисчерпаемо, поскольку тремя колышками линия сочлененного каната может делиться на бесконечное множество разных по величине трех отрезков, сумма которых – величина всегда постоянная.

Древние геометры два колышка использовали для построения окружности (круга), а три – для построения многообразных форм эллипсов. При построении эллипсов они использовали уже расчлененный канат, имеющий на концах петли. Один из трех колышков (гвоздиков на нашем рисунке) использовался как чертилка (карандаш) эллипса. Замкнутая симметричная линия, где сумма удалений любой ее точки от двух заданных есть величина постоянная, называется эллипс.

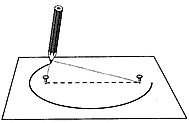Рис. 1. Построение эллипса

Форма эллиптической линии, описывается двумя постоянными мерами: длиной линии каната и угловым раствором натяжения каната между ее неподвижными концами, так называемым, «фокусным» расстоянием между ними. Слово focus в переводе с латинского означает «огонь». Если расстояние между забитыми гвоздиками (Рис.1) будет равно «0», то карандаш будет чертить эллипс имя которому – окружность. Если расстояние между фокусами равно длине каната, эллипс превращается в отрезок линии, равный двум радиусам или диаметру окружности, образуемой тем же канатом при фокусном расстоянии равном «0».

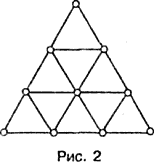
Указанными на Рис.1 инструментами строится так же главная сакральная геометрическая фигура пифагорейцев – равносторонний треугольник, названный ими «тетрактисом». Тетрактис делится десятью точками пересечения линий на девять равносторонних треугольников, олицетворяющих собой Всемирную полноту Монады монад и Животворящий Свет (рис. 2). Каждый из 9-ти треугольников являет собой изоморфную монаду изначальной монаде и аналогично в свою очередь может быть разделен так же на изоморфные треугольники и т.д. Можно полагать, что пифагорейская Монада является основанием фрактальной геометрии. Изучая Рис.2, мы замечаем, что точки «тетрактиса» принадлежат линиям, а не точки образуют линии, как полагает Евклид.

Синтезировав философские учения об онтологии математических (геометрических) начал Платона и Пифагора, автору удалось создать или, возможно, возродить утерянные еще в древности знания геометрического построения чисел математической гармонии, перечисленных А.П.Стаховым. Разумеется, я не могу утверждать, что предлагаемый ниже, метод построения является единственным и, что демонстрируемые геометрические построения полностью ковариантные методу, и принципу наименьшего действия, которыми пользуется Природа.

Изначальной мерой (единицей («1») меры) в построениях сакральной геометрии принята сторона произвольного «тетрактиса» пифагорейцев, который они полагали Монадой монад.

НАЧАЛА СИМВОЛИКИ САКРАЛЬНОЙ ГЕОМЕТРИИ

В построениях сакральной геометрии все точки пересечения обозначаются цифрами: 1, 2, 3, …, 10, 11,… Отрезки обозначаются цифрами точек, разделенными дефисом, при этом левая цифра меньше правой. Например, отрезки: 1-4; 1-7; 1-9 (Рис.3). При возведении геометрических величин в степень, умножении, делении и вычитании отрезков, обозначаемые отрезки заключаются в скобки. Периметры многоугольников обозначаются аналогично. Например, треугольники: 1-4-6; 1-2-4; 0-1-2. Цифры треугольника, начинающиеся с «0» свидетельствуют, что треугольник – прямоугольный.

МЕТОД ГЕОМЕТРИЧЕСКОГО ПОСТРОЕНИЯ
РАЦИОНАЛЬНО-ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ
НА ЧИСЛОВОЙ ОСИ

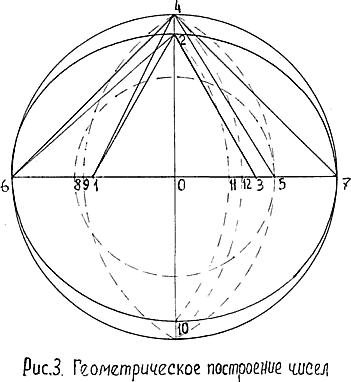1. Строим вышеуказанным способом на Рис.1 равносторон­ний треуголь­ник («тетрактис») 1-2-3. Его стороны: 1-2 = 1-3 = 2-3 = 1.
2. С вершины треугольника 1-2-3 восстанавливаем пер­пен­ди­ку­ляр 0-2 к стороне треугольника 1-3, пере­се­ка­ющей ее в точке «0», которая делит отрезок 1-3 на половин­ные части и, таким образом, строим вещественное число «0,5».
3. Строим эллипс фокусным расстоянием 1-2 = 1.
4. Строим окружность ра­диу­сом 0-4 = 1-3 = 1.
5. Продолжаем отрезки 1-3 и 0-2 до их пересечения с окружностью в точках 4, 6, 7, где 0-4 = 1, а 6-7 = 2.
6. Соединяем точки 4, 6 прямыми линиями и строим прямоугольный равно­бед­рен­ный треугольник 4-6-7, площадь которого равна половине вписанного в круг квадрата. В согласии с теоремой Пифагора, находим число стороны квадрата 4-6:

(1).

7. Вычисляем построенный отрезок 1-4, который является гипотенузой прямоугольного треугольника 0-1-4:

(1-4)² = (0-1)² + (0-4)²; (1-4)² = 0,25 + 1 = 1,25; 1-4 = (2).

8. Раствором циркуля 1-4 чертим круговую линию, которая пересекает диаметр круга 6-7 в точке 5. В итоге полученный отрезок 1-5 равен отрезку 1-4. То есть отрезок 1-5 ≈ 1,1180339.

9. Вычтя из отрезка 1-5 длину отрезка 0-1, мы получаем длину отрезка 0-5:

1,1180339 – 0,5 ≈ 0,6180339 (3).

10. Прибавив к отрезку 1-5 длину отрезка 1-6, мы получаем длину отрезка 5-6:

1,1180339 + 0,5 ≈ 1,6180339 (4).

11. Раствором циркуля 0-5 чертим окружность и отсекаем на диаметре круга сакральный отрезок 5-8, который равен ≈ 0,6180339 х 2 ≈ 1,2360678 (5).

12. Вычтя из отрезка 0-7 длину отрезка 0-5, мы получаем длину отрезка 5-7:

1 — 0,6180339 ≈ 0,3819661 (6).

13. Вычтя из отрезка 0-5 длину отрезка 0-3, мы получаем длину отрезка 3-5:

0,6180339 – 0,5 ≈ 0,1180339 (7).

14. Точку 4 соединяем прямой с точкой 5 и в согласии с теоремой Пифагора вычисляем отрезок 4-5:

(4-5)² = (0-5)² + (0-4)²; (4-5)² ≈ 0,3819661 + 1 ≈ 1,3819661; 4-5 . Переносим на прямую круговым движением отрезок 4-5 = 5-9 ≈ 1,1755705 (8).

15. Вычисляем построенный отрезок 6-4, который является гипотенузой прямоугольного треугольника 0-4-6:

(4-6)² = (0-6)² + (0-4)²; (4-6)² = 1 + 1 = 2; 4-6 = . Переносим на прямую линию круговым движением отрезок 4-6 = 6-12 ≈ 1,4142135 (9).

16. Вычисляем высоту «тетрактиса» 0-2 из прямоугольного треугольника 0-1-2:

(0-2)² = (1-2)² — (0-1)²; (0-2)² = 1 – 0,25 = 0,75; 0-2 = (10).

В нашем синтезированном построении сторона «тетрактиса» является одновременно радиусом круга, фокусным расстоянием эллипса и большей его полуосью. А высота тетрактиса является меньшей полуосью эллипса и равна половине стороны правильного треугольника, вписанного в построенный круг. То есть меньшая ось эллипса 2-10 равна стороне правильного треугольника, вписанного в эллипс-круг: 0,8660254х2 ≈ 1,7320508 = (11).

17. Вычисляем построенный отрезок 2-6, который является гипотенузой прямоугольного треугольника 0-4-6 и переносим его круговым движением на прямую линию, где 6-11 = 2-6:

(6-11)² = (0-6)² + (0-2)²; (6-11)² = 1 + (0,8660254)²; 6-11 = (12).

Построенные выше геометрически на одной прямой рационально-иррациональные числа позволяют также определить в рационально-иррациональных числах длину отрезков 1-9; 8-9; 11-12; 3-11; 3-12; 1-11 и других.

Таким образом, НАЧАЛА «сакральной геометрии», являющейся основанием математики гармонии, базирующейся на единстве принципов сохранения и изменения, а также на принципе наименьшего действия, думается, заложены.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ.

Примечания

•  ¹⁾  Континуум (лат. continuum - непрерывное) - непрерывная совокупность. Дискретность (от лат.discretus - разделённый, прерывистый) - прерывность.

Литература

•  ¹⁾  Сергиенко П.Я. Триалектический синтез начал познания // "Академия Тринитаризма", М., Эл № 77-6567, публ.11823, 14.02.2005.
•  ²⁾ Успенский В.А. Семь размышлений на темы философии математики // "Академия Тринитаризма", М., Эл № 77-6567, публ.11127, 08.04.2004
•  ³⁾ Шарипов М.Р. Философские основания понятия пустоты (пустое множество) // "Академия Тринитаризма", М., Эл № 77-6567, публ.12285, 22.07.2005
•  ⁴⁾ Сергиенко П.Я. О математике гармонии и порождающей ее модели // "Академия Тринитаризма", М., Эл № 77-6567, публ.12463, 28.09.2005

[Обсуждение на форуме «Наука»]