Напомню, в конце «Беседы 5» читателю была предложенадилемма – какой же прямоугольник, составленный из 4-х прямоугольных треугольников, вписанных в данный круг, является равновеликим ему по площади. Тот прямоугольник, площадь которого , или же тот, площадь которого ? Обратите внимание, речь идет не о равновеликой площади квадрата данному кругу, а – о равновеликой площади прямоугольника данному кругу. Существует ли обозначенная дилемма? Если да, то как она решается?

Выстраивая ответы на поставленные вопросы, начну с истории ее возникновения. После публикации моей брошюры 1997 г. [2] было много отзывов и продолжаются споры по поводу двух значений числа «пи». При этом некоторые оппоненты отмечали, что проблема не нова, она известна была еще в глубокой древности. Исследуя проблему НАЧАЛ, я как говорится, по призванию обязан был решать, а не обходить эту сложную проблему. В этой связи позволю себе процитировать фрагмент из моей публикации 2001 г. [3].

«Оппоненты данного решения (1997 г. – П.С.) резонно замечают, что автор не доказал того, что квадрат, построенный на хорде АВ – равновелик данному кругу. Заметим и мы, чтобы опровергнуть доказательство автора о том, что S = π₂r², требуется доказать, что существует некая другая хорда x (геометрическая мера) данного круга, удовлетворяющая алгебраическое уравнение π = x²/r², и тем самим вычислить более точно π. Теперь зададимся вопросом. Правомерно ли ставить знак числового равенства между разными геометрическими отношениями (мерами):

x²/r² = J/r²= u/2r =3,14159…, [1]

или же данные отношения имеют разные числовые значения? Действительно ли равновелик, построенный автором, квадрат данному кругу? В этой связи необходимо рассмотреть проявление некоторых геометрических закономерностей, которые вносят дополнительную ясность в логику вкладываемых смыслов в решение задачи квадратуры круга и упоминаемых в папирусе Ринда «тайнах». Коротко перечислим их.

1. Общеизвестно, что при равных периметрах правильных многоугольников, занимает относительно большую площадь тот многоугольник, степень кривизны периметра (число сторон) у которого больше. Самую большую площадь при равенстве периметров занимает многоугольник, как бы «выродившийся» в круг, при бесконечном удвоении его сторон.

2. Периметр окружности круга является пределом уменьшения (описанного) или увеличения длины периметра вписанного многоугольника при бесконечном удвоении его сторон. То есть около окружности можно описать и в нее можно вписать правильный многоугольник. Центры вписанного и описанного многоугольников лежат в центре окружности. Апофемой описанного многоугольника является радиус окружности, вокруг которой описан многоугольник.

3. При бесконечном удвоении сторон, апофема вписанного многоугольника никогда не достигает длины радиуса. Когда она достигает его длины, то скачкообразно становится уже апофемой описанного многоугольника. Сущность перехода одного в другое являет для нас тайну.

В согласии с существующими аксиомами математики площадь правильного многоугольника равна произведению полупериметра на апофему. Площадь круга равна произведению полуокружности на радиус. То есть площадь круга вычисляется аналогично вычислению площади правильного многоугольника.

4. При бесконечном удвоении сторон, пределом периметров. описанного вокруг окружности и вписанного в нее многоугольников, будет одна и та же окружность данного круга. При следовании к данному единому пределу геометрической формы, каждый из многоугольников обладает разными, если можно так выразиться, «стартовыми» данными: у описанного вокруг круга многоугольника уменьшается только его периметр, а у вписанного — увеличиваются длина апофемы и периметра.

5. Равенство площадей круга и вписанного многоугольника может быть достигнуто только тогда, когда станут равными их периметры. Однако здесь есть одно противоречие между известным допущением математики и действительностью: в реальности параметры (апофема, периметр и площадь) вписанного в окружность многоугольника не могут достичь параметров (радиуса, периметра и площади) круга. Как только апофема становится равной радиусу, многоугольник становится описанным. Утверждать, что он становится кругом, значит отказаться от трансцендентности числа «пи».

6. Равенство площадей круга и описанного многоугольника вокруг данного круга, при бесконечном удвоении его сторон, в согласии с выделенным выше жирным шрифтом условием, должно наступить еще до момента достижения «слияния» периметра многоугольника с периметром круга. То есть существование данного равенства, в отличие от первого, не вступает в противоречие с действительностью. Из этого вытекают следующие следствия: а). Периметр у равновеликого описанного многоугольника по площади данному кругу, при бесконечном удвоении числа его сторон, будет всегда больше периметра данного круга; б). Площадь круга вычисляется аналогично вычислению площади правильного описанного многоугольника: в). В согласии с формулой площади круга, константа отношения площади круга к квадрату своего радиуса будет иметь большую величину, чем значение константы π₁ = 3,14159...; г). Существует некая «числовая константа (поправочный коэффициент) отношения между круговой и квадратной мерами поверхности».

Из перечисленных геометрических закономерностей и их следствий возникают разные дополнительные вопросы теоретического и практического содержания. Возникает практический вопрос. Какой константой мы должны пользоваться при вычислении площади круга, поверхности цилиндра и объема цилиндра? Разница между числовыми значениями констант π₂ — π₁=3,14644 – 3,14159=0.00485…, что составляет около 0,154%. За данными числовыми значениями скрыты многие тайны природы, бытия и творения жизни, информации, выделения и поглощения энергии и т.д. При этом еще раз заметим, что суждения оппонентов о моем способе решения задачи квадратуры круга являются диаметрально-противоположными. Одни признают факт решения задачи «квадратуры круга», как она сформулирована в папирусе Ринда, другие отрицают, разумеется, не бездоказательно. Резонно полагать, что истина находится где-то посредине. Из каких начал (крайних значений числа π) мы должны исходить, чтобы максимально приблизиться к ней?»

По истечении еще двух лет исследований я пришел к выводу, что решить многовековой спор можно исходя из начал «золотой пропорции» и «золотого сечения». В итоге, по ходу решения проблемы на указанных началах, она обернулась дилеммой.

Чтобы решить возникшую дилемму, нам необходимо в последовательных геометрических преобразованиях (изменениях) круга в разные фигуры (треугольник, прямоугольник и квадрат) соблюдать два важнейших принципа присущих Природе – принцип сохранения и принцип наименьшего действия. Первый принцип требует сохранения длины периметра круга и образуемых из него других геометрических фигур. Второй принцип требует минимум операций преобразования.

Для решения дилеммы необходимо руководствоваться положениями трех аксиом.

Увеличить >>>

Аксиома 1. Прямоугольников, равновеликих по периметру данному кругу и разных при этом по площади, может существовать сколь угодно много. Аксиома 2. Прямоугольник, равновеликий по периметру данному кругу, у которого все стороны равны – квадрат и существует в единственном числе. Аксиома 3. При равных периметрах прямоугольников площадь больше у того прямоугольника, у которого меньше разница между его периметром и периметром равновеликого ему квадрата.

В конечном итоге, дилемма решается фактически на основаниях «Аксиомы 3», так как при указанной разности периметров равной «0» прямоугольник становится квадратом.

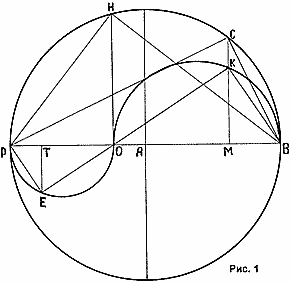
Рассмотрим Рис.1. РСВ – «сакральный треугольник». Основные его параметры мы уже знаем из «Беседы 5». Четыре сакральных треугольника образуют прямоугольник, у которого одна сторона равна 1,7989074r, а другая сторона равна 2ВС ≈ 1,7480638r и площадь его равна . Соответственно, периметр образуемого прямоугольника, равновеликого по площади данному кругу, равен 2РС + 4ВС ≈ 7,0939424r. Сторона равновеликого ему по площади квадрата . Соответственно, периметр равновеликого по площади квадрата равен 1,7733034r ∙ 4 ≈ 7,0932136r. Разница между периметрами равновеликих прямоугольника и квадрата равна 7,0939424r - 7,0932136r ≈ 0,0007288r.

Читателю известен из «Беседы 4» прямоугольный треугольник, построенный автором, один из катетов которого ≈ 1,7724538r (второй катет ≈ 0,9265028r). Таким образом, автор построил сторону «квадрата равновеликого данному кругу» с фантастической точностью. Можно праздновать победу, или же построить по тому же принципу равновеликий квадрат с еще большей точностью на два-три порядка… Однако, посмотрим какой складывается прямоугольник из 4-х построенных прямоугольных треугольников:

2 ∙ 1,7724538r + 4 ∙ 0,9265028r ≈ 7,2509188r;

Периметр же равновеликого ему по площади квадрата равен 1,7724538r ∙ 4 ≈ 7,0898152r. Разница между периметрами равновеликих по площади прямоугольника и квадрата равна 7,2509188r - 7,0898152r ≈ 0,1611036r.

В итоге, на основании сравнения периметров равновеликих прямоугольников и квадратов, имеющих значения и , доказано, что разница между периметрами первого и второго выражается неравенством: 0,0007288r <0,1611036r.

Таким образом, посредством сравнения двух прямоугольных треугольников, вписанных в данный круг, у которых катеты соответственно равны ≈ 1,7733034r и ≈ 1,7724538r и последующего их преобразования в равновеликие кругу прямоугольники, на основании «Аксиом 2 и 3» осуществлены следующие доказательства:

1. Прямоугольник, площадь которого 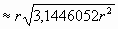является по своей геометрической форме, если можно так сказать, больше квадратом равновеликим данному кругу, нежели равновеликим данному кругу прямоугольником.
2. Прямоугольник, площадь которого 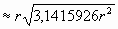, по сравнению с прямоугольником (п.1), является по своей геометрической форме больше прямоугольником равновеликим данному кругу, нежели равновеликим данному кругу квадратом.
3. Вывод: площадь равновеликого квадрата данному кругу, а соответственно и площадь круга, больше значения 3,1415926…r². Практически площадь круга равна 3,1446052…r².

Приведенные доказательства посредством конкретной меры и вычислений вносят в существующие знания и познание метрических закономерностей Природы существенные коррективы, игнорирование которых наукой недопустимо.

В заключение рассмотрим параметры вписанного в данный круг прямоугольного треугольника РНВ. По построению: ОВ ≈ 1,2360678r, РО ≈ 2r — 1,2360678r ≈ 0,7639322r. Высота НО прямоугольного треугольника , а его площадь ≈ 0,9717365r². Катет НВ ≈ 1,5723025r. 1,5723025r ∙ 4 ≈ 6,28921r. То есть НВ – сторона квадрата, периметр которого численно равновелик площади круга ≈ 3,144605r². Площадь же квадрата равновеликого по периметру кругу ≈ (1,5723025r)² ≈ 2,4721351r². Отношение площадей квадрата и круга дают нам удивительным образом безразмерное число равное числам высоты МС и площади «сакрального треугольника» РСВ: 2,4721351r² : 3,144605r² ≈ 0,7861513. Удивительны и другие отношения: РН = ОВ ≈ 1,2360678r; РН : РО = 1,2360678r : 0,7639322r ≈ 1,6180339. И здесь мы встречаемся с удивительными мерами отношений и параметрами отношений, поскольку имеем дело с мерами уже обратной проекции, проекций прямых линий на сферическую поверхность. Далее мы переходим к познанию геометрии 6-мерного, торсионного пространства-времени.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ

1. Ф.Рудио. О квадратуре круга. Москва 1934 – Ленинград.
2. Сергиенко П.Я. Задача квадратуры круга и ее решение. Пущино – 1997, 22 с.
3. Сергиенко П.Я. Триалектика. О мерах мудрости и мудрости мер. Пущино – 2001, с. 44-51.
4. Сергиенко П.Я. Начала. Триалектика сакральной геометрии//Тезисное изложение. Пущино – 2005. 32 с.