САКРАЛЬНЫЙ ТРЕУГОЛЬНИК

В «Беседе 2» по озаглавленной проблеме я доказал «Теорему 4». Этим доказательством фактически открыт геометрический принцип наименьшего действия кругового (циклического) движения присущего всей Природе. Там же я привел пример о вычислении площади вписанного прямоугольного треугольника, в согласии с данным принципом. Если гипотенуза прямоугольного треугольника делится на гармоничные части 1,6180339r и 0,3819661r, то его площадь составляет четверть площади данного круга и, в соответствии с «Теоремой 4», равна:

Рассмотрим подробнее порядок построения и параметры «сакрального треугольника».

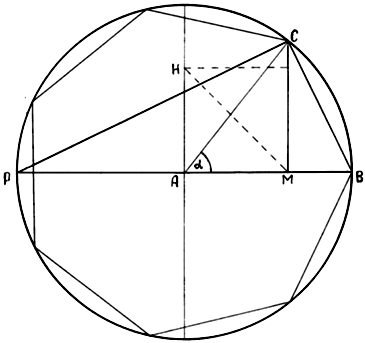
Рис. 1

Порядок построения сакрального треугольника до рассечения диаметра круга на части 1,6180339r и 0,3819661r выполняется (Рис. 1) так же, как и при геометрическом решении задачи «золотого» сечения отрезка (см. «Беседа 3»). Поэтому, чтобы не загромождать рисунок, последовательность выполнения всех предшествующих операций построения «золотого» сечения опустим.

После определения точки «золотого» сечения М, в точку М восстанавливаем перпендикуляр. Соединяем концы диаметра круга Р и В с точкой С (точка пересечения линий перпендикуляра и периметра круга) прямыми РС и ВС. Таким образом, мы построили искомый сакральный треугольник РСВ. Почему ΔРСВ я назвал «сакральным», читателю станет понятным после вычисления его параметров и связанных с ними др.геометрических отношений.

ФЕНОМЕНАЛЬНЫЕ ПАРАМЕТРЫ САКРАЛЬНОГО ТРЕУГОЛЬНИКА:

1. Площадь треугольника РСВ равна среднему геометрическому значений «золотого сечения» диаметра круга:
   
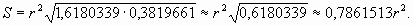
2. Высота СМ треугольника РСВ численно равна его площади. То есть высота треугольника 0,7861513r = равна его площади 0,7861513r².
3. Произведение 0,7861513r²•4 ≈ 3,1446052 r², свидетельствует о том, что:
   а) площадь круга практически равна сумме четырех площадей, вписанных в круг, прямоугольных треугольника ВРС с точностью до ≈0,0030126r² (≈0,0959%), если сравненивать с существующей теоретической площадью круга (3,1415926…r²);
   б) площадь треугольника ВРС практически равна четверти площади круга, в который он вписан.
   
4. Построим с помощью циркуля и линейки квадрат равновеликий по площади четырем «сакральным» треугольникам и приближенно равновеликий площади данного круга (Рис. 2).

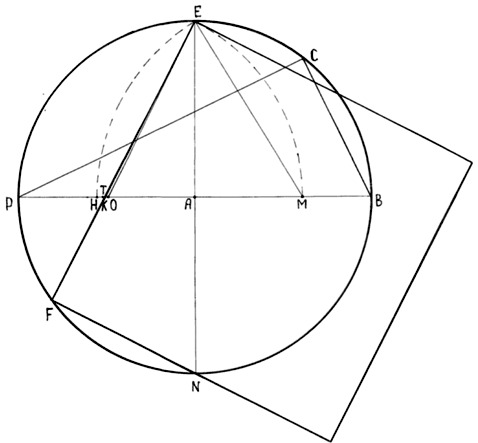
Рис. 2. Квадрат приближенно равновеликий площади данного круга.

Производим следующие операции построения и вычисления:

• раствором циркуля ЕМ ≈ 1,1755704r, из точки М чертим дугу до пересечения ее с диаметром ВР в точке Н и получаем отрезок НМ = ЕМ ≈ 1,1755704r;
  

• отрезок НО = НМ – ОМ. НО ≈ 1,1755704r – 1,1180339r ≈ 0,0575365r. НО делим пополам и получаем отрезок ТО ≈ 0,0287682r;
  

• отрезок ТО делим пополам и получаем отрезок длиной ≈ 0,0143841r, который также делим пополам и получаем слева от точки О отрезок длиной H 0,0071926r;
  

• с помощью циркуля складываем последний и предпоследний отрезки и получаем отрезок КО ≈ 0,0143841r + 0,0071926r ≈ 0,0215761r.
  

• вычисляем длину отрезка АК: АК = КО + АО; АК ≈ 0,0215761r + 0,5r ≈ 0,5215761r;
  

• с точки Е через точку К проводим прямую до пересечения ее с периметром круга в точке F;
  

• соединяем точки F и N прямой линией.
  

Таким образом, мы начертили прямоугольный треугольник EFN. Предполагается, что катет EF – сторона квадрата, который равен данному кругу. Проверим наше предположение. Для этого рассмотрим треугольники EFN и ЕКА. Углы у них равны, а стороны находящиеся против равных углов пропорциональны. То есть FN : AK = EN : EK.

В согласии с теоремой Пифагора вычислим ЕК:

В согласии с пропорцией вычисляем длину катета FN прямоугольного треугольника EFN:

FN = (0,5215761r 2r) : 1,1275452r ≈ 0,9249047r.

Вычисляем сторону квадрата EF, приближенно равновеликого площади данного круга:

5. Сторона ВС треугольника РСВ (Рис.1) является стороной правильного 7-угольника.

В согласии с утверждениями, содержащимися в математической энциклопедии: «Древние умели делить круг на 2, 3, 4, 5, 6, 8, 10, 12, 15 частей. Вообще, правильный 2п угольник можно получить из правильного п-угольника путем деления пополам дуг, на которые вершины n-угольника разбивают его описанную окружность. Таким способом на основе k-угольника легко построить все (2ⁿ•k)-угольники…

Построить правильные 7- и 9-угольник нельзя — при этом возникают неразрешимые в квадратных радикалах кубические уравнения…» [ 1 ].

Не знаю построения 9-угольника, но построением, осуществленным в согласии с Рис. 1, существующее утверждение – «построить правильный 7-угольник нельзя», опровергается.

Докажем, что сторона ВС треугольника РВС – действительно сторона правильного 7-угольника. Для этого условно разделим окружность на 7 равных частей в градусных мерах: 360^о : 7 ≈ 51^о36’.

Соединим прямой точки А и С и рассмотрим треугольники АСВ и АСМ у которых общий угол α ≈ 51^о36’. Треугольник АСМ – прямоугольный, у которого АМ = 0.6180339r, MC = 0,7861513r, АС = r Sin51^о36’ ≈ 0,78615r. Соответственно Сверим наше доказательство другим методом, т.е. по вычислению стороны треугольника – РС.

6. Диагональ НМ (Рис.1) квадрата, сторона которого равна 0,6180339r данного круга, равна стороне правильного семиугольника ВС:

7. Радиус круга АС (Рис.1) делит треугольник РВС на два равных по площади треугольника. То есть площадь треугольника АРС равна площади треугольника АВС.

Чтобы доказать это, по известным уже параметрам Рис.1 вычислим площадь треугольника АВС, которая равна сумме площадей прямоугольных треугольников АМС и ВМС:

• площадь треугольника АМС равна 0,5 х 0,6180339r х 0,7861513r ≈ 0,242934r²;
  

• площадь треугольника ВМС равна 0,5 х 0,3819661r х 0,7861513r ≈ 0,1501415r²;
  

• площадь треугольника АВС равна 0,1501415r² + 0,242934r² ≈ 0,3930755r²;
  

• площадь треугольника АРС равна 0,7861513r² – 0,3930755r² ≈ 0,3930758r².
  

Таким образом, мы доказали, что площадь треугольника АВС равна площади треугольника АРС.

8. Общая высота МС (Рис.1) треугольников АВС и ВРС делит площади треугольников АВС, ВРС, АМС, ВМС на гармоничные части относительно друг друга:

АВС : АМС = 0,3930755r² : 0,242934r² ≈ 1,618034;

ВМС : АВС = 0,1501415r² : 0,3930755r² ≈ 0,381966;

АМС : ВРС = 0,242934r² : 0,7861513r² ≈ 0,3090168;

ВРС : ВМС = 0,7861513r² : 0,1501415r² ≈ 5,2360693;

ВМС : АМС = 0,1501415r² : 0,242934r² ≈ 0,618034 и т.д.

НАУЧНАЯ ДИЛЕММА

Возникает естественный вопрос – какими параметрами обладает прямоугольный треугольник площадью ≈ 0,785398r² (≈3,1415926r² : 4)? То есть, на какие пропорциональные части необходимо разделить диаметр данного круга, чтобы построить прямоугольный треугольник, площадь которого равна четверти площади ≈3,1415926r²? После длительного поиска удалось вычислить, что у аналогичного прямоугольного треугольника высота МС делит его гипотенузу на части:

1,6189908…r и 0,3810092…r. Чтобы убедиться в этом, вычисляем высоту прямоугольного треугольника, которая численно равна одной четвертой части площади данного круга: Данное число умножаем на 4.

0,78539816r•4 ≈ 3,14159264r – число существующей «теоретической» площади круга. Заметим, что феноменальных параметров, при дальнейшем исследовании, у «теоретического» треугольника не обнаруживается.

Таким образом, феноменальные параметры «сакрального» прямоугольного треугольника, высота которого делит основание в соотношении «золотого сечения» ставят перед исследователем научную дилемму – какой же прямоугольник, составленный из 4-х прямоугольных треугольников, является равновеликим по площади данному кругу. Площадь, которого равна: ? или же, площадь которого равна: ?

Как же разрешить возникшую дилемму выбора правильного решения задачи «квадратуры» круга? Об этом и другом – в очередной «Беседе».

ЛИТЕРАТУРА:

1. Энциклопедия для детей. Том 11, математика, М., «Аванта+»,1998, с. 316.
   
2. Сергиенко П.Я. Начала. Триалектика сакральной геометрии. Пущино – 2005. 32 с.