|
|
|
Пименов Р.И.
1. Постановка вопроса.
В последние десятилетия в физике и около физики много толкуют [1] о смене парадигмы, о поисках по-настоящему сумасшедшей теории, словом, выражают неудовлетворение сложившимся экспликативным инструментарием. Особенно заметным стало это после того, как пригожинский подход к кинетике химических реакций стал рассматриваться как АЛЬТЕРНАТИВА каноническому физическому видению. После того, как проблема объяснения высокой организованности живой природы стала рассматриваться НА ФOHE энтропийной организации природы физической и, соответственно, превратилась в проблему объяснения самоорганизации живого из неживого. Мы не намерены входить ни в решение этой проблемы (или объяснять, что это псевдопроблема), ни в обзор решений этой проблемы. Мы хотим заняться более частным, можно даже сказать «узким» вопросом, который однако входит неотъемлемой составной частью в общую проблему, как знает каждый. Именно, мы займемся вопросом о ПРИМЕНИМОСТИ ДИФФЕРЕHЦИАЛЬНЫХ УРАВНЕНИЙ. Ведь уже подробностями мелкого порядка выглядят колебания: пользоваться ли дифференциальными уравнениями ЛИНЕЙНЫМИ (как обычно в физике) или же HEЛИНЕЙНЫМИ, например, третьего порядка (как И.Пригожин). Это вроде как пользоваться попавшей в словари частью русского языка и непопавшею, – но язык-то все равно русский!
Использование дифференциальных уравнений с самого начала было сопряжено с идеей устойчивых законов природы, пользуясь знанием которых можно было бы ОДНОЗНАЧНО ПРЕДСКАЗЫВАТЬ БУДУЩЕЕ. Иными словами – с детерминацией настоящим будущего. Опять же мы не станем вдаваться в описание отличия такого математического предсказания от предсказаний астрологических, жреческих, индуктивных, идущих от тайного знания, нормативных и т.п. Соответствующая самая общая и законченная постановка вопроса была дана Лапласом и получила название «лапласовский детерминизм». Но о самой крайней и всеобъемлющей постановке мы тоже будем говорить мало, нас будет интересовать умеренная применимость идеи детерминации в более ограниченной форме.
Общая связь между дифференциальным уравнением и детерминацией такова. Пусть u(t)–некоторая физическая переменная, зависящая отвремени, мызнаем ее значение u(t0) в начальный момент t=t0 и знаем закон du/dt = a (1) в форме дифференциального уравнения, которым управляется величина u(t) всегда, во все моменты времени. Тогда математические теоремы говорят, что u(t) в любую, дату t>t0 определяется ОДНОЗНАЧНО т.е. детерминированно (при соблюдении определенных технических условий, обсуждать кои здесь неуместно). Для той-то цели и ищут-пишут в физике дифференциальние уравнения, чтобы иметь возможность потом оперировать с переменной u(t) как с однозначной, как с данной.
2. Обходы проблемы.
Этот подход подвергался критике с разных сторон и выросли иные разделы физики, в которых такое воззрение суть физических процессов так или иначе отвергалось, По времени, пожалуй, первым был статистический подход. Не сомневаясь в принципе, что каждая молекула газа или жидкости движется по траекториям, детерминированным в этом смысле, всплескивали руками от необозримости множества этих траекторий и явной немыслимости учесть их все для описания движения струи газа; так возникал статистический, вероятностный подход.
Вероятность же возникала и в квантовой физике, где никак невозможно детерминировать, через какую щель пойдет электрон. Где допускается лишь посредством ВЕРОЯТНОСТНОЙ волновой функции устанавливать «амплитуду» этого электрона в таком-то месте, в такую-то дату.
Возражения шли и дальше. Для того, чтобы написать уравнение (1.1) предварительно надо иметь право дифференцировать u(t), для этого – в частности – время t должно быть неограниченно дробимым. Нужно иметь право работать с бесконечномалыми промежутками времени dt и измеряемой физической величины du. Возражали – убедительно при том – что такой неограниченной беспредельной дробимости нет и быть не может, потому что не может быть никогда.
Возражали с информационной точки зрения. Пожалуй, ярче всего эта разновидность возражений обрисована братьями Стругацкими:
«Меня там больше всего заинтересовало многотомное издание Книги Судеб. Книга Судеб печаталась петитом на тончайшей рисовой бумаге и содержала в хронологическом порядке, более или менее полные данные о 73 6I9 024 511 людях разумных. //... // Последним в последнем томе регулярного издания, вышедшем в прошлом году, числился Франсиско-Каэтано-Августин-Лусия-и-Мануэль-и-Хозефа-: Мигель-Лука-Карлос-Педро Тринидад. (»Род. I6 июля I49I г. н.э. ум. 17 июля I49I г. //...//») . Из выходных данных явствовало, что Книга Судеб выходит тиражом в 1 (один) экземпляр и этот последний том поднисан в печать еще во время полетов братьев Монгольфье. Видимо, для того, чтобы как-то удовлетворить потребности современников, издательство предприняло публикацию срочных нерегулярных випусков, в которых значились только годы рождения и годы смерти. В одном из таких выпусков я нашел и свое имя. Однако из-за спешки и эти выпуски закралась масса опечаток, и я с изумлением узнал, что умру в 1611.» [2]
И лишь после публикации этого произведения Стругациких математики вычислили сложности соответствующих алгоритмов и убедились, что братья еще черезчур завысили возможности Отдела Предсказаний и Пророчеств своего НИИЧАВО. Ибо алгоритмы решения задач Коши растут как t3, и 1400 года вычислители достигли бы в 2*IO11 году (это коли мир сотворен в -5000 году; в противном случае еще гораздо позднее).
Иные уходили в сторону от лапласовской постановки вопроса, отказываясь вообще от бесконечности и дифференцируемости, занимаясь лишь теорией конечных автоматов.
Наверное, я не исчерпал всех способов отвергнуть лапласовский детерминизм, да я не собирался их перечислять и описивать [3] . Им всем общо то, что они возражают против применимости математических методов к TOЙ ИЛИ ИНОЙ ОБЛАСТИ РАССМОТРЕНИЯ; чаще всего эта область рассмотрения и не фигурировала во времена Ньютона-Лапласа. Например неприменима математическая теория дифференциальных уравнений к дискретному миру (а мир, – добавляет возражающий, – безусловно дискретен), и т.д. Примечательно однако, до какой степени психологически невозможно отрешиться от привязанности к дифференциальным уравнениям. В упомянутой выше статье Зельдовича и Михайлова авторы обсуждают некоторые химические реакции, справедливо отмечают, что усредненные модели неприемлемы, потому что крайне важны единичные флуктуации. А за тем для описания этих самых ЕДИНИЧНЫХ РЕЗКИХ ОТКЛОНЕНИЙ OT НОРМАЛЬНОГО ХОДА ВЕЩЕЙ прибегают к ничтожесумняшемуся использованию аппарата линейных дифференциальных уравнений. Вопреки тому, что вся идеология математического оправдания таких уравнений основана на НОРМАЛЬНОМ ХОДЕ ВЕЩЕЙ при ОТСУТСТВИИ резких отклонений! И мы, ставя вопрос о допустимости использования дифференциальных уравнений, не будем входить ни в какие обсуждения областей применимости оных вне математики. Мы вникнем в них на почве самой математики. Тут мы укажем пробел, который в полной мере был установлен только в начале восьмидесятых годов нашего столетия.
3. «Не нуждался в гипотезе» не значит, будто опроверг гипотезу.
Итак, мы сосредоточимся на том, что называется «механика» или «механическое воззрение на физику» [4]. Будем без возражений допускать, что описание мира или его части как обозримого набора точечных масс («материальных точек», «точечных наблюдателей») – приемлемо. В какой мере обоснован тогда детерминизм дифференциальных уравнений?
Вернемся к (I.I). При t = t0 значение u задано во всякой точке (x,y,z) – таково «условие игры». Согласно представлению причинности («каузальные воззрения») значения u(t0, х, y, z) могут каузально воздействовать на состояния u при t > t0. Точно также могут действовать и значения u(t`, x, y, z) при t`< t0 ; их вклад учитывается через их значения вдату t = t0, ибо ни одно причинное воздействие из прошлого в будущее не минует настоящего.
Все эти воздействия описываются уравнением (1.1), так что детерминированность u(t) при t > t0 есть лишь вопрос математической техники. Поэтому утвердилась точка зрения: «Дифференциальные уравнения оказались подходящими средствами моделирования физических процессов. Причем, если условия задачи полностью определяли процесс, то можно было ОДНОЗНАЧНЫМ образом предсказать законы его протекания. (см. вышеуказанный ташкентский сборник, стр.145). На самом деле – все куда как не так просто!
Ведь движение по траектории
где t произвольная положительная константа, не было запрещенным в ньютоновой механике. «Начинаясь» в бесконечности в дату t = t0, оно с законченными скоростями и ускорениями входило в конечную область пространства и приходило бы вположение x =0 в дату t = t0 + t . Говоря по-просту, неведомо откуда взявшееся и никак не зарегистрированное на дату t = t0 воздействие каузально влияло бы на покоящуюся (x = 0) материальную точку. Комбинируя (3.I) и
мы математически безупречно описали бы ситуацию: наблюдатель, покоящийся в точке x = 0, помолился Богу в дату t = t0 -t . По все ускоряющейся траектории его мольба устремилась к Богу, достигла в t = t0 бесконечности, и в тот же миг Бог послал свою ответную волю с бесконечнобольшим импульсом, который, войдя в физический мир, стал перемещаться с соблюдением физических законов и все замедляясь, а в дату t = t0 + t воздействовал на жизнь нашего наблюдателя, переменив его судьбу и обойдя при этом все граничные условия для дифференциального уравнения (1.1) на дату t = t0. Поэтому, хотя Лаплас и «не нуждался в этой гипотезе», но ИСКЛЮЧИТЬ ее у него не имелось средств. А тем самым и весь его механический детерминизм был – УЖЕ ТОГДА БЫЛ, до возникновения перечисленных и других возражений – НЕОБОСНОВАННЫМ.
Смутно ощущая возможность такой неприятной ситуации, физики XIX века тяготели к КОНЕЧН0МУ ПРОСТРАНСТВУ, дабы этих неудобств на бесконечности не случалось. Не вдаваясь в разбор всех перипетий этой идеи компактности, сообщим, что в теории относительности, где скорость всякого воздействия конечна, с описанной трудностью справились; траектории (3.1-2) исключили из числа возможных. Точнее, не в самой теории относительности, а в возникшей на ее основе теории каузальной структуры пространства-времени, где дали точные дефиниции нятиям «область Коши-зависимости», «каузальная граница», «поверхность Коши начальных данных» и т.п. [5]. Но этим не отменяется тот исторический факт, что в весь XIX век применимость дифференциальных уравнений к этой тематике оставалась математически необоснованной. Разговоры о механическом или механистическом, детерминизме в ХVIII и XIX веках и всю первую половину века ХХ – были необоснованными. Более, при пространственновременных концепциях веков ХУШ-XIX их и НЕЛЬЗЯ БЫЛО БЫ ОБОСНОВАТЬ.
Прежде чем переходить к дальнейшему, рекомендуем осознать, сколь многое в мышлении людей ХVШ-ХХ веков зависело, опиралось, подсознательно восходило к представлению о детерминированности. Начиная со стремления свести всю физику к механике (чем занималась физика едва ли не до конца ХIХ века ) и кончая «железными законами исторической необходимости», которые тоже возникли по аналогии с необходимостью механической!
4. Гладкие траектории.
А «механической необходимости» не было и не могло бы быть, даже если бы каким-нибудь декретом и запретили бы перемещения вроде (3.I-2). Потому что необоснованностей в подходе посредством дифференциальных уравнений было больше, нежели обоснованностей. Вернемся к поверхности Коши t = t0, предполагая, что допустимо только близкодействие, что неограниченно больших скоростей передачи каузального воздействия не существует, что область t = t0 в пространстве (x, y, z) конечна, как, например, в большинстве моделей современной космологии. Так что беспокоиться о помехах со стороны «Божественного вмешательства» (3.1) не приходится. На чем основывается однозначность решения дифференциального уравнения (1.1)? На представлении, что во внутрь области t>t0 с поверхности t = t0 из области t < t0 или вообще откуда угодно в мире можно попасть только по траектории, трансверсальной к поверхности t = t0 (cм. рисунок 1). И обратно: с поверхности t = t0 , следуя законам причинности, попасть можно только вовнутрь области t > t0 . Можно пасть по такой гладкой траектории, что достаточно близко от t = t0 какие две траектории не пересекутся. Кабы они пересеклись, то нарушилась бы однозначность результата: что же было бы в точке пересечения? Переданное по одной линии или переданное по другой?! Словом, ведут себя эти траектории вблизи от t = t0 так же, как короткие отрезки параллельных прямых. Сдвигая-перенося на бесконечно малое dt по этим прямым, мы от u(t0) переходим к u(t0 + dt)и т.д. (То, что тут присутствуют бесконечномалые в бесконечнобольшом количестве -- это уже внутриматематический технический вопрос, с которым математика умеет справляться.)
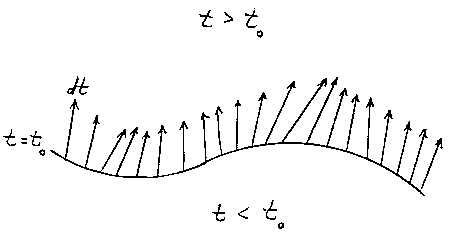
Если бы мы разрешали каузальному воздействию переноситься по каким угодно кривым, а не только по дифференцируемым (гладким), то ни за что не получили бы такой простой картины, ни за что не добились бы однозначности. Ведь нарушение гладкости при таком «бесконечно-большом увеличении», как на рисунке 1, где бесконечномалый dt показан конечной стрелкой, означало бы, что хоть одна из прямолинейных стрелок заменилась бы на ломаную, а та впилась бы в соседнюю прямолинейную стрелку, – и в месте их пересечения однозначность (детерминированность) нарушилась бы. Значит, НЕГЛАДКИЕ ТРАЕКТОРИИ ДОЛЖНЫ БЫТЬ ИСКЛЮЧЕНЫ. Именно это молчаливо подразумевалось со времен Ньютона-Лапласа. Поначалу и математики и физики исключали их per ignorantiae, просто не ведая о существовании негладких, недифференцируемых, неаналитических объектов. Со второй половины ХIХ века математики-то уже знали про наличие не дифференцируемых, даже нигде не дифференцируемых кривых, траекторий, функций, но физики еще не знали. Их это открытие не касалось – казалось им. Так что сложившуюся ситуацию вроде можно было бы описать такими словами: фактически для оправдания как парадигмы дифференциальних уралнений так и парадигмы детерминированности использовался НЕЯВНЫЙ ПОСТУЛАТ о выделенности гладких движений. Имплицитность, неявность постула та, конечно, со строго логической точки зрения – недостаток, но таких ПОДРАЗУМЕВАЕМЫХ постулатов в физике предостаточно, и из-за очевидной справедливости самого постулата «по существу» к серьезным недостаткам его неявность отнести нельзя. Так можно было бы думать. Увы, как мы увидим ниже, даже такая снисходительность не оправдана.
5 . Эмпирическая реабилитация математических монстров.
В семидесятые годы ХХ века Мандельброт выпустил книгу [6], где собрал богатый материал, убедительно вводивший в практический оборот многие из казавшихся безнадежно «абстрактными», «заумными», «патологическими» математических конструктов. И канторовы дисконтинуумы, и покрывающая всю плоскость кривая Пеано, и ковры-кривые Коха и Серьпиньского выглядят теперь как обнаруженные в реальности «главы» из «геометрии природы»; они помогли понять лунный пейзаж, скопления галактик и многое другое столь же невыдуманное, а глазам предлежащее.
Даже ДРОБНАЯ РАЗМЕРНОСТЪ (ну кому может присниться число измерений пространства, равное не целому числу! А математики «загодя» и такое ввели) по Хаусдорфу и Безиковичу – и та эмпирически сгодилась для измерения столь важного земного объекта, как дллина береговой линии побережья, изрезанного бухточками и подверженного приливам и отливам. Вопреки интуитивному убеждению, будто кривая линия всегда имеет размерность единица, линия британского побережья точнее вычисляется, если приписать ей размерность полтора. Нигде не дифференцируемая кривая Вейерштрасса пригодилась для описания броунова движения и качки корабля, т.е. его остойчивости. И, наконец триумфально вошли и научный оборот так называемые «странные аттракторы». Этот термин относится к полуэмпирически составленным метеорологическим уравнениям для течения неоднородно нагретого неоднородного газа, которые при их численном решении на компьютерах вдруг стали выдавать такие рисунки для распределения как бы притягивающихся один к другому слоев («аттракторы»), которые выглядели в точности как построение канторова дисконтинуума – заумнейшей модели, которая одно время и математикам-то казалась ненужной. [7]
В нашей цепочке рассуждений не так важно, когда и кто стал рассматривать подобные функции и множества в математике; упомянем лишь, что в России сильно-разрывные функции изучались еще Бугаевым, Крыловым, Лузиным, Флоренским на переломе ХIХ и ХХ веков. Нам здесь важно то обстоятельство, что эти объекты стали обнаруживаться КАК ПРИСУТСТВУЮЩИЕ В ПРИРОДЕ, а не как чисто УМОЗРИТЕЛЬНЫЕ конструкции. С математической точки зрения здесь самое существенное – НАЛИЧИЕ НЕПРЕРЫВНОСТИ ПРИ ОТСУТСТВИИ ГЛАДКОСТИ. Вот один вопиющий пример.
Кантором построена функция (которая называется то «чортовой лестницей», то «канторовой лестницей» в зависимости от того, пропускает ли редактор слово «чорт» или же он ханжа) с такими странными свойствами: она непрерывна на интервале, она почти везде на интервале имеет производную, всюду в точках существования производной производная равна нулю, но функция эта не постоянная, а монотонно возрастает на данном интервале, так что на концах любого интервала ее значения различны. Итак, из df = 0 не следует f = const. Значит, материальная точка в ньютоновой механике могла бы двигаться по такому закону: всюду, где она имеет мгновенную скорость, эта скорость равна нулю. Частица эта обладает мгновенной скоростью почти везде; это означает, что вероятность того, что в данный момент времени она имеет мгновенную скорость, – всегда равна единице. И тем не менее частица НЕ ПОКОИТСЯ на месте, но перемещается. Неуклонно в одном и том же направлении, поступательно, по прямой. Разумеется, это возможно исключительно за счет недифференцируемости траектории, хотя бы и на множестве меры нуль. Отметим еще, что и структура пространствавремени весьма существенна: такое возможно лишь при существовании сколь угодно быстрого перемещения (впрочем, не бесконечно быстрого); в условиях же ограниченности скоростей скоростью света изложенный парадокс невозможен. Но вот другое применение той же чортовой лестницы допустимо и к ньютоновой и к релятивистской механике. Возможно, что у материальной точки всегда d2x/dt2 = 0 там, где d2x/dt2 = 0 существует, а d2x/dt2 = 0 существует почти везде (т.е. существует с вероятностью вдиница). При этом dx(0)/dt = 0, x(0) = 0. но движение этой точечной массы происходит не по известным инерциальным законам x(t) = 0, но с ПЕРЕМЕННОЙ скоростью, с ПЕРЕМЕННЫМИ импульсами [8]. А ведь уравнение d2x/dt2 = 0 вроде бы «ручается» за отсутствие внешних сил! Другие примеры см. [9].
Вот эмпирика потребовала смотреть на кривые такого рода не как на математические ухищрения, которые применяются исключительно ради того, чтобы удобнее решить задачу, но кои из результата решения выпадают. Таким промежуточным образом в прикладной математике встречались недифференцируемые кривые в теории управления (задача о подъеме на гору, задача о движении, парусника против ветра). Нет, со времени введения фракталей в обиход науки о природе пришлось смотреть на такого рода кривые как на РЕЗУЛЬТАТ решения. Как на результат, которий воплощается в чем-то реальном. Например, эту самую чортову лестницу пришлось использовать не для описания вышеуказанной гипотетической частицы (т.е. контрпримера в определенных теоретических рассуждениях), а для изображения резонанса бесконечно многих источников, когда вычисления велись на компьютерах. Только она дала согласованное с эмпирикой решение для очень большого числа источников (см. в предыдущей сноске статью Бака).
6. Позиция философии.
Итак, математика оттачивала свой аппарат и создавала «тератологические модели», т.е. «монстров», а эмпирика углядывала и коллекционировала монстров в наблюдаемом мире, причем, о, это извечное и наждый раз свеже-волнующее чувство совпадения! Экспонаты подпадали под математическую мерку. Отставала лишь философия, которая продолжала мычать на языке древних греков о «дискретном-непрерывном». Философия упорно называла «непрерывным» то, что на деле было ГЛАДКИМ. Упорно не замечала НЕПРЕРЫВНЫХ, НО НЕ ГЛАДКИХ МОДЕЛЕЙ, которые составляют суть математической тератологии и эмпирических фракталей. Философия была и осталась неготовой к концептуальному обсуждению (не толкуя уж про ОПЕРЖАЮЩЕЕ обсуждение) этого материала. Распространенная в философии точка зрения заключается в том, что «дискретное» – это мол категория, которой противостоит категория. «непрерывного». При таком взгляде некуда втиснуть «гладкость». Вот и одна из причин, почему проблемы гладкости-негладклсти и не обсуждались [10] . Заметим, что противопоставление ДИСКРЕТНОГО – НЕПРЕРЫВНОМУ неудачно еще и потому, что первое является свойством МНОЖЕСТВА, тогда как второе – свойством ОТОБРАЖЕНИЯ. Правильнее ДИСКРЕТНОМУ противоставлять СВЯЗНОЕ, а уж отображения-функции-морфизмы тогда будут непрерывными.
С нашей точки зрения надлежит говорить про ОДНУ КАТЕГОРИЮ. Условно и приблизительно назовем ее МЕРОЙ ПОСТЕПЕННОСТИ. Значениями этой категории служат на наш взгляд, позиции: ДИСКРЕТНОСТЬ постепенность отсутствует вовсе), НЕПРЕРЫВНОСТЬ-СВЯЗНОСТЬ (постепенность присутствует, но иногда довольно непростая), ГЛАДКОСТЪ-ДИФФЕРЕНЦИРУЕМОСТЬ (постепенность такая хорошая, что в бесконечно-малом можно говорить про линейность). Впрочем, это скорее терминологический вопрос, хотя и немаловажный, как всякий выбор удобной терминологии.
А не терминологическое, но принципиальное значение имеет тот факт, что все примеры, которые приводятся в философских статьях, учебниках или словарях для иллюстрации НЕПРЕРЫВНОСТИ (как противопоставляемой дискретности), на самом деле суть примеры ГЛАДКОСТИ. Вот, скажем, в Философском энциклопедическом словаре [11] дискретному как непрерывное противопоставлены ВОЛНОВЫЕ СВОЙСТВА. Но волна -- это же объект, описываемый ДИФФЕРЕНЦИАЛЬНЫМ уравнением, следовательно, ГЛАДКИЙ ОБЪЕКТ! Если всмотреться, то такое смешение понятий обнаружится буквально повсюду. На каком-то этапе развития знания то словоупотребление, при коем гладкое называлось непрерывным, был вполне допустимым, терпимым. Никакой серьезной путаницы возникнуть; из-за этой терминологической вольности не могло, а указания математиков, что мол непрерывный объект может оказаться и негладким, законно было относить к снобистским придиркам. Но в последние положение вещей кардинально переменилось. Это связано как с внутрематематическим развитием (см. следующую рубрику), так и с накопленным эмпирическим материалом. Образцы накопленного материала нуждаются в адэкватном наименовании, а простой бинарный подход сваливает в одну кучу предметы из разных и разнородних нагромождений. Философия в своей терминологии не имеет права далее игнорировать наличный теоретический и практический запас сведений, а должна усовершенствовать свой лексикон применительно к сложившейся ситуации.
7. Гладкость как независимый и неабсолютный объект.
Математика тем временем продолжала свой анализ понятийных конструктов, и дифференциальная топология установила, что гладкость является совершенно самостоятельным объектом, НЕ ВЫВОДИМЫМ и НЕ СВОДИМЫМ ни из, ни к другим конструкциям. Что такое «гладкость»? Если М – топологическое многообразие, а R – множество вещественных чисел, то CРЕДИ ВСЕХ непрерывных отображений из М в R выделяется (ТО СЕМЕЙСТВО F, которое удовлетворяет определенным аксиомами (условиям, дефинициям, свойствам). Вот это-то семейство F и называется гладкостью (или «семейством гладких функций «или дифференциальной структурой») .
Чаще всего в приложениях гладкость вводят через СИСТЕМЫ КООРДИНАТ, через «карты», «атлас». У точки р ? М имеется окрестность, в которой любые точки задаются четырьмя координатами (t, x, y, z). У другой точки q ? М имеется своя окрестность, в которой точки выражаются тоже четырьмя координатами (t`, x`,y`,z`). На пересечении окрестностей координаты (t,x,y,z) и (t`, x`, y`, z`) не обязаны СОВПАДАТЬ, но обязаны выражаться одни через другие посредством дифференцируемых функций
Любой, читавший книжки про теорию относительности сталкивался с такой процедурой. И даже не зная формально про «гладкость», он в этом пункте соприкасался именно с гладкостью, ибо семейство гладких функций определяется (при одном из способов определения) как раз через такие преобразования координат. И могут существовать совсем иные координаты, которые сами по себе ничем не хуже (и не хуже) уже введенных, но которые, однако, не выражаются через ранее введенные посредством ДИФФЕРЕНЦИРУЕМЫХ функций (7.I). Это и будут РАЗНЫЕ ГЛАДКОСТИ на одном и том же пространстве (многообразии).
Так выяснилось, что на одном и том же многообразии М можно задавать разные гладкости. Но это не пугало, потому что переход от одной гладкости F к другой F` был прост, сводился к линейным морфизмам. Поясним на простейшем примере. На одномерном многообразии, на вещественной прямой R можно рассматривать функции f(х) , т.е. f :R ® R при условии, что они дифференцируемы по х. Это будет одна гладкость. И можно взять w = x1/3 и изучать функции g(w), тоже g:R ®R, дифференцируемые по w. Это будет ДРУГАЯ гладкость, потому что последние функции очевидным образом не дифференцируемы по x в нуле и следовательно, не попадают и число первых функций (и наоборот). Но зато всегда существует диффеоморфизм w :R ®R, при котором вторые функции превращаются в первые w :g ®f = gw , а раз это диффеоморфизм, то производные вторых функций получаются из производных первых функций посредством ЛНЕЙНОГО ПРЕОБРАЗОВАНИЯ df = dgdw . Конечно, одномерное многообразие мало интересно, но так же в точности было и для двумерного и для трехмерного многообразий. Напишем, например, уравнение Лапласа
для потенциала u в одной гладкости, а затем перейдет к другой гладкости. Там возникнут совсем иные производные, но они выражаются через прежние посредством невырожденного линейного преобразования
Следовательно, с точностью до этих линейных морфизмов (или, как предпочитает говорить И.А.Акчурин, «морфизмов евклидовой плоскости») объект изучения у нас ОСТАЕТСЯ ПРЕЖНИМ. Конечно, требуются некоторые уточнения насчет законов преобразования, но они давным давно найдены, сделаны и известны в теории тензорных преобразований и ковариантного дифференцирования.
И вот внезапно обнаружилось, что в размерности четыре, ситуация совершенно иная. В той самой размерности, которая нужнее всего физике. Ибо физике нужна еще координата t сверх координат (x, y, z) без t вообще о детерминации и говорить нелепо. Прежде всего, оказалось, что существуют такие 4-многообразия, на которых НЕЛЬЗЯ ВВЕСТИ НИКАКОЙ ГЛАДКОСТИ. Ну, досадно, но, может быть, именно эти многообразия и не так уж нужны? Может, и без них сумеет физика oбойтись? В конце-концов, самое распространенное в физике многообразие -- это R4 , т.е. по-просту то, что описывается системой координат (t, x, y, z).
Следующее по распространенности – это R* S3, так устроены почти все космологические модели. Неужели же НА НИХ мыслимы какие-либо пакости с гладкостью?! Увы. Обнаружено, что на R4 существует несколько (собственно, бесконечное число, счетное или несчетное – пока неясно) различных гладкостей, причем они – в отличие от двумерного и трехмерного случаев – НЕ БУДУТ ДИФФЕОМОРФНЫ. Значит, дифференциалы функций не будут получаться оцин из другого посредством линейных отображений. Значит, описания, выполненные посрецстлом дифференциальных уравнений, не будут изоморфными в разных гладкостях. То же самое с небольшими разночтениями относится к пространству R* S3 . Факт этот – факт математической теорематики. Он не зависит от эмпирических свойств мира, т.е. той реальности, к которой мы применяем математическое описание. Всегда, когда мы пишем дифференциальные уравнения для размерности выше третьей, ВСЕГДА выступает факт. РЕЛЯТИВНОСТИ ГЛАДКОСТИ. В низших размерностях гладкость была АБСОЛЮТНОЙ. Она существовала и была единственной – с точностью до обрисованных ваше линейных автоморфизмов над производными и дифференциалами. К этому привыкли и прежде ко всякой гладкости относились как к абсолютной. Теперь даже в тех случаях, когда гладкость существует, она НЕ ЕДИНСТВЕННА – для размерностей, начиная с 4, хотя в определенном смысле для размерностей 5 и 6 ситуация проще, нежели для 4. Объекты для разных гладкостей устроены существенно по-иному, они не изоморфны, значит, надо уметь ВЫБИРАТЬ СРЕДИ ЭТИХ ОБЪЕКТОВ. А мы не умеем. Нам не было нужды прежде проводить такой выбор и мы не научились. Может быть, мы научимся справляться с релятивностью гладкости. Не знаю. Я ведь пишу не о будущем, а о прошлом и о настоящем. В настоящем мы не умеем, в прошлом мы и не подозревали, что должны уметь.
8. Необоснованность механического детерминизма.
А это означает, что все, что писалось о детерминизме в XVIII-XX веках, НАДО ЗАЧЕРКНУТЬ. Ведь если у нас нт критерия «абсолютно различить» гладкую траекторию от негладкой на рис.1, то спрашивается, по каким же траекториям переносится «настоящее» физическое воздействие? Вот мы выбрали класс кривых, который в некоторой гладкости будет классом гладких кривых; постулируем, что каузальность распространяется по ним. Но чем ЭТА гладкость в наш век демографического равноправия в....... гладкостей лучше другой? А в другой эти же самые кривые (ибо выбор кривых никак не зависит от выбора гладкости!) уже будут НЕГЛАДКИМИ. Следовательно, приходится допустить, что каузальное воздействие и по негладким кривым может переноситься!.. А ежели оно может переноситься и по негладким кривым, то (как выяснилось в той же рубрике 4) тогда будет нарушаться каузальная однозначность, т.е. нарушаться детерминированность. И, как писалось в рубрике 5, при допущении не дифференцируемых кривых возникают очень странные механические объекты.
Вся идеология использования дифференциальных уравнений для детерминации будущего на основе настоящего и прошлого – рушится из-за релятивизации гладкости. И от того, что факт сей математиками открыли лишь к концу XX века, ничуть не легче при осмыслении концепции механического детерминизма и парадигмы дифференциальных уравнений, которые бытовали в XVIII, XIX и первых 3/4 столетия XX. Ведь и тогда эта лакуна в обосновании присутствовала – хотя бы и незримо. Детерминизм не был «Обнаружен в природе». Детерминизм не был «выведен логически» или «доказан математически». Мы всего лишь ВЕРИЛИ В ДЕТЕРМИНИЗМ. И в качестве веры, принимаемой за факт, он входил в парадигму механического (и шире) мышления.
9. Анизотропность и нарушения детерминации.
В изложении мы сосредоточили свое внимание на идее гладкости, на факте ее релятивности. На самом деле, причины, по которым требование гладкости делается неудобно-ограничительным, гораздо шире. Не перечисляя всех их, укажем только на потребности, связанные с построением теории анизотропного пространства-времени. Еще В.И.Вернадский настаивал [12], что пространство-время – АНИЗОТРОПНО. Что модели специальной и общей теории относительности, будучи в принципе изотропными [13], – НЕДОСТАТОЧНЫ. Так зрела проблема построения анизотропного обобщения теории относительности. Проблема построения такой теории, в которой скорость придельного сигнала (светового, электромагнитного) ограничена, но различна по разным направлениям (анизотропная среда). Такая теория построена [14]. И в ходе ее построения выявилась неизбежность перехода от привычных гладких функций – к функциям более широкого класса. Именно, с морфизмами упорядоченных множеств (а анизотропная финслерова теория относится «в бурбакистских терминах» к категории упорядоченных множеств) естественнее связаны не дифференцируемые, не аналитические, а ПОЧТИ ВЕЗДЕ ДИФФЕРЕНЦИРУЕМЫЕ функции. К этому классу, в частности, относится чортова лестница и созданные на ее основе странные частицы, а также дикие частицы из нашей книги 1968 года. [15]
Далее, однозначность, детерминированность решения многих дифференциальных уравнений (в частности для геодезических) связана (помимо обсуждаемых выше условий) с невырожденностью того, что называют «метрика», «метрический тензор», «лагранжиан».
Естественно, что если скорость. слета различна в разных направлениях, то фронт световой волны перестает быть сферическим. В частности, он может претерпеть уплощение, сделаться на каком-то участке ПЛОСКИМ. И как только он становится плоским, метрика сразу в направлении уплощения ВЫРОЖДАЕТСЯ, и по направлению к уплощению из одной точки выходит (при фикисированных начальных данных) не одна геодезическая, а бесконечно много их. Так еще раз – и по-новому – нарушается детерминация. В некоторых физических теориях, как отмечал А.Д.Сахаров [16], полезно использовать метрику переменной сигнатуры. При переходе же отодной сигнатуры к другой обязательно по непрерывности встретится точка вырождения метрики; следовательно, тут также нарушится каузальность в смысле детерминированности (это А.Д.Сахаров забыл отметить). При различной скорости света в разных направлениях у фронта световой волны могут возникнуть «углы» на стыках прямолинейных или криво линейных участков. Значит, в этой точке (точнее – в направлении на такой угол) дифференцируемость метрики нарушается,со всеми вытекающими отсюда и обговоренными ранее последствиями.
Исследования в этом направлении ведутся. Получены интересные результаты. Но преждевременно заявлять, будто эти исследования завершены. С точки зрения того «метапостулата гладкости» (мол допустимы к рассмотрению только гладкие структуры), о котором мы говорим, самым важным является такой силлогизм:
(А) Существенно-недифференцируемые структуры ВАЖНЫ в эмпирически-феноменологическом описании физической реальности;
(Б) Вся общая теория относительности (и базирующаяся на ней физическая космология) совместима ТОЛЬКО с очень хорошо дифференцируемыми структурами;
следовательно
НАДЛЕЖИТ построить такой аналог общей теории относительности, который был бы свободен от гипотезы дифференцируемости соответственно, от использования, дифференциальных уравнений.
Разумеется, при этом должен быть соблюден принцип перманентности, старая общая теория относительности должна вкладываться в новую теорию как определеный частный случай, а не отбрасываться.
Хотя – повторяем – многое сделано, но следы использования дифференциальных операторов еще очень сильны а в построенном финслеровом обобщении. А главное в ином. Построить такое обобщение – не значит выстроить математический каркас теории. Он должен быть наращен физическим «мясом», в него должна быть вдохнута философская душа.
10. Заключительные замечания.
Завершим статью схемой-диаграммой, иллюстрирующей место механической детерминированности в моделях описания (физической реальности:
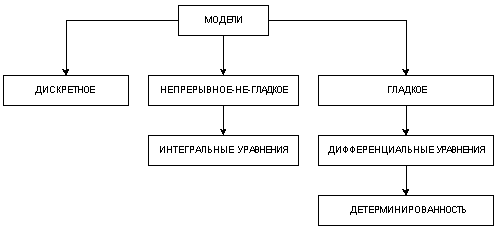
Предупредим одно возражение, недоразумение, которое может родиться нематематика, знакомого все же с достижениями современной физической космологии. В последней оживленно обсуждаются «сингулярности», исследуются те или иные «особые точки», где перестают быть применимыми методы дифференциальных уравнений. Может показаться, будто бы это и есть те самые «негладкие модели», о которых мы пишем. Нет. Дело в том, что вce встречающиеся в нынешней физической космологии особенности нарушения регулярности НУЖДАЮТСЯ для своей формулировки в ПРЕДВАРИТЕЛЬНОЙ возможности говорить о дифференциальной структуре. Это особенности в УЖЕ СУЩЕСТВУЮЩЕЙ ГЛАДКОСТИ. Нынешняя космология может (при усилии) справиться с КОНЕЧНЫМ числом особых точек, тогда как нарождающаяся концепция (соотносимая в диаграмме со средним членом «непрерывыое-не-гладкое») серее склонна к моделям, где особых точек бесконечно много и где они распределены всюду плотно, т.е. НЕУСТРАНИМО. Прибегнув к несколько легкомысленному сравнению, скажем так: упоминание в современной космологии сингулярностей подобно выезду горожан-туристов на лоно природы, максимум с одной-двумя ночевками и с прихваченными собою дарами города. А теория «непрерывного-не-гладкого» подобна безвыездной жизни в тайге от рождения. Этой теории будут чужеродны такие стандартные понятия современной космологии (и не только космологии), как «дифференцируемая кривая», как «касательная», как «производная», как «дифференциальное уравнение», как «ковариантное дифференцирование», как «дифференцирование по Ли», как «группа Ли», как «аффинная связность», как «дифференцируемое многообразие», как «тензор кривизны», как «поля Киплинга», как почти вce общеупотребительные «группы симметрий», как ... много еще чего удобного.
Ну, в утешение. Хотя при включении в рассмотрение непрерывных не-гладких структур парадигма ДИФФЕРЕНЦИАЛЬНЫХ уравнений ломается, все же сохраняется неизменной парадигма ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ, поскольку особенности на множестве меры нуль (особенности с нулевой вероятностью их проявления) погашаются при интегрировании . Это и показано на схеме.
Пименов Р.И. Дифференциальные уравнения – насколько они оправданы // «Академия Тринитаризма», М.,Эл № 77-6567, публ.11247, 31.05.2004
[Обсуждение на форуме «Публицистика»]
Дифференциальные уравнения – насколько они оправданы
1. Постановка вопроса.
2. Обходы проблемы.
3. «Не нуждался в гипотезе» не значит, будто опроверг гипотезу.
| х =-1/t +1/(t-t0), | ( 3.1) |
| х =-1/t -1/(t-t0), | (3.2) |
4. Гладкие траектории.

Рис. 1
5 . Эмпирическая реабилитация математических монстров.
6. Позиция философии.
7. Гладкость как независимый и неабсолютный объект.
Чаще всего в приложениях гладкость вводят через СИСТЕМЫ КООРДИНАТ, через «карты», «атлас». У точки р ? М имеется окрестность, в которой любые точки задаются четырьмя координатами (t, x, y, z). У другой точки q ? М имеется своя окрестность, в которой точки выражаются тоже четырьмя координатами (t`, x`,y`,z`). На пересечении окрестностей координаты (t,x,y,z) и (t`, x`, y`, z`) не обязаны СОВПАДАТЬ, но обязаны выражаться одни через другие посредством дифференцируемых функций
| t` = f1(t,x,y,z); x` = f2(t, x, y, z); y` = f3(t, x, y, z); z` = f4(t, x, y, z) |
(7.1) |
| d2u/dx2 + d2u/dx2 + d2u/dx2 = a | (7.2) |
| du/dx` = A11du/dx + A12du/dx+A13du/dx; du/dy` = A21du/dx + A22du/dx + A23du/dx; du/dz` = A31du/dx + A32du/dx + A33du/dx . |
(7.3) |
8. Необоснованность механического детерминизма.
Вся идеология использования дифференциальных уравнений для детерминации будущего на основе настоящего и прошлого – рушится из-за релятивизации гладкости. И от того, что факт сей математиками открыли лишь к концу XX века, ничуть не легче при осмыслении концепции механического детерминизма и парадигмы дифференциальных уравнений, которые бытовали в XVIII, XIX и первых 3/4 столетия XX. Ведь и тогда эта лакуна в обосновании присутствовала – хотя бы и незримо. Детерминизм не был «Обнаружен в природе». Детерминизм не был «выведен логически» или «доказан математически». Мы всего лишь ВЕРИЛИ В ДЕТЕРМИНИЗМ. И в качестве веры, принимаемой за факт, он входил в парадигму механического (и шире) мышления.
9. Анизотропность и нарушения детерминации.
10. Заключительные замечания.

11.05.88
г. Сыктывкар
Примечания Револьта Пименова.
г. Сыктывкар
Примечания Револьта Пименова.
- См. Акчурин И.А. Единство естественнонаучного знания. М.: Наука,1974; Зельдович Я.Б. и Михайлов А.С. Флуктуационная кинетика реакций /УФН, 1987, т.153, №З, -.469-486, Пригожин И. Самоорганизация в неравновесных систем М., Мир, 1979; Хакен Г. Синергетика М.: Мир, 1980.
- Стругациие А. и Б.Н. Понецельник начинается в субботу. М.,I965.
- На эту тему написано много. Из относительно свежих публикаций см. Принцип детерминизма в науках о природе и обществе. Ташкент: ТГУ, 1986.
- На самом деле практически так же рассматривают казуальность не только в механике, но и в теории поля (в макрофизике, например, и космологии). Но мы намеренно сужаем тему, дабы не вдаваться в третьестепенные подробности-различения.
- Пенроуз Р. Структура пространствавремени. М.: Мир, 1972.
- Mandelbrot B.B. Fractals. S-Francisco: Freeman, 1976. Falconer K.J. The geometry of fractal sets. Cambridge: University press, 1985.
- Соотнесенность фракталей именно с компьютерными вычислениями представляется мне одним из наиболее глубоких в своей таинственности фактом, но эта тема лежит за пределами сюжетов данной статьи.
- см. Пименов Р.И. Анизотропное финслерово обобщение теории относительности как структуры порядка. Сактывкар: КФАН, 1987.
- см. Пименов Р.И. Пространства кинематического типа. Л.: Наука, 1968 Bak P. When the interaktions .../ Physics today, 1986, N12, p.39-45. Hartmann F. Castiglano and Sobolev.// Singularities and constructive methods for their treatment. Proceenings. Oberwolfach 1983 Berlin, Springer, p.137-152.
- Она не главная, конечно. Более важные причины – общий застой в нашей философии. Безобразный порядок публикаций на философские темы: например, я посылал статью на эту тему в «Вопросы философии» еще в 1979 и, конечно, она не увидела света . См. Труды VIII международного конгресса по логике, философии и методологии науки, т.2, с.2I2-214.
- Философский энциклопедический словарь. М.: БСЭ, I983, стр.434.
- Вернадский В.И. Пространство время в неодушевленной и одушевленной природе. М., 1975.
- Применительно к общей тоеории относительности это утверждение раскрывается указанием на изотропность ее В БЕСКОНЕЧНОМ, т.е. касательном пространстве.
- См. Пименов, Анизотропное финслерово...Там же биография.
- См. Пименов, Пространства кинематического ...
- Сахаров А.Д. Космологические переходы с изменением сигнатуры метрики. //ЖЭТФ, 1984, т.198, N2, c.375-383.
Пименов Р.И. Дифференциальные уравнения – насколько они оправданы // «Академия Тринитаризма», М.,
|
|