|
|
|
В.Ю. Татур
Эта статья написана для тех, кто решил понять, что такое р-адические числа, как они представляются и вычисляются, почему их используют на расстояниях меньше планковских. Я попытался наиболее доходчиво, с примерами показать необычный мир р-адических чисел, чтобы это было понятно как тем, кто знаком с модулярной арифметикой, математическим анализом, так и тем, кто от этого далек – гуманитариям. Вместе с тем, в статье есть множество определений, что делает ее немного громоздкой, но позволяет увидеть логику создания и применения р-адических чисел. Возможно, что после ознакомления с представленным материалом кто-то посчитает необходимым изучить р-адические числа и анализ более глубоко.
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ
Десятичная система
Двоичная система
Примеры представления
Пример для дробных чисел
Троичная система счисления
Перевод из троичной системы в десятичную
Количество чисел в зависимости от основания
ДЕЛЕНИЕ С ОСТАТКОМ
СРАВНЕНИЕ ПО МОДУЛЮ
Свойства сравнения
КЛАССЫ ВЫЧЕТОВ ПО МОДУЛЮ
Остатки от деления
НЕКОТОРЫЕ ПОНЯТИЯ ОБЩЕЙ АЛГЕБРЫ
Поле
Абсолютная величина
Нормированное поле. Метрика, или расстояние
Р-АДИЧЕСКИЕ ЧИСЛА
Теорема Островского
Р-адический порядок и р-адическая норма
Канонические определения р-адического числа
Алгоритм нахождения р-адических чисел
Примеры определение р-адического порядка
Отрицательные р-адические числа
Извлечение корней
Древовидная структура р-адических чисел
Адельные числа
УЛЬТРАМЕТРИКА
МИР МЫШЛЕНИЯ
МИР ВЕЩЕСТВА
ПРОНИКНОВЕНИЕ МИРОВ
Р-адические числа и фрактальность
ВРЕМЯ
ПРЕДИСЛОВИЕ
Впервые я предложил использовать нестандартный анализ для описания биосферы в 1986 г. Эта идея вошла в доклад, прочитанный в том же году на одной из конференций и опубликованный в книге «Ноосфера и Человек» [1]. В том же 1986 году были подготовлены заметки к статье «Субстанция мысли и процесс эволюции». В ней я впервые выдвинул гипотезу, что мышление разворачивается на слабой метрике – особой форме материи, из которой возникают привычные нам пространство как протяженность и время как длительность. В этой статье я писал, что «человечество сейчас несознательно организует слабую метрику, вносит в нее огромные возмущения. Должно наступить время сознательной организации слабой метрики по ее законам и тем самым управление миром, процессами в нем. Каждой целостности соответствует свой образ в слабой метрике как целого, неделимый на элементы - идеал. К нему стремится система. У человека, как целостной системы, тоже есть идеал, но он связан с идеалом биосферы и ему подчинен. Идеал человека - определенное его состояние - состояние благого творчества.»
Здесь еще нет четкого понимания, что математикой слабой метрики является нестандартный анализ, возможность использования таких понятий как бесконечно малое гипердействительное число ε, т.е. монады Лейбница еще не стали элементами слабой метрики. Математическую монадологию в виде «нестандартного анализа» вернул к жизни в 1960 г. американский математик Абрахам Робинсон. Он доказал, что поле вещественных чисел может быть расширено до множества, содержащего бесконечно малые и бесконечно большие величины в том смысле, какой вкладывали в эти понятия Лейбниц и другие математики XVIII века, т.е. воскресил идею о существовании бесконечно малых величин, отличных от нуля. В созданном им «нестандартном анализе» бесконечно малые - не переменные величины, а особый вид чисел. В XVIII веке идея отличных от нуля бесконечно малых величин в математическом анализе усилиями Ньютона и его последователей была заменена понятием предела переменной величины.
Впервые предложение об использовании нестандартного анализа для описаний процессов в слабой метрике было доложено на конференции «Ноосфера – настоящее и будущее Человечества» и опубликовано в ее материалах в 1988 г. [2,3]. Однако представленные статьи были значительно ужаты до объема тезисов и упрощены, поэтому позднее они были в первоначальной версии опубликованы в книге «Ноосфера и Человек» [1].
А вот р-адическое разложение применительно к процессам, происходящим на уровне слабой метрики, я впервые попытался применить в 1990 г. [4] для описания раскрытия взаимодействия монады и галактики ε⊗D в слабой метрики и образования группы состояний двух пространств, представляющих 3-х мерную пространственно-подобную протяженность и 3-х мерную времени-подобную протяженность, что сопрягалось с идеями Роберто Орос ди Бартини о 6-ти мерном многообразии и естественной кинематической LT системе.
Идея применения р-адического разложения восходила к работам В.С. Владимирова и И.В. Воловича [5- 7], в которых они предположили, что р-адические числа могут быть использованы для описания пространства на расстояниях меньше планковского, поскольку согласно квантовой механики и представлениям о гравитации невозможно измерить расстояния меньше планковского, которое задается формулой lpl = √(ħG/c3) ≈1,616 229(38)·10−35 м, где ħ (h/2π) - постоянная Планка, с – скорость света и G - гравитационная постоянная.
Они предположили, что в пространстве с размерами меньше планковских не применим архимедов анализ, в частности, одна из аксиом евклидовой геометрии – аксиома измеримости, или аксиома Архимеда, которую можно сформулировать следующим образом.
Пусть есть прямая линия. Выберем на ней два отрезка а и b с началом в одной точке, причем а <b. Аксиома Архимеда гласит, что, прикладывая меньший отрезок а вдоль прямой ограниченное число раз, мы, в конце концов, превзойдем больший отрезок b. То есть для данного отрезка B длины b и другого (меньшего) отрезка A длины a, a< b, можно указать такое натуральное число n, что n • a > b.
Это означает, что геометрически мы должны иметь возможность измерить сколь угодно малые расстояния. Однако, в виду физического ограничения в виде планковской длины в реальном физическом пространстве это невозможно. Таким образом, мы приходим к выводу, что геометрия риманова пространства неадекватно описывает свойства реального физического пространства на очень малых расстояниях.
Между геометрией и числовыми системами существует соответствие. Например, обычная евклидова геометрия описывается при помощи вещественных чисел, для множества R которых аксиома Архимеда формулируется следующим образом: для любых двух положительных вещественных чисел l и L можно найти такое натуральное число n, что имеет место неравенство (n-1)l ≤ L < nl.
Возникает вопрос: если использование евклидовой геометрии для описания малых расстояний в физическом пространстве не подходит, то какую числовую систему вместо вещественных чисел мы должны использовать?
Для того чтобы ответить на него, представим себе результат физического эксперимента. Это – конечное число, которое можно записать в виде рационального числа. В научных экспериментах мы никогда не имеем дела, например, с бесконечными десятичными дробями, т.е. с иррациональными вещественными числами. При этом трудно себе представить, что когда-то будет такая точность измерений, которая позволит получить бесконечное количество знаком после запятой, т.е. интерпретировать результат, как вещественное число.
В.С. Владимировым и И.В. Воловичем впервые было подчеркнуто, что лишь рациональные числа являются физическими числами. Поэтому для описания физического мира отправной точкой следует брать поле рациональных чисел Q, т.е. алгебру, для элементов которой определены операции сложения, вычитания, умножения и деления (кроме деления на нуль).
Если бы кого-то спросили, что можно назвать «расстоянием между двумя рациональными числами», то многие дали бы такой ответ: «расстоянием» между двумя числами следует назвать модуль их разности. Такое определение вполне разумно, поскольку такое «расстояние» удовлетворяет всем аксиомам расстояния. Но, оказывается, расстояние между рациональными числами, удовлетворяющее всем аксиомам, можно ввести и по-другому. Это сделал немецкий математик Курт Вильгельм Себастьян Гензель (1861——1941). Он придумал даже целый класс таких расстояний – топологические пространства р-адических чисел. Эти числа были введены им в 1888 г., однако попытка опубликовать статью о них привела к конфликту с известным немецким математиком, внёсший существенный вклад в математический анализ и теорию чисел, Дирихле, который в течение почти 10 лет задерживал публикацию статьи, которая увидела свет только в 1897 г.[8]
О р-адических числах, р-адической норме, расстояниях ей соответствующим и мире, в котором мышление и физические процессы неразрывны, и рассказывается в этой статье.
ВВЕДЕНИЕ
Для того чтобы дать формулировку р-адическим числам, сначала сделаем небольшой экскурс в мо́дульную или модуля́рную арифметику.
Обозначения:
N – множество натуральных чисел n: 1,2, 3….,
N0 - множество натуральных чисел с 0.
Z – множество целых чисел – это N0 и отрицательные целые чисел вида (- n)
Q – множество рациональных чисел, представляемых обыкновенной дробью m/n, числитель m — целое число, а знаменатель n — натуральное число. Очевидно, что множество Q включает в себя Z.
R - множество действительных (вещественных) чисел. Вещественное число является целым, если его запись не содержит дробной части. Оно включает рациональные и иррациональные числа.
R\Q - множество иррациональных чисел. Это вещественные числа, не являющиеся рациональными. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Отрицательные и нецелые (рациональные, вещественные, …) числа к натуральным не относятся.
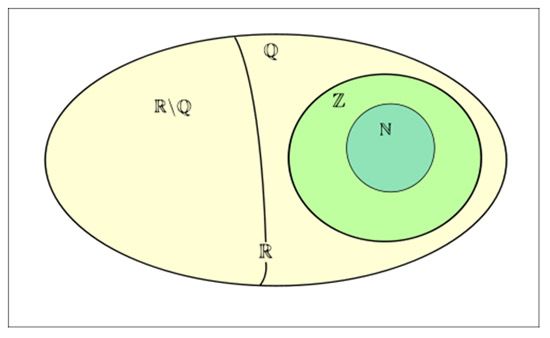
Рис.1
Начнем с представления чисел.
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ
Представление чисел (системы счисления) - символический метод записи чисел с помощью письменных знаков.
Рассмотрим позиционные системы счисления.
Под позиционной системой счисления обычно понимается b-ичная система счисления, которая определяется целым числом b>0, называемым основанием системы счисления. Целое число без знака x в b-ичной системе счисления представляется в виде конечной линейной комбинации степеней числа b:
x= Σak•bk, где k [0, n-1], ak — это целые числа, называемые цифрами, удовлетворяющие неравенству 0≤ ak ≤ (b-1).
Каждый базисный элемент bk в таком представлении называется разрядом (позицией). Каждая степень bk в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя k (номером разряда).
Число x записывают в виде последовательности его b-ичных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
x= an-1 an-2….a0
Например, число сто пять представляется в десятичной системе счисления в виде:
105 = 1•102 + 0•101 +5•100
или
1327 = 1•103+ 3•102 + 2•101 +7•100
Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 510, оно же в двоичной записывается как 1012.
Чтобы отличить от записи р-адических чисел, будем указатель в представлении действительных чисел подчеркивать: 510
12910 — это число 129 в десятичной системе счисления;
112103 — то же число 129 в троичной системе счисления;
100000012 — то же число 129, но в двоичной системе счисления;
Рассмотрим три системы счисления: десятичную, двоичную и троичную.
Десятичная система
Любое положительное действительное число х может быть записано в виде десятичной дроби:
х = ….+ a-k• 10-k +…. a-1•10-1 +a0•100 + a1•101 +…. + an•10n = an….a0, a-1…a-k…
где ak могут принимать только десять значений: 0,1,2….9., а первая цифра an означает первый не нулевой коэффициент при максимальном разряде
Число цифр справа после запятой неограниченно.
Двоичная система
Для двоичной системы b=2, тогда
x= (an-1 an-2….a0 )2=Σak•2k
n – количество цифр (знаков) в числе
ak – цифры из множества {0,1}, поскольку b -1 = 1
k - порядковый номер цифры, [0, n-1],
Дробное число, записываемое в двоичной системе счисления как an-1 an-2….a0, a-1 a-2… a-(m-1)a-m , имеет величину
x = (an-1 an-2….a0, a-1 a-2… a-(m-1)a-m )2 = Σak•2k
m – количество цифр дробной части числа
ak – цифры из множества {0,1}
k - порядковый номер цифры, [-m, n-1],
Количество цифр n – количество двоичных чисел, представляемых этими цифрами 2n-1
Поэтому
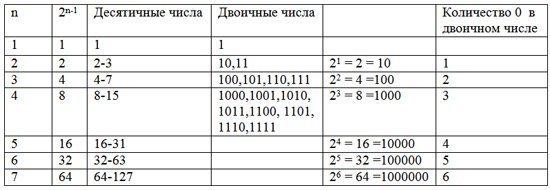
Примеры представления
Для числа x сначала берется максимальная степень k (разряд) числа 2 (основания) такое, что 2k≤ x < 2k+1
Например, разложение в ряд для десятичного числа 27 начинается с 24, поскольку 16(24)< 27< 32(25), а для числа десятичного 49 начинается с 25 , поскольку 32(25)< 49< 64(26),
После определения максимальной степени (разряда) число цифр в двоичном числе определяется как k+1. Столько же будет слагаемых в разложении этого числа.
Дальше идет определение коэффициентов перед 2k в порядке убывания степени (разряда) k так, чтобы в сумме получилось искомое десятичное число.
Тогда
27= 1*24 +1*23 +0*22 +1*21 +1*20
(27= 1*16 +1*8 +0*4 +1*2 +1*1)
или
2710 = 110112
49 = 1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20
(49 = 1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1)
4910=1100012
Можно предложить другой способ, как переводить в двоичную систему счисления десятичные числа. Возьмем то же число 49. Делим его на 2. Получается: 49/2=(остаток 1)24/2=(остаток 0)12/2= (остаток 0)6/2 = (остаток 0)3/2= (остаток 1)1. Затем следует выписать все цифры остатков:100011. Далее необходимо написать число наоборот (от последней цифре к первой). Получим 1100012.
Пример для дробных чисел
Нужно перевести число 1011011,0012 в десятичную систему.
1 * 26 + 0 * 25 + 1 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 + 0 * 2-1 + 0 * 2-2 + 1 * 2-3 = 91,125
Существует метод Горнера для перевода из двоичной в десятичную систему.
Например, двоичное число 10110112 переводится в десятичную систему так:
0*2 + 1 = 1
1*2 + 0 = 2
2*2 + 1 = 5
5*2 + 1 = 11
11*2 + 0 = 22
22*2 + 1 = 45
45*2 + 1 = 91
а дробное 0,0012
(0 + 1)/2 = 0,5
(0,5 + 0)/2 = 0,25
(0,25 + 0)/2 = 0,125
Троичная система счисления
В несимметричной троичной системе счисления чаще применяются цифры {0,1,2}, а в троичной симметричной системе счисления знаки {−,0,+}, {−1,0,+1}, {1,0,1} и т.д.
Примером представления чисел в несимметричной троичной системе счисления может служить запись в этой системе целых положительных чисел:
|
Десятичное число |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Троичное число |
0 |
1 |
2 |
10 |
11 |
12 |
20 |
21 |
22 |
100 |
101 |
Несимметричная троичная система счисления является частным случаем спаренных (комбинированных) показательных позиционных систем счисления, в которой ak — из троичного множества a={0,1,2}, b=3, веса разрядов равны 3k
Возьмем десятичное число 49.
Последовательность разложения по основанию 3 делается так же, как и по основанию 2, только цифры ak будут не из множества {0,1}, а из {0,1, 2}
4910 = 1 * 33 + 2 * 32 + 0 * 32 + 1 * 31 + 1 * 30 = 12113
Можно предложить другой способ, как переводить в троичную систему счисления десятичные числа. Возьмем то же число 49. Делим его на 3. Получается: 49/3=(остаток 1)16/3=(остаток 1)5/3= (остаток 2) 1. Затем следует выписать все цифры остатков:1121. Далее необходимо написать число наоборот (от последней цифре к первой). Получим 1211.
Перевод из троичной системы в десятичную
Для примера того, как счисление чисел в троичной системе можно вернуть к десятичной, используем число 20122. Для начала над каждой цифрой укажите её порядковый номер, начиная с 0: 24 03 12 21 20. Затем каждое число следует умножить на основание троичной системы, которое возводится в степень по номеру числа: 2*34+0*33+1*32+2*31+2*30. Полученные результаты суммируются (162+0+9+6+2). В результате будет число 179.
Количество чисел в зависимости от основания
Количество чисел, которые можно представить в зависимости от основания b при переходе от степени (разряда) k к k+1
Дается формулой N = (b-1)*bk
Например, при представлении десятичных чисел от 4 до 8 по основанию 2 k изменяется от 2 (4=22) до 3(8=23 ), тогда N = (2-1)* 22=4 (числа 4, 5, 6, 7). Если k=3, то количество чисел, представляемых по основанию 2 равно: (2-1)* 23=8 (числа 8,9, 10,11,12, 13, 14, 15)
При представлении десятичных чисел от 27 до 81 по основанию 3 k изменяется от 3 (27=33) до 4(81=34), тогда N = (3-1)* 33=54 (числа от 27 до 80).
При представлении десятичных чисел от 125 до 625 по основанию 5 k изменяется от 3 (125=53) до 4(625=54 ), тогда N = (5-1)* 53=500 ( числа от 125 до 624).
Таблица
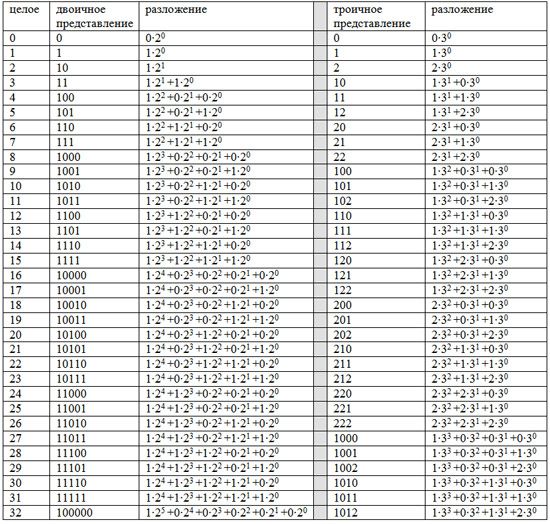
ДЕЛЕНИЕ С ОСТАТКОМ
Деление с остатком [9]— арифметическая операция, которую часто определяют для целых или натуральных чисел следующим образом. Пусть a и b— целые числа, причём b≠0. Деление с остатком a («делимого») на b («делитель») означает нахождение таких целых чисел q и r, что выполняется равенство:
a = b ⋅ q + r
Таким образом, результатами деления с остатком являются два целых числа: q называется неполным частным от деления, а r— остатком от деления. На остаток налагается дополнительное условие: 0 ⩽ r < | b | то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел. Если остаток равен нулю, говорят, что a нацело делится на b
Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка.
Операцию «взятия остатка» от деления a на b, обозначают mod: r = a mod b
Теперь обратимся к определению сравнения по модулю.
СРАВНЕНИЕ ПО МОДУЛЮ
Сравнение двух целых чисел по модулю натурального числа n — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на n один и тот же остаток.
Любое целое число может иметь не больше, чем n остатков; это значит, что все целые числа можно разделить на n групп относительно n, каждая из которых отвечает определённому остатку от деления на n.
Таким образом, говорят, что два целых числа a и b сравнимы по модулю натурального числа n, если при делении на n они дают одинаковые остатки.
Примеры:
14 и 20 сравнимы по модулю 6, так как 14=6•2 + 2, 20 = 6•3 + 2, или
32 и −10 сравнимы по модулю 7, так как 32 = 7•4 + 4, −10 = 7•(-2) + 4.
Утверждение «a и b сравнимы по модулю n» записывается в виде: a≡b (mod n)
Можно дать такие определения.
Определение 1. Целые числа а и b называются сравнимыми по модулю n, если их разность делится без остатка на n.
Например, 16 = 30 (mod 7), так как разность 16 — 30 = —14 делится на 7
Определение 2. Целые числа а и b называются сравнимыми по модулю n, если их остатки при делении на n одинаковы.
Таким образом, величина остатка может быть получена, как показано выше, бинарной операцией «взятия остатка» от деления a на b, обозначаемой mod:
r = a mod b, где 0 ⩽ r < | b |,
Это обозначение не следует путать с обозначением сравнения по модулю b. Формула для r влечёт выполнение сравнения:
r ≡ a (mod b)
Это сравнение не подразумевает выполнения неравенства 0 ⩽ r < | b | , необходимого для того, чтобы r было остатком.
Свойства сравнения
Приведу свойства функции сравнения:
1. Сравнения по одинаковому модулю можно почленно складывать: a1≡b1 (mod n), a2≡b2 (mod n) → a1+a2≡ (b1+ b2)(mod n),.
2. Слагаемое, стоящее в какой-либо части сравнения, можно переносить в другую часть, изменив его знак на обратный: a+b≡c(mod n) → a≡(c-b)(mod n).
3. К любой части сравнения можно прибавить любое число, кратное модулю: a≡b (mod n) → a+nk≡b (mod n).
4. Сравнения по одинаковому модулю можно почленно перемножать: a1≡b1 (mod n), a2≡b2 (mod n) → a1•a2≡(b2•b2)(mod n).
5. Обе части сравнения можно возвести в одну и ту же степень.
6. Как следствие из вышеперечисленных свойств, получаем:
a0≡b0 (mod n), a0≡b0 (mod n),….. am≡bm (mod n),
x≡y(mod n) → a0xm + a1xm-1 +…. am=( b0ym + b1ym-1 +…. bm ) (mod n)
7. Обе части сравнения можно разделить на их общий делитель, взаимно простой с модулем.
8. Обе части сравнения и его модуль можно умножить на одно и то же целое число или разделить на их общий делитель.
9. Если сравнение a≡b имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
10. Если сравнение имеет место по модулю n, то оно имеет место и по модулю d, равному любому делителю числа n.
11. Если одна часть сравнения и модуль делятся на некоторое число, то и другая часть сравнения должна делиться на то же число.
12. К обеим частям сравнения можно прибавить одно и тоже число; обе части сравнения можно умножить на одно и тоже число.
КЛАССЫ ВЫЧЕТОВ ПО МОДУЛЮ
Начнем с примера. Все числа, сравнимые с числом 2 по модулю 5, одинаково ведут себя при делении на 5 они дают остаток 2. Объединим эти числа в одно множество и назовем его классом вычетов по модулю 5. Обозначим этот класс той же цифрой 2, только, чтобы отличить его от числа 2 будем писать ее так: 2. Значит, 2—не число, а бесконечная совокупность чисел:
2 = {...-8, -3, 2, 7, 12, ...}
поскольку
-8 = (-2)•5+2
-3 = (-1)•5+2
2 = 5•0+2
7 = 5•1+2
12 = 5•2+2
Так же определяется класс вычетов по любому модулю n. При делении на n могут получиться n различных остатков: 0, 1, 2…. n— 1.
Например, при делении на 2
4/2 = 2+0
5/2 = 2+1
6/2 = 3+0
7/2 = 3+1
8/2 = 4+0
Имеем остатки 0 и 1, т.е. два остатка
При этом 4≡6≡8 (mod 2), а 5≡7 (mod 2)
При делении на 3
4/3 = 1+1
5/3 = 1+2
6/3 = 2+0
7/3 = 2+1
8/3 = 2+2
9/3 = 3+0
Имеем остатки 0,1,2, т.е. три остатка
При этом 4≡7 (mod 3), 5≡8 (mod 3), а 6≡9 (mod 3)
Таким образом, множество всех чисел, сравнимых с a по модулю n называется классом вычетов a по модулю n, и в этой статье обозначается an. Любое число класса называется вычетом по модулю n. Сравнение a≡b (mod n) равносильно равенству классов вычетов an = bn.
Остатки от деления
Каждому из остатков соответствует свой класс вычетов. Остатку r соответствует класс вычетов r, состоящий из чисел вида r+k•n, где k — целое число.
Возьмем модуль 3.
Для него остатки будут 0, 1, 2, поэтому будет 3 класса вычетов.
Начнем с остатка r=0
…
0+ (-2)•3 = -6
0+ (-1)•3 = -3
0+ (-0)•3 = 0
0+ (+1)•3 = 3
0+ (+2)•3 = 6
…
r=1
….
1+ (-2)•3 = -5
1+ (-1)•3 = -2
1+ (-0)•3 = 1
1+ (+1)•3 = 4
1+ (+2)•3 = 7
…
…
r=2
….
2+ (-2)•3 = -4
2+ (-1)•3 = -1
2+ (-0)•3 = 2
2+ (+1)•3 = 5
2+ (+2)•3 = 8
В пределах k=[-2,2] мы получили целые числа: -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8
Если бы был еще остаток r=3, то для него были бы следующие целые числа:
….
3+ (-2)•3 = -3
3+ (-1)•3 = 0
3+ (-0)•3 = 3
3+ (+1)•3 = 6
3+ (+2)•3 = 9
Мы видим повторение таких целых чисел как -3, 0, 3, 6.
Таким образом, все множество Ζ целых чисел распадается на n классов вычетов по модулю n. Множество всех классов вычетов по модулю n обозначается Zn (или Z/nZ): Zn = {0, 1,....., n — 1}. В приведенном примере Z3 ={0, 1, 2}.
Числа одного класса по модулю n имеют одинаковый Наибольший Общий Делитель (НОД).
НЕКОТОРЫЕ ПОНЯТИЯ ОБЩЕЙ АЛГЕБРЫ
Поле
Определение 3. Поле F – это множество с введёнными на нём алгебраическими операциями сложения + и умножения ∗(+F: FxF→F, *F: FxF→F т. е. для любого a,b ϵ F (a+b) ϵ F, a*b ϵ F), если выполнены следующие аксиомы:
1. Коммутативность сложения: для любых a,b ∈ F a+b=b+a.
2. Ассоциативность сложения: для любых a,b,c ∈ F (a+b)+c=a+(b+c)
3. Существование нулевого элемента: ∃0∈ F: для любого a ∈ F a+0=a.
4. Существование противоположного элемента: для любого a ∈ F ∃(-a)∈ F: a +(-a) =0
5. Коммутативность умножения: для любых a,b ∈ F a*b=b*a
6. Ассоциативность умножения: для любых a,b,c ∈ F (a*b)*c=a*(b*c)
7. Существование единичного элемента:∃e∈ F: для любого a ∈ F a*e=a.
8. Существование обратного элемента для ненулевых элементов: (для любого a ∈ F: a≠0) ∃a-1 ∈ F: a* a-1 =e
9. Дистрибутивность умножения относительно сложения: для любых a,b,c ∈ F (a+b)*c=(a*c)+(b*c)
Абсолютная величина
Определение 4. Абсолютная величина, или модуль числа a есть неотрицательное число, определение которого зависит от типа числа a. Обозначается как |a|.
В случае вещественного a абсолютная величина определяется следующим образом:
|a| = (a, если a≥0, –a, если a<0).
Область определения: ( − ∞ ; + ∞ ).
Область значений: [0,+∞) .
Абсолютная величина обладает следующими свойствами:
а) |a| > 0, причем |a| = 0 тогда и только тогда, когда a = 0;
б) |a· b| = |a| · |b|;
в) |a + b| ≤ |a| + |b|.
Нормированное поле. Метрика, или расстояние
Пусть F – поле, a,b ∈ F
Определение 5. Функция ||•||, определенная на R и принимающая значения в R≥0 (R+) называется нормой на F (также, абсолютной величиной, если упорядоченное поле является полем вещественных чисел), если она удовлетворяет следующим условиям:
(1) Для любого a ∈ R справедливо, что ||a|| = 0 тогда и только тогда, когда a = 0.
(2) Для каждой пары a, b ∈ R справедливо равенство ||a•b||= ||a||•||b||.
(3) Для каждой пары a, b ∈ R справедливо неравенство ||a + b|| ≤ ||a|| + ||b||.
С помощью нормы можно ввести метрику, индуцированную этой нормой. В этом случае поле F можно рассматривать как метрическое пространство.
Определение 6.
Пусть M — некоторое непустое множество, и пусть d: M х M → R≥0 (R+) — функция двух переменных, определенная на этом множестве и принимающая значения во множестве действительных неотрицательных чисел (R+) . Функция d называется метрикой, или расстоянием (а множество M— метрическим пространством), если d удовлетворяет трем условиям:
(1) Для каждой пары a, b ∈ M справедливо: d(a, b) = 0 тогда и только тогда, когда a = b.
(2) Для каждой пары a, b ∈ M справедливо равенство d(a, b) = d(b, a).
(3) Для каждой тройки a, b, c ∈ M справедливо неравенство d(a, b) ≤ d(a, c) + d(c, b).
Например, множество R всех действительных чисел есть метрическое пространство с метрикой d(a, b) = ||a−b|| = |a−b|, где ||•|| есть норма, а |•| есть абсолютная величина.
Р-АДИЧЕСКИЕ ЧИСЛА
Как я пояснял выше, физическими являются только рациональные числа Q, которым соответствует поле рациональных чисел. Геометрическому понятию расстояния соответствует аналитическое понятие нормы на Q, т.е. функции ||х|| со свойствами, данными в Определении 5
(1) ||х||≥0, причем ||х||=0 при х=0
(2) ||х•y|| = ||х||•||y||
(3) ||х+y||≤||х|| + ||y||
для любых рациональных чисел х, у.
Вещественной нормой рационального числа x называется его модуль |x|, т.е. ||x||=|x|. Вещественная норма рационального числа есть число рациональное. Полем вещественных (действительных) чисел называется пополнение поля рациональных чисел по вещественной норме, которая удовлетворяет условиям 1) -3).
Есть ли еще какие нормы на Q?
Теорема Островского
Нормы ||x|| и ||x||р , р =2,3,…исчерпывают все нетривиальные неэквивалентные нормы поля рациональных чисел Q.
Иначе говоря, любая норма на поле рациональных чисел Q эквивалентна либо вещественной норме (обычному абсолютному значению), либо одной из p–адических норм, где р- простое число.
Удивительно, что существует только два пополнения поля рациональных чисел: по вещественной и р-адической нормам. Мир смотрит на рациональные числа с помощью двух кардинально различных состояний.
Р-адический порядок, р-адическая норма и р-адическое расстояние
Р-адическая норма ||x||p определяется следующим образом.
Пусть p – простое число. Представим рациональное число х в виде x =pγ• (m/n), где m и n – целые числа, которые не делятся на р. Такое представление однозначно. Тогда
||x||p=p−γ
Таким образом, р –адическая норма измеряет, на какую степень p делится рациональное число, и норма тем меньше, чем больше эта степень, то есть последовательность {pγ}, γ→+∞, будет стремиться к нулю в p–адической норме.
В силу теоремы Островского других норм на Q нет. Нетрудно проверить наличие свойств 1) - 3) для ||x||p. Однако фактически вместо неравенства треугольника 3) имеем более сильное неравенство
3') ||х+y||≤ max( ||х||p, ||y||p)
Норма, которая удовлетворяет неравенству 3'), называется неархимедовой.
Пополнение поля рациональных чисел Q по обычной, вещественной норме приводит к полю вещественных чисел R, а пополнение по р-адической норме – к полю р-адических чисел Qp для любого простого р.
Итак, начнем с определения р-адического порядка.
Определение 7
Пусть р-простое число. Определим р-адический порядок γ=ordp(x) рационального числа x ∈ Q следующим образом
1) если x ∈ Z, то ordp(x) равен высшей степени р, которая является делителем x
2) если x = a/b, где a,b ∈ Z, то ordp(x) = ordp(a) - ordp(b)
3) положим ordp(0) = +∞
Для примера возьмем натуральное n ∈ N. Найти ordpn можно по следующему правилу: представим n в системе счисления с основанием p, найдем номер самого младшего ненулевого разряда в этом представлении (пусть это номер i, нумерация начинается с нуля); тогда ordpn = i.
Другими словами,
если nр =0…0ai ai+1….. (i нулей); ai ≠0, то ||n||p =p-i .
Например, 3-адическая запись числа 15=0•30+2•31+1•32
15= a0, …a2=0213, γ=ord3(15)=1
или 5-адическая запись числа 247
247= 2•50 + 4•51+ 4•52+1•53 =24415, γ=ord5(247)=0
или 2-адическая запись числа 100 = 0•20+0•21+1•22+0•23+0•24+1•25+1•26 = 00100112, γ=ord2(100)=2
Определение 8.
р – адической нормой рационального числа х, представленного единственным образом в виде несократимой дроби x =pγ(m/n), где p есть простое число, γ есть целое число, m целое, n натуральное, а p, m, n взаимно просты, называется число
||x||p=p−γ, если x≠0, и 0, если x=0.
р-адическое нормирования рациональных чисел является дискретным, т.е. норма может принимать лишь дискретное множество значений.
Для того чтобы норма ||•|| была неархимедовой, необходимо и достаточно, чтобы ||n|| ≤1 для любого n ∈ Z
Или такое определение р-адической нормы для множества целых р-адических чисел Zр
Определение 9. Если a ∈ Zр отлично от нуля, то его р-адической нормой называется число ||a||p = р-n, где n – наибольшее натуральное число n, для которого a делится на pn. Если a =0, полагают ||a||p = 0
Определение 10. р-адическим расстоянием между числами a,b ∈ Zр называется число ||a-b||p
Рассмотрим пример 2-адического расстояния
Пусть а и b — рациональные числа. Если а ≠ b, то представим число a-b в виде а-b = 2k •(m/n), где m и n — нечетные числа, a k—целое число (положительное, отрицательное или нуль). 2-адическим расстоянием между числами а и b, а ≠ b, называется число d(a, b) = 1/2k. Если а=b, то положим d(a, b) = 0.
Это расстояние измеряет степень делимости рационального числа на 2, т.е. чем лучше делится число на 2, тем ближе оно к нулю. Например, 8 ближе к нулю, чем 1/2, 16 ближе к нулю, чем 8, 480 ближе к нулю, чем 16, но дальше от нуля чем 384
Определение 11.
Полем Qp p–адических чисел называется пополнение поля Q рациональных чисел по p–адической норме.
Поля p –адических чисел Qp – единственный примеры неархимедовых числовых полей, получаемых пополнением поля рациональных чисел Q.
Поля, соответствующие различным простым числам, например Q2, Q7, Q1999 –не изоморфны, т.е. нельзя путем обратимых отображений перевести структуру одного поля в другую поскольку при этом не сохраняется структура полей. Более того, поля Qp p–адических чисел вообще не является упорядоченным множеством, в отличие от множества действительных чисел, т.е. мы не можем сравнить два произвольных р-адических числа.
Так же не изоморфно любому Qp поле действительных чисел R.
Поле p –адических чисел является важнейшим примером ультраметрических пространств, которые были введены в 1943 г. французским математиком Краснером. Ультраметричность является основой развития анализа над неархимедовыми числовыми полями. Наша геометрическая интуиция, развитая на евклидовой геометрии, оказывается бессильной для анализа ультраметрических пространств. Об этом я расскажу чуть ниже.
Канонические определения р-адического числа
Как было определено в разделе о представлении чисел, любое положительное действительное число х может быть записано в виде десятичной дроби:
x = ….+ a-k• 10-k +…. a-1•10-1 +a0•100 + a1•101 +…. + an•10n = an….a0, a-1…a-k…
где ak могут принимать только десять значений: 0,1,2….9.
В общем случае, если m >1 - любое фиксированное целое число, то любое положительное действительное число x может быть записано в виде:
x= ….+ a-k• m-k +…. a-1•m-1 +a0•m0 + a1•m1 +…. + an•mn = an….a0, a-1…a-k… (1)
где ak могут принимать 0,1,2….m-1, an≠0
Это разложение единственно, за исключением случая, когда все ak для достаточно больших k равны m-1.
Положительные целые числа могут быть записаны в базисе m как конечные суммы
x = a0•m0 + a1•m1 +…. + an•mn (2)
Любое р-адическое число (р-простое) х можно представить в виде суммы
x = a-f• p-f +…. a-1•p-1 +a0•p0 + a1•p1 +…. + an•pn +…. = a-f …… a-1,a0a-1…an …. (3)
или
x = an•pn + an+1•pn+1 + …..
где ai ∈{0,1….p-1}, n ∈ Z
При этом число х называется целым, если n≥ 0
По аналогии с записью вещественных чисел, для записи p-адических чисел вводится разделительная запятая (или точка), как средство задания знака показателя степени р в разложении числа в степенной ряд:
Для n < 0, х = an …. a-1, a0a1 …
Для n = 0, х = 0,an an+1 … (обычно 0 и запятую не пишут)
Для n> 0, х = 0,00an an+1 … где количество 0 после запятой равно n
Такой вид записи называется каноническим
Например, 3-адическая запись числа 15= 0•30+2•31+1•32=2•31+1•32, n = 1, количество 0 в записи – один: 15= 0,a0, …a2=0,0213=0213
Число (2) записывается в виде an….a0,0 в соответствии с вещественным представлением (1).
И то же самое число (2) записывается в виде 0, a0…an (если без разложения с нуля, то a0, …an ) в соответствии с р-адическим разложением (3).
Например, возьмем число 10 по основанию 2.
ak= {0,1}
1010 = a0•20 + a1•21 + a2•22 + a3•23 …. + an•2n
Тогда 1010 = 0•20 + 1•21 + 0•22 + 1•23
1010 = a3….a0 =10102
Тогда 2-адическое представления числа 1010 будет
1010= a0, …a3=01012
Или возьмем число 15 по основанию 3,
ak= {0,2}
1510 = a0•30 + a1•31 + a2•32 + a3•33 …. + an•3n
Тогда 15 = 0•30 + 2•31 + 1•32
1510 = a2….a0 =1203
Рассмотрим 3-адическое представления числа 1510
1510= a0, …a2=0213
Иногда р-адические числа записывают бесконечно влево, например для n = 0, х =…….. an+1 an ,0, чтобы таким образом, в некоторых случаях, не путать их с записями вещественных чисел. Например, в случает отрицательных чисел.
Возьмем число -1. Как элемент Z5 оно записывается иногда в виде …..4444,0, хотя каноническое представление -1 = 0,4444……5 При этом 5-ричное разложение 1 = 0,44444…5 Чтобы не возникало недоразумений, последнее разложение эквивалентно 1,(0)= 0,999999….10= 0,(9). Для 10-адичного представления -1 = 0,9999… 10= 0,(9) поэтому, чтобы отличить от канонического представления записывают как …….99999 = -1
При совпадении записи смысл ее различный. Если при каноническом р-адическом представлении чем дальше вправо от нуля, тем больше разряд, то при обычной записи действительного числа: чем дальше вправо от нуля, тем разряд меньше.
В дальнейшем будем различать каноническую р-адическую запись от другой значком +. Например, -110 = 0,4444……5 = …….4444,05+=, или 310= 1100…2 = …00112+
Р-адическое представление схоже с представлением действительного числа в виде дроби, но отличается от действительного случая неограниченностью в направлении возрастания степеней р и ограниченностью в направлении их убывания.
Любое действительное число является рациональным тогда, когда его р-адическое разложение является периодичным. Иначе говоря, р-адическое разложение числа a ∈ Qp периодично начиная с некоторого места тогда и только тогда, когда a ∈ Q. Если разложение не периодично ни с какого места, то ему не соответствуют ни рациональные, ни действительные, ни комплексные числа.
Например, . . . 1000010001001012+
Есть несколько определений р-адических чисел
Определение 12 (стандартное) [10]
Целым p-адическим числом для заданного простого p называется бесконечная последовательность {x1, x2,…} вычетов xn по модулю pn, удовлетворяющих условию:
xn≡xn+1 (mod pn)
Сравнение xn≡xn+1 (mod pn) равносильно равенству классов вычетов [a]n = [b]n
Беря в качестве элемента класса вычетов число хn такое, что 0 ≤ хn < pn, мы можем записать каждое целое p-адическое число в виде x =х1х2… хn… однозначным образом. Записывая каждое xn в p-ичной системе счисления xn=an…a2a1 и учитывая, что xn ≡ xn+1(mod pn), мы можем всякое p-адическое число в каноническом виде представить в виде последовательности x = a0, a1a0, a2a1a0,….. Действия над ними производятся по обыкновенными правилами сложения, вычитания и умножения «столбиком» в p-ичной системе счисления.
Метрическое построение
Любое рациональное число r = pγ•(m/n), где m и n целые числа, не делящиеся на p, а γ — целое. Тогда ||r||p — p-адическая норма r — определяется как p-γ. Если r=0, то ||r||p =0.
Как уже отмечалось выше, поле p-адических чисел есть пополнение поля рациональных чисел с метрикой dp, определённой p-адической нормой: dp (x,y) = ||x-y||p. Это построение аналогично построению поля вещественных чисел как пополнения поля рациональных чисел при помощи нормы, являющейся обычной абсолютной величиной.
Суммируя представленное выше можно дать определение р-адического числа
Определение 13
Любое р-адическое число x ∈ Qp, х≠0 однозначно представлено в каноническом виде
х= Σ dk•pk = pγΣ xj•pj = pγ • (x0•p0+x1•p1+x2•p2+ …)
γ ∈ Z, xi = di+ γ, xi=0,1,…p-1, xi ≠0, , k [γ, ∞), j [0, ∞),
dk – целые числа, 0 ≤ dn ≤ р-1, если d0 ≠0, то представление однозначно.
Такие ряды можно рассматривать как числа, записанные по основанию р, которые бесконечно продолжаются, например, влево, или содержат бесконечно много р-адических цифр перед запятой и лишь конечное число цифр после нее:
Например, x = …dk… d2 d1 d0 ,d-1 d-2… dγ
Или в каноническом виде
x = dγ… d-2 d-1 , d0 ,d1 d2… dk…
Поскольку р-адические числа, как было отмечено выше, находятся во взаимно однозначном соответствии со сходящимся в р-адической норме рядами вида
х = Σ di•рi, (4)
где γ – целое, γ≤ i<∞, di = 0,1, …р-1,
то возникает вопрос: что значит, что ряды сходятся в р-адической норме?
Это значит, что для любого ε> 0 можно выбрать такое N(ε), что р- N(ε) < ε, и для k >n> N(ε) будем иметь, например при γ = -m (отрицательное целое)
|Σ di•рii=[-m,k] - Σ di•рi i=[-m,n] |p = |Σ di•рi i=[n+1,k] | p ≤ max i=[n+1,k] |di•рi| p ≤ р- N(ε) < ε
Это говорит о том, что частичные суммы Sn = Σdiрii=[-m,n] ряда (4) образуют последовательность Коши по норме ||•||p.
Например, возьмем формулу для суммы бесконечной геометрической прогрессии
1+q+q2+q3+...+qn+...=1/(1- q), где любое di=1, q=р, γ =0
Тогда разница Sn = Σ qi i=[0,n] и Sn+1 = Σ qi i=[0,n+1] , будет qn+1
Откуда, || qn+1||q = q -(n+1)
Поскольку q - простое число, то при n →∞ q -(n+1) →0, то очевидно, что для любого ε> 0 всегда можно найти такое N(ε), что q- N(ε) < ε,
Иначе говоря, окрестность нуля за номером n состоит из всех чисел, которые делятся на qn и самого нуля. При этом, как полагается, окрестности с большим номером оказываются вложены в окрестности с меньшим номером.
Таким образом, каждый ряд представляет элемент поля Qp
Рассмотрим частный случай q=2.
Тогда 1/(1-2)=-1 = 1+2+22+23+...+2n+...=111111….2
Общий случай
-1 = (р-1)/(1-p) = (p-1)•1+(p-1)•p+(p-1)•p2+(p-1)•p3+...+(p-1)•pn+..
Приведу примеры.
По определению норм
||2||2=1/2, ||2||3= 1.
||6||3=||15||3=1/3, ||137||2= 1, ||1/4||2=||3/4||2=4
Почему?
р=2, тогда 0 ≤ dn ≤ 1
22=( … 0•2-1+ 0•20 + 1•21+ 0•22…) = 21• ( … 0•2-2+ 0•2-1+ 0•20 + 1•20+ 0•21…), γ =1, ||2||2= 2-γ =1/2
1/42= ( … 1•2-2+ 0•2-1+ 0•20 + 0•21…) = 2-2 ( … 1•20+ 0•21+ 0•22 + 0•23…), γ = -2, ||1/4||2= 2-γ =22=4
3/42= 2-2 ( … 1•20+ 1•21+ 0•22 + 0•23+ 0•23…)
1372= 20 ( … 0•2-2+ 0•2-1+ 1•20 + 0•21+ 0•20+ 1•23…+….1•26….)
р=3, тогда 0 ≤ dn ≤ 2
23= ( … 0•3-1+ 2•30 + 0•31+ 0•32…) = 30 ( … 0•3-1+ 2•30 + 0•31+ 0•32…), γ =0, ||2||3= 3-γ =1
63= ( … + 0•3-1 + 0•30+ 2•31+ 0•32…) = 31 ( … + 0•3-1+ 2•30 + 0•31+ 0•32…), γ =1, ||6||3= 3-γ =1/3
153= ( … + 0•3-1 + 0•30+ 2•31+ 1•32…) = 31 ( …+ 0•3-1 + 2•30+ 1•31+ 0•32…), γ =1, ||15||3= 3-γ =1/3
Вообще, какой алгоритм нахождения р-адических чисел, если использовать определения вычетов?
Алгоритм нахождения р-адических чисел
Покажем на двух примерах.
1. x=15 в 3-адическом базисе
ak= {0,1,2}
Определим а0
х1 ≡ 15(mod 31) =0 = a0•30 , a0 =0, х1= a0
х2 ≡ 15( mod 32)=6 (остаток от деления 15 на 9)= a0•30 + a1•31, a1 =2, х2= a0 a1
х3 ≡ 15 (mod 33)=15= a0•30 + a1•31+ a2•32, a2 =1. х2= a0 a1 a2
Тогда 1510=0213
Таким образом, максимальная степень i числа 3 связана с равенством нулю целой части при делении числа 15 на pi
Условие
xi ≡ xi+1 (mod pi)
выполняется для всех х. Так х2 ≡ х3 (mod 32) поскольку х3 – х2 = 1•32 и (х3 – х2 )mod 32 = 0 (остаток от деления 9 на 9)
2. a=247 в 5-адическом базисе
ak= {0,1,2,3,4}
х1 ≡ 247 (mod 51) =2 (2 остаток от деления 247 на 5, целое 45) = a0•50 , a0 =2
х2 ≡ 247 (mod 52) =22 (22 остаток от деления 247 на 25, целое 9) = a0•50 + a1•51, a1 =4
х3 ≡ 247 (mod 53) =122 (122 остаток от деления 247 на 125, целое 1) = a0•50 + a1•51+ a2•52, a2 =4
х4 ≡ 247 (mod 54) =247 (247 остаток от деления 247 на 625, целое 0) = a0•50 + a1•51+ a2•52+ a3•53, a3 =1
Тогда 24710=24415
Алгоритм может быть почти такой же только модифицированный тем, что каждый последующий коэффициент в разложении вычисляется следующим образом:
247/5 = 49 + (2/5), 2 (остаток от деления) = a0•50 , a0 =2
247 – 2= 245
245/25 = 9 + (20/25), 20(остаток от деления) = a1•51 , a1 =4
247 – 2 – 20 = 225
225/125 = 1+(100/125), 100(остаток от деления) = a2•52 , a2 =4
247 – 2 – 20 – 100 = 125
125/625 = 0 + (125/625), 125(остаток от деления) = a3•53 , a3 =1
Вместе с тем, 24710= 14425 = 1•53 + 4•52+ 4•51+ 2•50
Нетрудно заметить, что 5-адичная и 5-ичная форма записи рассматриваемого в качестве примера положительного целого числа х=247 совпадают с точностью до порядка слагаемых в частичных суммах степенного ряда. Однако, в 5-адичной записи ak записываются, начиная с младших разрядов, а в 5-ичной ak традиционно записываются, начиная со старших разрядов.
Примеры определение р-адического порядка
Например, найти ordpn, n ∈N можно по следующему правилу: представим n в системе счисления с основанием р, найдем номер самого младшего ненулевого разряда в этом представлении (пусть это номер i, нумерация начинается с нуля) тогда ordpn = i.
Другими словами,
Если n=00…0ai ai+1……, количество нулей равно i, ai ≠0, то ||n||p = p-i
Каноническое представление целого р-адического числа а
a = a0… ai-1ai…. = Σ aipi
где 0≤ i <∞
Как еще можно определить ordpn?
Представим в виде произведения простых чисел, например, число 102 = 21• 31• 50• 70• 110• 130• 171•190… (5)
(напомню простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113,…., т.е. те, которые делятся на себя и 1)
2-адическая запись числа 102 = 01100112 = 0•20 +1•21+1•22+0•23+0•24+1•25+1•26
3-адическая запись числа 102 = 012013 = 0•30 +1•31+2•32+0•33+1•34
5-адическая запись числа 102 = 2045 = 2•50 +0•51+4•52
7-адическая запись числа 102 = 4027 = 4•70 +0•72+2•72
17-адическая запись числа 102 =0617 = 0•170 +6•171
Видим, что степень 0 у простых чисел в разложении числа 102 (5) дают не нулевые коэффициенты при нулевом члене в разложении по этому простому числу, а степень 1 – нулевые в нулевом члене разложения и ненулевой коэффициент при степени разложение 1.
Возьмем число 100 = 22• 30• 52• 70•…
2-адическая запись числа 100 = 00100112 = 0•20 +0•21+1•22+0•23+0•24+1•25+1•26
3-адическая запись числа 100 = 102013 = 1•30 +0•31+2•32+0•33+1•34
5-адическая запись числа 100 = 0045 = 0•50 +0•51+4•52
7-адическая запись числа 100 = 2027 = 2•70 +0•72+2•72
Если степень простого числа в разложении 2, то это означает, что р-адическое разложение по этому простому числу начинается с двух нулей, т.е. первым ненулевым членом в разложении является коэффициент при степени 2 основания счисления.
Иначе говоря, р-адический порядок γ = ordp(x) рационального числа x ∈ Q равен степени р, которая является делителем x.
2-адический порядок числа 102 = 1
2-адический порядок числа 100 = 2
3-адический порядок числа 102 = 1
5-адический порядок числа 102 = 0
5-адический порядок числа 100 = 2
7-адический порядок числа 102 = 0
17-адический порядок числа 102 =1
Тогда, поскольку р-адическая норма ||x||p = p-γ
Для р=2 ||102||2 = 2-1 , ||100||2 = 2-2 , для р=3 ||102||3 = 3-1 , для р=5 ||100||5 = 5-2 , ||102||5 = 5-0 =1
Так же, для примера, если р=2, то ord2(1/2) = -1 и ||1/2||2 = 2+1 , ord2(3) = 0 и ||3||2 = 1. Если р=3, то ord3(1/2) = 0 и ||1/2||3 = 1 , ord3(3) = 1 и ||3||3 = 3-1=1/3
Отрицательные р-адические числа
Рассмотрим 2-адические числа 12, 22, 32
……00012+ = 110= 1000…..2
……00102+ = 210= 01000…..2
……00112+ = 310= 11000….2
Отнимем 210 -310 = -110
С учетом правила разрядов получим:
| . | . | . | . | . | 0 | 0 | 0 | 1 | 0 | |
| - | . | . | . | . | . | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
-110 = ….111112+
Сложим -110+( -110)= -210
| . | . | . | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| + | . | . | . | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| . | . | . | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
-210= ….111102+
-310= ….111012+
-410= ….111002+
Посмотрим, что такое 2-адическое представление числа -1/310
-1/310=-110/310
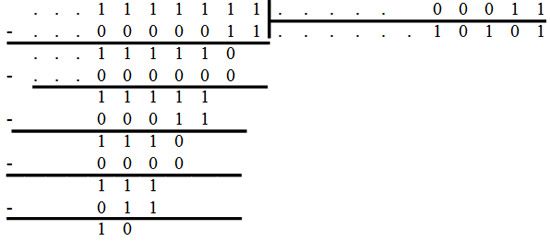
-1/310=…..010101012+ = …(01) 2+= (10)…. 2
Но что такое …1111 при основании 2?
Как я показал выше, -1 = 1•20+1•21+1•22+1•23+…. = 1/(1-2), где 1/(1-2) как бы формальная сумма бесконечного ряда со знаменателем прогрессии равным 2 и первым членом 1.
При р-адическом представлении всегда имеет место формула
-1 = (p-1)/(1-р) = (р-1)•р0+(р-1)•р1+(р-1)•р2+(р-1)•р3+….
т.е., например, для 3-адического представления
-110 = (3-1)/(1-3) = (3-1)•30+(3-1)•31+(3-1)•32…. = 0,2222…3 = ....22223+ или ….2222,03+
Проверим.
310 = 0•30+1•31+0•32+0•33+…. = ….00103+
410 = 1•30+1•31+0•32+0•33+…. = ….00113+
С учетом того, что это троичная система счисления, в которой коэффициенты при степенях 0,1, 2 и для которой в случае несимметричной системы таблица сложения имеет следующий вид
|
2 |
02 | 10 | 11 |
|
1 |
01 | 02 | 10 |
|
0 |
00 | 01 | 02 |
|
+ |
0 |
1 |
2 |
а это значит, что (2-1=1), (1-1=0), (0-1 =2 с уменьшением разряда), (0-2 =1 с уменьшением разряда), (2+1=0 с дополнением разряда, т.е. 2+1=3 =103) получаем
| . | . | . | . | . | 0 | 0 | 0 | 1 | 0 | |
| - | . | . | . | . | . | 0 | 0 | 0 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
-110 = (5-1)/(1-5) = (5-1)•50+(5-1)•51+(5-1)•52+…. =…..44445+ или …..4444,05+ = (4),05+
Вещественная 5-чная запись 110
110=0,4444….5= 0,(4) 5
Возьмем десятичное разложение 110:
вещественное 110 = 0,99999…10 = 0,(9).. 10
10-адическое -110 =..999999,0 10+= (9),010+=0, (9).. 10=(9).. 10
или 16-ричное разложение 110 :
вещественное 110 = 0,fffff… 16= 0,(f), (f =15)
16-адическое -110 =..fffff,016 = (f),0
или 7-ричное разложение 110:
вещественное 110 = 0,6666… 7=0,(6)
7-адическое -110 =..6666,07 = (6),0
Рассмотрим 2-ичное разложение рационального числа m/n, где m,n – взаимно простые, например (1/3)10:
вещественное (1/3) 10 = 0,010101…2 =0,(01)
2-адическое (-1/3) 10 =...01010101,02+= (01),0
Получается, что если одну периодическую последовательность цифр продолжить и влево и вправо от запятой, то хвост вправо от запятой даст некое рациональное число х с вещественной точки зрения, а хвост из таких же цифр, но влево от запятой даст (-х), но уже в p-адической записи.
Отметим еще, что умножение на p сводится к приписыванию нуля справа (или слева при канонической записи), так что целое p-адическое число делится на p тогда и только тогда, когда его «последняя» (т. е. крайняя правая) цифра есть нуль.
-110 = …..1111112+
(-410) = (-110) •22
-410 = 0•20+0•21+1•22+1•23+…. = 00111…2= …. 1111002+
Извлечение корней
Рассмотрим целые р-адические числа и сравнения, модуль которых есть степень простого числа. Например, рассмотрим сравнение х2 ≡ 2(mod7n)
Очевидно, что взятие остатка от деления 2 на 7 есть 2mod7 =0•7 +2 =2
Нам нужно найти некое 7-адичное число х такое, что взятие остатка от деления х2 на 7n есть 2.
При n=1 сравнение принимает вид:
х02≡ 2(mod7)
Это означает, что есть уравнение х02= 2+7•t0, где х0 , t0– целые. Деление правой части на 7 дает целое число t0 и остаток. Необходимо найти такое t0 , чтобы х0 было первым целым. При t0= 1 х02= 9, откуда х0 =± 3. Далее будем рассматривать значение х0 = 3 (хотя решение х0 = - 3 так же имеет смысл и дает свое значение 7-адического √2).
Следующая цифра ищется из сравнения
х12≡ 2(mod72), где х1 = х0 + 7•t1, где х1 , t1– целые, тогда
(х0 + 7•t1)2 = х02+2• х0• 7•t1+72•t12≡ 2(mod72),
Поскольку t12 целое, то 72•t12≡ 0(mod72), отсюда
х02+2• х0• 7•t1 ≡ 2(mod72).
Подставим значение х0 = 3, получим:
9+6• 7•t1 ≡ 2(mod72).
Принимая во внимание, что слагаемое, стоящее в какой-либо части сравнения, можно переносить в другую часть, изменив его знак на обратный, получаем, перенося 2 справа налево.:
7+6• 7•t1 ≡ 0(mod72), или 7• (1+6• t1 ) ≡ 0(mod72),
Последнее выражение эквивалентно
1+6• t1 ≡ 0(mod7)
Таким образом, нужно найти такое t1, что при делении 1+6• t1 не будет остатка. Откуда t1= 1
Сделаем еще две итерации.
Первая
х1 = х0 + 7•t1+ 72•t2= 3+7+72•t2=10+72•t2
Имеем сравнение
(10+72•t2)2 = 100+20• 72•t2+74•t22≡ 2(mod73),
Поскольку t22 целое, то 74•t22≡ 0(mod73). Отсюда, перенося 2 в левую часть, имеем
98+20• 72•t2 = 2• 72+20• 72•t2 = 72•(2 +20•t2)≡ 0(mod73),
Это эквивалентно
2 +20•t2 ≡ 0(mod7).
При делении левой части на 7 не определенный остаток будет
(2+6•t2), поскольку 14•t2 делится на 7 без остатка, т.е. мы должны решить уравнение
2 +6•t2 ≡ 0(mod7). Откуда t2= 2
Вторая
х2 = х0 + 7•t1+ 72•t2+ 73•t3= 3+7+72•2+ 73•t3=108+73•t3
Проводя такие же преобразования, имеем:
73•2• (17 +108•t3)≡ 0(mod74),
Учитывая, что обе части сравнения можно разделить на их общий делитель, взаимно простой с модулем, в данном случае 2, получаем сравнение
17 +108•t3≡ 0(mod7),
Для упрощения вычислений убираем из левой части числа кратные модулю (14+105•t3). Тогда 3 +3•t3≡ 0(mod7), откуда t3= 6, поскольку 21 самое близкое целое число, которое делится на 7 без остатка
Видно, что этот процесс мы можем продолжать до бесконечности. Мы получим последовательность
х0 , х1 ,….. хn ,…..
обладающую свойствами
х0≡ 3(mod7)
хn≡ хn-1 (mod7n)
хn2≡ 2(mod7n+1)
В результате получаем, что √27 = ...266421216213 = 3+7•1+72•2+ 73•6+ ……
Но не всякие корни можно записать в р-адических системах счисления.
Например, в 7-адичной системе счисления нельзя записать √3, поскольку никакое целое число при возведении в квадрат по модулю 7 не даёт 3 (т. е. нельзя подобрать последнюю цифру).
Древовидная структура р-адических чисел
Поле р-адических чисел имеет простую геометрическую структуру. Оно представимо в виде однородного дерева с ветвлением на р частей в каждой вершине. Это следует из смысла сравнения по модулю. Такое дерево иногда называют иерархическим или лексикографическим. Конкретное число получается, если следовать по определенному пути по его ветвям, последовательно выписывая цифры в вершинах. Каждому числу соответствует свой путь и наоборот.
Покажу на двух примерах как строятся деревья для р=2 и 3.
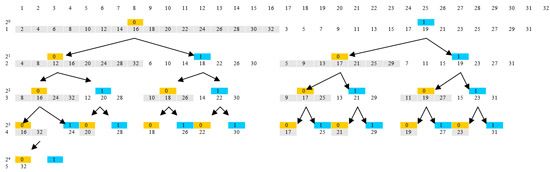
2-адичное представление чисел (бинарное дерево)
|
| |
Числа из строки 1 {2,4,…32} сравнимы по модулю 2
2≡ 4 ≡ 6….≡32 (mod2) = 0 = 0•20, в двоичном коде имеют одинаковое окончание …0
Числа из строки 1 {3,5,…31} сравнимы по модулю 2
3≡ 5≡ 7….≡31 (mod2) = 1 (остаток) = 1•20, в двоичном коде имеют одинаковое окончание …1
Числа из строки 2 {4,8…32} сравнимы по модулю 4
4 ≡ 8….≡32 (mod4) = 0 =0•20+0•21, в двоичном коде имеют одинаковое окончание …00
Числа из строки 2 {6,10,…30} сравнимы по модулю 4
6≡ 10≡ 14….≡30 (mod4) = 2 (остаток) =0•20+ 1•21, в двоичном коде имеют одинаковое окончание …10
Если мы от каждого числа из {6,10,…30} отнимем остаток 2, то получим {4,8…32}
Числа из строки 2 {5,9…29} сравнимы по модулю 4
5 ≡ 9….≡29 (mod4) = 1 = 1•20+0•21, в двоичном коде имеют одинаковое окончание …01
Числа из строки 2 {7,11,…31} сравнимы по модулю 4
7≡ 11….≡31 (mod4) = 3 (остаток) =1•20+ 1•21, в двоичном коде имеют одинаковое окончание …11
Числа из строки 3 {8,16,24…32} сравнимы по модулю 8
8 ≡ 16….≡32 (mod8) = 0 =0•20+0•21+0•22, в двоичном коде имеют одинаковое окончание …000
Числа из строки 3 {12,20,28} сравнимы по модулю 8
12≡ 20≡ 28 (mod8) = 4 (остаток) =0•20+0•21+1•22 , в двоичном коде имеют одинаковое окончание …100
Если мы от каждого числа из {12,20,28} отнимем остаток 4, то получим {8,16…32}
Числа из строки 3 {10,18…26} сравнимы по модулю 8
10 ≡18….≡26 (mod8) = 2(остаток) =0•20+1•21+0•22, в двоичном коде имеют одинаковое окончание …010
Если мы от каждого числа из{10,19…26} отнимем остаток 2, то получим {8,16…32}
Числа из строки 3 {14,22,30} сравнимы по модулю 8
14≡ 22≡30 (mod8) = 6 (остаток) =0•20+1•21+1•22, в двоичном коде имеют одинаковое окончание …110
Если мы от каждого числа из{14,22,30} отнимем остаток 6, то получим {8,16…32}
Числа из строки 3 {9,17,25} сравнимы по модулю 8
9≡ 17≡25 (mod8) = 1 (остаток) =1•20+0•21+0•22, в двоичном коде имеют одинаковое окончание …001
Если мы от каждого числа из {9,17,25} отнимем остаток 1, то получим {8,16, 24}
Числа из строки 3 {13,21,29} сравнимы по модулю 8
13≡ 21≡29 (mod8) = 5 (остаток) =1•20+0•21+1•22, в двоичном коде имеют одинаковое окончание …101
Если мы от каждого числа из{13,21,29} отнимем остаток 5, то получим {8,16…32}
И т.д.
Число из строки 4{24} по модулю 32
24 mod32 = 24(остаток) = 0•20 +0•21+0•22+1•23+1•24, в двоичном коде 11000
И т.д.
Выделенные в таблице 0 (желтым) и 1(синим) есть коэффициенты при основании в степени
Остатки от деления на 2n составляют множество {0,1…2n -1}
n=1→ {0,1}; n=2→ {0,1,2,3}; n=3→ {0,1,..7};
Первичное числовое множество N={1,2,3..}; разбивается на 2 по mod2 (2 множества)
Каждое из образовавшихся множеств разбивается на 2 по mod4 (4 множества)
Далее каждое из вновь образовавшихся разбивается так же на 2 по mod8 (8 множеств) и т.д.
Получаем иерархическое дерево, например, разложение целых положительных чисел на бинарном дереве Кейли
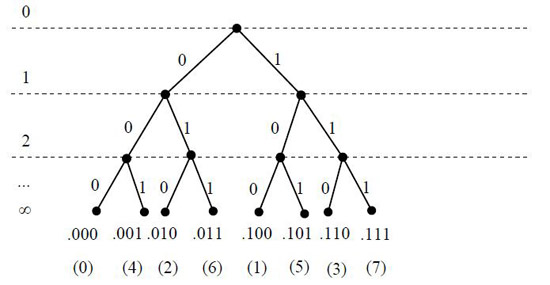
Теперь рассмотрим 3-адичное представление чисел (тренарное дерево)
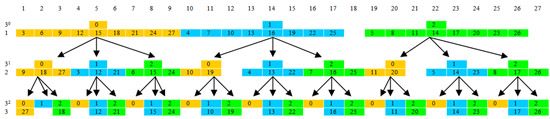
|
| |
Числа из строки 1 {3,6,…27} сравнимы по модулю 3
3≡ 6 ….≡27 (mod3) = 0 = 0•30, в троичном коде имеют одинаковое окончание …0
Числа из строки 1 {4,7,…25} сравнимы по модулю 3
4≡ 7….≡25 (mod3) = 1 (остаток) = 1•30, в троичном коде имеют одинаковое окончание …1
Числа из строки 1 {5,…26} сравнимы по модулю 3
5≡ 8….≡26 (mod3) = 2 (остаток) = 2•30, в троичном коде имеют одинаковое окончание …2
Числа из строки 2 {9,18,27} сравнимы по модулю 9
9≡ 19 ≡27 (mod9) = 0 = 0•30 +0•31, в троичном коде имеют одинаковое окончание …00
Числа из строки 2 {3,12,21} сравнимы по модулю 9
3≡ 12≡21 (mod9) = 3 (остаток) = 0•30 +1•31, в троичном коде имеют одинаковое окончание …10
Числа из строки 2 {6,15,24} сравнимы по модулю 9
6≡ 15≡24 (mod9) = 6 (остаток) = 0•30 +2•31, в троичном коде имеют одинаковое окончание …20
Числа из строки 2 {10,19} сравнимы по модулю 9
10≡ 19 (mod9) = 1 = 1•30 +0•31, в троичном коде имеют одинаковое окончание …01
Числа из строки 2 {4,13,22} сравнимы по модулю 9
4≡ 13≡22 (mod9) = 4 (остаток) = 1•30 +1•31, в троичном коде имеют одинаковое окончание …11
Числа из строки 2 {6,15,24} сравнимы по модулю 9
7≡ 16≡25 (mod9) = 7 (остаток) = 1•30 +2•31, в троичном коде имеют одинаковое окончание …21
Число из строки 3 {27} по модулю 27
27 mod27 = 0 = 0•30 +0•31+0•32, в троичном коде имеют одинаковое окончание ..000
Число из строки 3{18} по модулю 27
18 mod27= 18(остаток) = 0•30 +0•31+2•32, в троичном коде 200
Число из строки 3 {12} по модулю 27
12 mod27 = 12 (остаток) = 0•30 +1•31+1•32, в троичном коде 110
Число из строки 3 {21} по модулю 27
21 mod27 = 21(остаток) = 0•30 +1•31+2•32, в троичном коде 210
Количество кодируемых чисел (p-1)pk-1, где р - основание, а k – количество разрядов
Так при основании 3 и k=4 (т.е. начиная с 1000) кодируются (3-1) • 34-1 =2•27= 54 числа от 27 до 80, а при основании 4 и k=2 (т.е. начиная с 10) кодируются (4-1) • 42-1 =3•4= 12 числа от 4 до 15
Адельные числа
Напомню, что существует бесконечно много различных р-адических представлений. Поля р-адических чисел для различных простых р неизоморфны. Действительно, как можно сохранить структуру при отображении, например, бинарного дерева на тренарное. Поэтому 2-адическое описание не эквивалентно 3-адическому. Отсюда вытекает проблема построения р-адических моделей для микромира: какое простое р следует выбирать для систем координат в планковском мире?
Одним из решений этой проблемы является рассмотрение не р-адической системы координат для фиксированного р, а адельной системы координат, которая содержит и вещественную, и все р-адические координаты.
Адельные числа были введены в математику немного раньше ультраметрики, на рубеже 1930-1940-х годов. Родоначальником аделей был французский математик Клод Шевалле. Суть адели сводится к тому, что это вектор или бесконечная последовательность чисел, где на первом месте стоит произвольное действительное (вещественное) число, а на всех остальных – p-адические выражения для того же самого числа по всевозможным нарастающим значениям простого p. Благодаря такой конструкции они одновременно демонстрируют свойства архимедовой и фрактальной (неархимедовой) топологии.
Таким образом вектор (а∞, a2, a3, …) где а∞ ∈ R (вещественная компонента), ap ∈ Qp (р-адическая компонента для всех р) с дополнительным условием ||a||p ≤ 1 для всех достаточно больших р называется аделью.
УЛЬТРАМЕТРИКА
Как было показано выше на поле Qр можно задать метрику dp(x,y)= |x-y|p, x,y ∈ Qр индуцированную нормой ||•||p. При этом Qр становится полным метрическим пространством. Так как норма ||•||p неархимедова, то соответствующая ей метрика dp удовлетворяет сильному неравенству треугольника
dp(x,y) ≤ max[dp(x,z)p, dp(z,y)], x,y,z ∈ Qр
т.е. длина любой стороны треугольника не больше, чем наибольшая из длин двух других сторон.
Метрика такого типа называется ультраметрикой, а – Qр ультраметрическим пространством для любого р.
Какие же свойства у этого ультраметрического пространства?
1. Нарушение аксиомы Архимеда, т.е., например, при сложении отрезка с самим собой он может стать короче, чем был
2. Все треугольники равнобедренные. Нет там золотого сечения.
3. Любая точка внутри окружности, шара может быть ее центром. Шар может иметь бесконечно много радиусов.
4. Шар и сфера одновременно открыты и замкнуты в Qр. Множества, являющиеся одновременно открытыми и замкнутыми, называются открыто-замкнутыми.
5. Два шара в Qр имеют непустое пересечение тогда и только тогда, когда один из них содержится в другом, т.е. два шара в Qр либо не пересекаются, либо один из них содержится в другом.
6. Множество всех шаров в Qр счетно.
7. Пространство Qр вполне несвязно. Это означает, что в нем нет никаких связных подмножеств, кроме пустого множества и одноточечных множеств.
8. Пространство имеет нулевую размерность.
9. Невозможно изометрически вложить ультраметрическое пространство, содержащее n+1 точку, в Rk , k<n (теорема А. Лемина), только в Rn. Следовательно, например в R3 может быть вложено только ультраметрическое пространство, содержащее 4 точки.
10. Физическое (метрическое) пространство может быть представлено в виде древовидной решетки. Обратное, если расстояние между точками удовлетворяет усиленному неравенству треугольника, то подпространство, натянутое на них, является эвклидовым.
Аналогий с привычным нам поведением объектов и с физическими процессами в ультраметрическом пространстве нет. Возможно, что только капли ртути создают некоторую аналогию: они либо раздельны, либо соединяются в одну каплю. Может поэтому, как повествуют древние манускрипты, ртуть использовали в виманах?
Отметим, что для a,b ∈ Zp (множество р-адических целых чисел) всегда dp(a,b)= p-i для подходящего i = 0,1,2,….,∞. Более того, dp(a,b)= p-i тогда и только тогда, когда
a=……ai+1aici-1…c0 p+
b=……bi+1bici-1…c0 p+
и a≠b. Случай i = ∞ означает, что dp(a,b)= 0, т.е. что a = b.
В этом случае a≡b (mod pi) или, что тоже самое, a mod pi = b mod pi
Покажу на примерах вычисление расстояния, нарушение аксиомы Архимеда и выполнение п.1. свойств ультраметрических пространств.
Например, абсолютная величина (норма) 2-адического целого числа есть расстояние от него до 0: ||a||2 = d2(a, 0). Т.о., d2(a, b) = ||a − b||2. Например,
. . . 1010101012+ = −1/3
. . . 0000001012+ = 5, т.е. количество одинаковых цифр 4
Тогда d2(−1/3, 5) =1/24=1/16
Иными словами, −1/3 ≡ 5 (mod 16); но −1/3 ≠ 5(mod 32).
Теперь возьмем точки 0, 2, 4; тогда d2(0, 2) =||2||2 = 1/2 , d2(2, 4) = ||4 − 2||2 = 1/2 , но d2(0, 4) = ||4||2 = 1/4 . Удвоенный отрезок оказался вдвое короче исходного.
Это и означает, что в p-адическом мире Zp не выполняется аксиома Архимеда: прикладывая отрезок сам к себе, мы получили отрезок короче, чем исходный.
МИР МЫШЛЕНИЯ
Начиная с 1988 года, в своих работах я все время писал, что субстанцией мышления является слабая метрика, к которой применим нестандартный анализ. В качестве элементов слабой метрики я предлагал использовать гипердействительные бесконечно малые ε, которые ассоциировались со словами, мыслями и вообще с целостностями нашего чувственного мира, такими как атом, клетка, организм, Биосфера, звездная система, галактика и т.д. Позже, рассматривая возникновение пространства как протяженности и времени как длительности из слабой метрики, т.е. из пространства мышления, я предложил идею взаимодействия ε слабой метрики и обратного к ней явления – галактики, которая описывалась бы гипердействительным бесконечно большим D. Такая идея сама по себе решала проблему антропного принципа: «Мы видим Вселенную такой, потому что только в такой Вселенной мог возникнуть наблюдатель, человек». Она разрешалась тем, что и в основе мышления человека наблюдателя и в основе Вселенной лежит одна и та же субстанция, причем материальная. Но свойства этой материи принципиально отличны от свойств материи, которую мы ассоциируем с веществом. Именно тогда была предпринята попытка понять сложную структуру точки пространства протяженности, которая возникала из сложной структуры взаимодействий в слабой метрики. Речь шла не об абстрактном математическом объекте, а о реальном физическом, который сейчас можно сопоставить со сферой диаметром длины Планка. Если снаружи мы имеем упорядоченное пространство, но внутри нет. Причем это касалось не только пространственного описания, но и временного. Тогда я дал такое определение физической точки: сложный нульмерный многоуровневый параметрический объект (система) с фрактальной топологией, в которой происходит движение перехода между уровнями с изменением энергетического состояния; нульмерная структура с параметрической фрактальной топологией. Развитие р-адических чисел и р-адического анализа показало, что такое определение, возможно, близко к реальному явлению.
Нульмерное - потому что любое ультраметрическое пространство имеет нулевую размерность.
Фрактальное – потому что древовидная структура р-адических чисел фрактальна.
Параметрическая – потому что от простого числа р зависит структура пространства физической точки, которая не изоморфна структуре пространства с другим р.
Единственное, что в этом определении претерпело изменение, так это понимание того, что в этом мире нет привычного нам времени, а в зависимости от абстракции в рассмотрении уровня организации материи есть логическое время, квантовое и привычное нам время как длительность, которое нельзя оторвать от представления о пространстве как протяженности. При этом логическое время – это время слабой метрики, а квантовое – физической точки. В реальности все они связаны.
Поскольку мышления происходит на субстанции, из которой произошли и с которой связаны все процессы во Вселенной, как пространства существования динамической материи, то сами процессы мышления влияют на физические процессы во Вселенной. Если наше мышление происходит в слабой метрике на уровне, связанной с атомами, то мы не заметим этого влияния. Но, если кто-то мыслит на уровне Биосферы, то небольшое изменением в параметрах Биосферы, как целого, может привести к существенным изменениям в фазовых траекториях движения ее частей, а значить людей, цивилизаций. Те, кто мыслят на уровне организма, могут влиять на параметры организма, а значить влиять на поведение отдельных клеток этого организма, что в некоторых случаях может приводить к самоизлечению.
В этом разделе я кратко представлю подходы А.Ю. Хренникова [11] к описанию ментальных пространств на основе р-адического анализа. Однако считаю, что он не верно отождествляет духовные пространства с ментальными. Если у элементов ментальных пространств есть границы, то дух границ не имеет. Более того, субстанция духа, или той его части, что мы можем ассоциировать с субстанцией Отображения, является основанием слабой метрики – ментального пространства. Между этими двумя понятиями я поставил знак соответствия, однако структурно это разные уровни организации материи. Вследствие одномоментного, с нашей точки зрения, раскрытия слабой метрики в пространство-время, ментальное пространство есть пространство физической точки, образованной из слабой метрики, а потому неотъемлемой от нее и несущей основные ее черты.
Итак, что есть ментальное пространство А.Ю. Хренникова?
Во-первых, оно не непрерывно, т.е. мысли нельзя делить до бесконечности, или это означает, что пространство не является связанным. «Любое p-адическое дерево можно разбить на две части, не имеющие общей границы или, что эквивалентно, на две непересекающиеся части, являющиеся одновременно и открытыми, и замкнутыми» .[11, с. 11]
Во-вторых, оно дискретно и обладает иерархической структурой, т.е. для двух ментальных объектов всегда существует некоторый ментальный объект, который стоит в иерархической системе выше указанных двух.
В-третьих, оно не является однородным, т.е. существует жесткая иерархия: корень, ствол, ветви, ответвления, листья.
В-четвертых, это пространство ультраметрическое, т.е. два психических состояния являются близкими, если у них достаточно длинная общая часть дерева.
В-пятых, оно не является упорядоченным, т.е. нельзя сравнить два произвольных ментальных объекта.
Для описания таких пространств А.Ю. Хренников предложил использовать m-адические деревья (m – натуральное число). Точками этого пространства являются ветви деревьев, т.е. m-адические числа (здесь m – целое число), которые представляют психические состояния. Используя психические координаты в виде m-адических чисел он ввел аналоги твердых физических тел – ассоциации и идеи. Они представлены соответственно в виде шаров и множеств шаров в ультраметрическом ментальном пространстве. Здесь возникает аналогия с ε образованиями в слабой метрики, которые можно представить как шары. Главное здесь, что шары либо существуют отдельно друг от друга, либо один включает другой, создавая иерархию.
Геометрически ассоциации можно представить как пучок ветвей m-адического дерева, а идеи, как множество таких пучков.
Р-адическую модель сознания была так же рассмотрена М. Питканеным [12]. Его подход был основан на кодировании психической иерархии с помощью р-адических чисел.
А.Ю. Хренников считает, что идея представления психических процессов с помощью чисел восходит к идеям Платона, затем Аристотеля и Лейбница.
Приведу выдержки из его работы [11].
«Учитывая огромную роль, которую идеи Аристотеля сыграли в дальнейшем развитии науки, рассмотрим более детально его взгляды па соотношения между числами, духовными объектами и физическими объектами. Фундаментальным литературным источником являются «Категории». В течение тысячелетий «Категории» анализировались тысячи раз с точки зрения философии и логики. Мы же (по-видимому, впервые за тысячи лет) собираемся провести математико-когнитивный анализ «Категорий». С этой точки зрения фундаментальную роль играет гл. 6 «Количество»: «Что касается количества, то одно раздельно, другое непрерывно, и одно состоит из частей, имеющих определенное положение по отношению друг к другу, а другое — из частей, не имеющих такого положения. Раздельны, например, число и слово, непрерывны — линия, поверхность, тело, а кроме того, время и место. В самом деле, у частей числа нет никакой общей границы, где соприкасались бы его части; так, например, если пять есть часть десяти, то пять и пять не соприкасаются ни на какой общей границе, а стоят раздельно; также три и семь не соприкасаются ни на какой общей границе. И вообще у числа нельзя указать общую границу его частей; они всегда стоят раздельно, поэтому число принадлежит к раздельным количествам. И таким же образом и слово принадлежит к раздельным количествам. Линия же непрерывна, ибо можно указать общую границу, где соприкасаются ее части, — точку, а у поверхности — линию: ведь части плоскости соприкасаются на некоторой общей границе. Таким же образом и у тела можно указать общую границу — линию или поверхность, где соприкасаются части тела. Также и место и время принадлежат к таким количествам: настоящее время соприкасается с прошедшим временем и с будущим. В свою очередь и место принадлежит к непрерывным количествам: ведь части тела, которые соприкасаются на некоторой общей границе, занимают определенное место; стало быть, и части места, которые занимает каждая из частей тела, соприкасаются на той же границе, где соприкасаются и части тела. Поэтому и место, можно сказать, непрерывное количество: ведь его части соприкасаются по одной общей границе».
Отметим, что под числами Аристотель понимал натуральные числа (1,2,3…). Как уже отмечалось, понятие вещественного числа (соответствующего точке прямой линии) было выработано только в конце XIX века. Во времена Аристотеля оцифровка точек прямой или плоскости казалась невозможной. Прошли еще сотни и сотни лет, пока Декарт взглянул в зарешеченное окно и оцифровал пространство.
Аристотель, по существу, говорит об оцифровке духовных объектов, например слов. Он подчеркивает, что с количественной точки зрения натуральные числа и духовные объекты весьма близки, и они фундаментально отличны от непрерывных физических структур. Вообще, удивительно, что в главе «Количество» слова (как представители духовных объектов) появляются уже во втором предложении и постоянно обсуждаются с количественной точки зрения.
Итак, по Аристотелю числа (натуральные) и слова составляют один класс объектов, а линии, поверхности, тела — в общем, элементы физического пространства — другой, совершенно отличный класс объектов. Основным характеристическим свойством физических объектов является непрерывность. С современной топологической точки зрения весьма интересно, как Аристотель определяет непрерывность. По Аристотелю объект непрерывен, если всегда можно указать общую границу, где соприкасаются его части. Как уже отмечалось, в современной топологии пространства такого типа называются связными. Связное пространство нельзя представить в виде объединения двух («достаточно хороших») частей, не имеющих общей границы. Пространство же, которое можно разбить на части, не имеющие общей границы, называются несвязными. По существу, Аристотель писал, что числа (натуральные) и слова составляют несвязные топологические пространства. В несвязном пространстве мы не можем соединить любые две точки непрерывной траекторией. По Аристотелю в мире духовных объектов мы не можем перейти от одного объекта к другому по непрерывной траектории. Значит, каждый шаг в развитии духа представляет собой скачок, сингулярность.
Более того, пользуясь современной математической терминологией, мы можем сказать, что Аристотель имел в виду, что пространства чисел и духа являются вполне несвязными топологическими пространствами, т.е. любое их подпространство тоже несвязно.» [с.15-17]
«Далее Аристотель обсуждает другое важнейшее отличие физических количеств, а также числовых и духовных количеств, а именно — наличие порядковой структуры в физическом пространстве и отсутствие ее в числовых и духовных пространствах: «Далее, одни количества состоят из частей, имеющих определенное положение по отношению друг к другу, а другие — из частей, не имеющих такого положения; так, части линии имеют определенное положение по отношению друг к другу: ведь каждая из них расположена где-то, и можно было бы различить и указать, где каждая находится на плоскости и с какой частью из остальных она соприкасается. Точно так же имеют определенное положение и части плоскости: можно точно так же указать, где находится каждая из этих частей и какие части соприкасаются друг с другом. И равным образом — части тела и части места. У числа же нельзя было бы показать, каким образом его части имеют определенное положение по отношению друг к другу, или где они находятся, а также какие части соприкасаются друг с другом. Нельзя это показать и у частей времени: ведь ни одна часть времени не неподвижна; а как может то, что не неподвижно, иметь определенное положение? Скорее можно было бы сказать, что время имеет некоторый порядок в том смысле, что одна часть времени существует раньше, а другая — позже. Точно так же обстоит дело и с числом — в том смысле, что один указывают в счете раньше, чем два, а два — раньше, чем три; и именно в этом смысле у числа имеется, пожалуй, некоторый порядок, а положение (для него) вовсе нельзя указать. И точно так же произнесенное слово: ни одна часть его не неподвижна, а каждая уже сказана, и ее уже нельзя ухватить; поэтому у частей слова нет положения, раз ни одна из них не неподвижна. Итак, одни количества состоят из частей, имеющих определенное положение, другие — из частей, не имеющих положения».
Заметим, что следует отличать положение частей (некоторого более общего объекта) по отношению друг к другу и положение части по отношению к объекту. Аристотель обсуждает положение частей. По существу, он пишет, что отношения порядка, основанного на взаимном расположении равноправных частей в мире духа (и натуральных чисел), нет. Остается только удивляться, до чего же хорошо р-адическая модель «ложится» на философию Аристотеля: точно также невозможно ввести порядковую структуру на множестве р-адических чисел. Это множество неупорядочено. В отличие от числовой прямой на р-адическом дереве существуют несравнимые части.
В то же время на р-адическом дереве существует жесткая иерархия, основанная на положении части по отношению к более общему объекту. Я рассматриваю древовидную структуру этой иерархии в качестве важнейшей отличительной черты духовных пространств.» [с.18-19]
«…человеческое сознание моделируется с помощью поля так называемой ведущей волны (термин из квантовых моделей Луи Де Бройля и Дэвида Бома) на духовном пространстве. Рассматриваемое поле (ведущая волна) сознания является чисто информационным полем. В частности, оно не переносит «настоящей физической энергии». Одной из важнейших отличительных черт стандартной теории ведущей волны, используемой в обычной «физической» квантовой механике, является нелокальность. Квантовые частицы, находящиеся на огромных расстояниях друг от друга, могут взаимодействовать с помощью так называемого квантового потенциала при полном отсутствии классических взаимодействий. Наша р-адическая модель наследует нелокальность, присущую стандартной R-модели ведущей волны (бомовской механике). Однако р-адическая нелокальность является нелокальностью не в физическом пространстве Rm, а в духовном пространстве Qpm . В модели духовной ведущей волны (поля сознания) духовные объекты (мысли, идеи, образы, чувства) могут взаимодействовать при полном отсутствии классических физических и духовных взаимодействий. Возникает коллективная ведущая волна (или коллективное поле сознания).» [с.20]
«В наших моделях р-адическая метрика имеет ясную когнитивную интерпретацию. Если две идеи имеют обширную общую ассоциацию, то они близки в р-адической метрике. Итак, р-адическая метрика — это расстояние на духовном пространстве, основанное на общности ассоциаций. Таким образом, наши р-адические модели описывают ассоциативное мышление» [с.21]
Еще раз считаю необходимым отметить, что применять к описываемым пространствам термин «духовные» некорректно. Дух – другое явление, но которое непосредственно связано с ментальным пространством. Дух не только образует первичные понятия, задает им границу, но и определяет порядок древовидной структуры, т.е р - сложность структуры. Дух дышит в этой структуре, но не сводится к ней.
В 1984 году А.Н. Паршин указал на связь р-адических чисел с формальной логикой и свойствами систем, выражаемых формальными языками и высказал идею о необходимости объединения вещественных и р-адических чисел для описания оппозиции «вещи – отношения» [13, примечание 17] и отметил 2-адические числа как модель мира идей Платона [14].
Описывая выше образы целых р-адических чисел и простых целых чисел, мы отметили, что цифры в них одни и те же, но порядок их представления меняется.
Представим, например, транспонирование матрицы 4-ого ранга
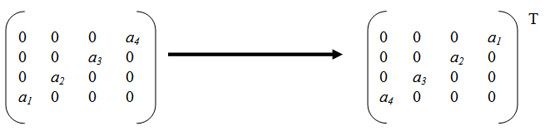
Видно как поменялись местами числа по диагонали. Таки образом, одну можно ассоциировать с р-адическим числом, а другую с обыкновенным.
Но А•АТ ≠ 1
Если представить себе, что слабая метрика ассоциируется с целыми числами, а обратная ей галактика – с обратными значениями целых чисел, то, как я полагаю, ε⊗D = цепной дроби 1/(1+1/(1+… , которая прерывается для возобновления цикла, что при определенном нормировании дает 0, 618…, но конечное число, которое можно представить в виде рационального числа. Именно поэтому рациональные числа – физические, поскольку являются результатом взаимодействия двух пространств: архимедова и неархимедова. Именно поэтому с помощью аделей, как составных числах, очень удобно описывать явления.
МИР ВЕЩЕСТВА
Важным качеством квантового мира является нелокальность. Есть множество ее интерпретаций. Но главное для всех интерпретаций, что взаимодействие несиловое, коррелятивное. Для меня в основе этой корреляции лежит субстанция Отображения, которая еще не является материей, поскольку не оформлена, т.е. не имеет границ. Именно она является представителем Духа.
Чем энергетичнее движение, тем влияние нелокальности уменьшается. В абстрактном пределе мы имеем газокинетическую модель без учета взаимодействий, т.е. когда каждое последующее состояние определяется только предыдущим.
Абстракции р-адических чисел и вещественных есть взгляд на мир со стороны рациональных чисел, со стороны завершенных циклических процессов.
Одно расширение рациональных чисел ведет к слабой метрике, другое к евклидовому пространству. Последнее – неразрывно с веществом, которое имеет образ, символ в слабой метрике. Вещество и символы неотделимы друг от друга так же, как части проблемы Единое-Многое. Можно сказать, что вещество – носитель энергии, символ – носитель свойств, или качеств.
Эвклидово пространство не более чем математическая модель для реального физического пространства, которую можно применять при описании процессов на больших расстояниях. Как считает математик «Вещественная» и «арифметическая» картины мира находятся в отношении дополнительности
Эту мысль он сформулировал в 1987 г., выступая с докладом на международной Летней школе по конформной инвариатности и струнной теории, которая в румынском курортном городке Пояна Брашов в Карпатах.
ПРОНИКНОВЕНИЕ МИРОВ
Р-адические числа и фрактальность
Впервые на связь р-адических чисел с фрактальными множествами и физическими проблемами указал ученик Банаха Станислав Мартин Улам в середине XX века.[16] По его представлениям р-адические числа являются инвариантами процессов бесконечного деления вещества и общей топологией различных областей Вселенной, включая объекты с противоположными свойствами, такими как, например, протон и электрон. Он констатировал, что р-адическая топология совпадает с топологией канторова совершенного множества C и может рассматриваться как альтернатива континуальным теориям физики и возможности выражения физически осмысленных величин.
Его выводы кратко сформулированы в работе [17]
«Распространение анализа на описание комбинации дискретности с непрерывностью для физических свойств приводит к структуре канторова совершенного множества. Соответственно не только действительные числа характеризуют физически содержательные величины.
Множество материальных точек является ни евклидовым континуумом, ни набором дискретных точек. Модели канторова множества могут быть адекватны для физических моделей, которые топологически являются ни евклидовым континуумом (теория поля), ни соответствуют понятию элементарных частиц, внутренность которых далее не анализируется (как в современной теории кварков), то есть в случае, когда происходят непрекращающиеся процессы подразделения физических сущностей, таких как масса.
Подобные процессы приводят к распределениям типа канторова совершенного множества с топологией более соответствующей р-адическим, нежели вещественным числам.
Канторово множество важно и как модель конфигурационного пространства, так и фазового и, в конце концов, эта конструкция должна быть осуществлена в пространстве Минковского-Лоренца.
В этом случае физические структуры представляются с бесконечно увеличивающейся сложностью, и аксиома регулярности теории не может быть удержана. Также теряет своё значение в физике и аксиома непрерывности….
По словам Улама: «похоже на то, что физические явления радикально меняют свои физические свойства в малом». Поэтому дальнейшая геометризация физики не может быть осуществлена простым обобщением понятий евклидовой геометрии, так как дифференциальная метрика никогда не отразит существенных свойств непрекращающихся процессов деления, но должна основываться на радикальных изменениях локальной топологии (так как в канторовом множестве).
… физика не была бы возможной, если электрон и протон не были бы во многом тождественны. Если это подобие или идентичность подмножеств Вселенной не существует, не могло бы быть никакой физики». [17, с.1781-1785].
Получается, что так же как и фракталы, р-адические числа являются инвариантами процессов бесконечного деления материи: вещественные числа связны, отражают протяжённость, р-адические и канторово множество полностью разрывны, моделируют делимость.
Рассмотрим образование канторова множества, канторовой пыли.
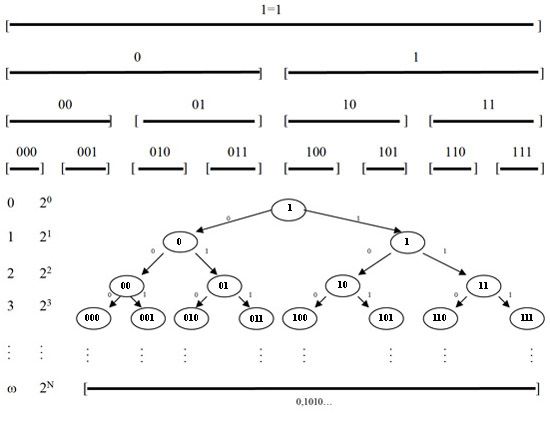
Рис. Образование канторовской пыли совместно с бинарным лексографическим деревом.
Определим
С0 =I= [0,1] С1 = [0,1/3] U [2/3,1 ], С2 = [0,1/9] U [2/9,1/3 ] U [2/3,7/9 ] U [8/9,1 ],…
Каждое множество Сn является объединением 2n замкнутых отрезков длины 3-n, и С0
⊃ С1 ⊃ С2....
Канторов множество определяется как
С = ⋂Сn , n =[0, ∞)
Канторов множество имеет меру нуль в том смысле, что сумма длин удаленных отрезков равна 1.
Если представить действительные числа, принадлежащие единичному отрезку [0,1] в виде бесконечных дробей по основанию 3, то получим, что канторов множество С состоит из всех точек отрезка I, которые нельзя представить в виде дробей по основанию 3 с помощью цифр 0 и 2.
Теперь рассмотрим множество канторовского типа в качестве геометрической модели множества р-адических чисел.
Так множество 2-адических чисел Z2 с 2-адической нормой ||•||2 гомеоморфно канторовому множеству С с евклидовой абсолютной величиной ||•||. Этот гомеоморфизм осуществляется с помощью отображения:
Σ ak•2k → Σ2•ak/3k+1 , k = [0, ∞)
Если взять 2-адические числа без дробной части, то при отображении они отобразятся на некоторую разновидность канторовского множества: от отрезка длины 3 отбрасываем правую треть, от каждой из оставшихся третей отбрасываем правую треть, и так бесконечное количество раз.
Поскольку такое канторовское множество упорядочено, мы можем этот порядок перенести на 2-адические числа. Но при этом мы получим, что между числами (далее нижний индекс - основание системы счисления) (1)0,02 и 12, которые отображаются на вещественные числа 0,(1)3=1/3(1-1/3)=1/2 и 13 нет ни одного числа, которое было бы больше одного и меньше другого. Т.е. разъединив те точки, которые слипались при отображении, мы создали в нашем отрезке «дырки».
Для Zр существует такое отображение
Σ ak•рk → Σ2•ak/(2р-1)k+1 , k = [0, ∞)
В целом поле Qp гомеоморфно канторовскому множеству на вещественной оси.
Еще раз подчеркну, что:
- Канторово множество континуально,
- Канторово множество имеет топологическую размерность 0,
- Каждый нульмерный метризуемый компакт без изолированных точек гомеоморфен канторову множеству.
Итак, поскольку ментальное и евклидовое пространства существуют как единое целое, то процессы, происходящие в одном, должны проявляться в другом. Это означает, что иерархические структуры в слабой метрики порождают фрактальные структуры в пространстве действительных чисел. И обратно, если мы видим фрактальную структуру, то ей соответствует р-адичная структура в слабой метрике. Возможно, что именно поэтому мозг фрактален, иначе бы не было соответствия с пространством мышления. Как следствие, если мы видим природную фрактальную структуру, например, у дерева, то ей может соответствовать определенная структура в слабой метрике, отвечающая процессу мышления этого явления.
ВРЕМЯ Время необычная категория. Вот, что об этом феномене писал
«…Аристотель причисляет и время к количествам, у которых части не имеют определенного положения по отношению друг к другу. Однако мы не в состоянии предложить математическую модель, которая была бы адекватна аристотелевскому времени. Аристотелевское время является «монстром» с точки зрения математики. С одной стороны, время является непрерывным (как и все физические объекты). Но, с другой стороны, оно неупорядочено. В каком-то смысле аристотелевское время — это гибрид физического и духовного, что само по себе выглядит весьма привлекательно. Однако непрерывный в смысле Аристотеля континуум — вещественная прямая — является упорядоченным. А неупорядоченные р-адические деревья не являются непрерывными в смысле Аристотеля, так как они вполне несвязны. Таким образом, вопрос о выборе адекватной математической структуры для описания аристотелевского времени остается открытым. Кандидатом на роль аристотелевского времени может быть, например, двумерное время, описываемое вещественной плоскостью» [11, с.19] Одной из фундаментальных особенностей р-адических динамических моделей является дискретность времени.
В работе «Тринитарные заметки на полях. Часть 5» [18] я писал:
«Движение – это неопределенность, которая рождается в результате взаимодействия ε и D – объектов, описываемых через бесконечно малое и бесконечно большое гипердействительные числа. Каждый из этих объектов, как и пространство движения, возникли одномоментно с Субстанцией Отображения…. Движение там, где возникает фрактальность, как результат бесконечного взаимоотражения или самоотражения. Движение там, где самоизмерение идет непрерывно, что соответствует наблюдаемому нами золотому отношению.»
В этом смысле момент времени, как длительности, – это момент фиксации (актуализации возможности) конфигурации р-адического и вещественного мира в слабой метрики, что эквивалентно наблюдению.
В своей работе «Неархимедов анализ и его приложения» [19] А.Ю. Хренников вводит два процесса измерения: один процесс с убыванием единицы в m раз – появляются действительные числа, второй процесс измерения с возрастанием единицы в m раз – появляются m-адические числа. В дециметровой шкале измерения мы не можем получить точные значения для √3 и 1/3, а только их приближение. Поэтому √3 и 1/3 – только символы, используемые для обозначения бесконечных алгоритмов измерений.
То же верно и для m-адических измерений. Например, в 2-адической шкале
1/3 = 1+2+23+25 … =....1010112+
Если алгоритм с возрастанием единицы в m раз бесконечен, то появляются новые свойства бесконечно больших сумм, а именно: конечную относительно действительной метрики сумму можно представить в виде бесконечно большой суммы в m-адическом процессе измерений.
Интересные следствия для космологии.
В ней возможно перемещение на расстояние, равное 1/3 длины 1 за бесконечное число шагов единичной длины.
1/3 = 1+2+23+25 …
То есть подсчитывая бесконечное число временных интервалов Δt=1 для начального момента t0=0 мы возвращаемся к моменту t=1/3. Таким образом в рассматриваемой m-адической модели исчезает отношение порядка в пространстве-времени на космологической шкале, а пространство-время имеет неархимедову структуру.
Более того, для m=2 получаем
-1 = 1+2+22+23+24 +… +2n+…
Следовательно, в этой модели разница между направлениями в пространстве, так же как между прошлым и будущим, исчезает. Можно, суммируя бесконечное число интервалов Δt=1, вернутся назад на один временной интервал.
В m-адической модели космологическое пространство-время имеет структуру дискретного тора бесконечного радиуса. За космологическое время
Т = 0= 1 +(1+2+22+23+24 +… +2n+…)
m-адическая Вселенная в своем развитии возвращается к начальному моменту t0=0.
Так же для этой модели свойственно, что сингулярность плотности массы приводит к нулевой плотности, а бесконечное возрастание в силе гравитации или электромагнитном поле – к ее исчезновению.
Есть еще много необычных следствий, возникающих при использовании р-адического анализа к различным процессам. С ними можно ознакомиться в ряде работ, приведенных в приложении.
1. В.Ю. Татур, Биосфера и биолокационный эффект, «Ноосфера и Человек», М., 1990, с.90
2. В.Ю. Татур, Структура закона развития. Эволюция и ноосфера, Клаузура ноосферы, ч.1, с.279
3. В.Ю. Татур, С.В. Костюченко, Обоснование общечеловеческой этики и ноосфера, Клаузура ноосферы, ч.1, с.272
4. В.Ю. Татур, Тайны нового мышления, Москва, 1990.
5. В.С. Владимирова, И.В. Волович, Суперанализ, Дифференциальное исчисление, ТМФ, 1984, т.59, №1, с.3-27
6. В.С. Владимирова, И.В. Волович, Суперанализ, Интегральное исчисление, ТМФ, 1984, т.60, №2, с.169-198
7. В.С. Владимирова, И.В. Волович, Р-адическая квантовая механика, Доклады АН СССР, Физика, 1988, т.302, №2, с.320-322.
8. Hensel, Kurt (1897). «Ьber eine neue Begrьndung der Theorie der algebraischen Zahlen». Jahresbericht der Deutschen Mathematiker-Vereinigung 6 (3): 83–88.
9. Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
10.Боревич З. И., Шафаревич И. Р. Теория чисел, 1985, с. 25—28.
11.А.Ю. Хренников, Моделирование процессов мышления в р-адических системах координат, М.,2013
12. Pitranen М., TGD inspired theory of consciousness with applications to biosystems. Electronic book, 1998
13. Паршин А.Н. Размышления над теоремой Геделя // ИМИ, 2000. Вып. 5 (40).
14. Паршин А.Н. Идеальные числа Платона // С сайта bfrz.ru, 5.04.2006.
15. Ю.И. Манин, Математика как метафора, М: МЦНМО, 2008.
16. Улам С. Нерешённые математические задачи. – М.: Наука, 1964.
17. Augenstein B. Links Between Set Theory and Physics// Chaos, Solitons and Fractals. V.7. N 11, 1996. P.1761-1798.
18.В.Ю. Татур, Тринитарные заметки на полях. Часть 5 // «Академия Тринитаризма», М., Эл № 77-6567, публ.22919, 07.01.2017
19. А.Ю. Хренников, Неархимедов анализ и его приложения, М., 2003
Приложение
А.Ю. Хренников, Неархимедов анализ и его приложения
(http://www.trinitas.ru/rus/doc/0001/005b/00011764.htm)
А.Ю. Хренников, Моделирование процессов мышления в р-адических системах координат
(http://www.trinitas.ru/rus/doc/0001/005b/00011780.htm)
И.В. Данилевский, Квантово-Р-адическая онтология разума и закон Ципфа-Парето
(http://www.trinitas.ru/rus/doc/0016/001e/00163189.htm)
С.В. Козырев, р-адическая математическая физика: основные идеи, применения
(http://www.trinitas.ru/rus/doc/0016/001e/00163221.htm
С.Б. Каток, р-адический анализ в сравнении с вещественным, М., 2004
Полный текст доступен в формате PDF (6910Кб) ![]()
В.С. Анишин, Введение в прикладной р-адический анализ
Полный текст доступен в формате PDF (208Кб) ![]()
Ю.И. Манин, Математика как метафора, М., 2008
Полный текст доступен в формате PDF (2804Кб) ![]()
И.В. Волович, С.В. Козырев, р-адическая математическая физика, 2008
Полный текст доступен в формате PDF (512Кб) ![]()
В.Ю. Татур, Р-адические числа, ультраметрика и ментально-вещественный мир // «Академия Тринитаризма», М.,
|
|